基于小波变换的自适应电网谐波检测方法研究

许 丹 黄晓明 李献伟 楼柏良 黄弘扬



基于小波变换的自适应电网谐波检测方法研究

许 丹1黄晓明2李献伟1楼柏良2黄弘扬2

（1. 许继集团有限公司，河南许昌 461000; 2. 国网浙江省电力公司电力科学研究院，杭州 310014）

针对目前基波检测时存在的由于小波分解层数确定不当引起的频率混叠现象以及分析时运算量大造成的检测速度慢、实时性不高等问题，提出了一种基于基波和谐波频率确定分解层数的检测方法。该方法通过基波频率和最低次谐波频率确定最低频段边界，使基波与谐波有效隔离开，有效地减小了运算量，提高了基波特征信息的检测精度。

电能质量；基波；谐波；频率混叠；小波变换

近年来，随着电力电子技术的快速发展以及电网中非线性负荷的日益增多，配电网中谐波污染问题越来越严重，给电力系统和重要电力用户带来了不利影响。一方面，谐波影响各类电气设备、测量装置以及电能计量装置的正常工作；另一方面，电力系统阻抗在特定频率下会与并联补偿电容器发生谐振，使谐波电流放大，对系统和电容器组造成严重影响[1-3]。此外，谐波会加重电力系统中元器件的附加损耗，导致系统从发电、输电到用电的整个过程效率下降。

目前，使用电力滤波装置吸收谐波源产生的谐波是应用最广泛最有效的谐波抑制方法。而谐波检测是进行谐波治理的基础，直接影响到电力滤波装置的谐波治理效果。当前常用的谐波检测方法主要有：无源滤波、傅里叶变换、坐标变换以及小波变换等。无源滤波器的中心频率对元件参数十分敏感，受外界影响较大，难以获得理想的幅频特性。傅里叶变换存在着频谱泄露和栅栏效应，降低了测量精度。基于瞬时无功功率的坐标变换多应用于三相三线制电路的谐波检测，单相电路的检测算法复杂且不易实现。小波变换在时域和频域都具有较好的局部化特性，具有多分辨分析的特点，不仅应用于稳态信号检测，也适用于暂态信号检测[4-7]。基于小波分析的良好特性，使其在电力系统暂态检测、谐波测量等方面具有广阔的应用前景[8-10]。小波变换分解层数的确定是精确提取基波特征信息的关键，分解层数过大或过小均会对基波信息提取产生不利影 响[11]，但目前关于分解层数的确定尚没有统一的方法。本文研究了采样频率与小波变换分析基波提取精度的影响，提出了一种自适应确定小波分解层数的方法，并通过Matlab仿真验证了检测方法的可 行性。

1 小波变换与多分辨分析

1.1 提取原理

对任意信号()∈2()和小波基函数()，其关于小波函数ab()的小波变换定义为[12-13]

式中，为尺度因子，表征信号在频域上的伸缩；为平移因子，表征信号在时域上的平移。一般情况下，把尺度伸缩因子和连续平移因子的离散公式分别取作=，=0，其中，∈Z，0＞1。对应离散小波()可以表示为

（2）

多分辨分析是将原始信号按照频带不同分解成子带信号，并对每个子带信号各自做离散小波变换，从而获得不同的频率和分辨率[14]。图1所示为尺度为3的信号分解示意图，分解后信号可表示为S=A3+D3+D2+D1，其中A1、A2、A3是信号的低频部分，D1、D2、D3是信号的高频部分。利用小波分析对电网信号基波和谐波信息的提取过程如 下[15]：首先对信号进行多分辨率分解，得到基波和谐波分量在各尺度空间上的系数；然后根据基波在相应尺度空间的分解系数，重构出基波信号和谐波信号，从而实现对基波特征信息的提取，进而获取信号中的谐波信息。

图1 尺度为3的信号小波分解示意图

1.2 基函数选择

小波函数的选取不同，提取信息精度的结果就不同。对于小波函数的选择，一般考虑正交性、紧支性、正则性和消失矩等几个特征。①正交性保证了小波变换之间不存在关联，消除了信息的冗余度；②紧支性表征了小波的能量集中程度与局部化特性；③正则性代表小波的光滑度与分辨率；④消失矩描述了小波函数逼近信号的收敛率。考虑电网信号的特点，本文以具有正交性、紧支性、正则性和消失矩特性的Harr小波、db小波、sym小波以及coif小波4种常用离散小波为基函数对电网信号进行提取，其中以电网信号基波频率为50Hz，含有5次谐波和7次谐波为例，采样频率设为1000Hz进行分析，仿真结果如图2所示。

（a）重构波形

（b）误差分析

图2 不同小波基波的电网信号提取结果

从仿真结果中可以看出，除db小波外，其他小波在基波特征信息重构过程中均出现了不同程度的波形畸变，其中Harr小波提取的基波信息波形畸变程度最大。此外，db小波重构误差最小，sym小波和coif小波的重构误差分别为10%和20%左右，Harr小波重构后的失真度最大。可见，db小波函数非常适用于呈现周期特性的电网信号的分析提取。因此，本文以db小波作为电网基波检测的小波基函数。

2 自适应基波提取方法

2.1 采样频率与提取精度影响

分解层数直接影响小波分析结果的精度，当分解层数过小时，在通带中会引入不需要的频率波形，引起混叠现象，造成分析误差；分解层数过大，会引起多余的频带划分，算法进一步复杂，造成时间上的滞后性。小波变换方法是采用逐层下行二分的方法对频带进行划分（如图1所示），分解层数、采样频率和最低段频率边界满足以下关系式：

式中，为分解层数；s为采样频率；T为最低段频率边界。

由式（3）可以看到，采样频率是影响小波分析分解层数确定的关键环节：①采样频率应满足奈奎斯特定律，即采样频率大于信号最高频率的两倍，才能保证获取信号不失真；②采样频率与分解层数、最低频段边界存在代数关系，特别是对最低频段边界有直接影响，关系到小波特征信息的提取精度。假设电网中存在如下信号

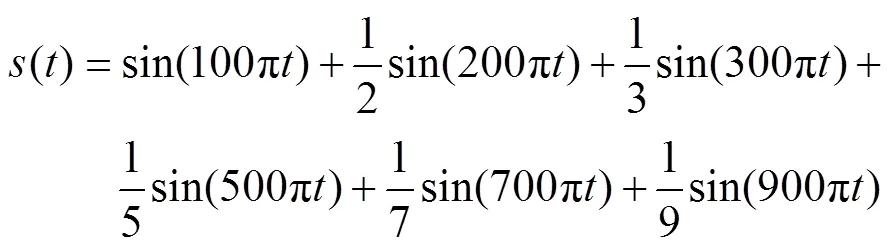
电压信号由50Hz基波以及2次谐波、3次谐波、5次谐波、7次谐波和9次谐波线性组合而成，根据奈奎斯特采样定理，采样频率应大于最高次谐波频率的两倍才能保证信号被完整采集，因此，本文研究了采样频率在950～1400Hz变化时，小波变换提取基波特征信息精度变化情况，其中，基波特征信息的提取精度通过误差率error来表示：

（5）

仿真结果如图3所示。当采样频率为950Hz时，基波提取误差较大，约为7%；随着采样频率的增加，基波提取误差逐渐变小，当采样频率为1220Hz时，误差率达到最小值，此时对应最低频段边界值为76.25Hz；随着采样频率的进一步增加，基波提取误差增大。

图3 不同采样频率对小波变换提取基波特征信息精度影响

上述现象与小波变换特性密切相关，基于多分辨分析的小波变换相当于对信号进行带通滤波[16]，其中心频率处的滤波效果最佳，而中心频率与采样频率呈正相关关系。小波变换的幅频特性如图4所示，当采样频率较小时，中心频率低于基波频率。随着采样频率的增加，中心频率逐渐向基波频率靠拢，此时具有最佳滤波效果和最优的基波特征信息提取精度。采样频率进一步增加，中心频率高于基波频率，滤波效果变差，此外，采样频率增加，通带变宽，可能会导致低次谐波通过，降低基波特征信息的提取精度。

图4 小波滤波幅频特性示意图

2.2 分解层数确定

提高基波提取精度的关键在于小波频段划分的最低频段只有基波频率，核心在于最低频段边界的确定。实际上，无论频段划分还是边界确定，都在于保证最低次谐波和基波有效的隔离开，而最低次谐波频率一旦确定，则分解层数和最佳采样频率也随之确定。为了确保最低频段仅含有基波频率，通过基波频率b和最低次谐波频率Hmin的均值来确定最低频段边界T，以达到基波特征信息的精确提取。

自适应电网基波方法检测流程如图5所示：①首先，通过快速傅里叶变换获得电网信号的频谱信息，包括电网的基波频率b以及最低次谐波频率Hmin和最高次谐波频率Hmax；②然后根据频谱信息确定最低频段边界T值，T=(b+Hmax)/2；③最后通过迭代分解层数，计算确定最佳采样频率s。

图5 自适应电网基波检测方法流程

以下将对稳态谐波信号、暂态谐波信号以及不同基波频率3种情况进行仿真，以验证自适应谐波检测法的可行性。

3 仿真分析

3.1 稳态谐波信号

电网的谐波源多为高频炉、炼钢炉、大型轧机、硅整流设备，其产生的谐波通常为稳态谐波。一般而言，配电网中的稳态谐波呈现以下特点[17]：①偶次谐波的含有率很少；②谐波次数越高，谐波含量越小。基于此，假设电网中存在如下信号：

首先对该信号进行快速傅里叶变换（FFT），以获得该信号的频谱信息，信号的频谱如图6所示。

从频谱图中可以看到，该信号除了含有50Hz基波信号外，还含有3次谐波和7次谐波。首先，根据基波频率和最低次谐波频率确定最低频段边界值T为100Hz，然后根据图5中所示关系迭代值，当等于2时，采样频率值为800Hz，大于最高次谐波频率的两倍，满足奈奎斯特定律。

为了验证检测方法的可行性，本文研究了在该情况下采样频率变化对基波特征信息提取精度的影响。其仿真结果如图7所示，随着采样频率的增加，基波特征信息提取误差总体上呈现先减小后增大的趋势，当采样频率为820Hz时，误差率达到最小，约为2.3×10-5。通过自适应检测法确定的最佳采样频率为800Hz，同样具有较高的提取精度，与采样频率为820Hz时的误差率相差不大。

（a）采样频率范围为500～1050Hz

（b）采样频率范围为700～850Hz

图7 不同采样频率对稳态电网信号基波特征信息提取精度的影响

3.2 暂态谐波信号

除了由大量非线性负荷引起的电力谐波外，含有电力电子器件的分布式电源受自然条件变化随机启停会在配电网中引入暂态谐波信号。暂态谐波往往呈现出频次高和随机性的特点，假设在电网中存在如下信号：

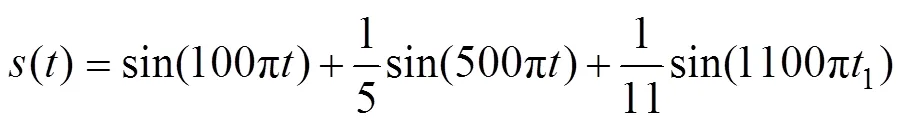
（7）

电压信号含有50Hz基波和5次谐波，并在0.5～1s内存在11次暂态谐波信号。首先对该信号进行FFT变换，其频谱图和小波分析结果分别如图8、图9所示。

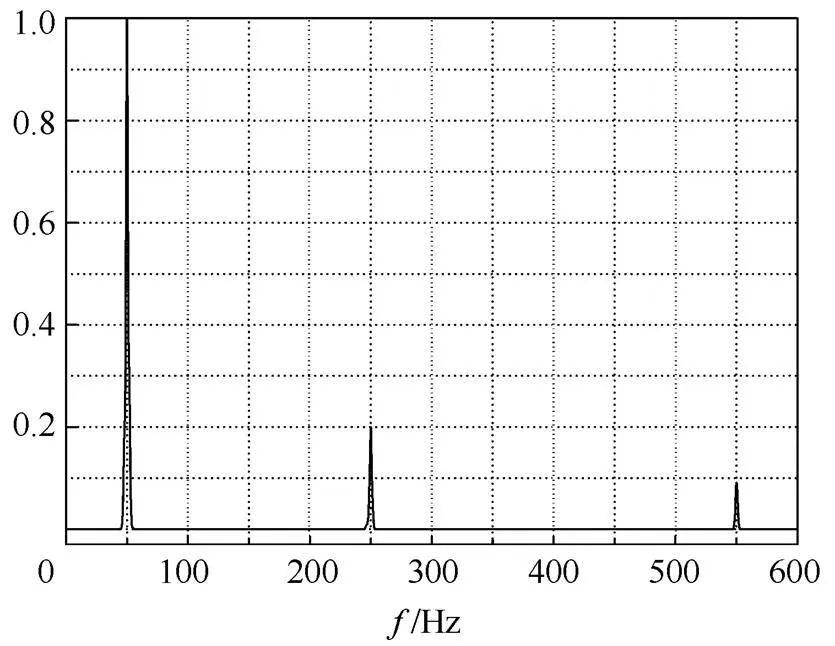
图8 暂态电网信号频谱图

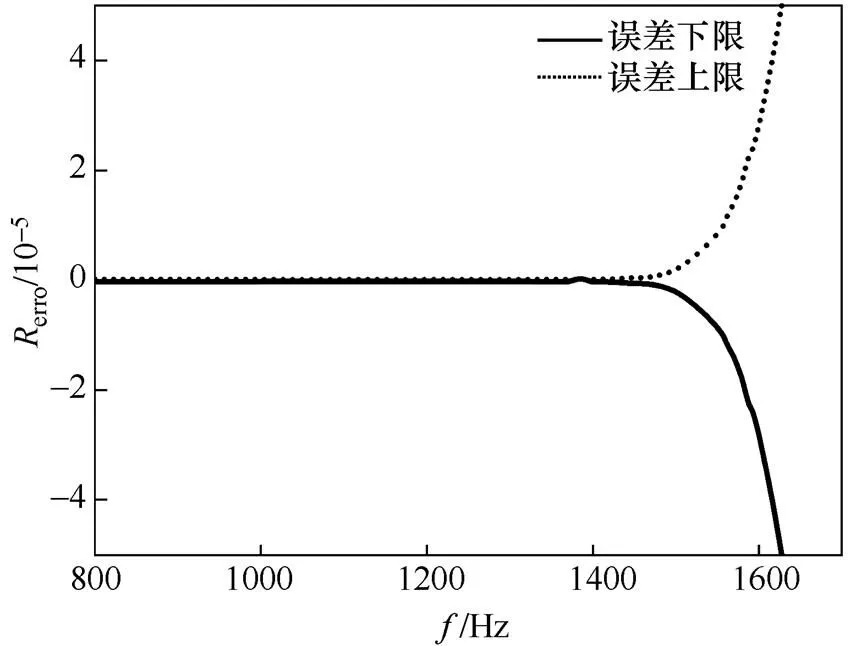
（a）采样频率范围800～1650Hz

（b）采样频率范围为800～1450Hz

图9 不同采样频率对暂态电网信号基波特征信息提取精度的影响

图8所示为电网信号的频谱信息，按照自适应检测法所述，确定最低频段边界T值为150Hz，分解层数为3，采样频率s为1200Hz。

图9所示为采样频率变化对基波特征信息提取精度的影响。其仿真结果如图10所示，随着采样频率增加，基波特征信息提取误差大体上呈现先减小后增大的趋势，并在采样频率为1180Hz时达到最小值，其值为1.65×10-5。而通过自适应检测法确定的采样频率为1200Hz，其基波特征信息提取误差约为1.67×10-5。可见对于暂态电网信号，采用自适应检测法与最佳条件下的基波提取信息精度相差不大。

3.5 不同基波频率的基波信息提取

在电网中除了谐波信号的变化外，基波频率往往存在着扰动。根据我国国家电能质量标准，基波频率偏差的允许值为±0.2Hz。假设在电网中存在如下信号：

电压信号由基波和2次谐波、3次谐波、7次谐波以及9次谐波线性组合而成，基波频率变化范围为49.8～50.2Hz。在不同基波频率条件下，其最佳采样频率下的误差与采用自适应方法基波提取法提取基波特征信息对比仿真如图10所示。

可以看到，随着基波频率的增加，基波特征信息的提取误差略有增大。当基波频率一定时，采用自适应方法提取出的基波特征信息精度接近于最佳条件下基波特征信息的提取精度。

4 结论

本文针对小波变换方法在电能质量检测中存在的分解层数模糊问题，研究了采样频率对基波特征信息提取精度的影响，提出了基于基波频率和最低次谐波频率确定分解层数的自适应检测方法，并在稳态谐波信号、暂态谐波信号和不同基波频率信号3种情况下进行仿真验证。仿真结果表明在不同情况下，自适应检测方法均有较低的提取误差，满足电能质量国家标准要求，并与最佳条件下的提取误差相差不大，对小波变换在电力系统谐波分析中的应用具有一定的参考意义。

[1] 翟晓君, 周波. 一种改进的插值FFT谐波分析算法[J]. 中国电机工程学报, 2016, 36(11): 2952-2958.

[2] 曹玲芝, 李振杰. 基于dq变换与小波多分辨分析的电力系统暂态复合扰动信号检测方法[J]. 电力系统保护与控制, 2016, 44(21): 138-143.

[3] 房国志, 杨超, 赵洪. 基于FFT和小波包变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2012, 40(5): 75-79.

[4] 田中大, 李树江, 王艳红, 等. 基于小波变换的风电场短期风速组合预测[J]. 电工技术学报, 2015, 30(9): 112-120.

[5] 范小龙, 谢维成, 蒋文波, 等. 一种平稳小波变换改进阈值函数的电能质量扰动信号去噪方法[J]. 电工技术学报, 2016, 31(14): 219-226.

[6] 朱红, 王勇, 马洲俊, 等. 基于小波神经网络的新型配电网单相电路选线算法试验研究[J]. 电气技术, 2016, 17(6): 81-85.

[7] 高倩, 陈晓英, 孙丽颖. 基于可调Q小波变换与基追踪的电能质量信号去噪[J]. 电气技术, 2016, 17(5): 49-53.

[8] 李秋燕, 黄永红, 陈万峰, 等. 基于小波变换的d-q电力谐波检测法研究[J]. 电测与仪表, 2015, 52(19): 24-29.

[9] 黄海宏, 江念涛, 毕楠夏, 等. 一种混合谐波检测法在APF中的应用[J]. 电力测量与仪器学报, 2016, 30(2): 297-303.

[10] 李正明, 徐敏, 潘天红, 等. 基于小波变换和HHT的分布式并网系统谐波检测方法[J]. 电力系统保护与控制, 2014, 42(4): 34-39.

[11] 李远军, 许钢, 林园胜, 等. 基于小波变换的电力系统谐波检测的研究[J]. 重庆工商大学学报, 2014, 31(6): 78-81.

[12] 赵惠玲, 周芸. 基于小波变换的电力系统谐波检测的研究[J]. 电子设计工程, 2012, 20(1): 77-80.

[13] 曾瑞江, 杨震斌, 柳慧超. 基于小波变换的电力系统谐波检测方法研究[J]. 电力系统保护与控制, 2012, 40(15): 35-39.

[14] 周龙华, 付青, 余世杰. 基于小波变换的谐波检测技术[J]. 电力系统及其自动化学报, 2010, 22(1): 80-85.

[15] 谷文静, 金涛. 基于小波变换的电力系统谐波分析研究[J]. 电气技术, 2012(8): 36-40.

[16] 房国志, 杨才山, 杨超. 基于Meyer小波和FFT的电网间谐波检测[J]. 电力系统保护与控制, 2011, 39(12): 90-93.

[17] 王肖芬, 徐科军. 基于小波变换的基波提取和频率测量[J]. 仪器仪表学报, 2015, 26(2): 146-151.

The Study of Self-adapt Harmonic Detection in Power Grid based on the Wavelet Transformation

Xu Dan1Huang Xiaoming2Li Xianwei1Lou Boliang2Huang Hongyang2

(1. XJ Group Corporation, Ltd, Xuchang, He’nan 461000; 2. State Grid Zhejiang Electric Power Company Electric Power Research Institute, Hangzhou 310014)

In view of the spectrum aliasing effect and the issues of slow detection and weak real-time performance caused by inappropriate wavelet level decision exist in the harmonic detection, a comprehensive harmonic detection method is proposed to fix the wavelet level based on the frequency of fundamental and harmonic wave. This method fixes the wavelet level by the fundamental frequency and the boundary of minimum frequency range, which separates the fundamental wave from signal accurately, resulting to the decrease of complicated computation and improvement of the detection precisionfundamental wave information.

power quality; fundamental wave; harmonic wave; spectrum aliasing effect; wavelet transform

许 丹（1990-），男，工程师，主要研究方向为配电网电能质量优化与治理。