不同加工方式影响的表面疲劳寿命研究

杨 杞



不同加工方式影响的表面疲劳寿命研究

杨 杞

（辽宁铁道职业技术学院，辽宁 锦州 121000）

离心压缩机是工业生产中重要的能量转化装置，针对其在实际生产中常常发生因叶轮疲劳破坏而导致的生产事故的问题，有必要对叶轮表面及内部损伤产生的疲劳裂纹进行研究，以确定叶轮的剩余寿命等具体的疲劳断裂性能。利用损伤力学的方法确立叶轮应力危险区域的裂纹萌生寿命模型并对萌生寿命公式进行推导，并考虑到叶轮加工表面粗糙度对叶轮应力以及裂纹萌生寿命的影响，对模型进行进一步的修正和完善，最终通过了Ansys软件的验证。结果发现模型公式推导出的裂纹萌生寿命与实际生产中叶轮的疲劳寿命相吻合，同时发现不同的加工方式对粗糙度以及叶轮的疲劳寿命的影响非常大，磨削加工叶片的疲劳寿命可以达到普通铣削加工叶片疲劳寿命的30倍以上。

表面裂纹；疲劳寿命；加工方式

离心压缩机是极为重要的能量转换装置，在国民经济中占有非常重要的地位，广泛应用于国民经济支柱产业以及国防军事工业等领域。近年来，随着压缩机大型化的变革式发展，叶轮的整体尺寸也随之变大，这些逐渐变大的叶轮损坏得越来越频繁，而大多数的损坏通常是由于叶片上产生裂纹导致的疲劳破坏[1-3]。

对叶轮表面及内部损伤产生的疲劳裂纹的研究分析应该以断裂力学及损伤力学为理论基础，这就涉及到了疲劳、断裂和材料三大学科。这种分析揭示表面裂纹的扩展规律；分析裂纹尖端附近的应力场-位移场和应力强度因子K等要素，以建立断裂准则；确定疲劳裂纹的临界阈值，也就是零件允许的裂纹长度；预测处于工作状态零件的剩余寿命等[4]。

19世纪中期，德国科学家Wohler设计了旋转弯曲疲劳实验机，进行了不同应力状态下的疲劳实验，并且首次提出了S-N曲线的概念，为疲劳寿命以及疲劳失效的研究提供理论基础。进入十九世纪后期，一些研究人员将平均应力在疲劳过程中的影响作为研究重点，通过疲劳实验将平均应力与疲劳极限以及疲劳寿命联系起来，提出了一些例如Gerber抛物线方程和Goodman等公式[5-6]。Neuber根据局部应力-应变法则进行疲劳寿命的预测，建立了Neuber方程。Miner根据研究结果提出了在变载荷作用下的疲劳损伤法则，即著名的Miner损伤累积理论。Manson和Coffin进行了很多疲劳实验，建立了Manson-Coffin公式。在之后的探索中，Wetzel以Manson-Coffin公式为理论基础，结合自己所开展的针对应力与应变之间的关系对疲劳寿命的影响，提出了局部应力-应变法。在宏观方面，Paris模型将应力强度因子幅值应用于裂纹扩展中，其中，应力强度因子又分为驱动力因子及阻抗力因子，从而提出著名的Paris公式，这一公式将裂纹长度随应力循环次数的变化情况表示为应力强度因子的函数，即

20世纪70年代，Kitagawa针对Paris公式中和的关系问题，经过大量实验后提出：

这表明在同一坐标下，不同状态下的裂纹的扩展速率曲线可以相交于一点。Jeglic提出关系式：

这一公式利用了激活能量0、表观激活能量和应力强度因子的幅值Δ间的关系[8]。

本文的研究工作通过利用Ansys 软件流体动力Fluent模块模拟叶轮在正常工况下的转速、气动等情况。通过软件的Crack裂纹模块在叶轮应力危险区域添加裂纹找到等效应力最大的区域，提取最大等效应力和对应的等效应变。利用损伤力学的方法建立裂纹萌生寿命的模型，运用最小二乘法拟合参数，获得完整的萌生寿命公式。代入提取的等效应力和等效应变值验证模型公式的合理性。同时，还将考虑到叶轮加工表面的粗糙度对裂纹疲劳寿命的影响。

1 离心压缩机叶片表面裂纹疲劳寿命模型

1.1 叶片表面疲劳寿命基础模型

本文将含损伤叶片的位移场当作具有相同载荷、相同约束、相同形状的无损伤叶片位移场的问题来求解。用、表示含损伤叶片的位移分量，U、V表示对应的无损伤叶片的位移分量。引用固体力学中有关位移和应变模态相似性的假设，即令=ζU,=ζV, 式中：是含损伤线弹性体的广义位移，为待定的系数。将其代入应变几何方程中：

再由损伤耦合效应的本构关系式。

(2)

式中：，分别为材料的杨氏弹性模量和泊松比。

利用虚功原理建立含损伤叶片的平衡方程。赋予广义的位移以虚功位移值得=uδζ,=vδζ，设含损伤叶片上作用的体力与面力分量分别为S，F与T，T，则外力的虚功可表示为：

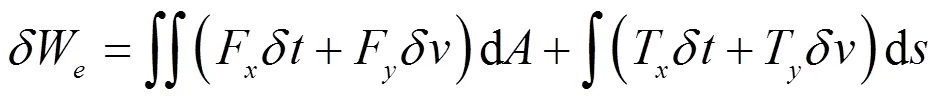
式中：，S分别为叶片的面积和静力边界。

同理可得内力的虚功表达式

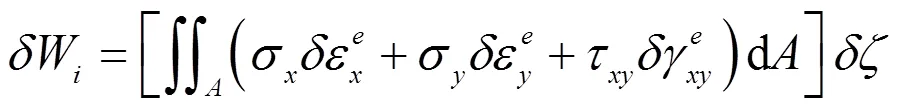
根据虚功原理

(5)

将内力虚攻和外力虚攻的表达式带入上式得

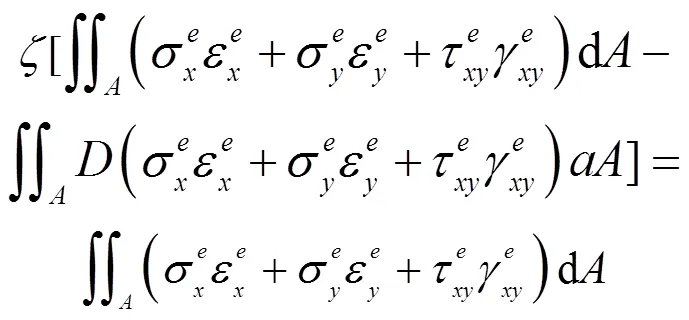
含损伤叶片内部任意点以及临界点的损伤演化速率方程:

和

式中：为叶片的循环次数；、D分别为叶片内部任意点以及临界点的损伤度；是叶片的材料常数，与循环特征相关；为叶片的材料常数，且>1；、ε分别为叶片内部任意点和临界点的等效应变

(8)

由叶片应变几何方程有=ζε，可得叶片内部临界点的损伤演化方程

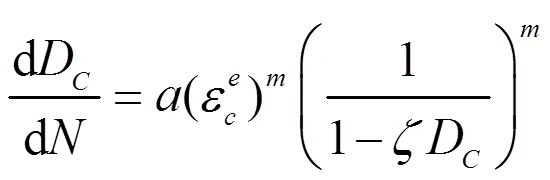
积分得

(10)

这里认为叶片无初始损伤，即当=0时，=D=0，且D的积分上下限为0和1。式中：N为形成裂纹时的循环次数，也就是所求的裂纹萌生寿命。

则式可表示为

(11)

即为预估N的叶片形成寿命的封闭解。应用该式即可得到预估叶片疲劳裂纹萌生寿命。

1.2 针对材料FV520B-I的疲劳寿命预测模型

应用预估叶片疲劳萌生寿命的封闭解答式，由式(11)有

(13)

用表示N,a，表示σ，则式(13)成为

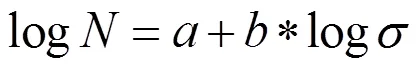
(15)

式(15)中的和，带入最小二乘法公式便可求解，再通过离心由压缩机叶轮的疲劳实验得到的疲劳性能实验数据，应用最小二乘法求得和，从而求得和的值

根据山东大学实测的离心压缩机叶轮材料FV520B-I超高周疲劳S-N曲线，从曲线中提取七组应力—循环次数的数据[9]：

、、、、、

将七组数据代入最小二乘法公式中，可以求得=-25.22779、=77.4，从而得

、

最终得到针对该离心压缩机叶轮叶片疲劳裂纹萌生寿命表达式：

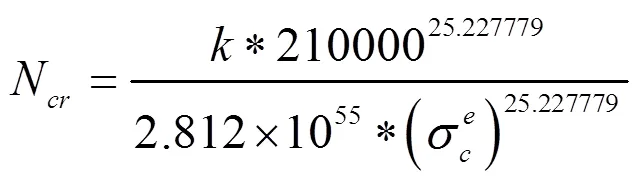
式中：

2 有限元分析

2.1 0.1 mm裂纹应力应变状态

以整体坐标系为基准，建立局部坐标系，修改局部坐标系的坐标值，调整其位置至正常工况条件下叶轮的最大应力区域即叶片前缘与叶轮顶盘的交接处；以调整好的局部坐标系为基准添加长度为0.1 mm的裂纹，设定裂纹的长半轴、短半轴及影响区域的值，添加叶轮转速15.43 r/min等约束条件，导入由Fluent模块分析的气动载荷等条件，利用Ansys软件计算叶轮的等效应力云图和等效应变云图。沿局部坐标系的X—Y平面切开裂纹，获得裂纹尖端的最大等效应力和相应的等效应变，如图1(a)和图1(b)。

提取裂纹长度为0.1 mm时裂纹尖端的最大等效应力0.1为716.02 MPa，相应的等效应变0.1为0.0035758 mm。

图1(a) 0.1 mm裂纹的最大等效应力

图1(b) 0.1 mm裂纹最大等效应力处的等效应变

2.2 0.2 mm裂纹应力应变状态

利用同样的局部坐标系，直接添加长度为0.2 mm的裂纹，设定裂纹的长半轴、短半轴及影响区域的值，获得裂纹尖端的最大等效应力和相应的等效应变，如图2(a)和图2(b)。

提取裂纹长度为0.2 mm时裂纹尖端的最大等效应力0.2为782.01 MPa，相应的等效应变0.2为0.0040141 mm。

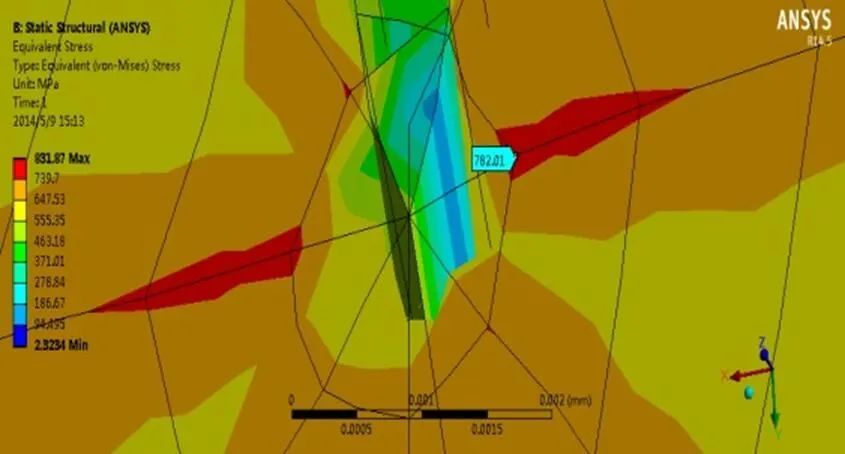
图2(a) 0.2 mm裂纹的最大等效应力

图2(b) 0.2 mm裂纹最大等效应力处的等效应变

2.3 0.3 mm裂纹应力应变状态

利用同样的局部坐标系，直接添加长度为0.3 mm的裂纹，设定裂纹的长半轴、短半轴及影响区域的值，获得裂纹尖端的最大等效应力和相应的等效应变，如图3(a)和图3(b)。提取裂纹长度为0.3 mm时裂纹尖端的最大等效应力0.3为806.59 MPa，相应的等效应变0.3为0.0041353 mm。

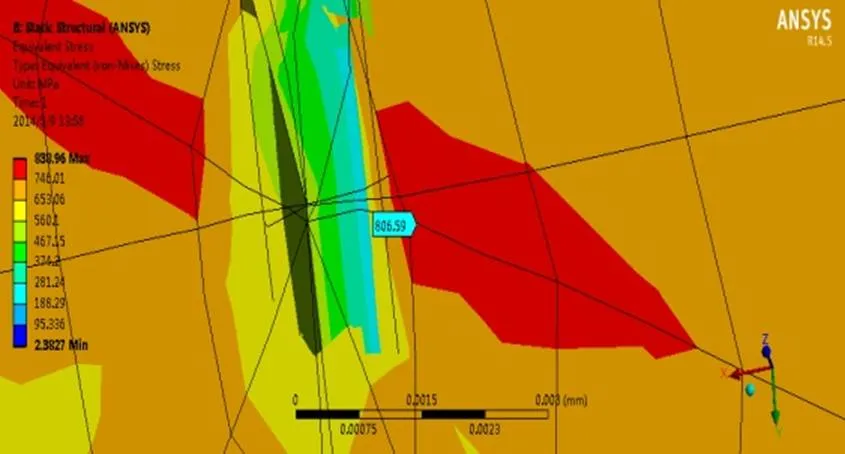
图3 (a) 0.3 mm裂纹的最大等效应力

图3 (b) 0.3 mm裂纹最大等效应力处的等效应变

2.4 不同尺寸裂纹的疲劳寿命

2.4.1 长度为0.1 mm裂纹的萌生寿命计算

已知0.1=716.02 MPa，无损伤初始临界应力σ=446.76 MPa，则临界点的损伤度:D0.1=0.3761 ，0.1=1.0992，0.1=0.03469 。从而，可得0.1 mm裂纹萌生寿命：。

2.4.2 长度为0.2 mm裂纹的萌生寿命计算

已知0.2=782.01 MPa，则临界点的损伤度:D0.2=0.37614287，0.2=1.0964，0.2=0.03478。从而，可得0.2 mm裂纹萌生寿命：。

2.4.3 长度为0.3 mm裂纹的萌生寿命计算

已知0.3=850.03 MPa，无损伤初始临界应力σ=446.76 MPa，则临界点的损伤度: D0.3=0.4450，0.3=1.0853，0.3=0.03513。从而可得0.3 mm裂纹萌生寿命：N0.3=3.2282×1010。

3 不同加工方法影响的表面疲劳寿命

叶片表面裂纹的萌生与扩展速率，以及压缩机叶轮的使用寿命，都受到叶片加工表面的质量的影响。表面粗糙度反映了叶片表面的几何形状误差，是衡量叶片表面质量的一个重要指标。Noll和Erickson分别比较了研磨、机加工、滚压和锻造这四种典型工艺下加工而成低碳合金钢表面的疲劳性能，结果发现在应力幅等于屈服强度的80%这种情况下，研磨加工表面的疲劳寿命是锻造加工表面疲劳寿命的20倍；Taylor和Clancy及Itoga通过对高强钢材的S-N特性曲线中表面粗糙度影响的研究，提出可以以断裂力学为基础通过两种不同的方式处理有关表面粗糙度的问题：加工表面较为粗糙的情况下可用短裂纹等效，而如果加工表面较为光滑，就要用小缺口来模拟[12-13]。Neuber把表面的加工纹理等效为无数微观的裂纹，从而将问题简化，并推导出表面应力集中系数K的经验公式：

式中：为裂纹的间距与裂纹深度的比值，但是实际生产过程中难以实现对已加工表面上值的测量，因而，值需要人为确定，本文中将的值确定为0.2；0为裂纹尖端的曲率半径，它并不是一个固定值，不同的裂纹对应的曲率半径区别很大。

3.1 铣削加工

铣削加工平面的粗糙度分别为4.324、4.128、4.369、4.724、4.278、4.011 μm 。粗糙度平均值为R=4.306 μm，代入式中计算可得：

考虑到应力集中系数，无损伤临界应力变为：σ=1.1856×446.76=529.68 MPa。因而，裂纹萌生寿命公式变为：

(19)

3.2 磨削加工

磨削加工平面的粗糙度分别为0.115、 0.171、 0.146、0.138、0.185、0.168、0.151、0.208 μm。粗糙度平均值为：R=0.1344 μm代入式中，计算可得：

考虑到应力集中系数，无损伤临界应力变为：σ=1.0328×446.76=461.41 MPa，因而，裂纹萌生寿命公式变为：

(21)

将以上计算结果汇总至表1。

由上面的计算结果可以看出，铣削和磨削两种不同的加工方式使加工平面的粗糙度有差别，从而在很大程度上影响了叶片疲劳裂纹的萌生寿命。为了探究裂纹的萌生寿命随表面粗糙度的变化趋势，本文以0.1 mm裂纹的情况为例，运用MATLAB软件计算出表面粗糙度在0.1 μm 至5 μm范围内变化时，疲劳裂纹萌生寿命的变化情况如图4。

图4 0.1 mm裂纹的萌生寿命随叶片表面粗糙度的变化

由上图可以看出，随着叶片表面粗糙度的增大，叶轮的循环次数不断减少，且当粗糙度小于1 μm 时循环次数减少得很剧烈，而当粗糙度大于1 μm 时，叶轮循环次数的变化越来越小。

4 结论

（1）利用损伤力学方法确立叶轮应力危险区域的裂纹萌生寿命模型并对萌生寿命公式进行了推导，根据实验数据确定了叶轮材料参数，同时考虑到了叶轮加工表面粗糙度对叶轮应力以及裂纹萌生寿命的影响，对模型进行了进一步的修正和完善。通过Ansys软件的Crack裂纹模块对叶轮表面裂纹萌生寿命模型进行了验证，结果证明根据本文模型公式推导出的裂纹萌生寿命与实际生产中叶轮的疲劳寿命相吻合，因而可以运用于叶轮裂纹萌生寿命的预测。

（2）由叶轮表面粗糙度影响的疲劳裂纹萌生寿命公式可以看出，初始裂纹的形成是一个缓慢的过程，然而一旦有裂纹形成，裂纹的扩展速度相当快，裂纹形成后每扩展0.1 mm所用的时间不足0.1 mm裂纹萌生时间的1%。这说明，叶轮上一旦出现可以检测到的裂纹（目前可检测裂纹长度为0.7 mm），应该立即准备停止叶轮的正常运行，进行再制造或者直接更换新叶轮。

（3）采用实验的方法，用铣削和磨削这两种不同的加工方式加工试件表面，以确定两种加工方式对加工表面的粗糙度以及叶轮疲劳寿命的影响。从计算结果得出，不同的加工方式对对粗糙度以及叶轮的疲劳寿命的影响非常大，磨削加工叶片的疲劳寿命可以达到普通铣削加工叶片疲劳寿命的30倍以上。由此得到对叶片表面进行精加工以降低粗糙度是提升叶轮使用寿命的关键手段。

[1] 吴君良. 基于断裂力学的离心压缩机叶片疲劳寿命研究[D]. 大连: 大连理工大学, 2012.

[2] 张小丽, 陈雪峰, 李兵, 等. 机械重大装备寿命预测综述[J]. 机械工程学报, 2011, 47(11): 100-116.

[3] 韩宇. 大型风力机叶片疲劳寿命分析[D]. 北京: 华北电力大学, 2011.

[4] Mohanty J R, Verma B B, Ray P K. Prediction of fatigue crack growth and residual life using an exponential model Part I (constant amplitude loading)[J]. International Journal of Fatigue, 2009, 31: 418-424.

[5] 雷冬. 疲劳寿命预测若干方法的研究[D]. 合肥: 中国科学技术大学, 2006.

[6] 李莉. 机械零件疲劳强度若干问题的研究[D]. 沈阳: 东北大学, 2009.

[7] Gerbe H. Bestimmung der zulassigen Spannungen in Eisen-konstruetionen[J]. Zeitsehritfdes Bayerisehen Arehiteekten und Ingenieur-Vereins 6, 1874: 101-110.

[8] 谭文峰. 损伤力学方法预估构件的疲劳裂纹形成寿命[D]. 秦皇岛: 燕山大学, 2009.

[9] Zhang Min, Wang Weiqiang, Wang Pengfeia, etc. Fatigue behavior and mechanism of FV520B-I in ultrahigh cycle regime[C]. 20th European Conference on Fracture (ECF20), 2014: 2035-2041.

[10] 章刚, 刘军, 刘永寿, 等. 表面粗糙度对表面应力集中系数和疲劳寿命的影响分析[J]. 机械强度, 2010, 32(1): 110-115.

[11] 肖维灵, 陈海波, 殷琰. 表面粗糙度对Glidcop和Q345低周疲劳寿命影响的试验研究[R]. 合肥: 中国科学技术大学, 2014.

责任编校：刘亚兵

Study of Surface Fatigue Life Influenced by Different Manufacturing Methods

YANG Qi

（Liaoning Railway Vocational and Technical College, Jinzhou 121000, China）

Centrifugal compressor is an important energy conversion device in the industrial production. While in actual production, fatigue damage of the impeller always causes production accidents. So we must analyze fatigue cracks in and on the impeller to determine the impeller’s performance of fatigue fracture such as residual life, so as to avoid the production accidents. In this paper, the crack initiation life model and the initiation life formula of the impeller’s dangerous zone are established by using the method of damage mechanics. The material parameters of the impeller is determined according to the experimental data, at the same time considering the surface roughness of the impeller’s influence on the machining stress and crack initiation life, the model is further improved and revised and finally the Ansys software is verified. It is found that the crack initiation life deduced by the model formula coincides with the fatigue life of the impeller in actual production, and different manufacturing methods lead to different roughness and fatigue life of the impeller, and the fatigue life of the blade can reach more than 30 times of the fatigue life of ordinary milling blades.

surface crack; fatigue life; manufacturing method

10.15916/j.issn1674-3261.2017.04.012

TH452

A

1674-3261(2017)04-0262-06

2016-12-09

杨杞(1982-)，男，辽宁锦州人，讲师，硕士。