M方纠缠态应用于时钟同步的策略研究

赵 颖，杨海英，夏涤尘



方纠缠态应用于时钟同步的策略研究

赵 颖1，杨海英1，夏涤尘2

（1.辽宁工业大学计算中心，辽宁锦州 121001；2.锦州市现代服务学校，辽宁锦州 121001）

将最大限度方纠缠态应用于多方时钟同步。研究结果表明，量子系统中时间信息编码有2种方法，第一种方法是基于光子到达次数的相关性，或者通过零差检测光信号到达的次数；第二种方法则是基于量子系统内部的时间演化。采用局部不同分组的分解变化来生成本征态集体能量最大纠缠，应用时钟平均时间来决定本时钟调整数度，纠缠的效率通过各方的有效合作和分享测量信息而得到。

多方纠缠态；二分纠缠态；时钟同步

量子时钟同步是基于量子物理的新型技术，在导航、定位、通信等方面都有重要的应用，其核心地位不容忽视。然而当前传统时钟同步理论在诸多方面无法满足实际需求，同时对应用于卫星导航方面的时钟同步在修改发生误差方面也存在许多难点问题，所以随着量子技术的迅速发展，将量子技术应用于时钟同步协议自然成为研究的新课题。其中量子时钟同步协议是量子信息领域的基础[1]，它详细说明了量子系统中时间信息编码的2种方法。第一种方法是基于光子到达次数的相关性，或者通过零差检测光信号到达的次数[2-5]。第二种方法则是基于量子系统内部的时间演化[6-9]。

量子时钟同步协议最初能够有效地应用于量子时钟同步，即通过增强双方二分纠缠态时间差灵敏大小的测量值而实现的。有学者把这个想法扩展到多方量子时钟同步协议[9]中，引入一个纠缠态，即中央时钟和其他各时钟之间的二分纠缠态。但是，这个态所代表的二分纠缠态会随着时钟数量的增加而迅速减小。因此，专家指出，这是态的一个衰减问题，这个问题可以通过使用与其相反的态得到解决并进行了实验论证。该协议中有一半的比特设为0，另一半设为1。在多方纠缠态问题中还需要了解对所有地点进行观测的测量结果。本文所探讨的问题是如何构建一个最大限度多方纠缠态协议来有效解决量子系统中时钟同步问题。

1 基础理论及状态概述

1.1 基础理论

(1)1，2，3粒子纠缠态

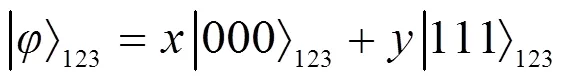
其中，是复系数并满足归一化条件：││2+││2=1，││2+││2=1，││≥││如果发送者Alice想要三粒子未知的纠缠态发送给接受者Bob，如果Alice和Bob搭建最大纠缠两粒子量子信道：

(2)

所以,想发送的粒子1，2，3与此纠缠态所形成的的总量子态，其中Alice拥有粒子1，2，3，，而Bob拥有。

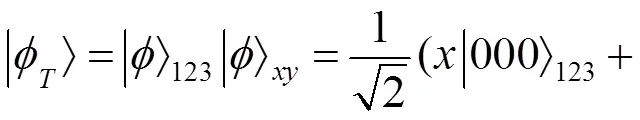
(3)

因为想成功完成量子态的隐形发送，首先发送者对粒子(1,)进行Bell基测试，Bell基为：

(5)

通过测试，总量子态会出现以下可能情况：

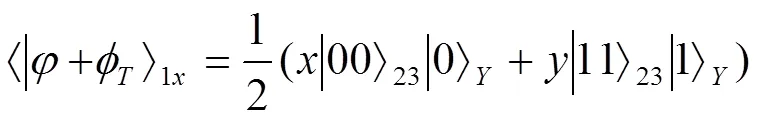
(7)

(8)

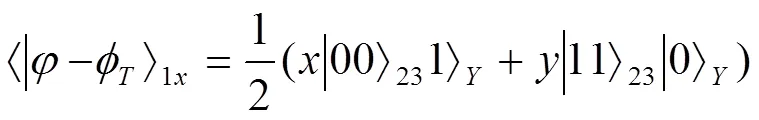
发送方完成测试后，通知Bob，Bob根据原始信息，对手里粒子执行相应的幺正操作1,其中粒子2，3和所处的量子态变为：

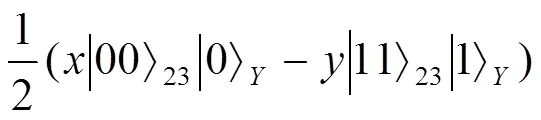
(2)递推至粒子纠缠态

当要传送的粒子是粒子纠缠态时，可以最后得到:，Bob引入-1个辅助粒子1,2…y-1，初态处于，然后操作Bob手中的和辅助粒子t(=1,2,…,-1),其中粒子是控制位，辅助粒子t(=1,2,…,-1),为靶位，经过控制非门的操控，粒子和辅助粒子t(t=1,2,…,-1),组成的量子系统为:

1.2 状态概述

随着现代时钟同步技术的进步，时钟校对精度技术也是重要的研究方面。基于附加税学的基础理论，通常采用爱丁慢协议和爱因斯坦协议。近几年人们利用量子强心剂的特点研究时钟同步测量技术，量子相关基础函数作为时钟同步测量的依据提出实验的基础。而时钟同步问题是多方纠缠态的能量本征态问题，是当所有量子处在相同的能量基础状态时其总的能量极值，本征态不是简单的2个能量极值本征态的叠加。因此，在不改变多方纠缠态的情况下要想获得整体能量本征态，则局部能量本征态的一半应该通过局部适当的统一翻转变化得到。在设置量子比特时，它的前一半是翻转得到，而后一部分是可翻转的，这样方纠缠态的能量本征态就可以通过对应的公式得到各自的局部能量本征态。现在研究的时钟同步协议是把纠缠的量子比特分配给各方本地时钟，每个量子系统被描述为在一个固定频率上围绕轴进行的二能级自旋进。这样相干对时钟同步的影响达到最小。目前的研究主要集中在对量子时钟基本属性的考虑，这些观点在布泽克等人的工作中进行了介绍[5]。本文提出的协议假定各态配置好后，其内部自旋态的演变取决于时间的流逝，时钟同步问题被转化为不同时钟测量差异值的识别问题。

为了确保所有各方的时钟同步，把量子比特划分为2个组，每一方都有可能接收一个量子比特的翻转组，或者从翻转组收到一个量子比特。假设定义一个序列{f}用来描述每一个分布，其中，=1,…,。如果方时钟所有者的量子比特是一个量子比特的翻转组，那么f=0，否则，f=1。由于2种情况的数量是相等的，所以，分布序列{i}是通过二项式系数!/((/2)!(/2)!)给出。不同组的分工是通过每一次运行而随机决定的。

使用纠缠态的同步协议要求纠缠的量子比特各有分工，协同合作。双方协议的逻辑关联被应用到2组所有测量的信息中。因此，通过选择合适的分工，可以使GHZ的完整纠缠态去有效地同步各方时钟。本文介绍了这种协议，并评估了它的效率。与基于二分纠缠态时钟同步协议中获得的效率进行了对比，并将其应用于态中。

2 对比实验

量子技术基于量子物理特点，被用于时钟同步的研究，使得可以充分利用量子纠缠的特征进行对应的时钟同步实验。对于多方纠缠态时钟同步[13]是否优于多方纠缠态中以各二分纠缠态为单位进行的时钟同步还在探讨中。由于方时钟的并行同步也可以通过-1方时钟在相同时钟标准下同步分离而获得。所以，每一比特都受控于中央时钟的拥有者，在给定的时间内，中央时钟的拥有者测量-1方比特的值。是与纠缠一方的序号。同样，与中央时钟纠缠的各方也依照其本地时钟t对其值进行测量。中央时钟用其测量结果与各方测试值进行比较，时钟拥有者就可利用相应公式对其产品的期望值做出估算，并据此调整它的时钟精度。

完整的多方纠缠态同步协议如图1所示。这里有个空间分离的不同步时钟，其中1个是标准时钟，剩下-1个时钟都分别与标准时钟采用二分纠缠态的时钟同步及通信连接。中央时钟的拥有者必须分享与-1方彼此同步时2种量子比特状态下的每个测量值。

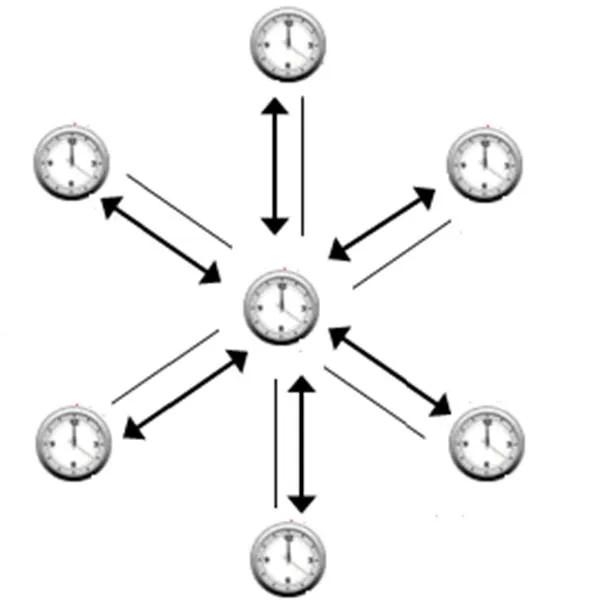
图1 利用纠缠态并行分布的时钟同步插图

本协议中的时间精度估算与使用多方纠缠态协议所得到的完全相同。然而，二分纠缠态的并行分布要求每一次测量的量子比特位2(-1)比特，而对应的多方纠缠态协议中只有比特。时钟同步的效率可以通过对每个调整时间i-的误差i进行估算。其中误差i是由测量值给出的，即i=1/(ω)。按照所需数量的量子要求，使用多方纠缠态能够通过纠缠的双方使效率增加。中央时钟拥有者提供多种参考量子给纠缠态各方，允许各方的参与者使用-1量子比特作为共同参考。

3 实验测试

量子物理规律决定量子时钟同步的同步精度，它突破了传统时钟同步的极限，当前采取的量子物理理论，原则上使同步精度可达皮秒极。

例如，参考时钟和拥有同样的频率，参考时钟与之间有一个时间差ΔT。同一时间产生的光子对抵达的时间是相同的，基础公式为：

设是时钟对理想时钟的偏差，则有：

(12)

设是时钟对理想时钟的偏差，则有：

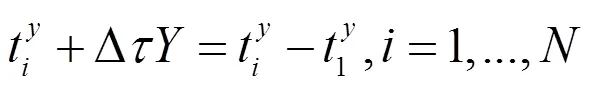
(14)

组合下面的函数：

为了将时钟同步到一个标准的时钟上，可以简单地改变时间的调整，从而改变各方的本地时间。为确保所有各方机会均等，标准时钟可以使用量子比特的随机分布，使每一个分布的量子比特翻转组或翻转组的量子比特都有同样的可能。跟踪不同分布，为其分配一个指标，使每个序列的元素根据相应公式计算。时间差异T的估算可以用一个精确的测量结果：

来统计，这里j是分布状态下接收和测量的次数。得到大量测量数据之后，各方都对所有可能的时间差异j有了估算。然而，每一个时间差异j对各方的影响是不同的。具体而言，各方都能通过或获得不同的差异。

利用测量值的相关性，可以获取时钟同步的最大限度多方纠缠态的所有功率，从而获取纠缠态的时间敏感度。所有各方都必须分享它们的测量结果和决定产品的所有结果。方合作，有效测量单个量子的干涉条纹，需要通过测量时间差异的翻转组量子比特或量子比特翻转组的次数来确定时间的敏感度。显而易见，最大限度多方纠缠态时钟同步取决于时钟同步访问中的测量结果。因此，需要各同步方之间实时有效的通信。将不同时钟进行状态配置之后，当本地时钟指向某个特定的时间点时，测量时间和量子比特的观察测量系数相关联。由于局部测量代表局部量子比特的最大时间敏感度，多方纠缠态的一致性只能由局部测量结果得到。即测量结果与时间紧密相关。在时间的观察测量值根据相应公式得到。测量结果的特征值是±1。测量结果相应的本征态是状态的平等叠加，相位取决于进行测量的时间。该测量值达到了局部量子比特的最大时间敏感度。

利用组态和的一致性给出能量本征态最大限度多方纠缠态的时间敏感度。这种一致性改变了集体测量结果的概率，集体测量结果受状态的影响。因此，多方纠缠态的时间敏感度可以用所有测量结果的期望值来表示。设各部分的实际测量时间是{1,2…t}，则这个期望值通过相应公式得到。

在同步协议的最后一步，同步时钟各方必须估算出各自的本地时钟与标准时钟之间的时间差异。定义标准时钟为所有的时钟同步的平均时间。图2给出了多方最大纠缠态的时钟同步图示。

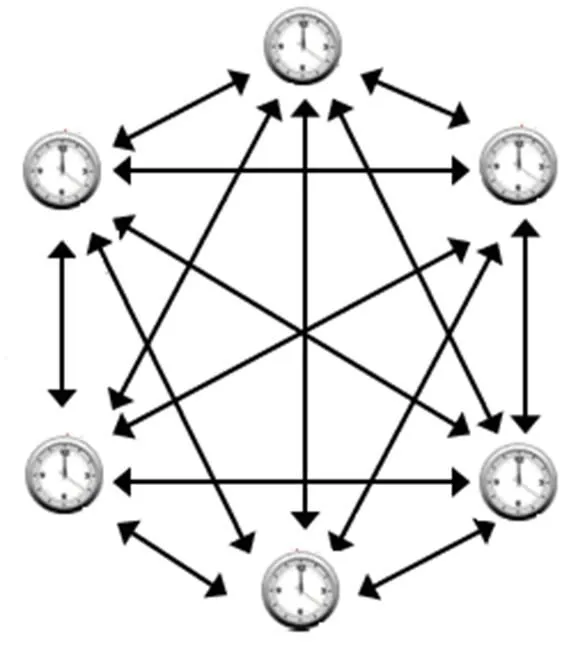
图2 最大纠缠态的时钟同步插图

4 实验评估

通过实验测试，将最大限度方纠缠应用于多方时钟同步，提出多方量子时钟同步协议，其中采用局部不同分组的分解变化来生成本征态集体能量最大纠缠，应用时钟平均时间来决定本时钟调整数度，纠缠的效率通过各方的有效合作和分享测量信息而得到。时钟同步中所需额外的参考量子比特由中央时钟的拥有者提供。在单一中央量子与其他-1方量子之间的同步使用二分纠缠态协议中的/(2(-1))2因子来获得灵敏度的衰减。在给定数量的量子比特情况下多方纠缠态协议能够达到时钟同步的精度要求。其中时间段是通过量子比特的动态共振频率定义。定义相对精度为对于多方纠缠态，量子比特的测量精度使用=比特，相对精度根据相应公式求出。这样，通过各方纠缠比特并行分布的二分协议执行时成功率为50%。即，量子比特的测量精度为=2(-1)比特，相对精度根据相应公式计算出结果。就方而言，其精度等于各部分比特之和，多方协议精度与各方比特呈线性比例/。

该方法在每次运行时把参与各方随机分为2组，根据所有时钟的平均时间来决定本地时钟的调整精度，进而分享本地时间的测量结果。二分纠缠态协议相比较最大限度纠缠态能够通过减少获得精度所需的比特数量改善时钟同步的性能，从而提高其同步的效率。而从实际的角度来看，要获得与所描述的情况接近的结果，局部量子比特的丢失和移相误差必须远远小于1/。相反，退相干的灵敏度也强调协议的合作特性：如果一方发送错误信息，时钟不会同步。时钟同步的精度与并行分布的-1个二分纠缠态协议中所获得的精度完全一致，但是使用的比特数量却减少了一半。最大限度多方纠缠态的效率能够通过参与同步各方的有效合作和分享测量信息而得到提高。提出了将GHZ态下的最大限度方纠缠态应用于多方时钟同步。

当然，多方纠缠态的使用也存在若干困难，因为一个量子比特的丢失就将完全毁坏多方纠缠态中相关量子比特的一致性。最大限度多方纠缠态时钟同步也强调协议中各方合作的特性。

[1] 王朋朋. 多方量子通信协议研究[D].张家界: 吉首大学, 2012.

[2] Bahder T B. Clock Synchronization and Navigation in the Vicinity of the Earth[J]. Physics, 2004, 55: 289-326.

[3] Valencia A, Scarcelli G a, Shih Y. Distant clock synchronization using Entangled Photon-pairs[J]. Applied Physics Letters, 2004, 85(13): 2655-2657.

[4] 蒋忠胜, 吕洪军, 解光军. 利用5粒子纠缠态实现四粒子w态量子信息的分离[J]. 量子电子学报, 2013, 30(3): 310-313.

[5] 周小清, 邬云文. 三光子纠缠W态隐形传输令牌总线网的保真度计算[J]. 光子学报, 2010, 39(11): 2093-2096.

[6] 周南润, 曾宾阳, 王立军, 等. 基于纠缠的选择自动重传量子同步通信协议[J]. 物理学报, 2010, 59(4): 2193-2199.

[7] 谢端, 彭进业, 赵健, 等. 基于MZ干涉仪结构的量子时钟同步方案理论研究[J]. 西北工业大学学报, 2011, 29(4): 614-618.

[8] Yurtsever U, Dowling J P. A Lorentz-invariance Look at Quantum Clock Synchronization Protocols Based on Distributed Entanglement[J]. Phys Rev A, 2002, 65: 052317.

[9] Jozsa R, Abrams D S, Dowling J P, et al. Quanturn Clock Synchronization based on Shared Prior Entanglement[J]. Phys Rev Lett, 2010, 85: 201-226.

责任编校：孙 林

Strategy Research on Application of-multipartite Entanglement Stateabout to Clock Synchronization

ZHAO Ying1, YANG Hai-ying1, XIA Di-chen2

（1.Computer Center, Liaoning University of Technology, Jinzhou 121001, China; 2.Jinzhou Modern Service School, Jinzhou 121001, China）

The maximum sensitivity on the local clock time is determined by the average time of all clocks. The result here shows how the full power of maximal multipartite entanglement can be used to improve the performance of clock synchronization if all parties involved cooperate to share their measurement information.

maximal multipartite entanglement; bipartite entangled states; clock synchronization

10.15916/j.issn1674-3261.2017.04.003

TP311

A

1674-3261(2017)04-0221-04

2017-03-09

辽宁省本科教学改革项目(2016300)

赵颖(1966-)，女，辽宁营口人，副教授。