双极值模糊软集运算的研究及应用

华逢彬，王艳平



双极值模糊软集运算的研究及应用

华逢彬，王艳平

（辽宁工业大学 理学院，辽宁 锦州 121001）

从参数集的信息角度将双极值软集与模糊集相结合，首先提出了双极值模糊软集的概念，然后定义了双极值模糊软集的交、并、补、且、或运算，并证明了其运算性质。最后基于双极值模糊软集给出一种决策算法，用来解决投资过程中基金选择的问题。

软集；双极值软集；双极值模糊集；双极值模糊软集

随着信息技术的快速发展，不确定性问题的研究变得日益复杂，单一的模糊集理论[1]、粗糙集理论[2]以及软集理论[3-4]都无法解决这些不确定性问题，因此几种理论的融合成为研究的热点。近年来许多专家学者将模糊集理论、直觉模糊集理论、区间值模糊集理论融合到软集理论当中，从而产生了模糊软集理论[5]、直觉模糊软集理论[6]、区间值模糊软集理论[7]、区间直觉模糊软集理论[8],并且成功应用到数据分析、数据挖掘、决策等领域。两极性是事物的固有属性，它的平衡在一切系统的正常运行中起到关键作用。在大数据时代，信息的两极性特点尤为突出，单一的模糊集理论在处理两极性的不确定信息时显得力不从心，因此在1994年Zhang[9]提出双极值模糊集理论。Lee[10-11]对双极值模糊集的概念进行了补充，从语义上对双极值模糊集进行了阐释。Abdullah等[12]及杨文华等[13]将双极值模糊集融合到软集理论中，提出了双极值模糊软集理论。Maji等[14]从参数集信息的角度定义了“非参数集”，即参数集的否定形式组成的集合，考虑参数集本身的特点，参数集与非参数集并不是完全对称的信息，参数集合中就存在灰色区域。为了能够更好地处理这样的问题，可以从参数集本身的信息特征出发，考虑事物的两极性。文献[15]将两极性理论融合到软集理论中，从参数集出发提出了双极值软集的概念，并定义了新的双极值软集运算。本文将这一思想推广到双极值模糊软集的构造，即从参数集本身的信息特征出发构造双极值模糊软集，从而给出不同于已有文献的新的双极值模糊软集，并定义了普通交、普通并、严格交、严格并、补集及“且”、“或”运算，讨论了它们的运算性质，最后给出一种基于双极值模糊软集的决策算法来解决投资过程中基金的选择问题。

1 预备知识

首先复习一下有关软集、双极值软集的基本知识。

定义1[3]设为初始论域，为参数集，且。称序对为上的一个软集，其中是到的幂集的一个映射，。上的一个软集就是的子集的属性族，对任意的，被认为是中的—近似元素组成的集合。

定义2[15]设为初始论域，为参数集，且。称三元组为论域上的双极值软集，其中、为映射：，，且满足，。

定义3[15]设和为上的两个双极值软集，如果满足(1)(2),，，则称为的双极值软子集，记为。

定义4[15]设和为上的两个双极值软集，如果且，则称和为双极值软相等，记为。

定义5[15]设为上的一个双极值软集，对于，，，则称为上的空双极值软集，记为。

定义6[15]设为上的一个双极值软集，对于，，，则称为上的满双极值软集，记为。

文献[13]中提出的扩展交、扩展并、严格交、严格并及“且”、“或”运算如下。

定义7[15]同一论域上的两个双极值软集和的扩展并定义为，其中，对于都有：

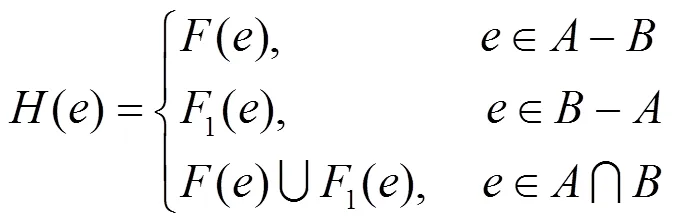
定义8[15]同一论域上的2个双极值软集和的扩展交定义为，其中，对于都有：

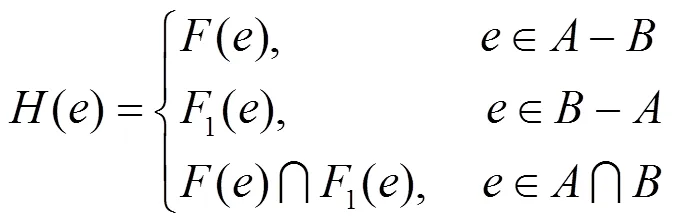
定义9[15]同一论域上的2个双极值软集和的严格并定义为，其中，对于，，,记为。

定义10[15]同一论域上的2个双极值软集和的严格交定义为，其中，对于，，，记为。

定义11[15]设和为上的2个双极值软集，则定义且为，其中，对于，，，记为。

定义12[15]设和为上的两个双极值软集，则定义或为，其中，对于，，，记为。

2 双极值模糊软集的运算及性质

下面把上述双极值软集的定义推广到模糊集，给出新的双极值模糊软集定义。

依据双极值软集的扩展交、扩展并以及严格交、严格并的运算，给出双极值模糊软集的扩展交、扩展并、严格交、严格并的运算如下。

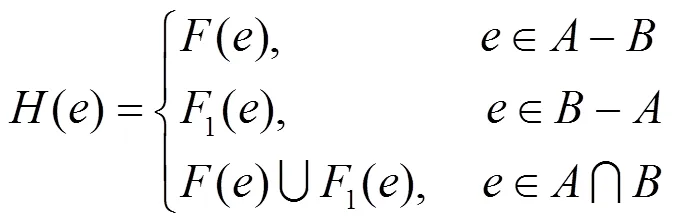
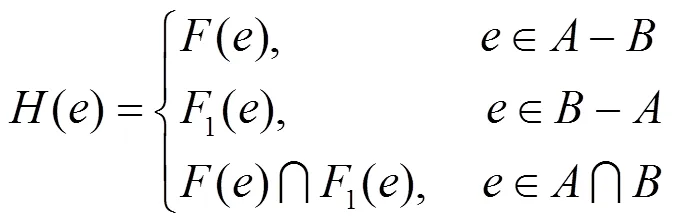
在文献[14]中引入表格的形式来简单地描述一个软集，本文利用这种形式来简洁地表示双极值模糊软集。

定义24 对于一个双极值模糊软集，可以简单地表示为：

，，，

，，，

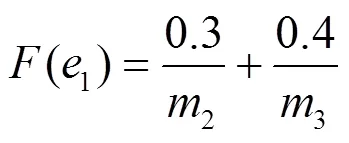
用表格的形式可以表示为表1和表2。

表1 双极值模糊软集(F,G,A)

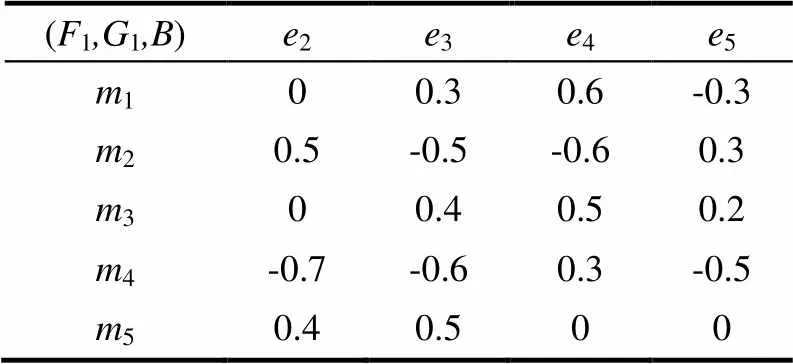
表2 双极值模糊软集(F1,G1,B)

,,

,,,,,

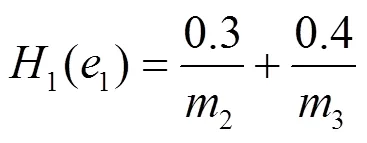
其他计算依定义可得。

从性质(7)、(8)中可知，扩展并与严格交满足包含关系，但是扩展交与严格并不满足包含关系。其余性质由定义直接可得或类似可证，下面就性质(9)给出证明。

3 双极值模糊软集在决策中的应用

在专业科学领域，专家应用专业知识做出精准的判断是决策过程中的一项重要因素。本文利用可用信息集合提出一个基于双极值模糊软集的决策算法来解决投资过程中最优基金选择的问题。

定义24[2]令为一族等价关系，，如果不可区分关系，则称为中不必要的；否则称为中必要的。中所有的必要关系组成的集合称为的核，记作。

下面定义一个算法来解决遇到的双极值模糊软集的决策问题。算法：

(4)依据决策属性值的大小重新对可以选择的对象从大到小的顺序进行排列，具有相同值的对象按照顺序排列。

(5)按照定义24计算参数集的核。

(6)如果核为参数集则执行下一步，若不为参数集则依据核的属性值重新计算的值并进行排序。

(7)找到决策属性值的最大值对应的选择对象，则该对象为最佳对象。

例2 随着现代社会经济的发展，投资基金越来越受到投资者的青睐，选择一个风险小、收益高的基金是所有投资者的向往。取为8支可供选择的基金，参数集合为基金的评价因素组成，表示为，其中~分别表示风险性小、收益性高、基金规模大、投资组合比较稳定、投资选择时机合适、基金经理投资水平高、基金费用低、流动性高、混合型投资基金。参数集的否定集合为，其中至分别表示安全性低、收益性低、基金规模小、投资组合不稳定、投资选择时机性差、基金经理投资水平低、基金费用高、流动性低、股票型投资基金。

下面按照所提供的算法来选择一支最佳的基金来进行投资。

(4)根据核的定义，依据表4可得：

表3 双极值模糊软集(F,G,A)

表4 双极值模糊软集(F,G,A)生成的属性表

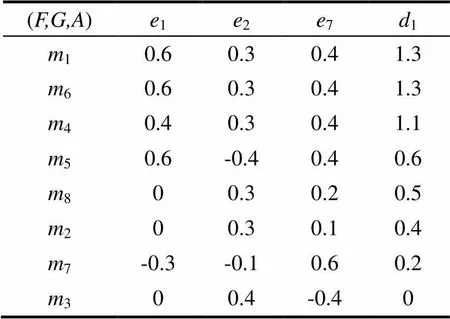
表5 双极值模糊软集(F,G,A)生成新的属性表

(6)可以得出结论：在可供选择的8支基金当中第1支与第6支是投资者进行投资的最优选择。

4 结束语

从参数集的角度将双极值软集与模糊集相结合，提出双极值模糊软集的概念，这是对软集进一步的推广。在新的定义下给出扩展交、扩展并、严格交、严格并、补集、且、或的运算以及运算性质，并证明了De Morgan律成立。最后针对金融行业的实际问题提出一种决策算法来解决投资过程中的基金选择的双极值模糊软集问题，从而为不确定性问题提供了一种决策方法。

[1] Zadeh L A. Fuzzy sets[J]. Information and Control, 1965, 8: 338-352.

[2] Pawlak Z. Rough sets[J]. International Journal of Computer Information Science, 1982, 5: 341-356.

[3] Molodtsov D. Soft set theory-First results[J]. Computers and Mathematics with Applications, 1999, 37: 19-31.

[4] Molodtsov D. The theory of soft set[M]. Moscow: URSS Publishers, 2004.

[5] Maji P K, Biswas R, Roy A R. Fuzzy soft sets[J]. Journal of Fuzzy Mathematics, 2001, 9(3): 589-602

[6] Maji P K, Biswas R, Roy A R. On intuitionistic fuzzy soft sets[J]. Journal of Fuzzy Mathematics, 2004, 12(3): 669-684.

[7] Yang X B, Lin T Y, Yang J Y, et al. Combination of interval-valued fuzzy set and soft set[J]. Computers & Mathematics with Applications, 2009, 58(3): 521-527.

[8] Jiang Y C, Tang Y, Chen Q M, et al. Interval-valued intuitionistic fuzzy soft sets and their properties[J]. Computers and Mathematics with Applications, 2010, 60: 906-918.

[9] Zhang W R. Bipolar fuzzy sets and relation: A computational framework for cognitive modeling and mulit-agent decision analysis[C]. Proceedings of the First Fuzzy International Joint Conference of the North American Society Binannual Conference, 1994: 305-309.

[10] Lee K M. Bipolar-valued fuzzy sets and their basic operations[J]. Proceedings of the International Conference, Bangkok, Thailand, 2000: 307-317.

[11] Lee K M. Comparison of interval-valued fuzzy sets, intuitionistic fuzzy sets, and bipolar-valued fuzzy sets[J]. Journal of fuzzy Logic Intelligent Systems, 2004, 14: 125-129.

[12] Abdullah S, Aslam M, Ullah K. Bipolar fuzzy soft sets and its applications in decision making problem[J]. Journal of Intelligent & Fuzzy Systems, 2014, 27(2): 729-742.

[13] 杨文华, 李生刚. 双极值模糊软集[J].计算机工程与应用, 2012, 48(35): 15-18.

[14] Maji P K, Biswas R, Roy A R. Soft set theory[J]. Computers and Mathematics with Applications, 2003, 45: 555-562.

[15] Shabir, Muhammad, Munazza. On bipolar soft sets[J]. arXiv Preprint arXiv: 2013, 1(1):1303-1344.

责任编校：孙 林

Research on Operation of Bipolar Fuzzy Soft Set and Its Application

HUA Feng-Bin, WANG Yan-ping

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

From the view of parameter set information, this paper introduces the concept of bipolar fuzzy soft set by integrating the bipolar soft set and fuzzy set firstly. Then the union intersection complement ‘and’ ‘or’ operations are defined, and its operation properties are proved. Finally, based on the bipolar fuzzy soft set, a decision algorithm is proposed to solve the problem of fund selection in the process of investment.

soft sets; bipolar soft sets; bipolar fuzzy sets; bipolar fuzzy soft sets

10.15916/j.issn1674-3261.2017.04.002

TP301；O236

A

1674-3261(2017)04-0215-06

2016-12-08

华逢彬(1990-)，男，山东临沂，硕士生。王艳平(1966-)，女，辽宁锦州人，教授，硕士。