多种垂向轮轨关系的对比及改进的车−线−桥系统迭代模型的建立
2017-10-14朱志辉王力东龚威余志武蔡成标
朱志辉,王力东,龚威,余志武,蔡成标
多种垂向轮轨关系的对比及改进的车−线−桥系统迭代模型的建立
朱志辉1, 2,王力东1,龚威1,余志武1, 2,蔡成标3
(1. 中南大学土木工程学院,湖南长沙,410075;2. 中南大学高速铁路建造技术国家工程实验室,湖南长沙,410075;3. 西南交通大学牵引动力国家重点实验室,四川成都,610031)
对比分析非线性赫兹接触、线性赫兹接触、刚性接触这3种轮轨接触模型对车−线−桥垂向耦合系统动力分析结果的影响,并建立改进的车−线−桥耦合系统迭代计算模型。车辆模型采用多体系统动力学建立,轨道−桥梁模型采用有限元方法建立,根据不同的轮轨接触模型,建立相应的轮轨力计算公式,并采用分离迭代法计算耦合系统振动响应。在数值算例中,以高速列车通过5跨简支梁桥为计算背景,对不同轮轨接触模型的仿真计算结果进行对比分析。针对传统车−线−桥耦合系统迭代计算模型计算效率低的问题,建立改进的迭代计算模型。研究结果表明:线性赫兹接触模型与非线性赫兹接触模型得到的车体加速度、轮轨力、钢轨和桥梁的位移和加速度均较吻合,但前者的计算效率较低;忽略轮对惯性力的刚性接触模型无法得到准确的钢轨和桥梁加速度;改进模型通过建立包含轮轨接触弹簧的车辆模型来提高车辆子系统的迭代稳定性,其计算效率比传统模型提高近7倍;为保证计算结果的准确性,车−线−桥耦合振动计算中应考虑时间步内的迭代计算。
车−线−桥耦合振动;轮轨接触模型;赫兹接触;刚性接触;迭代模型
列车通过桥梁时将引起桥梁结构振动,而桥梁振动又反过来影响车辆振动,这种相互作用、相互影响的问题就是车辆与桥梁之间的耦合振动问题[1]。根据所建立的不同车辆模型,通常可将车桥耦合振动模型分为垂向模型和空间模型。垂向模型通常只考虑车体和转向架的沉浮和点头运动,空间模型则可以考虑车辆横向及纵向运动[2]。当研究目标主要关注车桥系统垂向方向的相互作用时,可建立垂向车桥耦合计算模型,以简化分析难度,提高计算效率。垂向车桥耦合计算模型目前仍然是车桥耦合振动研究的重要模 型[3−5]。针对车桥垂向耦合振动仿真分析,建立合理的轮轨关系是关键。基于轮对和钢轨都是弹性体,采用非线性赫兹接触理论模拟轮轨关系成为主流[3]。然而,当考虑轮轨接触非线性时,会不可避免地带来如下问题[4, 6]:增加车桥耦合振动计算的复杂性,降低计算效率;无法进行频域车桥耦合振动分析;难以在有限元分析软件中建立轮轨非线性接触关系。为了简化计算或为了建立车桥线性时变系统,人们采用2 种方法建立考虑轮轨线性接触的轮轨关系:第1种是将非线性赫兹接触弹簧线性化,即线性赫兹接触[6];第2种是忽略轮轨之间的压缩变形,视轮轨接触为刚性接触[5]。不同轮轨接触模型的选择对车桥耦合振动仿真结果有重要影响。WANG等[7−9]通过建立考虑轮轨弹性接触和刚性接触的车桥耦合振动计算模型,对不同轮轨接触模型对车桥耦合系统的影响及其适用性进行了讨论。然而,以上研究主要侧重于轮轨非线性赫兹接触和刚性接触之间的对比,对轮轨线性赫兹接触的研究较少,而且计算所采用的桥梁模型通常不考虑轨道结构的参振作用。近年来,随着基于频域求解的随机振动理论的发展,更多学者采用此类随机振动理论研究车桥耦合振动问题[10−11],如何正确考虑轮轨线性接触关系成为关键。随着有限元建模技术的日趋成熟和计算机计算能力的不断提升,建立考虑轨道结构的精细化桥梁模型已成为车桥耦合振动领域发展的必然趋势。基于上述原因,本文作者以8车编组高速列车通过5跨简支箱梁桥为计算背景,通过建立考虑轮轨非线性赫兹接触、线性赫兹接触和刚性接触的车−线−桥耦合系统垂向振动模型,对多种轮轨接触模型的仿真计算结果进行对比分析。最后,针对传统车−线−桥耦合系统迭代计算模型计算效率低的问题,建立改进的迭代模型,并通过理论分析和数值算例对改进模型的计算结果和计算效率进行验证,讨论迭代计算对计算精度的影响。
1 车−线−桥垂向耦合振动计算模型
1.1 车辆模型
车辆模型如图1所示,采用多体系统动力学理论建立。其中车辆自由度包括车体的沉浮量(Z)和点头角度(c)、转向架1的沉浮量(t1)和点头角度(t1)、转向架2的沉浮量(t2)和点头角度(t2)以及4个轮对的沉浮量(w,=1~4)共10个自由度。图1中:c,t和w分别为车体、转向架和轮对的质量;pz和sz分别为车辆一系和二系悬挂系统的刚度;pz和sz分别为车辆一系和二系悬挂系统的阻尼系数;cy和ty分别为车体和转向架点头转动惯量;c为车辆定距的一半;t为车辆轴距的一半;为车速。表1所示为数值算例中使用的高速列车动车和拖车主要参数。当列车匀速运行时,不考虑车辆之间的纵向相互作用,则车辆子系统动力平衡方程为

式中:V,V和V分别为车辆子系统的质量矩阵、阻尼矩阵、刚度矩阵;V和V分别为车辆子系统的位移向量和力向量。
图1 车辆模型
Fig. 1 Vehicle model

表1 车辆参数
1.2 轨道−桥梁模型
轨道结构在列车、轨道和桥梁所组成的耦合振动大系统中起着非常重要的作用。详细考虑桥上轨道结构参振的影响,对于准确地模拟车−线−桥系统的动态相互作用关系具有非常重要的意义[12]。
本文采用有限元方法建立轨道−桥梁整体有限元模型。基于直接刚度法的轨道−桥梁子系统动力平衡方程可表示为

式中:B,B和B分别为轨道−桥梁子系统的总体质量矩阵、总体阻尼矩阵和总体刚度矩阵;B和B分别为轨道−桥梁子系统的位移和力向量。总体阻尼矩阵B包括桥梁本身的材料阻尼和轨下弹簧−阻尼器单元阻尼:
(3)
式中:和为Rayleigh阻尼系数,桥梁阻尼比取2%;e为具有单元阻尼的单元类型数;为第个弹簧−阻尼器单元的阻尼矩阵。
1.3 车−线−桥耦合系统动力方程及求解
联立式(1)和式(2)可建立车−线−桥耦合系统动力方程:
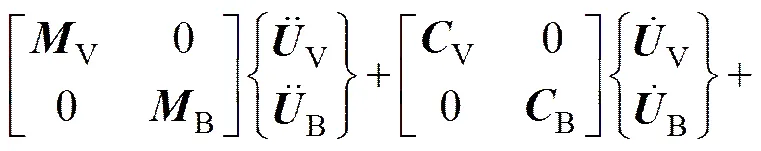
(4)
式中:2个子系统的力向量V和B体现轮轨相互作用关系。由于式(1)和式(2)右端互为相关,若在分析中将两者合并组成1个方程组同步求解,则不仅会使计算量大大增加,而且具有一定的近似性[9]。目前,大多将车辆子系统和轨道−桥梁子系统分开迭代求解,并通过轮轨接触处力的平衡条件和位移协调条件来控制迭代是否满足收敛要求。本文同样采用迭代法计算车−线−桥耦合系统动力响应,具体迭代流程图见文献[9]。
2 轮轨接触模型
2.1 非线性赫兹接触模型
根据非线性赫兹接触理论,轮轨垂向相互作用力()与轮轨弹性压缩量δ()之间有如下关系:
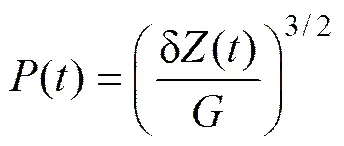
式中:为轮轨接触常数(m/N2/3),对于锥形踏面车轮,=4.57−0.149×10−8,对于磨耗型踏面车轮,=3.86−0.115×10−8;为车轮滚动圆半径(m)。根据式(5)得到的轮轨压缩量和轮轨垂向力之间的关系是1条下凹的曲线,见图2中曲线1。当轮轨界面存在轨道不平顺附加位移()输入时,轮轨力的表达式为
(6)
其中:w()为轮对垂向位移;r()为轮轨接触处的钢轨垂向位移。
2.2 线性赫兹接触模型
线性赫兹接触模型假设轮轨之间通过线性化的弹簧联结,此时,轮轨相互作用力()可表示为
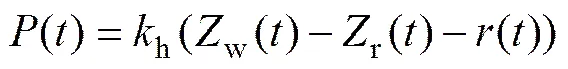
针对线性赫兹接触弹簧刚度系数h,目前主要有2种取值方法,分别是切线斜率法[6]和割线斜率法[4]。
2.2.1 切线斜率法
切线斜率法是指过非线性赫兹接触曲线中静态轮轨力0对应的0点作切线,切线的斜率即为h,如图2中曲线2。具体求解过程如下。

图2 非线性和线性赫兹接触曲线
将式(5)中()对δ()求导即可得非线性赫兹接触刚度的表达式:
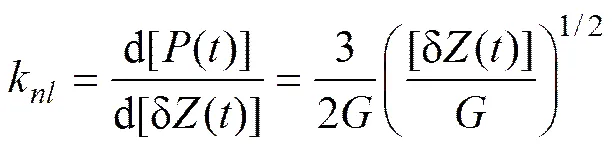
此时,将静态轮轨力0对应的轮轨静压缩量δ0()代入式(8),即可得0点切线的斜率:
(9)
2.2.2 割线斜率法
割线斜率法是指取非线性赫兹接触曲线中静态轮轨力0对应的0点和轮轨力变化范围中最大值1对应的1点的连线斜率作为h,如图2点中曲线3,具体求解过程如下。
将式(5)中轮轨压缩量表示为轮轨垂向力的函数:

此时,0点的坐标可以表示为(,0),1点的坐标可以表示为(,1),因此,0点和1点连线的斜率为
(11)
2.3 刚性接触模型
当假设轮轨刚性接触时,车轮和钢轨之间始终密贴,且具有相同自由度[5],此时,轮轨之间的相互作用力包括车辆一系悬挂系统中的弹簧力和阻尼力、轮对惯性力以及车辆轴重力3部分。车辆不同轮对的轮轨力为:

(12)

(14)
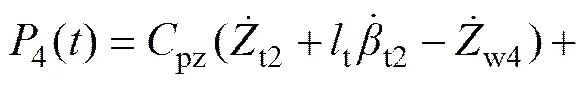
(15)
式中:第(=1~4)轮对的垂向位移wi可由轮轨接触处的钢轨垂向位移ri()和轨道高低不平顺附加位移r()相加得到,即

当假设轮轨刚性接触时,若轮对质量大于轮下节点集中质量,则将导致迭代发散[1, 13]。为提高系统迭代计算的稳定性,文献[1]提出忽略轮对惯性力对钢轨的作用,文献[13]提出了虚拟质量法。
3 数值算例
以我国高速铁路总里程中比例最大的32 m预应力混凝土简支箱梁桥为研究对象,建立如图3所示的轨道−桥梁子系统有限元模型。桥梁模型按5跨简支梁建立,墩高为18 m,主梁和桥墩截面如图4所示。在有限元模型中,主梁和桥墩均采用空间梁单元离散。轨道结构选用高速铁路双块式无砟轨道,轨道的弹性主要靠轨下胶垫提供,轨枕和道床板的作用通过参振质量的形式在桥梁动力学模型中加以考虑[14]。在有限元模型中,钢轨参数选用我国60 kg/m钢轨,采用空间梁单元离散,并通过刚臂考虑线路偏心。钢轨节点和刚臂节点之间通过弹簧−阻尼器联结,考虑轨下扣件和垫板的弹性支撑作用,垂向刚度和阻尼分别为4.76×107N/m和7.5×104N·s/m,横向刚度和阻尼分别为2.5×107N/m和6×104N·s/m。据文献[14],桥面二期恒载取160 kN/m。
根据表1给出的车辆参数按8车编组(1M+6T+1M)形成车辆系统,车速设为250 km/h,轮轨竖向激扰采用由德国低干扰轨道不平顺谱变换得到的轨道不平顺时域样本。为模拟列车进入桥梁之前的初始振动状态,计算时假定列车从距桥头30 m处开始作匀速运动。
本文选用5种不同的轮轨接触模型进行车−线−桥耦合振动分析,分别为:非线性赫兹接触(NH)、基于切线斜率法的线性赫兹接触(TLH)、基于割线斜率法的线性赫兹接触(SLH)、忽略轮对惯性力的刚性接触(NMC)和采用虚拟质量法的刚性接触(VMC)。其中,基于切线斜率法的动车和拖车的轮轨接触刚度分别为1.52 GN/m和1.47 GN/m,基于割线斜率法的动车和拖车的轮轨接触刚度分别为1.62 GN/m和1.57 GN/m,即取1=1.450[15];采用虚拟质量法计算时,虚拟质量等于轮对质量。

图3 轨道−桥梁模型
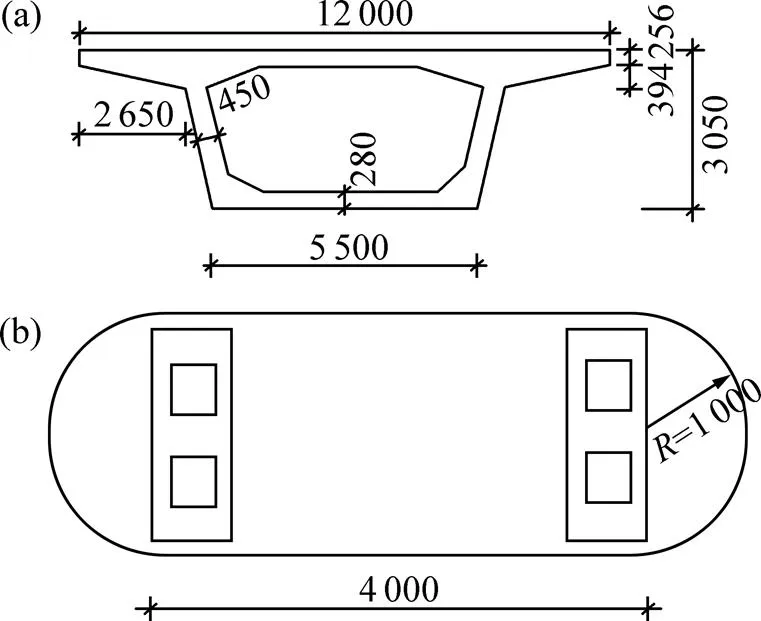
(a) 主梁截面;(b) 桥墩截面
不同轮轨力计算模型得到收敛结果的最大积分步长并不相同,一般需满足各子系统的最高频率、作用荷载频率的限制[13]。结合计算条件,将不同轮轨接触模型对应的时间积分步长设定如下:非线性赫兹接触取1×10−4s,线性赫兹接触取2×10−5s,密贴接触取1×10−3s。其中,2×10−5s为本文计算条件下线性赫兹接触模型的最大收敛时间积分步长。
不同轮轨接触模型下中跨跨中桥梁垂向加速度见图5,不同轮轨接触模型下车−线−桥系统垂向响应最大值及计算效率对比见表2。从图5和表2可见:
1) 线性赫兹接触模型与非线性赫兹接触模型计算得到的车体加速度、轮轨力、钢轨和桥梁的位移和加速度均较吻合。除SLH计算得到的钢轨加速度与NH计算的钢轨加速度相对误差为5.5%以外,其他计算结果相对误差均在1.5%以内,满足数值模拟对计算精度的要求。另一方面,由于采用切线斜率法得到的轮轨接触刚度比割线斜率法的小,因此,TLH计算的钢轨振动加速度比SLH的小,且与NH所得结果更接近。
2) 由于线性赫兹接触刚度大,通常为1 GN/m,因而,任意2个荷载步之间的轮轨压缩量变化不能过大,否则容易导致迭代发散。因此,线性赫兹接触通常需要比非线性赫兹接触更小的积分步长。在本文计算中,线性赫兹接触的计算效率为非线性赫兹接触计算效率1/7左右。
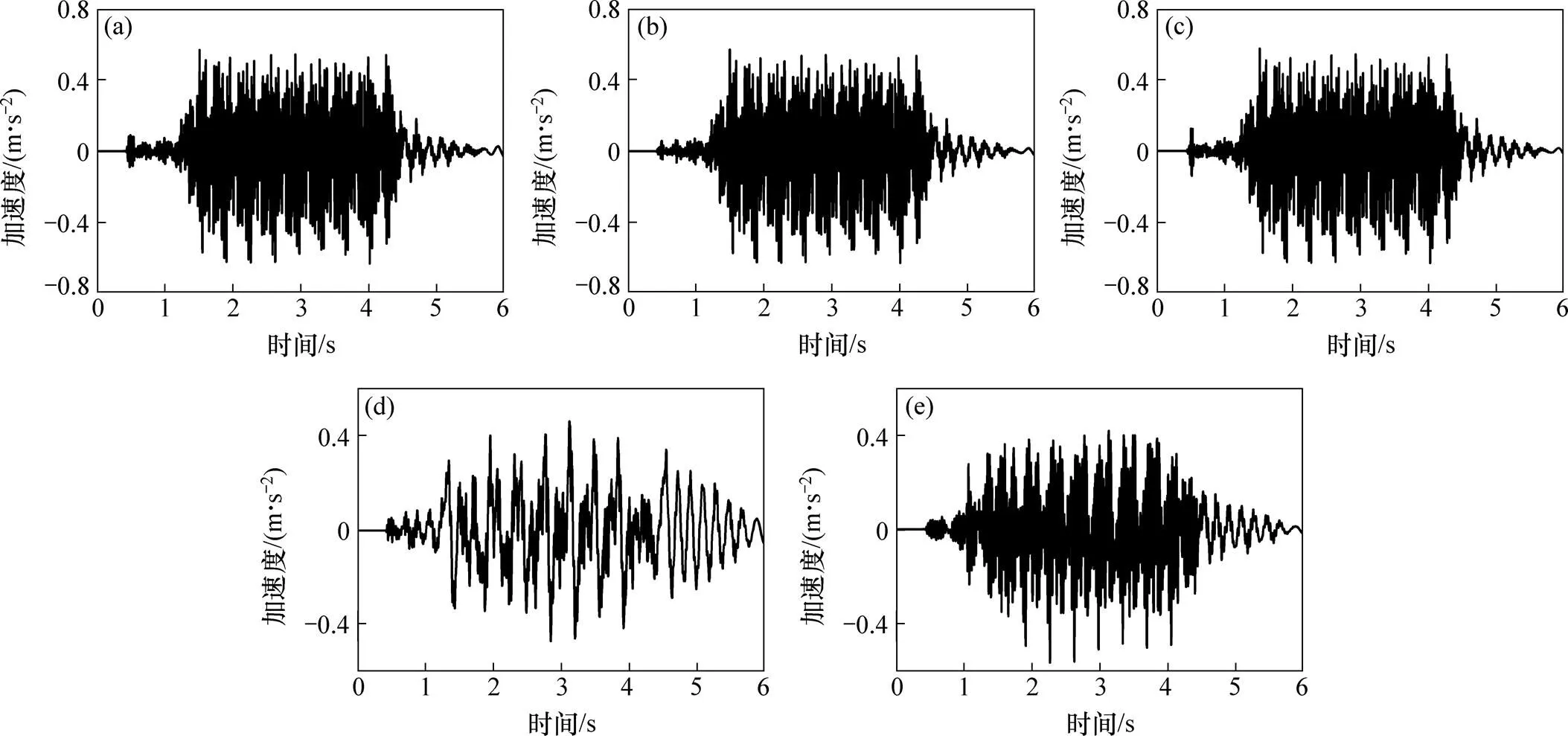
模型:(a) NH;(b) TLH;(c) SLH;(d) NMC;(e) VMC

表2 不同轮轨接触模型下车−线−桥系统垂向响应最大值及计算效率对比
3) 忽略轮对惯性力对钢轨的作用无法得到准确的钢轨和桥梁加速度、轮轨力。忽略轮对惯性力使得钢轨加速度、桥梁加速度、轮轨力等评价桥梁动力特性和车辆走行性的关键指标远远比赫兹接触模型的小。其原因在于当车桥耦合振动分析中考虑轨道结构时,轮轨力作用下的钢轨的加速度远大于梁体的加速度,使得轮对惯性力占轮轨力的比例大大增加,此时忽略轮对惯性力将严重削弱轮轨动态相互作用,从而无法得到正确的计算结果。
4) VMC方法虽然可以提高轮轨刚性接触下车−线−桥系统的迭代稳定性,但计算误差偏大。由于轮轨刚性接触忽略轮轨之间的相对运动削弱了车轮对钢轨的冲击作用,使得钢轨和桥梁加速度计算结果偏小。同时,在本文计算条件下,VMC方法所需计算时间为835 min,大大降低了计算效率。这是因为增加虚拟质量后,与轮对无耦合作用的钢轨节点的迭代谱半径随积分步长的减小而增大。
综上可知,当采用迭代法计算车−线−桥耦合振动时,为得到满足精度的计算结果,建议采用赫兹接触模型。
4 改进的车−线−桥系统迭代计算 模型
由前面分析结果可知,虽然线性赫兹接触模型与非线性赫兹接触模型计算结果十分接近,但线性赫兹接触模型存在积分步长小、计算效率低等问题。为提高基于轮轨线性赫兹接触的车−线−桥耦合系统传统迭代模型的计算效率,建立改进的迭代模型。改进模型是通过建立包含轮轨接触弹簧h的车辆模型来提高车辆系统的迭代稳定性。轮轨线性赫兹接触下简化的车−线−桥系统传统迭代模型和改进迭代模型见图6。
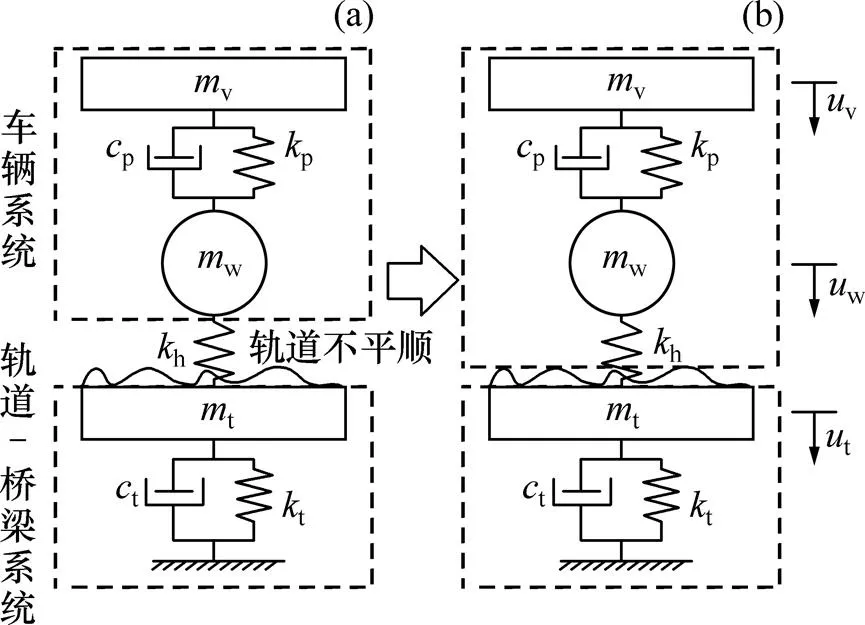
(a) 传统模型;(b) 改进模型
4.1 谱半径分析
对于车−线−桥耦合迭代计算模型,可以通过建立耦合系统动力方程前后迭代步之间的递推关系,并根据迭代矩阵的谱半径来判断迭代稳定性[1]。因此,本文采用图6所示简化的车−线−桥系统来对比改进前、后2种模型的迭代稳定性。
依据D’Alembert原理,图6(a)所示传统模型基于平衡位置的车体−轮对质量块的动力平衡方程可以表示为:
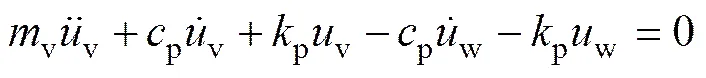
(18)
轮下质量块的动力平衡方程可以表示为

其中:,和分别为质量、阻尼和刚度;为位移;下标v,w和t分别表示车体质量块、轮对质量块和轮下质量块;下标p表示车辆悬挂系统,ir表示轨道不平顺;h为轮轨接触刚度系数;为重力加速度。
相对于传统迭代模型,图6(b)所示改进模型的轮对质量块动力平衡方程为

因此,改进模型在时间步上第次和第+1次迭代之间的直接迭代格式为
(21)
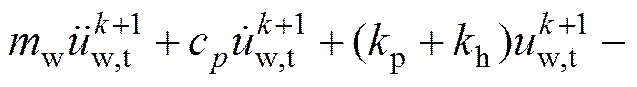
(23)
以Newmark−法数值积分格式为例,根据式(21)~(23)可建立改进模型在时刻上的迭代计算格式:

其中:
(25)
上标T表示转置;为迭代矩阵。的其非零元素为
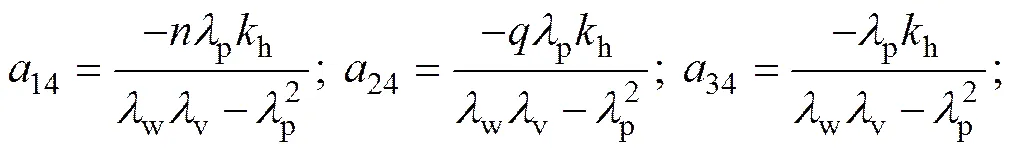
(26)
其中:
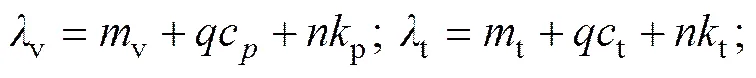
(27)
常数项()为上一时间步系统运动状态、轨道不平顺以及车辆重力的函数,因与收敛性无关,无需给出具体形式。通过求解迭代矩阵的特征值多项式,得相应的谱半径为

其中:
(29)
通过与上述类似的分析过程,可得传统模型的迭代矩阵谱半径为
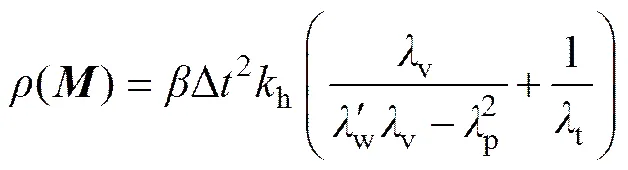
其中:
(31)
根据一般高速列车的车辆参数,可以近似假定图6所示的简化模型系统参数为:v=6.8 t,w=1.2 t,t=36 kg,p=1.04 MN/m,p=4.0×104N·s/m,t=1.6×108N/m,t=5.2×106N·s/m,h=1.35 GN/m。根据式(28)和式(30)可得出改进模型和传统模型的迭代矩阵谱半径随积分步长的变化规律,见图7。
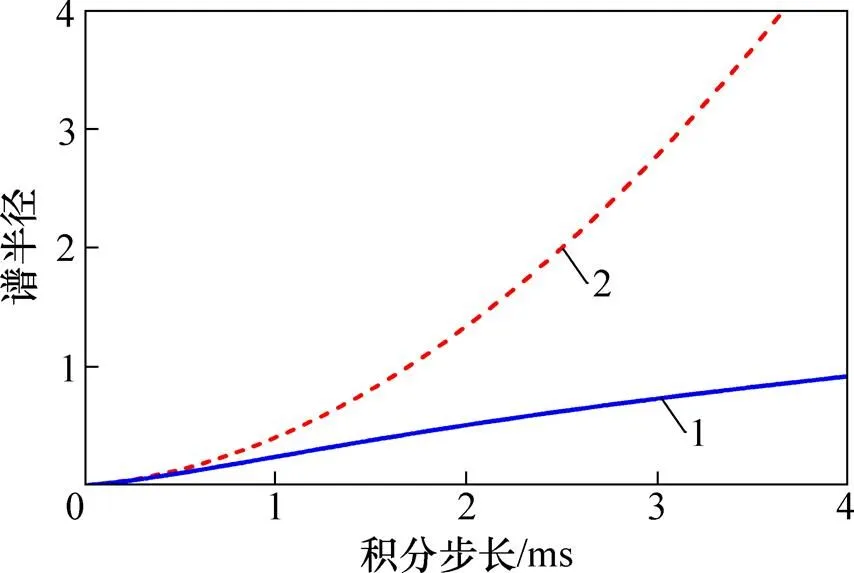
1—改进模型;2—传统模型。
从图7可以看出:改进模型和传统模型的迭代矩阵谱半径随积分步长的变化具有完全不同的变化趋势;传统模型的谱半径随着积分步长的增大呈开口向上的抛物线形状递增,而改进模型的谱半径随积分步长的增大以较缓慢的趋势递增,且在相同积分步长下改进模型的谱半径均比传统模型的小。出现上述差异的原因是通过建立包含轮轨接触刚度的改进模型,降低了车辆子系统随积分步长的敏感程度,提高了车−线−桥耦合系统的迭代稳定性。
4.2 数值算例
采用与第3节相同的计算条件,对比传统模型和改进模型的计算精度和计算效率,其中轮轨接触刚度采用切线斜率法计算。当积分步长取1×10−4s时,本文提出的改进模型可得到收敛的计算结果。图8所示为传统模型和改进模型的车−线−桥耦合系统计算结果,表3所示为传统模型与改进模型的车−线−桥系统垂向响应最大值及计算效率对比。
从图8可以看出:改进前、后2种模型得到的桥梁及车辆动力时程曲线几乎完全一致。表3所示的响应最大值中,除钢轨加速度存在2.4%的相对偏差外,其他响应的最大值几乎完全相同。就计算时间而言,传统模型需677 min,而改进模型仅需103 min。与传统模型相比,改进模型的计算效率提高了近7倍。
为进一步考察迭代计算对计算精度的影响,基于改进的迭代计算模型,分别计算考虑迭代和不考虑迭代下车−线−桥耦合系统振动响应,积分步长均取1×10−4s。
2种情况下车−线−桥耦合系统垂向响应最大值见表4。从表4可以看出:不考虑迭代对钢轨和桥梁位移的影响很小,而对其他计算结果的影响偏大,其中钢轨加速度增大22%,车体加速度减小11%。因此,为保证计算结果的准确性,车−线−桥耦合振动计算中需考虑时间步内的迭代计算。
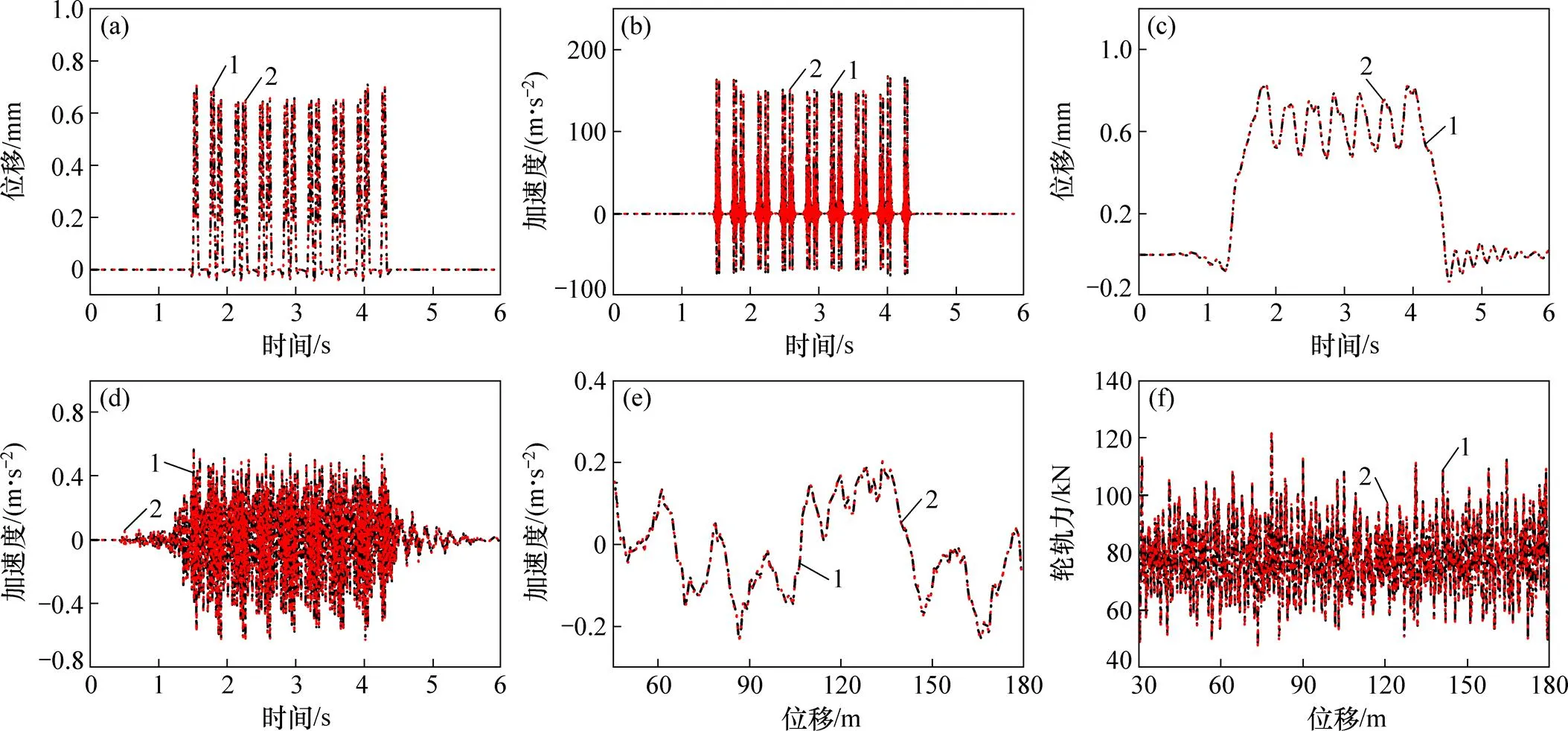
(a) 中跨跨中左轨垂向相对桥面位移;(b) 中跨跨中左轨垂向加速度;(c) 中跨跨中桥梁垂向位移;(d) 中跨跨中桥梁垂向加速度;(e) 首节车车体垂向加速度;(f) 首轮对轮轨垂向力之一半

表3 传统模型与改进模型的车−线−桥系统垂向响应最大值及计算效率对比

表4 考虑迭代和不考虑迭代下改进模型的车−线−桥系统垂向响应最大值
5 结论
1) 线性赫兹接触模型与非线性赫兹接触模型得到的车体加速度、轮轨力、钢轨和桥梁的位移和加速度均较吻合,但其计算效率为后者的1/7左右;基于切线斜率法的轮轨接触刚度模型计算轮轨力更准确。
2) 忽略轮对惯性力对钢轨的作用无法得到准确的钢轨和桥梁加速度。由于轮轨力作用下的钢轨加速度远比梁体的加速度大,使得相对于不考虑轨道结构时的轮对惯性力占轮轨力的比例大大增加,此时,忽略轮对惯性力将严重削弱轮轨动态相互作用,从而无法得到正确的计算结果。
3) 虚拟质量法会影响数值计算精度。增加虚拟质量降低了桥梁的自振频率,导致桥梁跨中位移偏大;同时,由于刚性接触无法考虑轮轨高频相互作用,使得钢轨和桥梁加速度、轮轨力等计算结果偏小。
4) 改进模型比传统模型的计算效率提高了近7倍。为保证计算结果的准确性,车−线−桥耦合振动计算中应考虑时间步内的迭代计算。
[1] 吴定俊, 李奇, 陈艾荣. 车桥耦合振动迭代求解数值稳定性问题[J]. 力学季刊, 2007, 28(3): 405−411. WU Dingjun, LI Qi, CHEN Airong. Numerical stability of iteration scheme for solution of vehicle−bridge coupling vibration[J]. Chinese Quarterly of Mechanics, 2007, 28(3): 405−411.
[2] 王宁波, 任伟新, 肖祥. 列车−桥梁耦合振动研究综述[J]. 力学进展, 2012, 42(5): 634−643. WANG Ningbo, REN Weixin, XIAO Xiang. The state of art of study on vehicle−bridge coupling vibration[J]. Advances in Mechanics, 2012, 42(5): 634−643.
[3] 郑国琛, 祁皑, 颜学渊. 考虑车轨垂向耦合福州地铁振源加速度研究[J]. 振动、测试与诊断, 2015, 35(2): 328−401. ZHENG Guochen, QI Ai, YAN Xueyuan. Research on acceleration of vibration source from Fuzhou metro considering vehicle−track vertical coupled model of vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(2): 328−401.
[4] 周毅. CRTSⅢ型板式轨道减振特性研究[D]. 成都: 西南交通大学土木工程学院, 2011: 14−16. ZHOU Yi. Research on vibration−reduction performance of CRTSⅢslab ballastless track[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2011: 14−16.
[5] LU Feng, LIN Jiahao, KENNEDY D, et al. An algorithm to study non-stationary random vibrations of vehicle–bridge systems[J]. Computers and Structures, 2009, 87(3): 177−185.
[6] 全顺喜. 高速道岔几何不平顺动力分析及其控制方法研究[D]. 成都: 西南交通大学土木工程学院, 2012: 49−50. quan shunxi. Study on dynamic analysis and coutrol methods of the geometric irregularity in high-speed turnout[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2012: 49−50.
[7] WANG Tonlo, CHU Kuanghan. Railway bridge/vehicle interaction studies with new vehicle model[J]. Journal of Structural Engineering, 1991, 117(7): 2099−2116.
[8] 葛玉梅, 袁向荣. 机车−桁架桥梁耦合振动研究[J]. 西南交通大学学报, 1998, 33(2): 138−142. GE Yumei, YUAN Xiangrong. Study on dynamic interacttion between a moving locomotive and a steel−truss bridge[J]. Journal of Southwest Jiaotong University, 1998, 33(2): 138−142.
[9] 林玉森, 李小珍, 强士中. 车桥耦合振动中2种轮轨接触模型的比较分析[J]. 中国铁道科学, 2007, 28(6): 70−74. LIN Yusen, LI Xiaozhen, QIANG Shizhong. Contrast analysis of two wheel−rail contact models in the coupling vibration of vehicle−bridge system[J]. China Railway Science, 2007, 28(6): 70−74.
[10] PABLO A, ZHANG Nan, GOICOLEA JOSE M, et al. Consideration of nonlinear wheel–rail contact forces for dynamic vehicle–bridge interaction in high-speed railways[J]. Journal of Sound and Vibration, 2013, 332(5): 1231−1251.
[11] 余志武, 毛建锋, 谈遂, 等. 车桥竖向随机振动的概率密度演化分析[J]. 中南大学学报(自然科学版), 2015, 46(4): 1420−1426. YU Zhiwu, MAO Jianfeng, TAN Sui, et al. Probability density evolution analysis of track−bridge vertical coupled vibration with irregularity random excitation[J]. Journal of Central South University (Science and Technology), 2015, 46(4): 1420−1426.
[12] 翟婉明, 夏禾. 列车−轨道−桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011: 212−213. ZHAI Wanming, XIA He. Train−track−bridge dynamic interaction: theory and engineering application[M]. Beijing: Science Press, 2011: 212−213.
[13] 夏禾, 张楠, 郭薇薇, 等. 车桥耦合振动工程[M]. 北京: 科学出版社, 2014: 120−126. XIA He, ZHANG Nan, GUO Weiwei, et al. Coupling vibration of train−bridge system[M]. Beijing: Science Press, 2014: 120−126.
[14] 朱志辉, 余志武, 朱玉龙, 等. 车−桥振动诱发周围环境及建筑物振动分析[J]. 铁道学报, 2013, 35(4): 102−109. ZHU Zhihui, YU Zhiwu, ZHU Yulong, et al. Analysis on environment and building vibration induced by passing trains on bridge structures[J]. Journal of the China Railway Society, 2013, 35(4): 102−109.
[15] 范俊杰. 现代铁路轨道[M]. 2版. 北京: 中国铁道出版社, 2004: 6−7. FAN Junjie. Modern railway track[M]. 2nd ed. Beijing: China Railway Publishing Press, 2004: 6−7.
(编辑 陈灿华)
Comparative analysis of several types of vertical wheel/rail relationship and construction of an improved iteration model for train−track−bridge system
ZHU Zhihui1, 2, WANG Lidong1, GONG Wei1, YU Zhiwu1, 2, CAI Chengbiao3
(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High Speed Railway Construction,Central South University, Changsha 410075, China;3. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)
The influence of three types of wheel, i.e. rail contact model−nonlinear Hertz contact, linear Hertz contact and rigid contact on the dynamical analysis result of train−track−bridge vertical coupled system were compared, and an improved iteration model for train−track−bridge coupled system was established. The vehicle model was established by multi−body system dynamics and the track−bridge model was established by finite element method. Depending on different wheel−rail contact models, the corresponding wheel−rail force calculation formulas were established, and the iterative method were used to calculate the coupled system vibration. In numerical case, taking a high-speed train traveling across a five-span simply supported beam bridge for case study, the calculation results of train−track−bridge coupled vibration withr different wheel−rail contact models were compared. Aiming at the problem of low efficiency of the iterative computation model for the traditional train−track−bridge coupled system, an improved iteration model was established. The results show that the vehicle body acceleration, wheel-rail force, displacement and acceleration of the rail and bridge of the linear Hertz contact model are in good agreement with those of the nonlinear Hertz contact model, but the computational efficiency is lower than that of the latter; rigid contact model which neglects the inertia force of the wheel is unable to obtain accurate rail and bridge acceleration. The improved model is to improve the iterative stability of the vehicle subsystem by establishing the vehicle model including the wheel−rail contact spring. The calculation efficiency of improved model is about 7 times greater than that of the conventional model. In order to ensure the accuracy of results, the iterative calculation in the time step should be taken into account in the calculation of train−track−bridge coupled vibration.
train−track−bridge coupled vibration; wheel−rail contact model; Hertz contact; rigid contact; iteration model
10.11817/j.issn.1672−7207.2017.06.023
U238;TU248
A
1672−7207(2017)06−1585−09
2016−07−15;
2016−09−22
国家自然科学基金资助项目(51378511,51678576);湖南省自然科学基金资助项目(13JJ5007);牵引动力国家重点实验室开放基金资助项目(TPL1601);中南大学中央高校基本科研业务专项资金资助项目(2016zzts070)(Projects(51378511, 51678576) supported by the National Natural Science Foundation of China; Project(13JJ5007) supported by the Natural Science Foundation of Hunan Province; Project(TPL1601) supported by the Open Project Foundation of State Key Laboratory of Traction Power; Project(2016zzts070) supported by the Fundamental Research Funds for the Central Universities of Central South University)
朱志辉,博士,副教授,从事车桥耦合振动研究;E-mail:zzhh0703@163.com
