饱和砂土场地微差爆炸液化的试验与数值分析
2017-10-14姚颖康王维国贾永胜陈育民
姚颖康,王维国,贾永胜,陈育民
饱和砂土场地微差爆炸液化的试验与数值分析
姚颖康1, 2,王维国2,贾永胜1,陈育民2
(1. 武汉市市政建设集团有限公司,湖北武汉,430023;2. 河海大学土木与交通学院,江苏南京,210098)
基于大型饱和砂土场地的多点微差爆炸液化试验,建立全耦合数值计算方法对试验过程进行模拟和验证,并分析爆炸延时、药包总质量等对土中超孔隙水压力上升的影响。研究结果表明:基于数值计算结果建立的多点爆炸液化经验公式能较好地反映超孔隙水压力比随比例距离的关系。场地中心区域更易受到爆炸波叠加作用的影响,当爆炸延时从110 ms增至330 ms时,超孔隙水压力可以提高18%以上;超孔隙水压力随着总药量的增加明显增大,增长趋势却逐渐减小。
饱和砂土;微差爆炸;爆炸液化;超孔隙水压力;数值模拟
地震、冲击和爆炸等荷载作用下饱和砂土的液化问题是防灾减灾领域重要的研究课题[1]。随着城市地下爆破工程实施数量增多以及偶然爆炸事故和恐怖袭击的潜在威胁,由爆炸振动引起的饱和土体液化问题逐渐成为新的研究热点[2−3]。我国沿海局部地区广泛分布着高水位的砂土层,地下爆破或爆破拆除作业均是引起地基液化的潜在危险源,同时沿海经济发达区域仍是战时军事打击的主要目标,因此,开展爆炸荷载作用下饱和土体的液化特性研究具有重要的意义。爆炸荷载引起的土中超孔隙水压力上升、地表质点振动、土体应变等参量常作为评价饱和土爆炸液化的标 准[4]。STUDER等[5]基于饱和砂土中的单药包爆炸试验,提出了基于药量和爆距的爆炸液化经验公式。ASHFORD等[6]开展了原位场地的多药包爆炸液化试验研究,分析了药量、药包布置等爆炸参数,并制造了大面积振动液化环境。王兰民等[7]利用人工微差爆破地震动模拟天然地震动强度与振次,证实了黄土液化的客观存在性。现有研究结果表明,利用微差爆炸模拟地震液化环境的手段可以作为振动模拟环境的补充方法。然而,目前对于多点微差爆炸液化试验的参数设计和优化仍依赖经验和试点试验。为开展大型振动液化场地RC结构和土质堤坝的灾变试验,需要对爆炸参数进行优化。由于土中爆炸问题的复杂性,试验是进行爆炸参数优化的首要方法。开展爆炸试验往往受限于技术难度、风险、可重复性以及成本等因素,而经过试验验证的数值方法可以作为爆炸试验的验证及补充。张智超等[8−9]利用LS-DYNA有限元软件对饱和土中爆炸引起的超孔隙水压力进行了数值模拟,验证了LS-DYNA在分析爆炸液化问题中的可行性和有效性。因此,本文作者基于室外大型饱和砂土场地开展的多点微差爆炸液化的试验,建立全耦合数值计算方法,以验证数值手段的有效性和可行性,并在此基础上对药量、延时等参数进行优化分析。研究结果可以为全尺寸爆炸液化试验的设计参数提供切实有效的依据和参考。
1 爆炸液化效应
饱和的砂土或粉土受到动荷载作用,在当排水不良时,土中孔隙水压力上升从而导致土体有效应力减小,并最终使得固体介质逐渐转变为一种黏性流体的变化或行为定义为土体液化[10]。爆炸荷载具有瞬时高冲击的特性。爆炸产生的高温高压爆轰气体使药包周围局部土体发生严重塑性变形呈流态,甚至气化而形成不稳定的空穴。由于饱和土体中空隙含量微乎其微,无法对爆炸冲击形成吸收削弱作用,不可压缩的孔隙水直接承受爆炸冲击作用,最终导致土中孔隙水压力的急剧上升。炸药在饱和土中爆炸后土中孔隙水压力的响应一般经历3个阶段,即爆后瞬时由爆炸直接冲击引起的峰值孔隙水压力上升、爆炸波传播后的短时超孔隙水压力的累积以及爆后相对较长时间的消散过程[4]。超孔隙水压力比(u)是最常用的饱和土液化发生的评价标准之一,为土中超孔隙水压力非峰值增量(Δ)与土体的初始竖向有效应力()之比,用于描述饱和土中液化发生的程度:
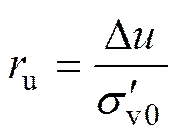
当u达到1.0时,饱和土体处于完全液化状态,而当u<0.1时可以忽略超孔隙水压力上升的影响。对于指定场地,药量和爆距是决定饱和土中超孔隙水压力响应的最主要因素。比例距离()综合考虑了药量和径向爆距的因素,便于对不同形式炸药与爆距条件下的测点进行对比。通过量纲分析,适用于单孔集中药包的立方根比例距离的量纲一形式可以表示为(其中:为爆炸能量,e为炸药密度,s为土中地震波速度,为离开爆源的距离)。当炸药以TNT当量衡量时,可以用炸药当量TNT代替爆炸能量,对于多点集中炸药爆炸,采用总质量及平均爆距(),最终可以将比例距离的量纲一的形式转变成更方便的形式[11]:
(2)
现阶段爆炸液化的判别主要通过系统地对试验数据进行数学统计分析,得到简化后的孔隙水压力与比例距离、初始竖向有效应力和相对密实度等因素的经验关系,以此来预测特定条件下爆炸液化的可能范围及液化程度。然而,现有的经验判别模型往往局限于特定的场地条件和特定的爆炸参数,不一定适用于某一特定爆炸液化试验的预测。
2 问题描述
大型爆炸试验坑的上、下截面均为规则的圆形,深度为3 m,直径分别为19和16 m,如图1 所示。坑内回填砂土为长江灰细砂,饱和密度为1 835 kg/m3,黏粒质量分数为1%~1.5%,土粒相对密度为2.633,平均粒径为0.18 mm,不均匀系数为2.11,其级配曲线如图2所示。现场CPT试验结果表明:沿深度方向饱和砂土层的初始相对密实度为30%~35%。
爆炸液化试验选用的2号岩石乳化炸药密度为0.95~1.10 g/cm3,爆速为3 600 m/s。该炸药在饱和土中的爆燃性能可以近似以水下爆轰性能衡量,根据水下爆轰试验结果,该炸药的等效TNT当量系数为0.8[12]。饱和土中发生封闭爆炸的临界埋深通常需达到2.5 m/kg1/3以上[13−14],因此,试验中设计3个质量均为0.6 kg的乳化炸药,埋置半径和深度分别为6 m和2 m(图1),尽量使爆炸能量作用于土中孔隙水压力的上升。药包E5-E6-E7依次起爆,相邻药包起爆间隔为110 ms。
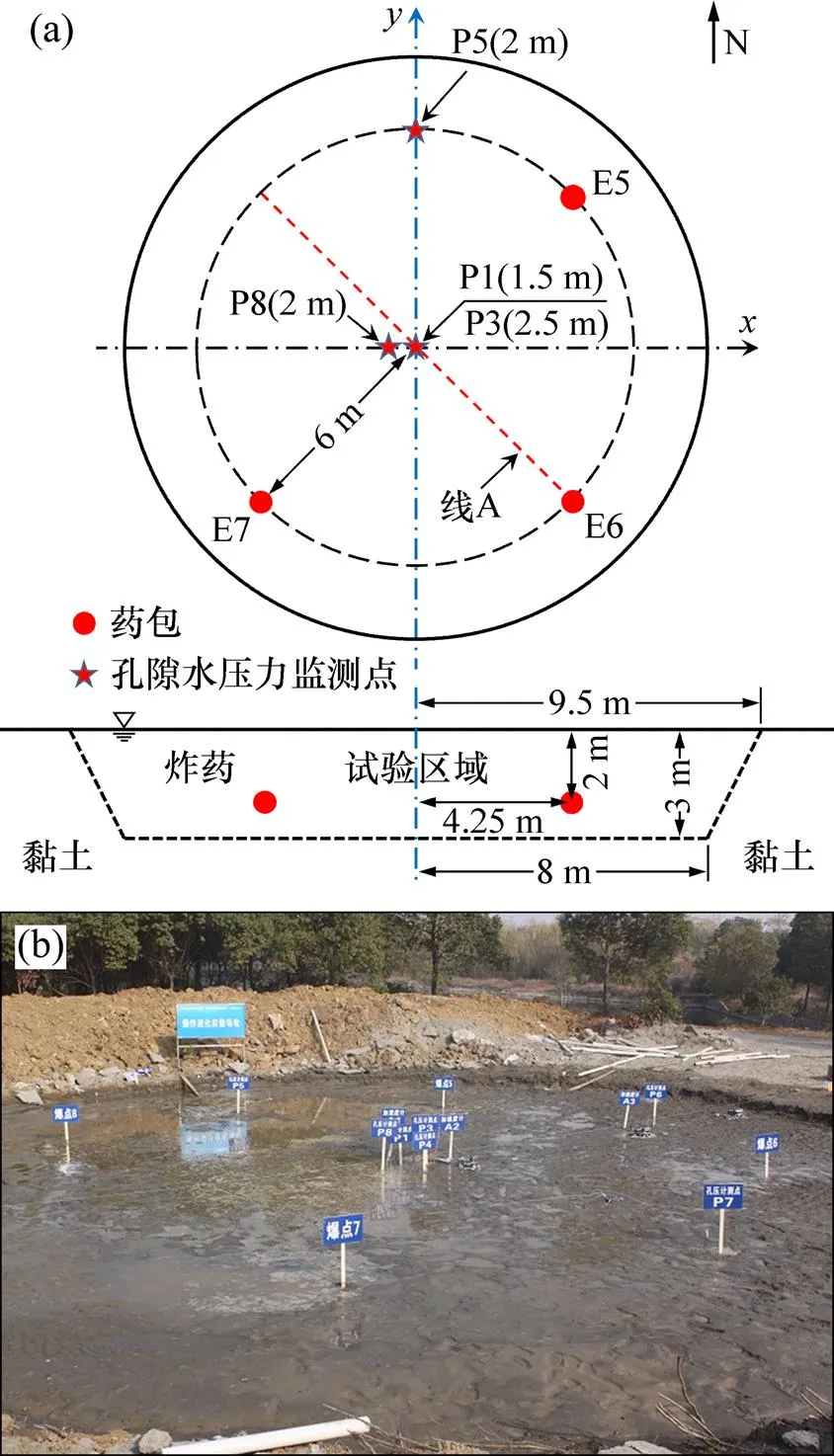
(a) 药包和传感器布置;(b) 饱和后试验场地实景
孔隙水压力的监测和采集设备包括:1) 岩土爆破专用CYY2型孔隙水压力传感器,量程为1.0 MPa,埋设位置及埋设深度处的初始竖向有效应力如图1和表1所示;2) XH5861型高速动态应变采集系统,试验中每通道数据采集频率为11 kHz,以最大可能地获得爆炸瞬间由冲击压缩效应造成的峰值孔隙水压力。
药包起爆后约2 min,试验坑内靠近药包E7附近区域出现冒水喷砂现象,表明该区域已经发生了液化,如图2所示。其他爆点附近也能观测到同样的现象,但场地中心附近并不可以观测到直接的液化现象,液化发生是个随机过程,与场地内土体松软差异、排水通道等因素有关,液化现象和孔隙水压力并不一定完全对应。经分析场地中心区域超孔隙水压力比的时程曲线(图3)并结合表1结果,在场地中心的药包布置平面及以下区域并未达到完全液化状态。
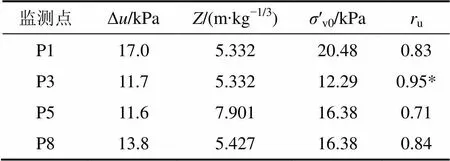
表1 监测点实测超孔隙水压力
* 竖向有效应力按实际测点深度计算。
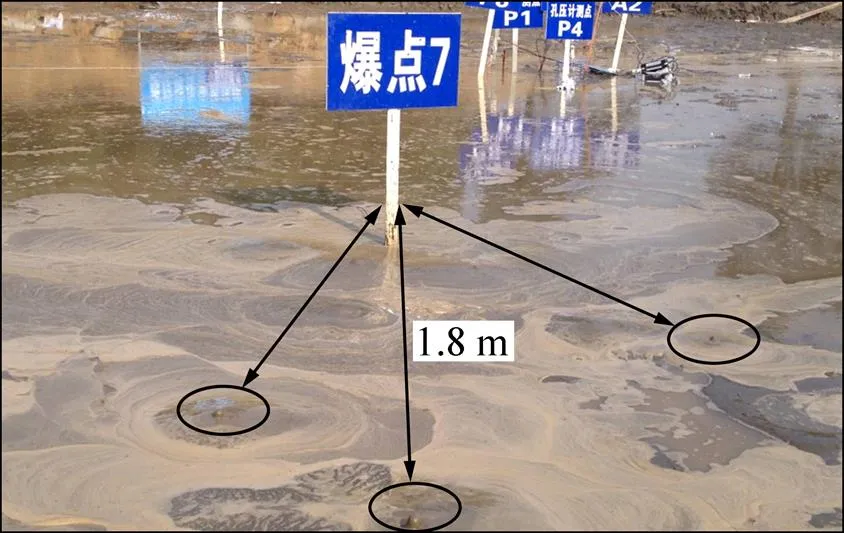
图2 试验场地爆后的砂沸现象
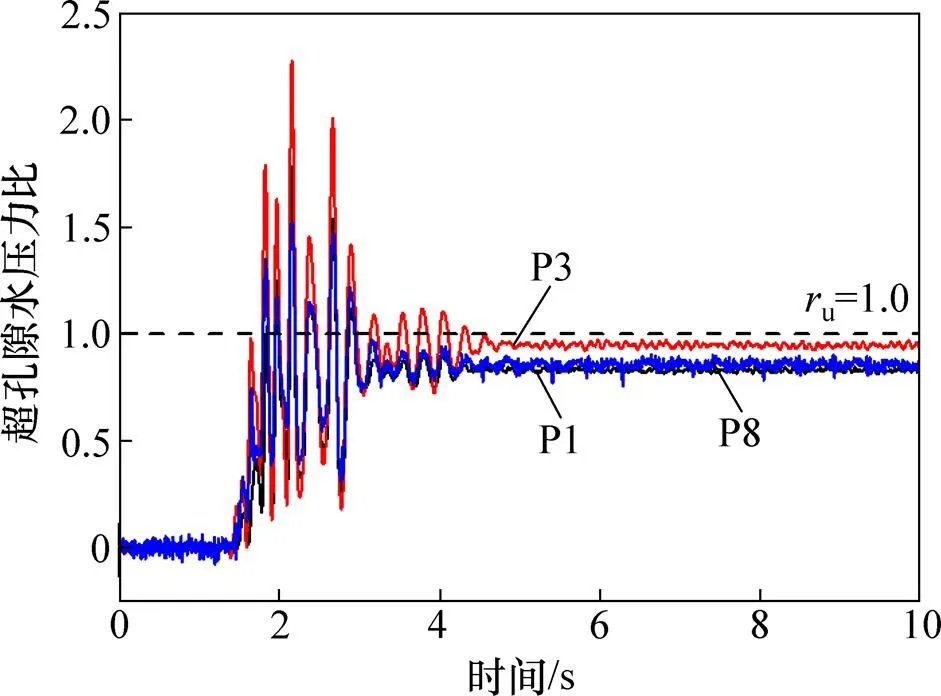
图3 场地中心区域超孔隙水压力比时程曲线
3 数值验证
3.1 数值计算参数及模型
显式拉格朗日算法以物质坐标为基础,将所描述的单元网格固定于物质上,并且随着物质而运动或变形,其有限元节点即为物质点。这种方法的优势在于能精确地描述物质运动边界且计算效率高,同时可以获得材料的应力时程。数值计算中采用单点高斯积分单元,并引入沙漏黏性阻力以控制零能模态。
3.1.1 材料模型与参数
采用高能炸药燃烧模型和Jones-Wilkins-Lee (JWL)状态方程描述炸药的爆燃过程,状态方程描述了爆轰产物的压力,相对体积和爆轰产物比内能0的关系[15]:
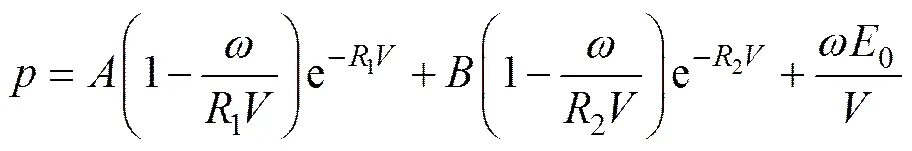
式中:,,1,2和均为材料输入参数,炸药的材料模型及状态方程参数如表2所示[16]。

表2 炸药的材料模型及状态方程参数
注:e为炸药密度;D为爆轰速度;CJ为C-J压力。
通过评价LS-DYNA土体材料库,MAT 147适合描述完全饱和砂土的性状[17]。该模型采用修正的莫尔−库仑屈服面以避免低应力时屈服面与静水压力轴交汇的奇异点,如图4所示。
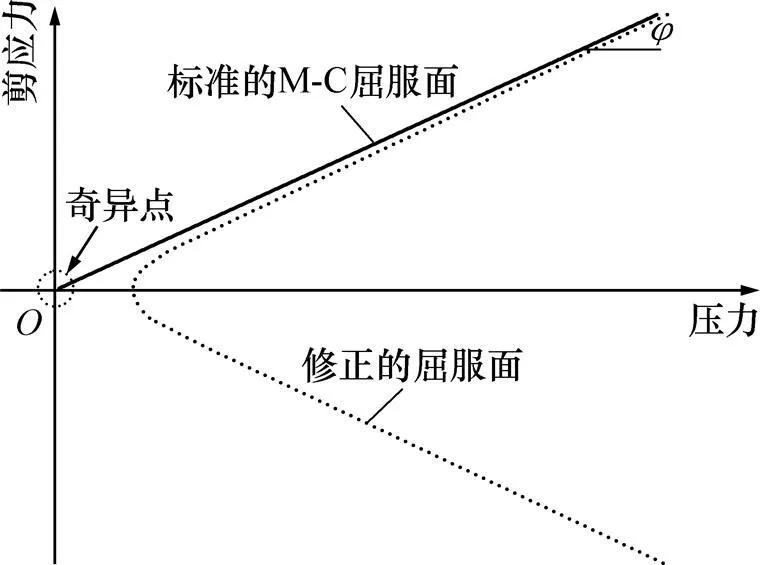
图4 MAT147模型的修正屈服面
该模型以含水量作用于体积模量的关系式来描述孔隙水压力与体积压缩应变的关系:
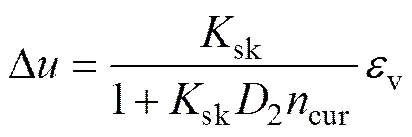
式中:sk为体积应变因子(孔隙水压力系数),为不含气体孔隙的土体体积模量;v为总体积应变;2为气体孔隙坍塌前控制孔隙水压力的材料常数,对于饱和砂土,其对孔隙水压力变化的影响可以忽略[17]。
根据试验砂土物理力学性质及文献给出饱和砂土的计算参数[17−18],如表3所示。饱和黏土的饱和容重为21.5 KN/m3,土粒相对密度为2.7,体积模量为 120 MPa,剪切模量为30 MPa,内摩擦角为35°,黏聚力为20 kPa,含水率为26.5%,孔压系数sk=0,即不考虑孔压的发展。
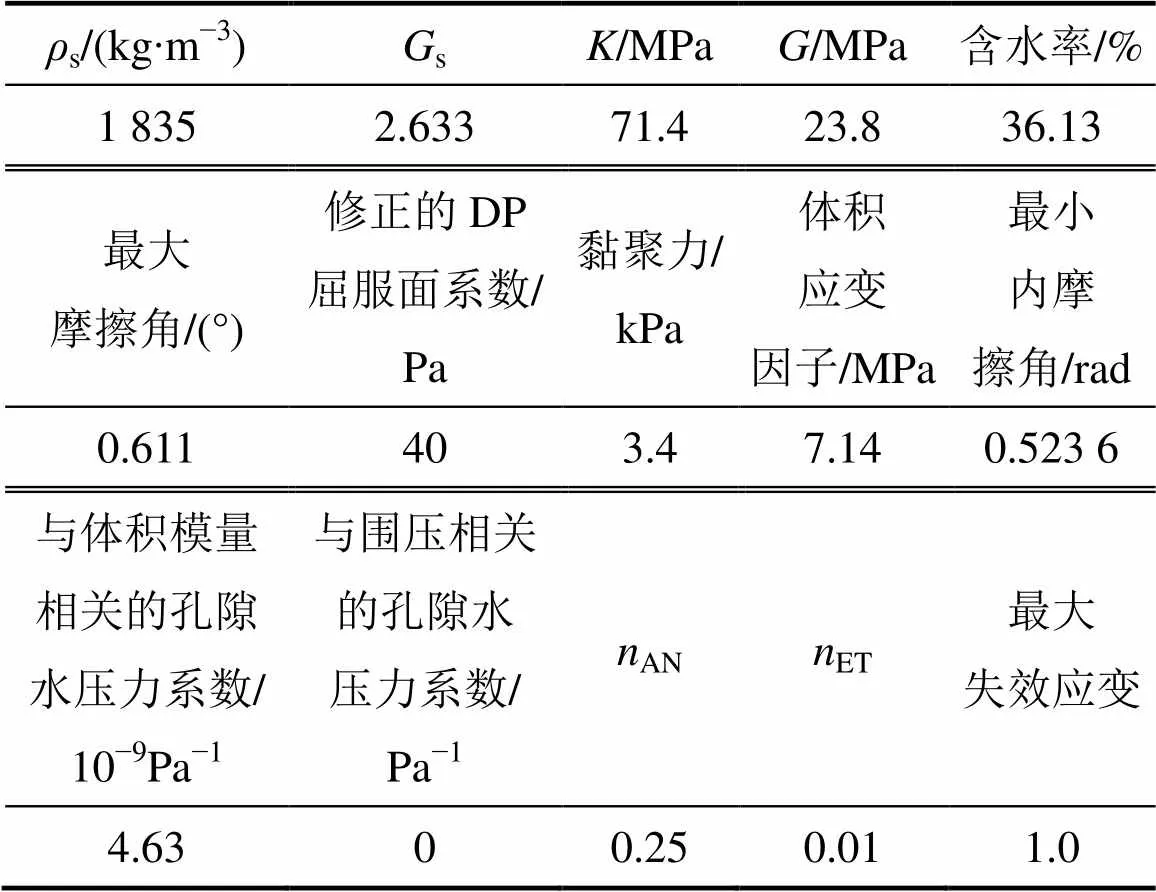
表3 饱和砂土材料参数
s为饱和砂土密度;s为土粒相对密度;和分别为土体的体积模量和剪切模量;AN和ET为应变硬化参数。
3.1.2 数值计算模型
数值模型的计算域直径为16 m,深度4 m,其中0~3 m为饱和砂土层,3~4 m为饱和黏土层。集中药包设置为六棱柱形,每个装药质量为0.6 kg,如图5所示。数值模型上表面为土体与空气接触的自由面,在模型四周定义无反射边界,底部全约束。数值计算第一步利用动态松弛技术进行模型的初始地应力平衡,作为爆炸动力计算的预加载。数值计算有限元模型及应力初始化后的几何模型如图5所示。药包周围对有限元网格进行加密,单元最小宽度为0.05 m,初始时间步长为7.15×10−6s。
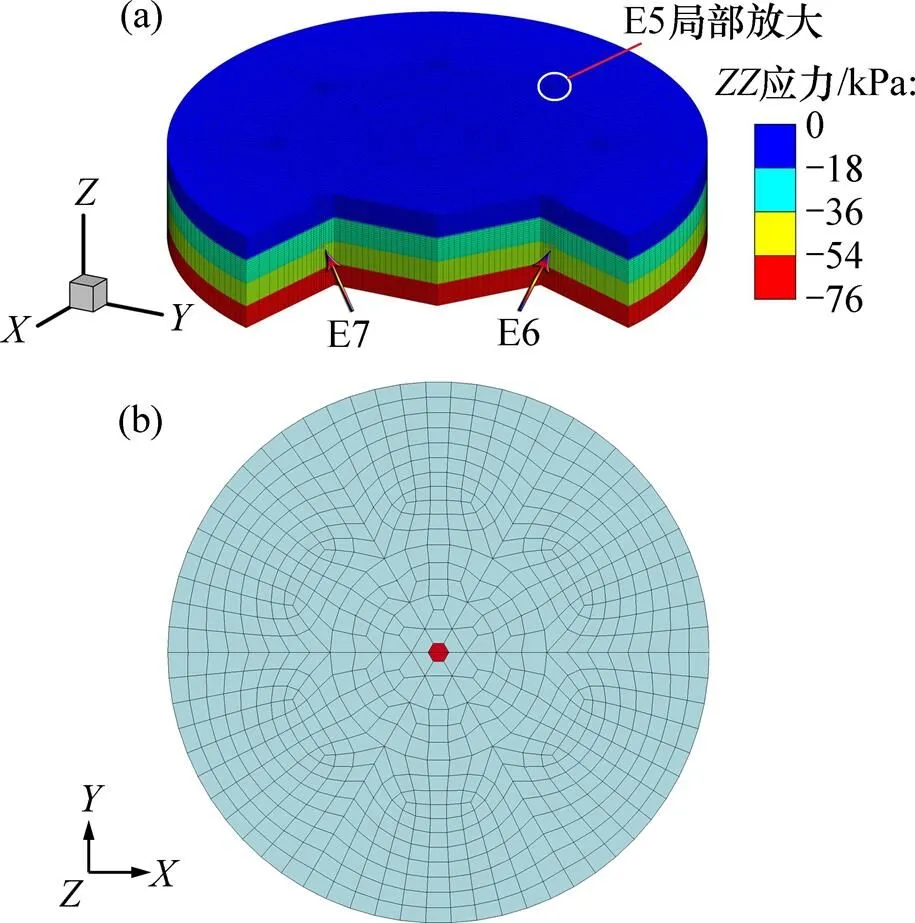
(a) 数值计算有限元模型;(b) 模型局部放大
3.2 试验与数值计算的对比分析
根据试验中孔隙水压力监测点的位置,分别提取计算模型中P1,P5和P8位置处的超孔隙水压力时程,如图6所示。计算得到的超孔隙水压力时程曲线的整体发展规律与试验结果基本一致,试验实测的超孔隙水压力时程曲线在爆后上升阶段具有多个孔压峰值,且超孔隙水压力的累积过程持续时间较长。引起此现象的原因可能有:
1) 试验中监测元件孔内的回填砂土不够密实,导致爆炸应力波在孔内来回传播;
2) 孔隙水压力传感器的灵敏性对孔隙水压力的激发产生影响;
3) 试验坑侧壁和底部为高强度的黏土,饱和后与砂土的阻抗不完全一致,最终可能导致爆炸波在坑壁和坑底发生来回反射和叠加,而数值计算中并未考虑全部因素,这也可能是导致最终计算结果稍小于试验的因素之一。
然而,在分析饱和砂土中孔隙水压力或液化特性时,主要关心孔隙水压力峰值过后的累积值。由图6可知:数值计算与实测的孔隙水压力累积值相关性较好,表明了全耦合数值模型在描述饱和砂土中的爆炸液化问题的合理性和有效性。
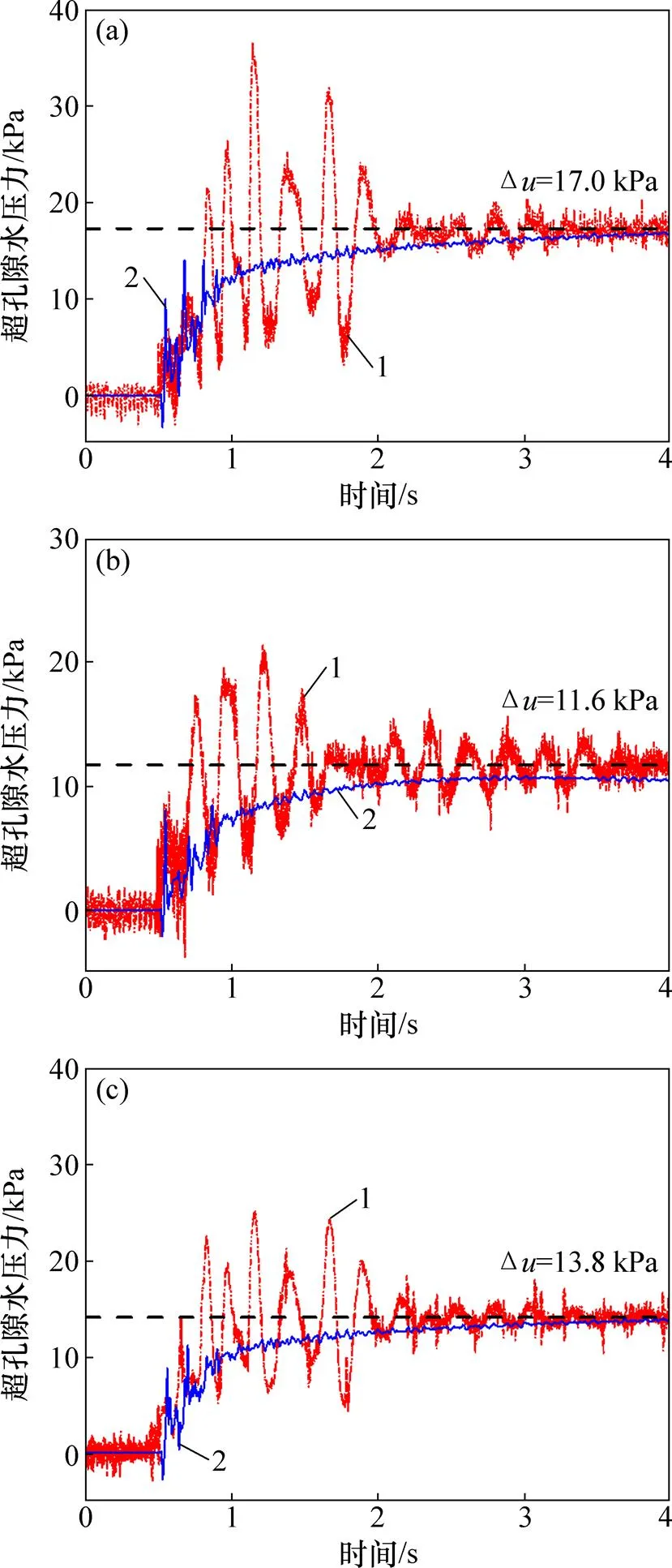
(a) 监测点P1;(b) 监测点P5;(c) 监测点P8
4 爆炸液化特性分析
4.1 超孔隙水压力比分析
在数值模型的药包埋设深度平面上沿着线A选取一系列示踪单元(图1),提取体积应变并得到超孔隙水压力在比例距离半对数坐标中的变化关系,如图7所示,图中同时给出了试验中孔隙水压力传感器处的实测超孔隙水压力比以及预测饱和砂土场地爆炸液化的STUDER(1980)[5]和ROLLINS(2005)[2]经验公式。其中,应用最广泛的Studer经验公式仅适用于单药包的液化预测,未考虑多药包的孔隙水压力累积效应,因此,超孔隙水压力明显小于预测值。Rollins经验公式简化了多药包爆炸液化的众多影响因素,能较好地反映多药包爆炸引起的超孔隙水压力比随比例距离的关系。因此,根据该基本型式及数值计算得到的超孔隙水压力比,建立适用于此条件下的经验公式:
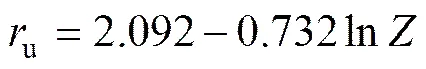
4.2 爆炸液化影响因素分析
4.2.1 爆炸延时影响分析
试验中各相邻药包的起爆间隔时间设置为110 ms,在上述计算模型基础上,将爆炸延时Δ分别设置为220,330,440和550 ms,以评价多点爆炸延时对液化效应的影响。孔隙水压力示踪点包括P5,P8以及点B(位于线A上,深度为2 m,比例距离为7.09 m/kg1/3,见图8)。
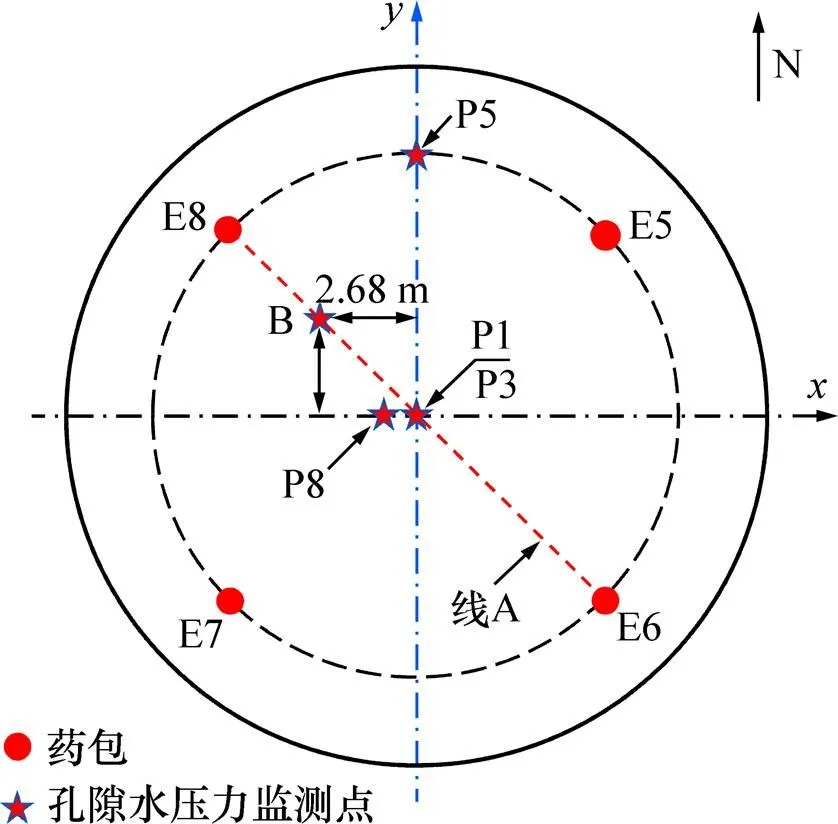
图8 药包及示踪点设计
图9所示为各示踪点处的超孔隙水压力随爆炸延时的变化关系曲线。由图9可知:当爆炸延时从110 ms增大至330 ms时,爆炸引起的饱和土中超孔隙水压力呈快速增大的趋势。其中对于靠近场地中心的示踪点P8处的超孔隙水压力增长接近20%;当爆炸延时超过330 ms时,其对土中累积超孔隙水压力的影响逐渐减弱。分析不同位置示踪点处的最大超孔隙水压力累积值,场地中心区域的示踪点更易受爆炸延时改变的影响。这是因为规则布置的各药包爆后形成的爆炸波在场地中心区域更容易发生爆炸波的叠加效应,如图10所示。图10中仅给出了药包埋置深度截面上炸药顺序起爆后的爆炸波传播云图,输出时间间隔均为0.01 s。由图10可知,E5药包起爆后爆炸波在平面内从药包中心处开始以圆形扩张。至药包E6和E7爆后0.03 s时,可以观测到明显的爆炸波叠加现象。
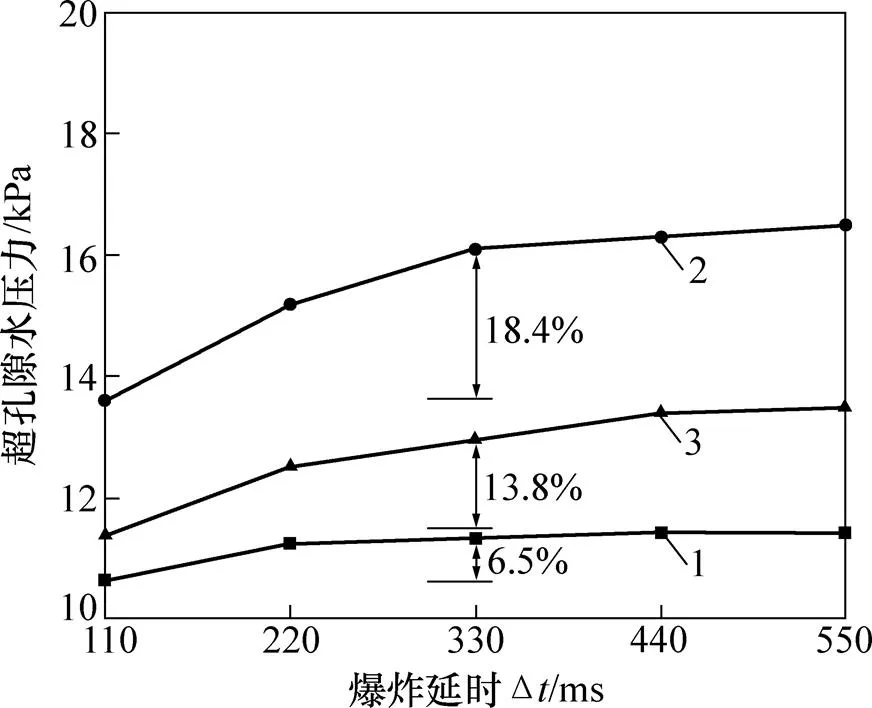
1—示踪点P5;2—示踪点P8;3—B点。

(a) 爆点E5;(b) 爆点E6;(c) 爆点E7
4.2.2 药包质量影响分析
为分析药包总质量对土中超孔隙水压力上升的影响,共设计5组对比数值试验,如图8和表4所示。选取场地中心深度为2 m的单元为示踪点,图11所示为不同爆炸工况下示踪点处获得的超孔隙水压力时程曲线的对比。
由图11可知,超孔隙水压力随着总药量的增加明显增加,但增长趋势逐渐减小:工况4和5之间的超孔隙水压力增量仅为工况1和2之间增量的65%,工况2和4之间增量的80%。分析工况2和3,相同药包仅改变位置(保持比例距离不变)条件下超孔隙水压力的差别基本可以忽略。
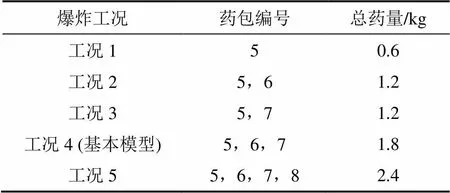
表4 药包质量影响分析爆炸工况
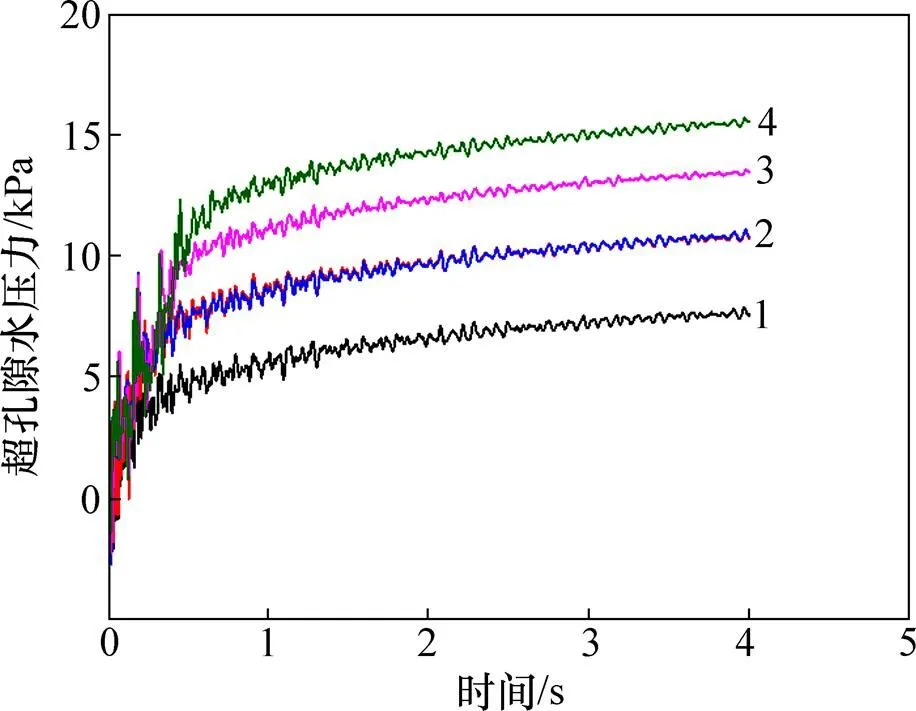
1—工况1;2—工况2/工况3;3—工况4;4—工况5。
5 结论
1) 饱和砂土场地多点微差爆炸液化全耦合数值模型可以较好地反映爆炸峰值过后超孔隙水压力的累积过程,数值计算得到的超孔隙水压力时程曲线的整体发展规律与试验结果基本一致,验证了全耦合数值模型在描述饱和砂土中的爆炸液化问题的合理性和有效性。
2) 基于数值计算得到的超孔隙水压力比,建立了适合该场地条件的多点爆炸液化经验预测公式,能较好地反映超孔隙水压力比随比例距离的关系。
3) 当爆炸延时从110 ms增至330 ms时,爆炸引起的饱和土中超孔隙水压力改变明显,多药包爆炸后在场地几何中心附近更容易形成爆炸波的叠加,从而导致该区域的示踪点更易受爆炸延时改变的影响,计算结果显示优化爆炸延时后场地中心测点处的超孔隙水压力可以提高18%以上。
4) 饱和土中的超孔隙水压力随着总药量的增加明显增加,然而增长趋势逐渐减小;相同药包仅改变位置(保持比例距离不变)条件下超孔隙水压力的差别基本可以忽略。
[1] 李立云, 杜修力. 动载作用下饱和土壤液化的研究述评[J]. 世界地震工程, 2006, 22(6): 39−49. LI Liyun, DU Xiuli. Review on the liquefaction research of saturated soils under dynamic load[J]. World Earthquake Engineering, 2006, 22(6): 39−49.
[2] ROLLINS K M, GERBER T M, LANE J D, et al. Lateral resistance of a full-scale pile group in liquefied sand[J]. Journal of Geotechnical and Geoenvironmental Engineering. 2005, 131(1): 115−125.
[3] AL-QASIMI E M A, CHARLIE W A, WOELLER D J. Canadian liquefaction experiment (CANLEX): Blast-induced ground motion and pore pressure experiments[J]. Geotechnical Testing Journal, 2005, 28(1): 9−21.
[4] 钱七虎, 王明洋. 岩土中的冲击爆炸效应[M]. 北京: 国防工业出版社, 2010: 265−269. QIAN Qihu, WANG Mingyang. Impact and explosion effects in rock and soil[M]. Beijing: National Defense Industry Press, 2010: 265−269.
[5] STUDER J, KOK L. Blast-induced excess porewater pressure and liquefaction experience and application[C]//International Symposium on Soil under Cyclic and Transient Loading, Swansea, UK, 1980: 581−593.
[6] ASHFORD, S A, ROLLINS, K M, LANE J D. Blast-induced liquefaction for full-scale foundation testing[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(8): 798−806.
[7] 王兰民, 何开明, 石玉成, 等. 饱和黄土液化的现场爆破地震动试验研究[C]//第六届全国土动力学学术会议.南京, 2002: 560−565. WANG Lanmin, HE Kaiming, SHI Yucheng, et al. The study on liquefaction of saturated loess by in-situ explosive test[C]//The 6th National Conference on Soil Dynamics. Nanjing, 2002: 560−565.
[8] 张智超, 陈育民, 刘汉龙, 等. 孔隙水压力及炸药埋深对堤坝爆炸效应的影响分析[J]. 岩土力学, 2012, 33(7): 2214−2220. ZHANG Zhichao, CHEN Yumin, LIU Hanlong, et al. Analysis of influences of pore water pressure and buried depth of explosive on blasting effect of embankments[J]. Rock and Soil Mechanics, 2012, 33(7): 2214−2220.
[9] JAYASINGHE L B, THAMBIRATNAM D P, PERERA N, et al. Computer simulation of underground blast response of pile in saturated soil[J]. Computers and Structures, 2013, 120(2): 86−95.
[10] MARCUSON W F. Definition of terms related to liquefaction[J]. Journal of the Geotechnical Engineering, 1978, 104(9): 1197−1120.
[11] LEONG E C, ANAND S, CHEONG H K, et al. Re-examination of peak stress and scaled distance due to ground shock[J]. International Journal of Impact Engineering, 2007, 34(9): 1487−1499.
[12] WANG P, XEI X A, HE W D. Preparation and performance of a novel water gel explosive containing expired propellant grains[J]. Central European Journal of Energetic Materials, 2013, 10(4): 495−507.
[13] 施鹏, 辛凯, 杨秀敏, 等. 土中装药不同埋深爆炸试验研究[J]. 工程力学, 2006, 23(12): 171−174. SHI Peng, XIN Kai, YANG Xiumin, et al. Experimental study of explosion with different burial depths in soil[J]. Engineering Mechanics, 2006, 23(12): 171−174.
[14] 穆朝民, 任辉启, 李永池, 等. 变埋深条件下饱和土爆炸能量耦合系数的试验研究[J]. 岩土力学, 2010, 31(5): 1574−1578. MU Chaomin, REN Huiqi, LI Yongchi, et al. Experiment study of explosion energy coupling coefficient with different burial depths in saturated soils[J]. Rock and Soil Mechanics, 2010, 31(5): 1574−1578.
[15] Livermore Software Technology Corporation, Inc. LS-DYNA Keyword User's Manual, Version 971/R5[M]. California: Livermore Software Technology Corporation Inc, 2010: 66−68.
[16] 刘红岩, 王新生. 地表垂直爆破震动速度的数值计算[J]. 爆炸与冲击, 2008, 28(3): 265−270. LIU Hongyan, WANG Xinsheng. Numerical calculation of ground vertical blasting vibration velocity[J]. Explosion and Shock Waves, 2008, 28(3): 265−270.
[17] LEWIS B A. Manual for LS-DYNA soil material model 147[R]. McLean, VA: Federal Highway Administration Research, Turner-Fairbank Highway Research Center, 2004: 9−21.
[18] LEE W Y. Numerical modeling of blast induced liquefaction[D]. Utah: Brigham Young University. Department of Civil and Environmental Engineering, 2006: 91−98.
(编辑 赵俊)
Experimental and numerical investigations of liquefaction in saturated sand during multiple blasts with milliseconds interval
YAO Yingkang1, 2, WANG Weiguo2, JIA Yongsheng1, CHEN Yumin2
(1. Wuhan Municipal Construction Group Co. Ltd., Wuhan 430023, China;2. College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China)
A fully coupled numerical model was set up and validated by the data from a multiple-blast liquefaction test. The influence of detonation delay and charge mass on excess porewater pressure was analyzed. The results show that the empirical equation established from the numerical results is a good way to describe the relationship between excess porewater pressure ratio and scaled distance. Excess porewater pressure increase can be up to 18% on the center area of the test pit when the detonation delay changes from 110 ms to 330 ms due to the superposition effect of blast waves. Excess porewater pressure increases with the increase of charge mass obviously, while the growth trend decreases gradually.
saturated sand; multiple blasts with milliseconds delay; blast-induced liquefaction; excess porewater pressure; numerical simulation
10.11817/j.issn.1672−7207.2017.06.028
TU 437
A
1672−7207(2017)06−1621−08
2016−06−17;
2016−07−23
国家自然科学基金资助项目(51379067);长江学者和创新团队发展计划(IRT1125)(Project(51379067) supported by the National Natural Science Foundation of China; Project(IRT1125) supported by Program for Changjiang Scholars and Innovative Research Team in University)
王维国,博士,从事土体爆炸动力响应方面的研究,E-mail:2008hmily@163.com
