基于改进果蝇优化算法的人群疏散仿真

张 超, 梁西陈, 魏三强,2

(1.宿州职业技术学院计算机信息系,安徽宿州234101;2.中国矿业大学信息与控制工程学院,江苏徐州221116)

基于改进果蝇优化算法的人群疏散仿真

张 超1, 梁西陈1, 魏三强1,2

(1.宿州职业技术学院计算机信息系,安徽宿州234101;2.中国矿业大学信息与控制工程学院,江苏徐州221116)

基本果蝇优化算法收敛精度不高,易陷入局部极值,在人群疏散仿真中存在疏散路径不平滑的缺陷。为此,借鉴萤火虫算法思想,赋予果蝇个体感知域,在感知域内有邻居时,向邻居集合内味道浓度最佳的果蝇个体飞去,没有邻居时,向果蝇群体味道浓度最佳的个体飞去。向邻居集合最优个体学习时,为了防止算法陷入局部最优,采用局部极值和全局极值相结合的动态位置搜索方式。迭代开始阶段果蝇个体主要向局部极值方向飞去,以便获得多个极值点。随着迭代次数增加,果蝇群体极值所占比重逐渐增加,在确保求解精度的同时提高收敛速度。将改进的算法在4个经典测试函数上进行性能分析,实验结果表明,改进的算法在收敛速度,特别在收敛精度上有显著提高。将改进的算法应用在双出口房间人群疏散仿真中,实现了疏散路径平滑、疏散仿真度较好的效果。

果蝇优化算法;人群疏散仿真;萤火虫算法;智能算法;群体动画

0 引言

随着经济社会的发展和城市化进程的加快,大型购物商场、广场、影院、火车站等公共场所人员流动量大容易造成紧急突发事件,在突发事件发生时如何以最快的速度将大量人员疏散到安全的地点成为学者们研究的热点问题[1]。各种疏散模型被相继提出并应用在人群疏散仿真中,如元胞自动机模型[2]、Agent模型[3-4]、基于密度模型[5]、格子气模型[6]、社会力模型、离心力模型[7]等。目前已有的疏散模型主要可分为宏观和微观两大类。宏观模型以人群整体为研究对象,不考虑人群个体之间的交互和影响,大多通过流体力学理论、动态网络均衡理论、路径选择模型对密集人群的流体运动过程和路径选择行为进行刻画,仿真度较差[8]。微观模型充分考虑个体行为特征和个体之间的差异,以人群个体行为作为研究对象,成为人群疏散研究的热点,如文献[2-6],但也存在计算量大、运算速度慢等缺点。

群体智能算法是对自然界生物群体涌现现象的仿生设计,有着其他模型无法比拟的优点,能够实现个体之间的信息交互及自组织特性,被广泛应用于函数优化、组合优化、生产调度问题、自动控制、机器学习、图像处理等领域[9-11]。鉴于群体智能算法在模拟群体行为特征上的优点,近年来,学者们相继开展群体智能算法在人群疏散仿真领域的研究。万江华等[12]对标准粒子群算法的惯性权重进行优化,加入了影响力因子,很好地模拟了突发事件中的领导者行为;张鹏等[13]提出一种基于种群划分思想的新型蜂群算法,实现了人群疏散的均衡分布,提高了应急疏散的效率;晁素娜等[14]将改进的萤火虫算法应用在人群疏散仿真中,提高了疏散路径的平滑性和稳定性。因此,将群体智能算法应用到人群疏散仿真中能够为人群疏散领域的研究提供新的方法。果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)[15]是一种新型的群体智能算法,因其算法原理简单、参数少、实时性好,现已被广泛应用于神经网络优化、工业设计等科学和工程领域[16-17]。为此,本文提出将果蝇优化算法应用到人群疏散仿真中,为人群疏散仿真研究提供一种新的思路。

人群的应急疏散过程是人的个体移动行为、路径选择行为和群体博弈行为共同作用的结果。人在紧急事件中往往表现出恐慌、亲和和从众的心理特征。在应急疏散中表现为向人多的地方靠拢或跟随最近的逃生者移动,应急疏散中的人总是希望以最快的速度到达安全区域,这与果蝇优化算法中果蝇群体总是向离食物源近的味道浓度最高的果蝇飞去有着类似的行为选择特征。因此,将果蝇优化算法应用到人群疏散仿真中在理论上是可行的。但基本果蝇优化算法中在算法的每次迭代过程中所有果蝇都飞向群体中味道浓度最高的个体,依赖全局信息引导果蝇进行位置搜索,缺乏局部信息的搜索,这种机制降低了种群的多样性,极易使算法陷入局部最优而无法跳出局部极值[18],导致在人群疏散仿真时疏散路径不够平滑。

针对基本果蝇优化算法在人群疏散仿真时疏散路径不够平滑的缺陷,本文参考萤火虫算法(Glowworm Swarm Optimization,GSO)[19],将局部极值加入到果蝇的位置更新中,以扩展群体的多样性,增加局部极值点。当前果蝇个体在可视范围内有邻居时,向邻居集合中味道浓度最优(局部极值)的个体飞去,模拟人群在紧急疏散时总是向离自己最近的逃生者移动的行为特征;当前个体没有邻居时,向果蝇群体味道浓度最优(全局极值)的个体飞去。向邻居集合最优个体学习时,为了防止算法陷入局部最优,采用局部极值和全局极值相结合的动态位置搜索方式。迭代寻优开始阶段果蝇个体主要向局部极值方向飞去,以便获得多个极值点。随着迭代次数的增加,果蝇群体极值所占比重逐渐增加,从而确保求解精度的同时提高收敛速度。将改进的算法在4个常用的经典测试函数上进行性能分析,实验结果表明,改进的算法在收敛速度和精度上均有显著提高。将改进的果蝇优化算法应用在人群疏散仿真中实现了疏散路径平滑、疏散仿真度较好的效果。

1 果蝇优化算法

2011年,潘文超[16]根据果蝇觅食的群体特征提出了果蝇优化算法。吴小文等[20]将果蝇优化算法与遗传算法、蚁群算法、鱼群算法,免疫算法、粒子群算法等5种算法在Schaffer函数上进行性能分析对比实验,得出FOA具有算法简单、易于实现、较容易应用于解决实际问题。近年来,果蝇优化算法已被广泛应用于科学和工程等领域。

1.1 果蝇优化算法基本原理[17]

果蝇具有敏锐的嗅觉和视觉器官,可以嗅到距离达40 km以外的食物源散发的气味,飞近食物后利用敏锐的视觉能够发现食物和同伴聚集的位置,并迅速向该位置飞去。

根据果蝇觅食的特点,FOA可以归纳为如下步骤:

(1)设置种群规模sizepop和最大迭代次数maxgen(或目标精度),随机初始化果蝇群体位置坐标(X,Y)

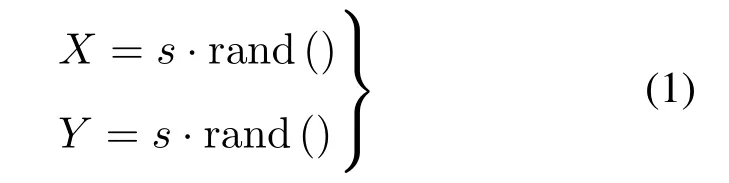
式中:s为可调参数;rand()是介于0～1的随机数。

(2)赋予果蝇个体利用嗅觉搜索食物的随机方向(RandomValue)和位置(X(i),Y(i))

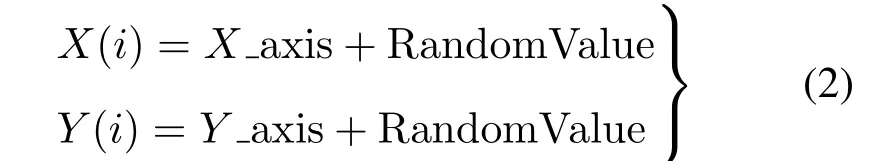
(3)由于无法准确获知食物源的位置,先估算每个果蝇个体与原点之间的距离d,再取其倒数作为果蝇个体i的味道浓度判定值S(i)

(4)将果蝇个体i的味道浓度判定值代入味道浓度判定函数(类似适应度函数Fitness),求出每个果蝇个体所处位置的味道浓度Smell(i)。

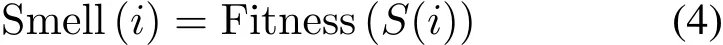
(5)根据初始味道浓度值寻找果蝇群体初始极值(极大或极小值)

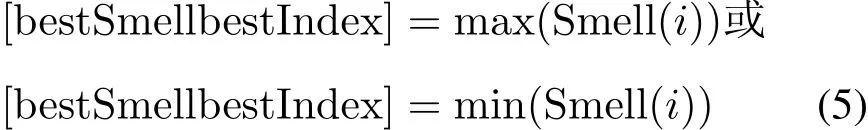
(6)存储果蝇群体最佳味道浓度值及其对应的位置坐标(X,Y),这时果蝇群体利用视觉向该位置飞去

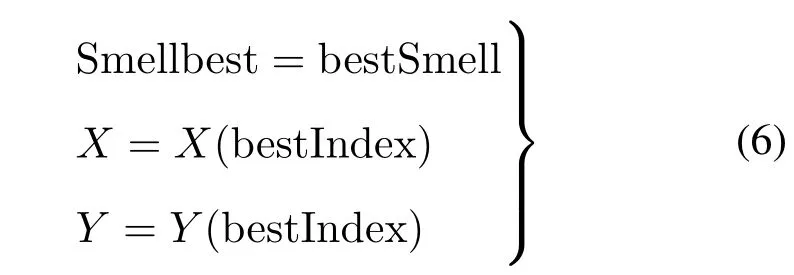
(7)进入迭代寻优,重复执行步骤(2)～(5),并判断味道浓度是否优于前一迭代味道浓度,若是,执行步骤(6);否则,返回步骤(2),直至满足最大迭代次数或设定精度,算法停止。

1.2 改进的果蝇优化算法

1.2.1 算法的改进设计

在FOA算法的每次迭代过程中,所有果蝇都飞向群体中味道浓度最高的个体,依赖全局信息引导果蝇进行位置搜索,缺乏局部信息的搜索,这种机制降低了种群的多样性,极易使算法陷入局部最优而无法跳出局部极值,导致算法收敛精度不高,在人群疏散仿真时导致疏散路径不够平滑。在FOA算法中当前迭代味道浓度最优的个体是通过果蝇个体所处位置与原点距离之倒数估算而来,未必是全局最优。为此,参考萤火虫算法,为果蝇个体设置感知域,将局部极值加入到果蝇个体的位置更新中,以扩展群体的多样性。当前果蝇个体在感知域内有邻居时,向邻居集合中味道浓度最优(局部极值)的个体学习;没有邻居时,向果蝇群体味道浓度最优(全局极值)的个体学习。向邻居集合最优个体学习时,为了防止算法陷入局部最优,采用局部极值和全局极值相结合的动态位置搜索方式。迭代寻优开始阶段果蝇个体主要向局部极值方向飞去,以便获得多个极值点。随着迭代次数的增加,果蝇群体极值所占比重增加,从而确保求解精度的同时提高收敛速度。改进算法记为GFOA(G lowworm Fruit Fly Optimization Algorithm)。

果蝇按下式获取邻居集合:

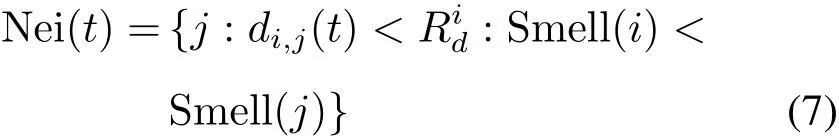
式中:Nei(t)是果蝇i第t次迭代时的邻居集合,j∈Nei(t);di,j(t)是果蝇i和j第t次迭代时的欧式距离;Rid是果蝇i的感知域;Smell(i)、Smell(j)是果蝇i和j在第t次迭代时所处位置的味道浓度。

果蝇按下式动态调整感知域,

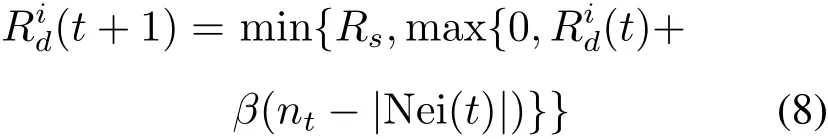
邻居集合密度高就缩小感知范围;反之,增加。

式中:nt为常数;邻居数的上限;β为感知域更新率。

如果果蝇i在当前迭代时邻居集合为空,按式(2)的随机方向和位置搜寻食物。否则,按下式的局部极值和全局极值相结合的动态位置搜寻食物:

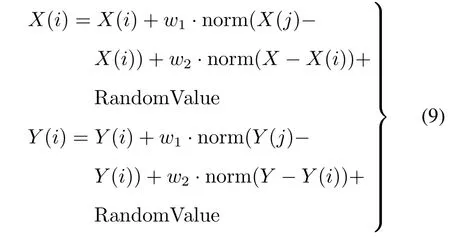
式中,X(j)、Y(j)为局部最优果蝇个体所处位置。

w1和w2的取值范围在[c1,c2]之间,c1、c2的取值范围在[0.6,4]之间,且c1＞ c2。w1随着迭代次数t的增加而线性减少,w2随着迭代次数t的增加而线性增加。基本果蝇算法以上一迭代过程中味道浓度最佳的果蝇个体所处位置,作为下一迭代过程中所有果蝇个体的开始搜索位置。味道浓度最佳果蝇个体所处位置由其距原点距离之倒数估算而来。在4个经典测试函数Schwefelf、Sphere、Griewank、Schaffer上寻找最优值的实验来看,虽能很快收敛,但精度不高,易陷入局部极值。式(9)通过当前个体到局部最优个体和全局最优个体的欧式距离,作为下一迭代的开始搜索位置,该位置将局部最优和全局最优2个因素都加入进来,是个动态调整值,适当提高c1、c2取值,可以扩展果蝇群体多样性和搜索空间,显著提高收敛精度。

1.2.2 GFOA算法的执行流程

基于1.2.1节的改进,GFOA算法的基本步骤如下:

(1)设置种群规模sizepop和最大迭代次数maxgen(或目标精度),根据式(1)为果蝇群体初始化位置坐标。

(2)如果果蝇个体没有邻居,按式(2)设定果蝇个体搜寻食物的方向和距离;否则,按式(9)搜寻食物,并根据式(8)动态调整果蝇感知域。

(3)根据式(3)计算果蝇个体i的味道浓度判定值S(i)。

(4)根据式(4)计算每个果蝇个体初始位置的味道浓度Smell(i)。

(5)根据式(5)计算出果蝇群体初始极值bestSmell(极大或极小值)。

(6)根据式(6)存储果蝇群体依据初始位置计算的最佳味道浓度值Smellbest及其对应的最佳位置坐标(X,Y)。

(7)进入迭代寻优,首先,依据果蝇个体初始位置,按式(7)获取果蝇的邻居集合Nei(t),重复执行步骤(2)～(5),并判断味道浓度是否优于前一迭代味道浓度,若是,执行步骤(6);否则,返回步骤(2),直至满足最大迭代次数或目标精度,算法停止。

2 GFOA算法的性能分析

2.1 实验部署

为了验证GFOA算法的寻优性能,对FOA和GFOA做对比分析实验。从标准函数测试集CEC2005中选取4个经典测试函数,函数的表达式、变量范围、理论极值见表1。在主频2.50 GHz的CPU、4 GB内存、64 bit Win10操作系统的计算机上,使用MatlabR2012a编程实现。

程序参数设置:

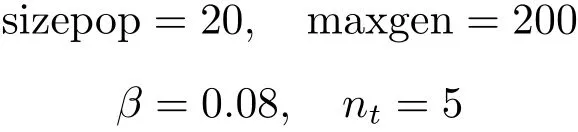
Schwefelf、Sphere、Schaffer函数 s= 100,Griewank 函数 s=300,RandomValue=20·rand()−10,Schwefelf、Sphere、Griewank函数:c1=1.8,c2=0.6,Schaffer函数:c1=4,c2=3。

表1 测试函数Tab.1 Test function

2.2 实验结果与分析

用FOA和GFOA算法分别对表1中4个经典测试函数随机独立连续运行20次,实验结果见表2。从表2中可以看出,对2个单峰函数、2个多峰函数,GFOA算法在最差值、最优值、优化平均值和标准差4个评价指标上均优于FOA算法。图1中,由于GFOA的收敛精度显著优于FOA,故在同一坐标系下味道浓度收敛进化曲线近似为直线,为了便于观察,对Schwefelf、Sphere、Griewank函数的味道浓度取10为底的对数处理,对于Griewank函数,GFOA算法的味道浓度进化曲线出现间断,表示GFOA算法在该函数上已寻找到最优值0,对数的真数为0时不显示。由图1可见,GFOA算法收敛到最优值的速度明显优于FOA。FOA算法在Sphere、Griewank函数上分别有2次陷入局部极值;在Schwefelf函数上有3次陷入局部极值。在Sphere函数上陷入局部极值的寻优结果为:0.007 723、0.008 244。在Griewank上陷入局部极值的寻优结果为:0.001 253,0.001 165。GFOA算法对于强烈震荡的多峰值函数f3、f4,均能快速收敛到函数的理论极值点,对于函数f1、f2,GFOA算法的收敛精度较FOA算法有显著提高。函数f4被认为是最难寻得极值点的函数,其在理论极值周围分布着很多极值点。GFOA算法在函数f4上未陷入“早熟收敛”现象,而使果蝇个体在进化后期停滞不前。

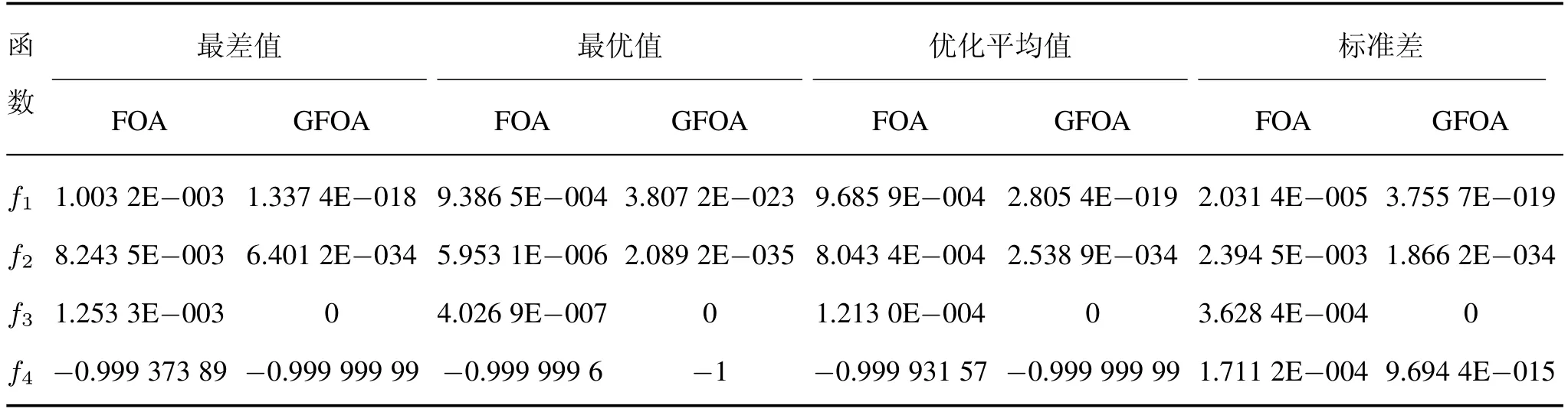
表2 实验结果Tab.2 Experimental results

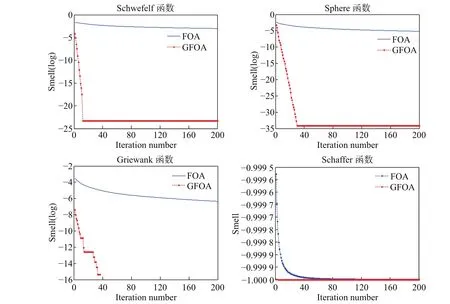
图1 味道浓度收敛趋势图Fig.1 Convergent tendency chart of smell concentration

表3为固定精度下的FOA算法和GFOA算法的平均迭代次数和成功率。其中,Schwefelf、Sphere、Griewank函数的目标精度设为:10−10,Schaffer函数设为:10−10～1。表中实验结果使用“平均迭代次数/成功率”数值格式,其中使用1代表百分之百收敛到目标精度。由表3可知,在较高目标精度下GFOA算法均能百分百成功收敛,而基本FOA算法均不能收敛到固定精度。GFOA算法在4个函数上的平均迭代次数分别为:20.15,12.1,13.3,12.3,说明改进的算法有效提高了算法的收敛速度。

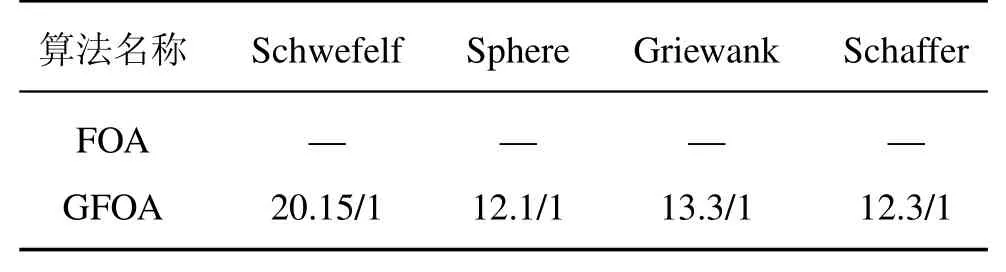
表3 固定精度下平均迭代次数与成功率Tab.3 Number of iterationsand success rate under fi xed precision

3 基于GFOA的人群疏散仿真方法

人群在应急疏散中的行为总是呈现向人多的地方靠拢或跟随最近的逃生者移动,并伴随复杂的自组织现象产生。人群在应急疏散中所涌现的群体特性与觅食中的果蝇群体有着类似的行为选择特征。果蝇总是向味道浓度高的离食物源近的果蝇飞去,而应急疏散中的人总是希望以最快的速度到达安全区域。GFOA算法赋予果蝇个体感知范围,在觅食过程中优先向自己视线范围内的味道浓度高的果蝇飞去,而应急疏散中的人也拥有自己的视野,会根据实际情况判断选择最佳逃生路线。因此,使用改进的果蝇优化算法引导人群疏散仿真能够获得良好的疏散效果。

3.1 双出口教室人群疏散仿真方案

选定双出口教室作为人群疏散仿真场景。在房间内随机初始化N个果蝇(粒子),果蝇味道浓度与果蝇个体和房间出口距离成反比(将此作为GFOA算法的适应度函数Fitness),距离出口越近,味道浓度越浓。果蝇群体依据与房间2个出口的距离长短选择从哪个出口逃生。这样,果蝇群体按照与出口的距离划分为2个区块。每个区块内的果蝇按照GFOA算法搜索出口,当其视野范围内有邻居时,向邻居集合中疏散位置最佳的果蝇移动,没有邻居时,向区块内疏散位置最佳的果蝇移动,直至所有果蝇都到达安全出口。

使用Flash Develop+Action Script3.0开发仿真程序。人群在疏散过程中能够自动避开障碍物。为此,在仿真程序中添加碰撞检测和避免算法,以实现具有真实感行为的仿真效果。仿真程序选用层次包围盒和欧式距离相结合的碰撞检测和避免算法[21]。该算法能够实现人群在疏散过程中自动避开教室内的课桌等障碍物,并防止与墙壁产生穿插现象。

3.2 仿真结果与分析

将果蝇种群规模设定为40,随机进行一次疏散仿真实验,图2截取了疏散仿真程序运行时的3种状态。图2(a)为果蝇初始分布状态,图2(b)为疏散中期果蝇分布状态,图2(c)为疏散即将完成时的状态。图2中标记1和2的为出口安全区域,课桌被包围在层次包围盒(圆)中。图2(b)显示,果蝇群体按照与出口距离长短划分为2个区块进行疏散,果蝇在各自区块内依据GFOA算法搜索邻居集合的最优果蝇或全局最优果蝇,并跟随该果蝇移动疏散。由于添加了碰撞检测和避免算法,果蝇在疏散过程中能够自动避开包围在层次包围盒(圆)中的课桌,防止了与教室墙壁的穿插。由图2(c)可见,果蝇陆续到达安全区域,即将完成疏散。图3是GFOA算法和FOA算法生成的疏散路径曲线对比图,从图中可知,FOA算法生成的疏散路径曲线不光滑,特别在疏散中后期,果蝇个体都向全局最优位置靠近,造成疏散路径出现跳跃,从而导致在进行人群疏散仿真时的仿真度不高,而GFOA算法生成的疏散路径曲线平稳光滑,说明GFOA算法使用局部最优和全局最优相结合的动态位置更新方式,有效提高了人群疏散的仿真度。如图2(a)所示,仿真程序设计了开始和停止疏散功能,有利于观察分析疏散仿真过程。仿真程序设计了路径导出功能,可以将果蝇个体的疏散路径数据导出,使用MAYA的路径动画技术制作人群仿真动画。

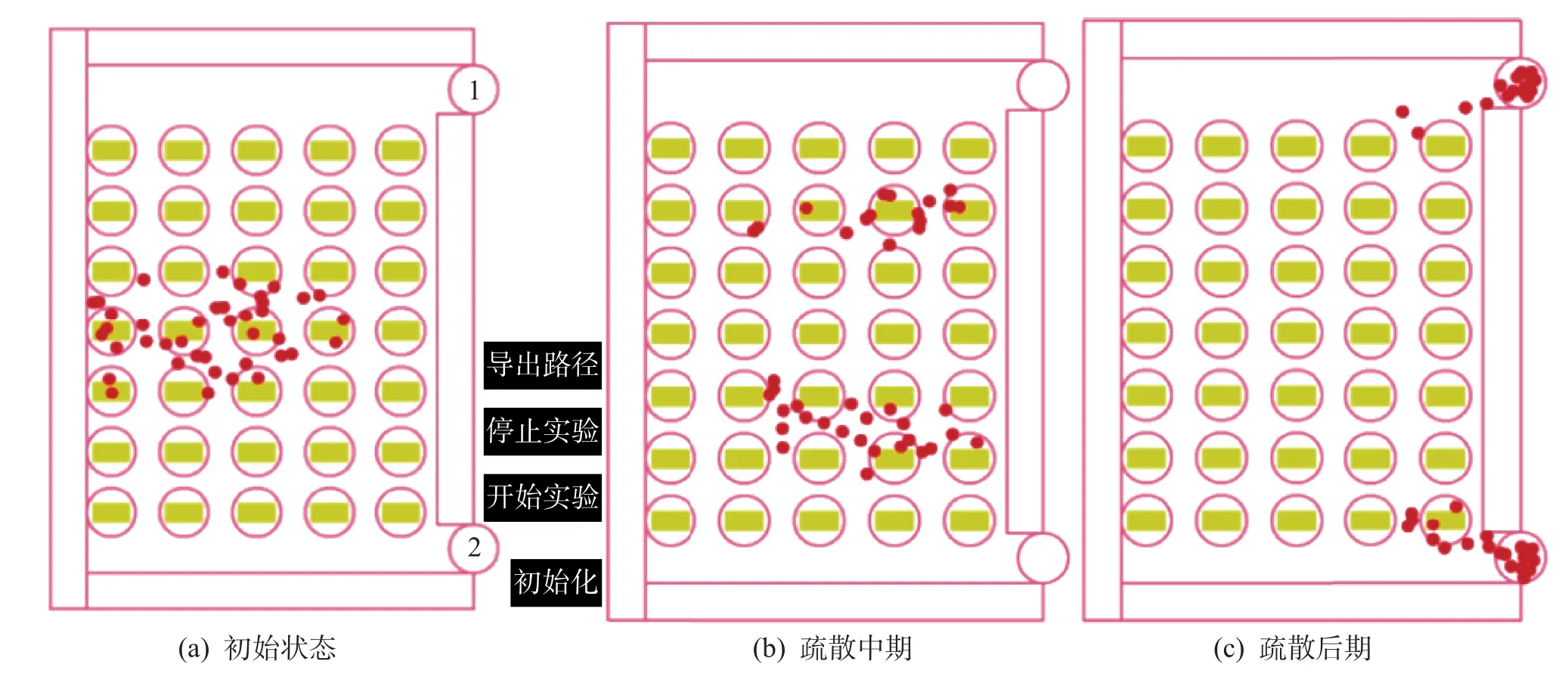
图2 双出口教室人群疏散仿真状态图Fig.2 Statediagram of crowd evacuation simulation from aclassroom with two exits

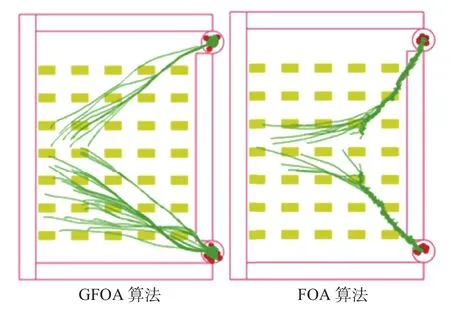
图3 GFOA算法和FOA算法生成的疏散路径曲线图Fig.3 Evacuation path map generated by GFOA algorithm and FOA algorithm

综上所述,使用GFOA算法能够完成双出口房间的人群疏散,且获得了光滑平稳的疏散路径。

4 结语

本文提出将果蝇优化算法应用到人群疏散仿真的研究中,为人群疏散仿真研究提供一种新的思路。

针对果蝇优化算法收敛精度不高、易陷入局部最优、在应用到人群疏散仿真中存在疏散路径不平滑的缺陷,提出了一种改进的果蝇优化算法,并在4个经典测试函数上做了性能分析实验。实验结果表明,

改进的算法在收敛速度、特别在收敛精度上有显著提升。将改进的算法应用在双出口房间人群疏散仿真中,获得了疏散路径平滑、仿真度较好的疏散效果,具有良好的实际应用参考价值。

[1] 吴双,刘弘.人群疏散的社会力蚁群模型[J].山东师范大学学报:自然科学版,2016,31(3):15-20.

[2] 贾斌,高自友,李克平,等.基于元胞自动机的交通系统建模与模拟[M].北京:科学出版社,2007.

[3] ZHONG J H,CAI W T,LUO L B,et al.Ea-based evacuation planning using agent based crowd simulation[C]//TOLI A,DIALLO S Y,RYZHOV I O,et al.Simulation Conference(WSC).Piscataway,NJ,USA:IEEE,2014:395-406.

[4] 陈佳俊,安晓宇,蔡希辉,等.基于Agent的人员疏散系统设计与实现[J].计算机工程,2010,36(14):264-266.

[5] ZHONGJH,HU N,CAIWT,et al.Density-based evolutionary framework for crowd model calibration[J].Journal of Computational Science,2015(6):11-22.

[6] 郭细伟,陈建桥,魏俊红.格子气模型在地铁站人群疏散运动中的应用[J].武汉理工大学学报(交通科学与工程版),2014,38(3):567-571.

[7]CHRAIBI M,SEYFRIED A,SCHADSCHNEIDER A.Generalized centrifugal-forcemodel for pedestrian dynamics[J].Physical Review E Statistical Nonlinear and Soft Matter Physics,2010,82(4):046111.

[8] 禹尔东,吴正,郭明旻.双出口房间人群疏散的实验研究和数学建模[J].物理学报,2014,63(9):094501.

[9] 周永权,黄正新.求解TSP的人工萤火虫群优化算法[J].控制与决策,2012,27(12):1816-1821.

[10]唐海波,叶春明.仿生群智能算法在生产调度中的应用综述[J].工业工程,2010,13(3):1-5.

[11]陈志国,傅毅,孙俊.群体智能算法的遥感图像处理研究[J].计算机应用研究,2013,30(8):2538-2540.

[12]万江华,卜凡亮.粒子群算法在应急疏散中的应用研究[J].中国人民公安大学学报(自然科学版),2011,17(3):59-64.

[13]张鹏,刘弘,王爱霖.基于人工蜂群算法的疏散运动仿真[J].计算机工程,2013,39(7):261-264.

[14]晁素娜,刘弘,张鹏.基于改进萤火虫算法的人群疏散仿真[J].山东师范大学学报(自然科学版),2015,30(1):33-37.

[15]PAN W T.A new fruit fl y optimization algorithm:Taking thefi nancial distressmodel asan example[J]．Knowledge-Based Systems,2012,26(2):69-74．

[16]潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报(社会科学版),2011,29(4):1-5

[17]姚勇涛,吴雪,吴喆.基于改进的果蝇优化算法的WSN节点部署设计[J].华东理工大学学报(自然科学版),2016,42(4):545-551.

[18]徐富强,陶有田,吕洪升.一种改进的果蝇优化算法[J].苏州大学学报(自然科学版),2014,29(1):16-23.

[19]KRISHNANAND K N,GHOSE D.Glowworm swarm optimisation:A new method for optimising multi-modal functions[J].International Journal of Computational Intelligence Studies,2009,1(1):93-119.

[20]吴小文,李擎.果蝇算法和5种群智能算法的寻优性能研究[J].火力与指挥控制,2013,38(4):17-20.

[21]张超.“灵璧三绝”动漫宣传片中的群体动画制作技术[J].江汉大学学报(自然科学版),2015,43(1):58-64.

Abstract:The fruit fl y optimization algorithm has low convergence precision and easily falls into local optimum,which is a weak at smoothness of path in crowd evacuation simulation.Therefore,the perceptual domain which is derived from the glowworm swarm optimization algorithm is given to the individual fruit fl y.If there are neighbors in the perceptual domain of the current fruit fl y,the current fruit fl y to the best smell one in neighbor set,otherwise fl ies to the best smell one which of fruit fl y population.When the fruit fl y learns from the best neighbors,a dynamic location search method based on the combination of local extremum and global extreme value is used to prevent the algorithm from falling into local optimum.At the beginning of the iteration,the fruit fl y fl ies to the local extreme direction to obtain multiple extreme points.With the increase of iteration,the proportion of the global optimal value increases gradually aim to ensure the convergence accuracy and improve the convergence speed.The experimental results of four test functions show that the improved fruit fl y optimization algorithm is signifi cantly improved the algorithm convergence speed and precision.The improved algorithm is applied to the simulation of crowd evacuation in the double exit room.It improves the smoothness of evacuation path and evacuation simulation effect is good.

Keywords:fruit fl y optimization algorithm;crowd evacuation simulation;fi refl y algorithm;intelligencealgorithm;crowd animation

Crowd Evacuation Simulation Based on Improved Fruit Fly Optimization Algorithm

ZHANGChao1,LIANGXichen1,WEISanqiang1,2
(1.Department of Computer Information,Suzhou Vocational and Technological College,Suzhou 234101,Anhui,China;2.School of Information and Control Engineering,China University of Mining and Technology,Xuzhou 221116,Jiangsu,China)

TP 18

A

1001-4543(2017)03-0231-08

10.19570/j.cnki.jsspu.2017.03.012

2017-04-05

张 超(1980–),男,安徽宿州人,讲师,硕士,主要研究方向为智能算法研究、动漫制作技术。E-mail:zc2001888@163.com。

安徽省高校省级自然科学基金重点项目 (KJ2016A781、KJ2016A778),安徽省高校省级质量工程项目(2015jyxm512、2014jxtd065,2015sjjd037),宿州市“551”产业创新团队项目(宿人才2014[2]号)资助