浅谈大学数学研究性学习——一道数学习题的启示

江五元,余天姣

(湖南理工学院 数学学院,湖南 岳阳 414006)

浅谈大学数学研究性学习
——一道数学习题的启示

江五元,余天姣

(湖南理工学院 数学学院,湖南 岳阳 414006)

通过对无穷积分收敛的一道数学习题的解答,探究了无穷积分与无穷级数收敛之间的差异．旨在培养学生研究性学习的能力和勇于探索的精神．

无穷积分; 无穷级数; 收敛; 研究性学习

Abstract: In this paper,we discuss the difference between infinite integral and infinite series convergence by solving a mathematical problem about the convergence of infinite integral.The purpose is to train students' ability of research-oriented learning and the spirit of daring to explore.

Key words: infinite integral,infinite series,convergence,research-oriented learning

前苏联著名教育实践家和教育理论家霍姆林斯基指出: “研究性学习是指学生在教师的指导下,以类似科学研究的方法去获得知识和应用知识的一种学习方式.” 对于地方本科院校来说,培养学生的研究性学习能力十分重要.实际上,很多学生仍然习惯于“学习＝接受＋记忆”的学习模式,因此,学生的学习兴趣不高,主动性不强．在大学阶段的教学过程中,应该让学生转变到“学习＝研究＋创新”的学习模式中来,提高学生解决实际问题的能力,达到人才培养目标.文[2]对大学数学研究性学习的作用进行了调查分析,下面以教材中的一道习题为例来说明研究性学习的过程．

华东师范大学数学系编写的教材《数学分析》(第4版)关于无穷积分的内容中有这样一道习题:

例1[1]试证明: 若f是[a,+∞)上的单调函数,且收敛,则x→+∞.

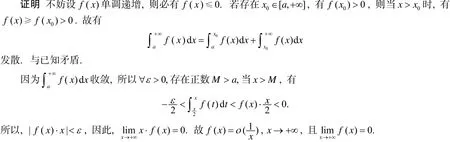
引导学生对这道习题作如下推广:

定理1 若f是[a,+∞)上的单调函数,且收敛,则

注: 当β=0时,即为例1的结论.

例2 讨论的收敛性．

解因为,由狄利克雷判别法可知无穷积分收敛.但显然,极限不存在．

定理2 若f(x)在x∈[a,+∞)上一致连续,且收敛,则.

推论若f(x)在x∈[a,+∞)上有有界的导函数,且收敛,则.

证明由条件可知,∀x∈[a,+∞),∃M＞0,有|f′(x)|≤M．所以由拉格朗日中值定理,∀x1,x2∈[a,+∞),有

所以,f(x)在x∈[a,+∞)上一致连续,由定理2,有．

再由推论,我们可进一步证明[1]中反常积分第1节中的习题:

例3 证明: 若f(x)在x∈[a,+∞)上可导,且都收敛,则.

证明因为收敛,由可积的必要条件,可知f′(x)在x∈[a,+∞)上有界,故由推论1可得．

本文从一道习题出发,通过推广和探究,得到了相应的结论,并利用结论来解决教材中的习题．在这个研究性学习的过程中,学生总结了知识,应用了知识,并挖掘知识点之间的联系与区别．同时,在解决问题的过程中,学生体会到成功的喜悦,从而提高了学生学习的兴趣．

[1]华东师范大学数学系．数学分析 [M].第4版.北京: 高等教育出版社,2010

[2]贺战兵,童咏沙．大学数学研究性学习的现状调查与统计分析[J].长沙铁道学院学报(社会科学版),2006,7(4): 145～146

On Research-oriented Learning of College Mathematics:An Inspiration of a Mathematical Problem

JIANG Wuyuan,YU Tianjiao
(College of Mathematics,Hunan Institute of Science and Technology,Yueyang 414006,China)

G642

A

1672-5298(2017)03-0082-03

2017-01-20

湖南省普通高校教学研究改革项目(湘教通[2015]291号)

江五元(1974− ),男,湖南平江人,博士,湖南理工学院数学学院副教授.主要研究方向: 概率论与数理统计