基于合理低价中标的投标企业非合作博弈论优化模型

张海瑞,李松华,周林林,冯彩英

(1.湖南理工学院 信息与通信工程学院,湖南 岳阳 414006; 2.湖南理工学院 数学学院,湖南 岳阳 414006)

基于合理低价中标的投标企业非合作博弈论优化模型

张海瑞1,李松华2,周林林1,冯彩英1

(1.湖南理工学院 信息与通信工程学院,湖南 岳阳 414006; 2.湖南理工学院 数学学院,湖南 岳阳 414006)

随着电力设备行业竞争进一步加剧,对于投标决策的科学化和实用性要求也越来越高.为提高企业投标的中标率,本文通过引入绩效值和偏离程度的概念,得到影响投标报价的主要因素,由历史数据分析得到所有厂家报价的算术平均值的置信区间,以此为基础建立了基于合理低价中标的投标企业非合作博弈论优化模型.使用该模型进行投标,各公司的中标率得到了明显的增长,稳定在10%以上,取得了理想的结果.结果表明: 报价模型提高了企业中标率,同时模型更接近实际报价情况.

合理低价中标; 绩效值; 偏离程度; 置信区间

Abstract: With the development of competition in power equipment industry,the scientific and practical requirements of bidding decision will be more improved.To construct and implement effective bidding strategies,in order to improve the bidding enterprises successful rate,by introducing performance value and the degree of deviation from the concept and main factors of affecting the bidding,by historical data analysis all manufacturers offer the arithmetic average value of the confidence interval is obtained.The basis is established based on reasonable low price winning the bid enterprise non cooperative game theory to optimize model.Using this model to tender,the company's bid rate has been significantly increased,stable at more than 10%,the achieved satisfactory results.The results show that the quotation model improves the winning rate,and the model is closer to the actual price.

Key words: rational low winning price,performance values,deviation degree,confidence interval

0 引言

投标报价是一门学问,普遍存在于当代商贸和工程项目中[1].在报价时,要注意采用合理的策略和方式,过高的报价容易导致竞争力缺失,过低的报价则会导致利益的损害.在兼顾中标率和所获利润的同时,如何进行合理的报价[2],引起了国内外专家学者的普遍兴趣.

1956年,Lawrence Friedman[3]采用运筹学的分析方法,针对投标中第一价格未知的情况,提出了最优竞价模型.之后,Gates[4]对此模型进行了优化和改进,而Cart则从机会成本的角度考虑,对模型进行了重新构建.最优规划法和供应函数均衡法也相继被引入到了投标报价问题中; 与此同时,博弈论的方法在一直被研究[5～10],特别是在信息不完备和存在合作或竞争关系时的报价策略方面取得了可喜的研究进展[11～16].冯卫兵[17]就非合作和比例动态下浮时的相邻物品投标价格问题,以提高中标率为约束条件,提出了非合作模式的动态下浮比例的连续批次投标报价问题.何星[18]则就无标底最低价中标法和复合标底招标法建立了博弈论报价模型.

然而,目前在投标报价方面还存在一定问题: 均采用实际报价与基准价差值最小作为最优报价,已有方法预测精度不高,报价效果不稳健.大多数现有的模型都以所有投标者均采用同一种稳定模式为前提,结合概率论和博弈论的方法进行构建,忽略了实际中变化莫测的市场环境和自身因素.

本文在区间平均下浮双边曲线算法的基础上,引入了绩效值和偏离程度的概念,从高于基准价和低于基准价两个不同层面进行了分析.并且通过置信区间的方法,分析得到了所有厂家报价的算术平均值的置信区间.在此基础上,提出了基于合理低价中标的投标企业非合作博弈论中标模型.实验表明,该模型对于公司的中标率有着显著的提升,并且具有一定的稳健性.

1 相关算法及概念

1.1 区间平均下浮双边曲线算法

企业能否中标,涉及技术、价格、商务等多种因素,一般来说,价格得分的高低是能否中标的关键.不考虑技术和商务等因素对中标的影响,先介绍区间平均下浮双边曲线算法的一些概念.

设某批次某个包有K个公司参加报价,投标价格分别为Pk,k=1,2,…,K,则其算数平均值为

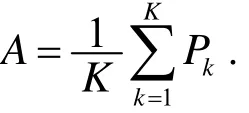
设参加该批某个包报价的K个公司中有L个公司的报价落入范围[0.8A,1.15A],其报价为,这L个公司的的报价的平均值为,则基准价为B=A1(1-a).其中a为下浮系数(或称下浮比例),一般会提前给出.从而得到K个公司的投标报价得分的计算公式

其中m,n为减分速率指数,一般也会提前给出.

1.2 绩效值

从以往招标的数据可知,虽然同一批次不同包的投标价格与最高限价的比值相差悬殊,但相对于成本来说却是一个固定值,这种显著差异是由于交货地点、中标单位与需求单位的地理位置造成的.这样我们需将第i批第j个包的招标报价Pi,j分为几个部分: 商品成本价Ci,j(可以认为是一个固定常数),利润Ui,j(可以认为是一个符合正态分布的量),运输等其它成本Vi,j(可以认为是一个与运输距离有线性关系的量),即Pi,j=Ci,j+Ui,j+Vi,j.

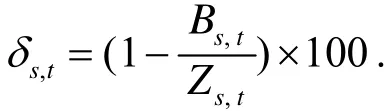
其中Bs,t、Zs,t分别为第批第t个包的标准价与最高限价.

这样一来,可以把每一批次中的最大绩效值对应的报价看作是运输等其它成本Vs,t的招标报价.

1.3 偏离程度

由于参加投标的厂家每年基本固定,各投标公司对每次报价都有自己的最优报价预测,其投标报价与基准价之间存在一定关系.通过分析其他公司的投标报价与基准价,发现二者之间存在一定的关联性:每家公司的报价与价格得分第一的报价之间的偏离有一定的规律,代表了其他投标公司报价及对最优报价的预测能力.

定义第k家投标厂家在第i批第j个包中的投标报价的偏离程度为

设第k家投标厂家在第i批招标中共参与了J个包的招标.当J≤3时,该企业在本批次招标的偏离程度不予计算; 当J≥4时,为了减少异常数据对整个均值的影响,采用如下的办法计算偏离程度的均值:

Step 1 计算该厂家在本批次参与的所有招标的偏离程度的算术平均值

Step 2 计算偏离程度的均值.设定阈值λ1,λ2(0≤λ1≤1,0≤λ2≤1),这里λ1=λ2=0.5,确定偏离程度区间的初范围.再求包含于上述区间的J′个偏离程度的算术平均值,即第k家投标厂家在第i批招标中的均值

国家电网2013～2014年共五批招标报价的偏离程度情况见表1和表2.

表1 偏离程度的均值

表1 偏离程度的均值

2013年第5批 2013年第6批2014年第1批2014年第2批 2014年第3批ABB 4.0760 1.5250 0.1137 3.0982 1.2789上虞 −0.7725 −1.9553 −2.8906 −1.0793 −4.0387中原 −1.1386 −2.7111 −1.2299 / /合容 −0.7456 −1.8262 −1.4991 −1.1176 −6.4287库柏 −6.4126 −7.43333 −2.1315 −2.1151 −5.1127思源 −3.5417 −1.5952 −2.7101 −1.7822 −2.9856恒顺 −6.3594 −1.8167 −0.9176 −5.2002 −3.8930新东北 −0.8768 −1.0624 −0.8927 −0.6756 −4.3613日新 −0.0676 3.7350 1.5638 0.8064 0.4231桂容 −0.8179 −2.4620 / −2.3006 −3.9406桂林 −0.6879 −3.9771 −3.1648 / /永锦 −0.8037 −4.7957 −3.7317 −1.2388 −2.3110泰开 −0.7037 −0.6182 −0.9574 −1.0461 −2.1162苏容 −1.0271 −1.7575 −2.0830 / /苏州 −3.2498 −2.4931 / −2.7601 −2.3082西电 −0.8853 −1.4432 −1.1730 −3.3628 −14.1830豫电 −3.2086 −2.6100 / −0.7063 −3.4750赛晶 −0.6235 −1.2595 −1.9119 −0.5837 −1.1970迪生 −4.718 / −8.6190 −12.1210 −4.5515顺容 −2.183 −0.6295 −4.2168 −0.8586 −9.3069

表2 偏离程度的方差

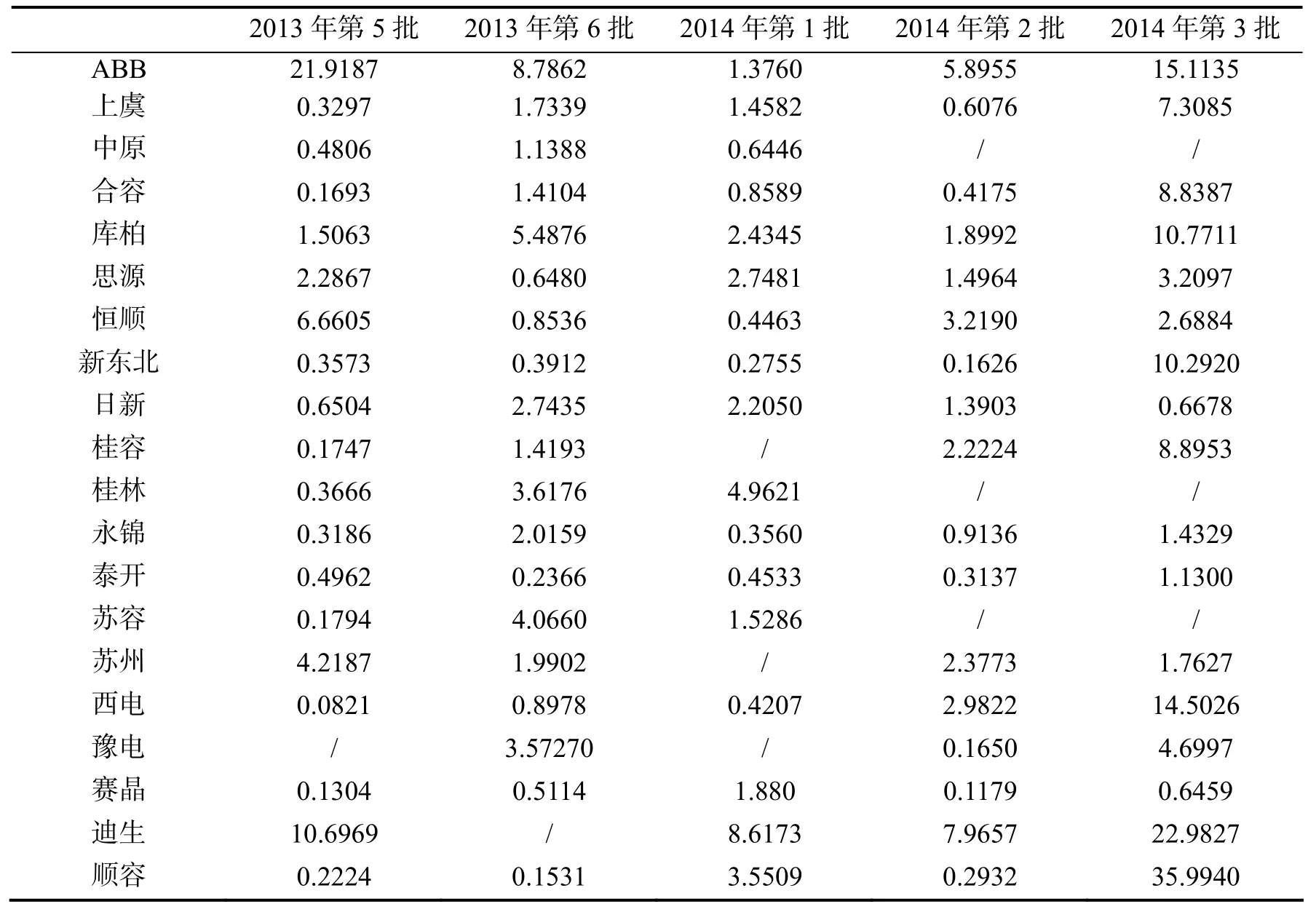
表2 偏离程度的方差

2013年第5批 2013年第6批2014年第1批2014年第2批 2014年第3批ABB 21.9187 8.7862 1.3760 5.8955 15.1135上虞 0.3297 1.7339 1.4582 0.6076 7.3085中原 0.4806 1.1388 0.6446 / /合容 0.1693 1.4104 0.8589 0.4175 8.8387库柏 1.5063 5.4876 2.4345 1.8992 10.7711思源 2.2867 0.6480 2.7481 1.4964 3.2097恒顺 6.6605 0.8536 0.4463 3.2190 2.6884新东北 0.3573 0.3912 0.2755 0.1626 10.2920日新 0.6504 2.7435 2.2050 1.3903 0.6678桂容 0.1747 1.4193 / 2.2224 8.8953桂林 0.3666 3.6176 4.9621 / /永锦 0.3186 2.0159 0.3560 0.9136 1.4329泰开 0.4962 0.2366 0.4533 0.3137 1.1300苏容 0.1794 4.0660 1.5286 / /苏州 4.2187 1.9902 / 2.3773 1.7627西电 0.0821 0.8978 0.4207 2.9822 14.5026豫电 / 3.57270 / 0.1650 4.6997赛晶 0.1304 0.5114 1.880 0.1179 0.6459迪生 10.6969 / 8.6173 7.9657 22.9827顺容 0.2224 0.1531 3.5509 0.2932 35.9940

2 基于合理低价中标的投标企业非合作博弈论优化模型

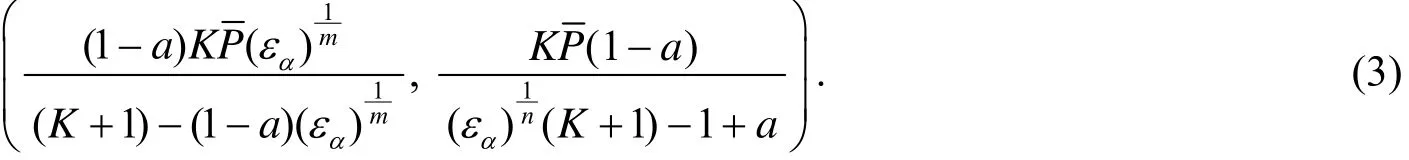
由上式可得出,关于报价Pα的求解转化为对在有效范围内的报价公司数K及其投标价的算术平均值的求解.

其他公司投标时都会面临同样的问题,都会对最优报价进行预测,这样所有的参与公司都会预测一个最优报价均衡,这个均衡对所有的投标公司是均等的,也是稳定的均衡,这就是采用“区间平均下浮双边曲线算法”确定基准价可以用博弈理论进行分析预测的基础.

由前面的讨论可知,招标价是由商品成本价Ci,j、利润Ui,j、运输等其它成本Vi,j组成,因此每个包的基准价B可以由每家企业的利润最低预期反推而得到基准价B的范围为

基于合理低价中标的投标企业非合作博弈论优化模型的具体建立过程如下:

(1)预测其它报价公司投标价的偏离程度的置信区间和频数

利用第k家公司的第i批第j个包投标报价的偏离程度,确定该公司的偏离程度范围及其相应频数Gk,具体方法如下:

Step 1 设第k家公司的第i批投标报价中的均值为,方差为,引入该公司的偏离程度的置信区间,其中η(k)(＞0)是调节系数,并设落入上述区间范围内的频数为.其中表示该公司在第i批投标中投的包数,表示该公司在第i批投标中偏离程度在公式(3)范围内的包数.

Step 2 求第k家公司在已知的所有批次(设共有w个批次)投标报价的偏离程度的置信区间及其频数的算术平均,得到第k家公司投标的偏离程度的置信区间和频数Gk.其中

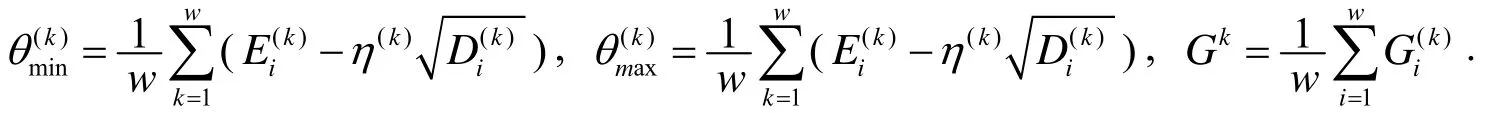
(2)预测其它K家公司投标价的算术平均值A的置信区间

先确定第k家公司投标价格P(k)的范围及其可信度,然后再求得其它厂家的投标价的算术平均值A的置信区间.

Step 1 确定第k家公司投标价格P(k)的范围.为使得该公司提高中标率,需选取,因此

Step 2 利用第k家公司投标价格P(k)的范围,可以得到其它K家厂家的投标价的算术平均值A的置信区间为

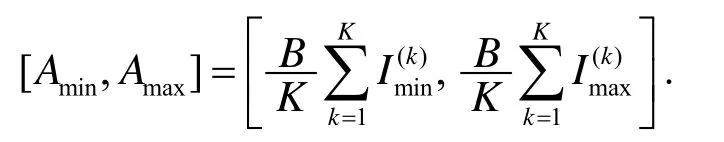
由于各个厂家投标的独立性,可得落入该区间的相应概率为

(3)预测指定范围内的公司投标价的算术平均值的置信区间及相应的概率

利用第k家公司投标价格P(k)的取值范围与区间[0.8Amin,1.15Amax]的交集,由式(2)知可设为(注意部分为空集),其对应的区间长度记为ρ(k)(空集的长度为0),这样就可以得到算术平均值的置信区间为

落入该区间的概率G仍为(4).

(4)得分率阈值的选取

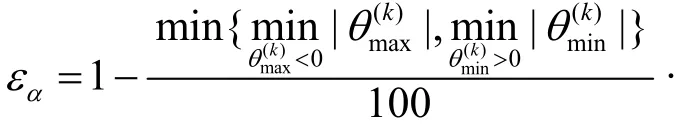
其报价Pα的范围见公式(3).

(5)本公司投标报价优化模型

利用前面的四步,得到了如下优化模型

3 实验及结果分析

在基于假设: 国家电网设置的最高限价是合理的,所有的投标厂家都是理性的,各个厂家在技术、商务等方面实力基本相当的前提下,运用上述的基于合理低价中标的投标企业非合作博弈论模型,对国家电网2013年至2015年每年举行的6批电容器类货物的招标中每个公司的中标概率做了相关的实验.

通过实验发现,使用上述建立的模型,对各个公司的中标率都有着显著而又稳定的提高.以合容公司在2013年第5批所有包的中标数为例,由原先的2次,增加到了10次,中标率由3.39%提高到18.64%,取得了理想的结果.可见使用该模型对报价进行预测,可以显著提高企业中标率,同时模型更接近实际报价情况.表3中列出了2013年第五批所有公司的中标情况.

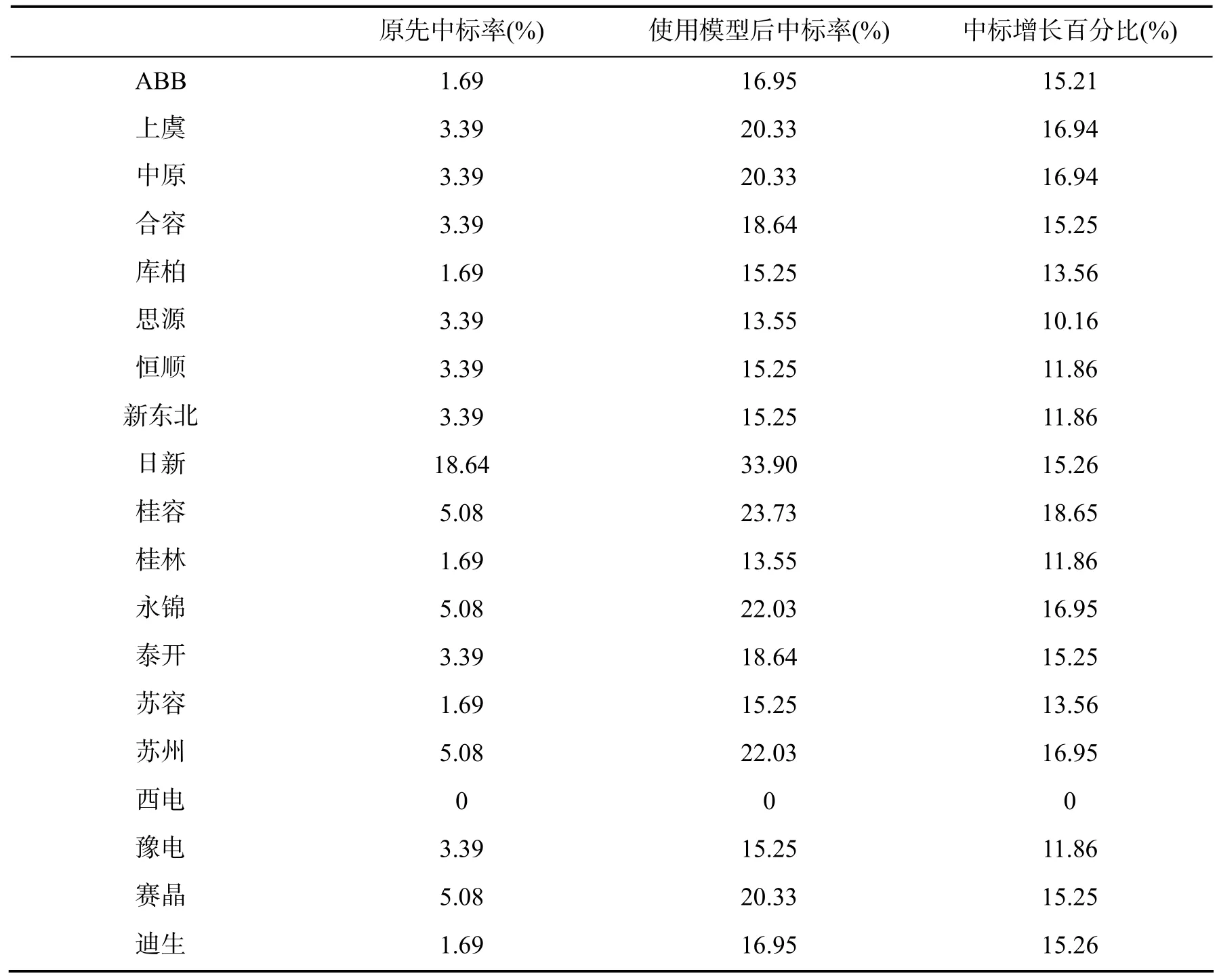
表3 2013年第五批各公司中标率

由表3可以看出,使用基于合理低价中标的投标企业非合作博弈论模型后,各公司的中标率都有了显著的增长,而且增长幅度都稳定在10%以上,最低为10.16%,最高为18.65%,取得了理想的效果.

4 结束语

每次招标投标进程都是一场博弈,一场涉及到投标人和招标人、投标人之间的利益分配,并且相互之间互有影响.各投标方不能完全了解对方的信息和决策,只能靠预测制定自己的报价,这里的报价相当于决策,且在投标时以密封形式给出,因而可采用基于不确定信息的静态博弈法.合理低价中标可使各投标人在相对公平的条件下进行投标,遵循市场经济的原则,企业自主报价,一定程度上可阻止投标人和中标者的不诚信交易.

结合企业在参加投标时应该考虑的定性和定量因素,运用博弈论,并构造了适合参加国家电网公司当前的这种招标、评标方式的基于合理低价中标的投标企业非合作博弈论模型,这对于企业在制定科学的投标报价决策和策略方面起到了积极的指导作用.

同时对国家电网的招标提出如下建议: 建立投标公司的诚信机制,减少某些厂家不切实际的报价; 对于最高限价按区域划分成几类,从而减少同一批次的不同包的投标价格偏离太大.

[1]Lin Y,Yongxian W,Tao Z.Bidding decision model for complex bids[J].Journal of Tsinghua University: Soience and Technology,2006,46(12): 2053～2 056

[2]Peilin D,Jianxin Y.Strategic analysis of competition in inviting and taking bidding[J].Mathematic in Practice and Theory,2011,41(12): 94～96

[3]Gate M.Bidding strategies and probabilities[J].Journal of the Construction Division,1967,93 (1): 74～107

[4]Campgbell M C.Perceptions of price unfairness antecedents and consequences[J].J Marketing Researc,1999,36(5):187～199

[5]Dikmen I,Birgonul M T.A case-based decision support tool for bid markup estimation of international construction projects[J].Automation in Construction,2007(10): 30～44

[6]郭清娥,王雪青.基于交叉评价和模糊理论的工程项口投标决策方法研究田运筹与管理[J].运筹与管理,2012,21(6): 100～104

[7]武智勇,康重庆,夏 清,等.基于博弈论的发电商报价策略[J].电力系统自动化,2002,26(9): 7～11

[8]黄宏飞,欧国立.博弈论在投标报价决策中的应用[J].北京交通大学学报,2000,24(3): 41～43

[9]Hao L P,Zheng Y T,Tan Q M.Game theory model quotation of price in biding for construction projects[J].Journal of Harbin University of Civil Engineering & Architecture,2002,35(2):109～112

[10]Washington C.The Identity Theory of Quotation[J].Journal of Philosophy,1992,89(11): 153～172

[11]Xu S D,Cai X L,Liu W.The determination of best bid price quotation based on game theory[J].Applied Mechanics & Materials,2012,155～156(5): 450～454

[12]Fei M Q.Research on Tax-related Authentication under the Dynamic Game Theory of Incomplete Information[J].Accounting & Economics Research,2012

[13]Ying L I.Game Analysis of Safety Supervision in Local Coal Mine Based on the Game Theory of Incomplete Information[J].Industrial Safety &Environmental Protection,2007

[14]Dimitrov N B.Coping with dynamic membership,selfishness,and incomplete information:applications of probabilistic analysis and game theory[C].University of Texas at Austin,2008

[15]李 为,苏林萍,王 鑫.基于不完全信息博弈论的发电厂竞价策略[J].华北电力大学学报(自然科学版),2006,33(4): 36～38

[16]王维国,刘德海.建筑工程项目招标低价中标现象的不完全信息博弈理论分析[J].中国管理科学,2008(s1): 444～449

[17]冯卫兵.非合作模式下动态下浮比例连续批次投标报价模型[J].西安科技大学学报,2015(4): 505～510

[18]何 星.工程项目投标决策和报价模型研究[D].西安: 西安建筑科技大学硕士学位论文,2008

A Non-cooperative Game Theory Optimization Model of Bidding Enterprises based on Reasonable Low price

ZHANG Hairui1,LI Songhua2,ZHOU Linlin1,FENG Caiying1
(1.College of Information and Communication Engineering,Hunan Institute of Science and Technology,Yueyang 414006,China;2.College of Mathematics,Hunan Institute of Science and Technology,Yueyang 414006,China)

F224

A

1672-5298(2017)03-0013-07

2017-01-24

张海瑞(1991− ),男,山西忻州人,湖南理工学院信息与通信工程学院硕士研究生.主要研究方向: 计算智能与模式识别