基于波片的邦加球上任意偏振态的转换方法

万 婷,罗朝明,陈 敏,刘 靖

(湖南理工学院 信息与通信工程学院,湖南 岳阳 414006)

基于波片的邦加球上任意偏振态的转换方法

万 婷,罗朝明,陈 敏,刘 靖

(湖南理工学院 信息与通信工程学院,湖南 岳阳 414006)

为了实现邦加球上任意偏振态之间的转换,在研究波片对偏振态影响规律的基础上,提出了一种基于波片的邦加球上任意偏振态的转换方法.通过琼斯矩阵理论研究得到了波片在邦加球上偏振态的转换规律,波片能实现邦加球同一纬度值不同半球任意两点对应偏振态的转换,从而实现邦加球上经度的调节;波片不仅能够实现邦加球上任意一点到赤道对应偏振态,还能实现赤道到0°经线上任意一点对应偏振态的转换,因而可实现纬度的调节.基于上述规律,提出了利用两个波片和两个波片实现邦加球上任意两点偏振态之间的转换方法,并给出了具体的转换思路,同时以邦加球上偏振态的转换为例,仿真验证了这种方法的有效性.

偏振态; 转换方法; 琼斯矩阵理论; 波片; 邦加球

Abstract: In order to implement the conversion between arbitrary polarization states on the Poincaré sphere,a conversion approach based on waveplates is proposed in view of the influence of waveplates on polarization state.The conversion laws of polarization states on the Poincaré sphere can be obtained with Jones matrix theory.It is shown that the half-wave plate can realize the conversion of arbitrary longitude on a certain fixed latitude of the two different hemispheres,thus the longitude of the Poincaré sphere can be adjusted.In addition,the quarter-wave plate can not only convert from any arbitrary point on the sphere to the equator,but convert from any point on the equator to the 0° longitude,therefore the latitude can also be adjusted.On the basis of the above laws,the conversion between arbitrary polarization states can be realized by using two half-wave plates and two quarter-wave plates.The detailed conversion procedure is given,and the conversion from the polarization stateconfirms the validity of the conversion approach.

Key words: polarization state,conversion approach,Jones matrix theory,waveplate,Poincaré sphere

0 引言

偏振作为光的一个重要性质,广泛应用于通信技术、激光技术、光电子技术、图像技术等领域[1～4],因此对光的偏振态描述及其转换进行研究具有非常重要的意义.常用来描述偏振态的方法有: 椭圆方程法、琼斯矩阵法、斯托克斯矢量表示法和邦加球表示法[1,2,5].其中邦加球表示法是一种最为直观、形象的表示方法,它能将每一种可能的偏振态映射到一个单位球的表面来描述,为解决一些复杂的偏振问题提供了一种简便的理论分析思路.邦加球理论由Poincaré于1892年提出,随后其相关理论得到不断发展并被广泛应用于不同领域.早期人们利用邦加球理论来分析偏振光通过偏振器件、双折射材料以及光学系统后的出射光偏振态的变化情况[6,7],并将得到的结果应用于液晶显示参数优化中,进而提升液晶显示器的可视化效果[8～10].对于光纤中存在的偏振模色散问题,使用邦加球不仅可以简单直观地描述光纤中偏振态的变化过程,而且还能根据光纤中偏振态的演变情况来补偿偏振模色散[11～14]; 借助邦加球还可以描述偏振态经过系统的传输演变情况,达到设计和优化相关光网络器件的目的[15～17].随着研究的深入,邦加球相关理论的应用逐步从光学领域扩展到生物医学、图像技术等领域.Acdonald C等利用光学追踪标记后向散射光经过生物组织的偏振态在邦加球上的变化情况,并将该方法用于癌组织细胞以及混浊组织样本的检测[18～19]; 在图像技术领域,Anna G和Vannier N等通过调节邦加球上偏振态分布增强了图像的对比度[20～22].与此同时邦加球理论也在不断加深,Holleczek 等人借鉴邦加球理论提出了高阶邦加球来描述矢量光束[23～26].

尽管人们对邦加球理论及其相关应用进行了较广泛的研究,但大多集中在利用邦加球来描述光束通过波片或某一系统后的偏振态变化情况[6～19,25],而对如何实现邦加球上任意偏振态之间的转换方面的研究还不够深入,因此找到一种实现邦加球上任意偏振态之间的转换方法具有较为重要的意义.本文通过琼斯矩阵理论推导了波片在邦加球上任意偏振态之间的转换规律,并以此为基础提出一种利用波片来实现邦加球上任意偏振态之间的转换方法,同时通过具体实例仿真验证了这种方法的有效性.

1 偏振态在邦加球上的表示

先简要介绍一下不同偏振态在邦加球上的表示方法,以便于探索偏振态在邦加球上的转换规律.邦加球是一个用来描述均匀偏振光偏振态的单位球,球上任意一点偏振态ζ可用一组归一化的斯托克斯参数组成的坐标(S1,S2,S3)来表示,也可用球坐标(θ,φ)来表示,具体如图1所示.这里的斯托克斯参数定义为[26,27]

其中L和R分别表示左旋圆偏振态和右旋圆偏振态,对应邦加球上的北极和南极,其数学表达式分别为[27]

其中θ对应纬度相关参量,对应经度相关参量.

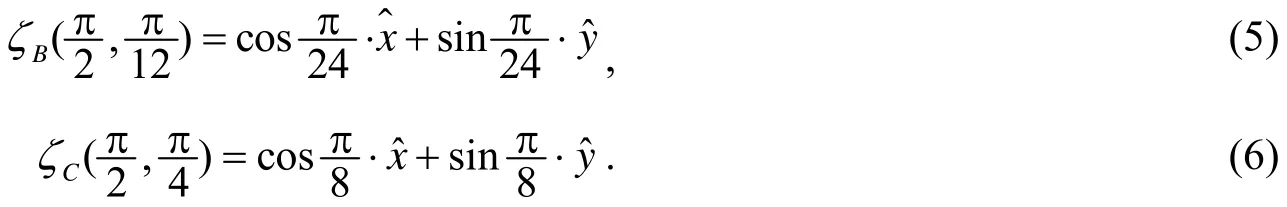
图1 邦加球及其偏振态表示

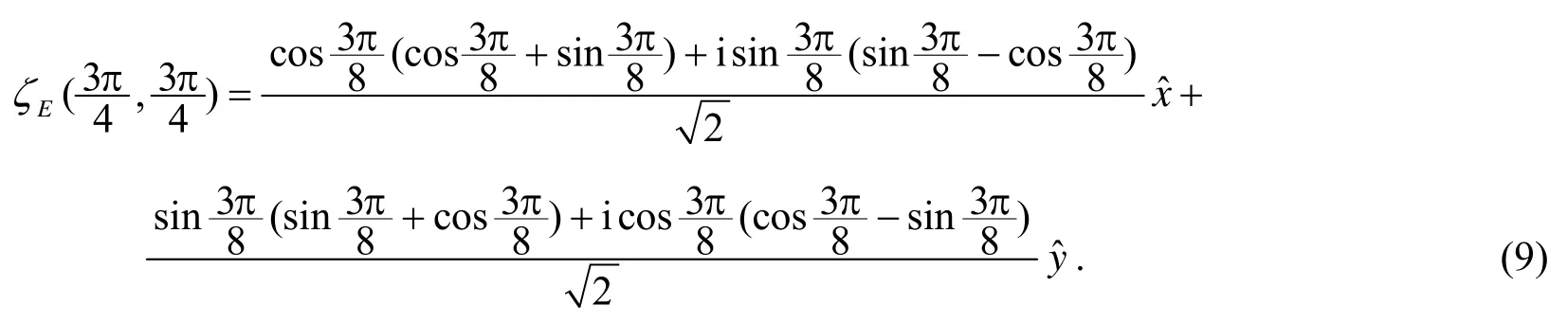
2 波片在邦加球上偏振态的转换规律

为了研究基于波片的邦加球上任意偏振态之间的转换,有必要分析波片在邦加球上偏振态转换中的作用规律.将邦加球上任意一点偏振态ζ(θ,φ)对应的表达式(4)写成琼斯矢量形式,可得入射光的琼斯矢量为

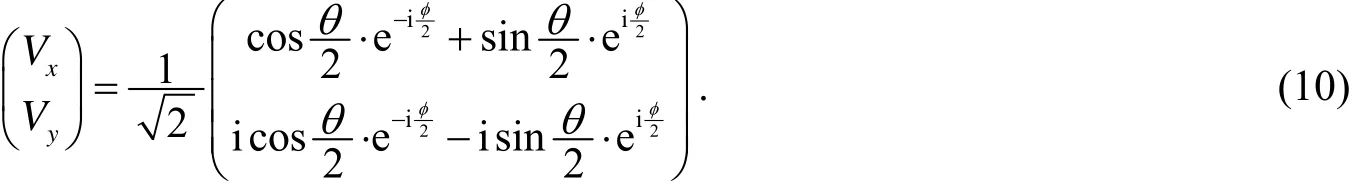
根据式(10)和(11),可以得到出射光对应的琼斯矢量为[2]

2.1 偏振态经过波片在邦加球上的转换规律

图2 邦加球上偏振态经过半波片转换规律示意图

比较式(10)和(13)可知,将入射光偏振态琼斯矢量中纬度相关参量θ变为、经度相关参量变为-ψ+4φ就可以得到出射光偏振态的琼斯矢量,因此该转换过程将入射光偏振态ζ(θ,φ)转化为了出射光偏振态ζ(π-θ,-φ+4ψ).进一步可得,波片可实现邦加球上同一纬度值不同半球任意两点偏振态之间的转换,这一转换规律可用图2来形象描述.如图1中位于不同半球具有相同纬度值的到的转换,只需使其方位角满足关系式,即设置波片方位角为.同理,波片还能够实现赤道上任意两点对应线偏振态以及南北两极对应圆偏振态之间的转换.

2.2 偏振态经过波片在邦加球上的转换规律

假定入射光偏振态仍为邦加球上任意一点对应的偏振态ζ(θ,φ),同时设置波片的方位角为,由式(12)很容易得到出射光琼斯矢量为

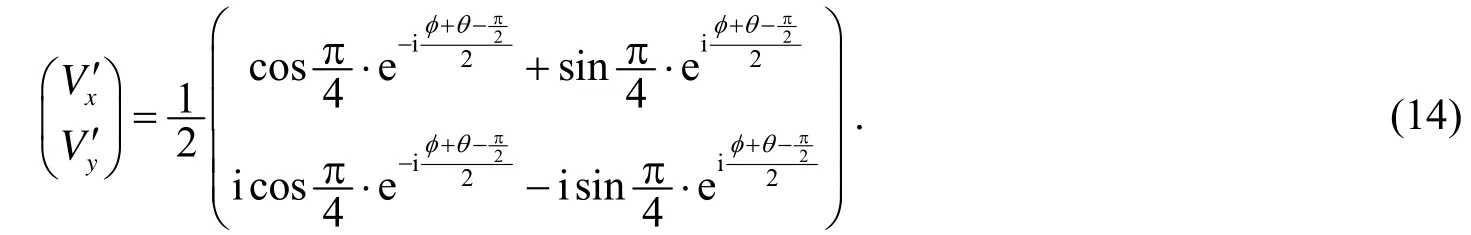
图3 邦加球上椭圆(或圆)偏振态转换为线偏振态的转换规律示意图

(2)线偏振态经过方位角ψ=0的波片的转换规律

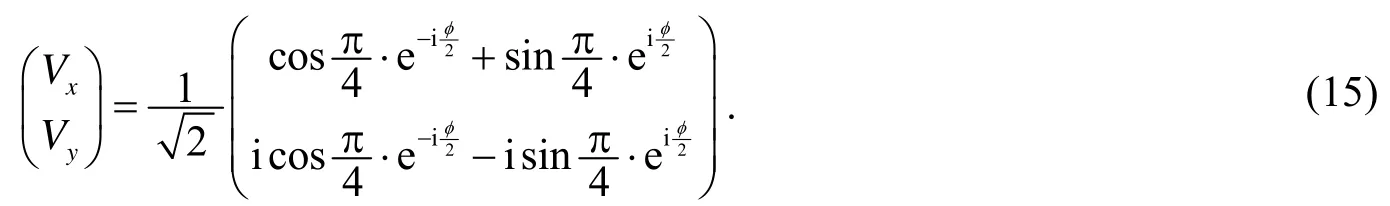
通过式(12)与式(15)可以得到出射光偏振态的琼斯矢量为

将式(15)与式(16)进行比较,类似于前面分析可以得出: 经过方位角ψ=0的波片后,赤道上入射线偏振态转换成了出射偏振态,该转换规律如图4所示.纬度相关参量由变为了,经度相关参量由变为了0,由此可知使用方位角ψ=0的波片可以实现邦加球上赤道对应线偏

振态到0°经线上对应的偏振态的转换,且借助于经度相关参量可实现对纬度的调节.如图1中赤道上到0°经线上的转换,只需设置波片的方位角ψ=0.

图4 邦加球上线偏振态转换为椭圆(或圆)偏振态的转换规律示意图

3 邦加球上任意两点偏振态的转换

图5 邦加球上任意两点偏振态的转换示意图

现在进一步确定这四个波片的方位角的设置以及经过波片后对应的偏振态.设第一个、第二个波片的方位角分别为ψH1和ψH2,第一个、第二个波片的方位角分别为ψQ1和ψQ2.第一个波片的作用是实现球上的H点到赤道上I点的转换,根据图3所示的转换规律只需将该波片的方位角设置为即可,得出I点对应的偏振态为;根据图2所示的规律,不同半球同一纬度值的0°经线上的M点和N点的转换,可借助方位角为的第二个波片实现,且可求出M点对应的偏振态为ζM(π-θ2,0); 第二个波片的作用是实现赤道上J点到0°经线上M点的转换,根据图4所示的转换规律将该波片的方位角设置为ψQ2=0,同时也可求得赤道上J点对应的偏振态为; 关于赤道I点到J点的转换,同样可借助波片实现,只需设置第一个波片的方位角为即可.

最后以图1中邦加球上A点到E点的转换为例来论证这种方法的有效性.由于A点与E点所对应的偏振态分别为,可得出.转换步骤为: 第一步,将具有A点偏振态的光束经过波片转换到赤道上,该点对应的偏振态为,即对应图1中的B点; 第二步,利用波片对赤道上的经度进行合适的调节,只需取波片的方位角即可实现该转换,转换得到的点对应的偏振态为,即对应为图1中的C点; 第三步,使用方位角ψQ2=0的波片转换到与E点纬度值相同但位于不同半球的0°经线上的点,对应的偏振态为,即对应图1中的D点; 最后,利用方位角波片实现到E点所对应的偏振态的转换.

很明显,该例子有效地验证了这种基于波片的邦加球上转换方法的可行性.

4 总结

本文提出了一种基于波片的邦加球上任意两点偏振态之间的转换方法.首先,分析总结了波片和波片在邦加球上的作用规律,波片能够使球上任意一点偏振态ζ(θ,φ)转化为另一半球相同纬度值上对应的偏振态ζ(π-θ,-ψ+4φ),从而实现纬度值相同但位于不同半球两点的任意变换;波片不仅能使球上任意一点偏振态ζ(θ,φ)转换为赤道上的线偏振态,而且还能使赤道上对应的线偏振态转换为0°经线上对应偏振态,从而能够实现纬度的调节.其次,基于波片和波片在邦加球上的作用规律,提出使用两个波片和两个波片实现邦加球上任意两点偏振态之间的转换方法.具体转换步骤为: 首先设置第一个波片的方位角为,将入射偏振态转换到赤道上对应的线偏振态,然后设置第一个波片的方位角为调节到赤道上合适的线偏振态,这个合适的线偏振态满足使用第二个方位角为0的波片可以转换到与终点偏振态纬度值相同的不同半球的0°经线上的偏振态,最后设置第二个波片方位角为来实现到出射偏振态的转换,并通过具体实例仿真验证了这种方法的有效性.本文的研究结果将有助于分析与设计偏振转换器件和系统,从而扩展邦加球在偏振分析方面的应用范围.

[1]Goldstein D H.Polarized light[M].New York: Marcel Dekker,2003: 454～484

[2]Amnon Yariv,Pochi Yeh.Photonics:Optical Electronics in Modern Communications[M].New York: Oxford University Press,2007: 28～55

[3]李 浩,朱京平,张 宁,等.半波片角度失配对通道调制型偏振成像效果的影响及补偿[J].物理学报,2016,65(13): 134202

[4]李英超,王 超,安 岩,等.水下隐身动目标激光与偏振红外探测技术研究[J].激光与红外,2016,(2): 209～213

[5]BOM M,WOLF E.Principles of optics[M].New York: Pergamon Press,1980: 25～31

[6]Azzam R M A,Bashara N M.The effect of an optical systems in the complex-plane and the Poincare-sphere representation[J].Optics Communications,1972,5(5): 319～322

[7]Martinelli M.A universal compensator for polarization changes induced by birefringence on a retracing beam[J].Optics Communications,1989,72(6):341～344

[8]Bigelow J E,Kashnow R A.Poincaré sphere analysis of liquid crystal optics[J].Applied Optics,1977,16(8): 2090～2096

[9]Zhuang Z,Kim Y J,Patel J S.Parameter optimization for a reflective bistable twisted nematic display by use of the Poincaré sphere method[J].Optics Letters,1999,24(16): 1166～1168

[10]Kim T,Lee J H,Yoon T H,et al.Reflective dual-mode liquid crystal display possessing low power consumption and high contrast ratio under ambient light[J].Optics Express,2012,20(14): 15522～15529

[11]张德生,孙 磊,董孝义.邦加球在分析光纤偏振态传输中的应用[J].光电子·激光,2003,14(10): 1099～1102

[12]刘开贤,张 霞,赵京玺,等.用庞加莱球法测量二阶偏振模色散[J].光学学报,2004,24(5): 583～586

[13]Williams P A,Dennis T.Direct Measurement of Vector Polarization-Mode Dispersion From Repeated Random Data by Use of Linear Optical Sampling[J].IEEE Photonics Technology Letters,2010,22(5): 326～328

[14]Krummrich P M,Ronnenberg D,Schairer W,et al.Demanding response time requirements on coherent receivers due to fast polarization rotations caused by lightning events[J].Optics Express,2016,24(11): 12442～12457

[15]Zhao S,Wu C,Cheng M,et al.Poincare Sphere Method for Optimizing the Wavelength Converter Based on Nonlinear Polarization Rotation in Semiconductor Optical Amplifiers[J].IEEE Journal of Quantum Electronics,2009,45(8): 1006～1013

[16]Connelly M J.Modeling of nonlinear polarization rotation in tensile-strained semiconductor optical amplifiers using Mueller matrices and carrier density induced refractive index change calculations[J].Optics Communications,2013,308(1): 70～73

[17]Guasoni M,Bony P Y,Gilles M,et al.Fast and chaotic fiber-based nonlinear polarization scrambler[J].IEEE Journal of Selected Topics in Quantum Electronics,2016,22(2): 88～99

[18]Macdonald C,Meglinski I.Backscattering of circular polarized light from a disperse random medium influenced by optical clearing[J].Laser Physics Letters,2011,8(4): 324

[19]Kunnen B,Macdonald C,Doronin A,et al.Application of circularly polarized light for non-invasive diagnosis of cancerous tissues and turbid tissue-like scattering media[J].Journal of Biophotonics,2015,8(4): 317～323[20]Anna G,Sauer H,Goudail F,et al.Fully tunable active polarization imager for contrast enhancement and partial polarimetry[J].Applied Optics,2012,51(21): 5302～5309

[21]Vannier N,Goudail F,Plassart C,et al.Active polarimetric imager with near infrared laser illumination for adaptive contrast optimization[J].Applied Optics,2015,54(25): 7622～7631

[22]Vannier N,Goudail F,Plassart C,et al.Comparison of different active polarimetric imaging modes for target detection in outdoor environment[J].Applied Optics,2016,55(11): 2881～2891

[23]Holleczek A,Aiello A,Gabriel C,et al.Classical and quantum properties of cylindrically polarized states of light[J].Optics Express,2011,19(10):9714～9736

[24]Chen S,Zhou X,Liu Y,et al.Generation of arbitrary cylindrical vector beams on the higher order Poincaré sphere[J].Optics Letters,2014,39(18):5274～5276

[25]Naidoo D,Roux F S,Dudley A,et al.Controlled generation of higher-order Poincaré sphere beams from a laser[J].Nature Photonics,2016,10(5):327～332

[26]罗朝明,陈世祯,凌晓辉,等.高阶邦加球上柱矢量光束的变换[J].物理学报,2014,63(15): 154203

[27]Milione G,Sztul H I,Nolan D A,et al.Higher-order Poincaré sphere,Stokes parameters,and the angular momentum of light[J].Physical Review Letters,2011,107(5): 053601

[28]Milione G,Evans S,Nolan D A,et al.Higher order Pancharatnam-Berry phase and the angular momentum of light[J].Physical Review Letters,2012,108(19): 190401

Conversion Between Arbitrary Polarization States on Poincaré Sphere based on Waveplates

WAN Ting,LUO Zhaoming,CHEN Min,LIU Jing
(College of Information and Communication Engineering,Hunan Institute of Science and Technology,Yueyang 414006,China)

O436.3

A

1672-5298(2017)03-0020-07

2017-06-08

湖南省教育厅科学研究优秀青年项目(17B114); 湖南省自然科学基金(2017JJ3098); 湖南省科技计划项目(2016TP1021)

万 婷(1993− ),女,湖南湘潭人,湖南理工学院信息与通信工程学院硕士研究生.主要研究方向: 光通信与信息器件

罗朝明(1978− ),男,湖南永州人,博士,湖南理工学院信息与通信工程学院副教授.主要研究方向: 微结构光子学及其器件