直觉模糊软集新的相似度及其应用

王金英



直觉模糊软集新的相似度及其应用

王金英

（辽宁工业大学 理学院，辽宁 锦州 121001）

将模糊软集的包含度拓展到直觉模糊软集中，针对参数集合不同的情况，给出直觉模糊软集一种新的相似度。首先，借助于直觉模糊集包含度，给出了直觉模糊软集包含度的公理化定义和三种不同的计算公式；然后，在直觉模糊软集包含度的基础上，提出了直觉模糊软集相似度的公理化定义及相应的计算公式；最后将这种新的相似性度量方法应用到实例分析中，说明了该方法的有效性和可行性。

模糊蕴涵算子；集合基数；直觉模糊软集；包含度；相似度

俄罗斯学者Molodtsov[1]于1999年首次提出了软集理论，该理论被认为是处理不确定性问题的一种有效的数学工具，从此软集理论的研究得到了学术界的广泛关注。学者们将软集分别与模糊集、直觉模糊集和区间值模糊集等数学模型相结合，构造了模糊软集[2]、直觉模糊软集[3-4]和区间值模糊软集[5]等扩展模型。近几年，模糊软集的不确定性度量成为学者们研究的热点之一。Majumdar等[6]研究了模糊软集的相似性度量；Jiang等[7]提出了直觉模糊软集的距离，并构造了直觉模糊软集与区间值模糊软集的熵度量；王玲等[8]结合平面直角坐标系，提出了区间值模糊软集的新的相似度量，进而给出了区间值模糊软集的距离度量；彭新东等[9]给出了区间值模糊软集信息测度的公理化定义及相应的公式，并讨论了它们的转换关系。以上文献中距离和相似度的研究都是在具有相同参数集合的条件下进行的，然而不同的模糊软集、直觉模糊软集以及区间值模糊软集可能有不相同的参数集合。于是，针对参数集合不同的情况，Liu等[10]提出了模糊软集之间的新的相似度和距离测度；洪智勇[11]基于模糊蕴含算子提出新的模糊软集包含度和相似度度量方法；刘雅雅等[12]给出在参数集合不同的情况下软直觉模糊集之间相似性的度量方法，但最后的实例应用却仍然是在参数集合相同的情况下进行的。因此，针对现有直觉模糊软集的相似度大多是基于距离测度且参数集合相同的现状，本文将文献[11]中模糊软集的包含度和相似度公式推广到直觉模糊软集，从包含度的角度研究了参数集合不同的情况下直觉模糊软集之间的相似度问题，并将新的相似度应用到实际决策中。

1 预备知识

本节回顾直觉模糊集、直觉模糊包含度以及直觉模糊软集的一些相关知识。

定义1[13]称为上的直觉模糊集，其中，对，和分别为中元素属于的隶属度和非隶属度，且满足条件≤≤。

定义2[13]设，定义运算如下：

定义3[14]设，若映射满足条件：

基于模糊蕴涵算子和直觉模糊集合基数，文献[3]提出了以下两种直觉模糊包含度：

(1)基于蕴涵算子的包含度

定义4[14]若映射满足条件：

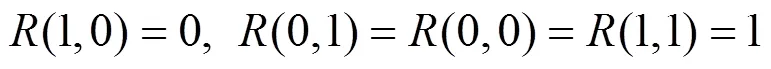
定理1[14]设，是一模糊蕴涵算子，若满足条件：

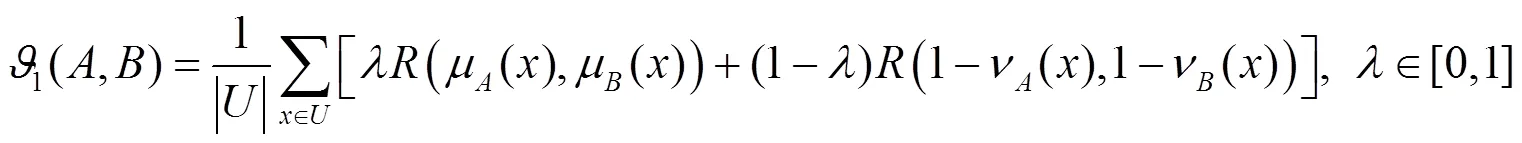
满足定理1条件的模糊蕴涵算子有：

(2)基于集合基数的包含度

定义5[14]设，定义的基数为

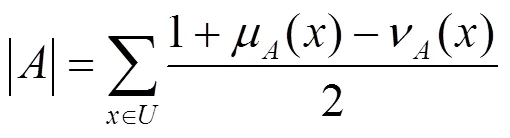
定理2[14]设，则均为直觉模糊集的包含度函数。

，

定义6[3]设是论域中对象的一个参数集，，且是一个映射，称序对为上的直觉模糊软集。

定义7[3]设，若且对，有，则称是的一个直觉模糊软子集，记作。

定义8[4]设，若对，有，则称是相对空直觉模糊软集，记作。

定义9[4]设，若对，有，则称是相对完全直觉模糊软集，记作。

对于上述两个定义，必须理解“相对”的含义，所谓的“相对”就是指任何一个相对空直觉模糊软集或者相对完全直觉模糊软集都是对于一个特定的属性集而言的[4]。

2 直觉模糊软集的包含度

将直觉模糊集的包含度推广到直觉模糊软集，下面给出直觉模糊软集包含度的公理化定义及其计算公式。

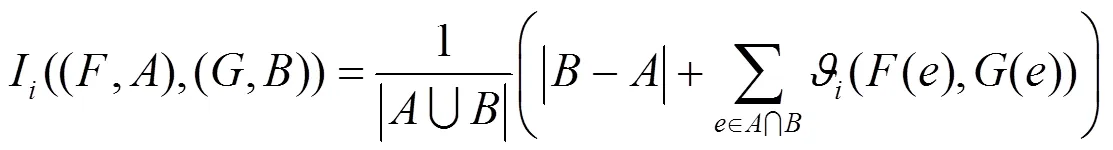
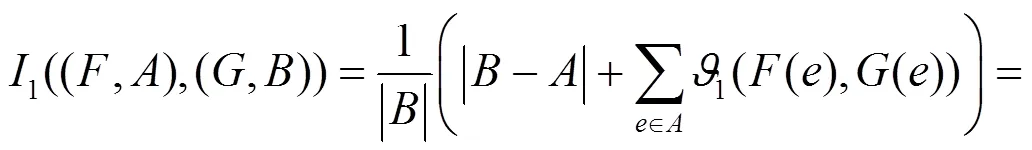
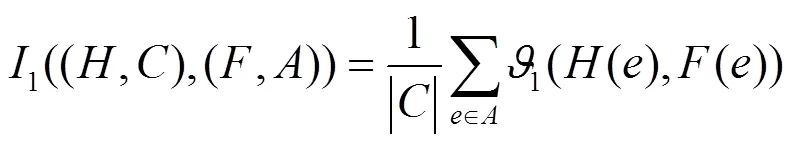
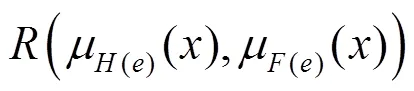
于是有：

≤

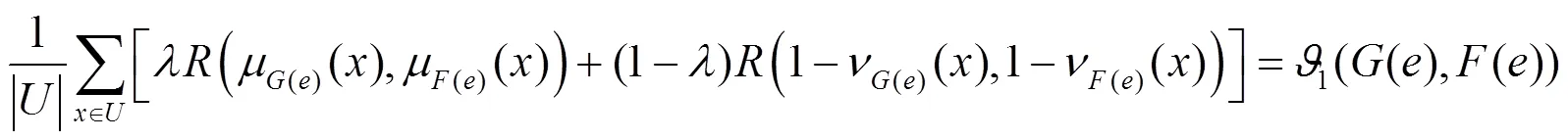
因此：

≤≤

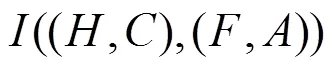
证明过程与定理3完全类似。

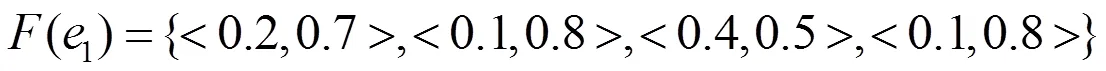
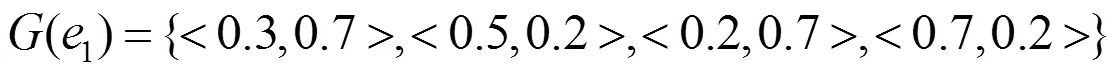
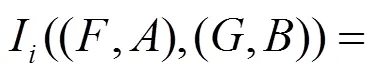
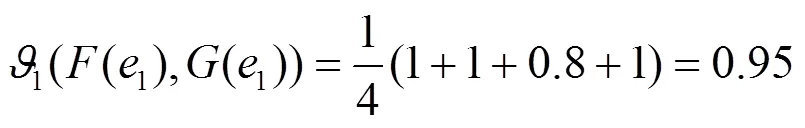
因此：

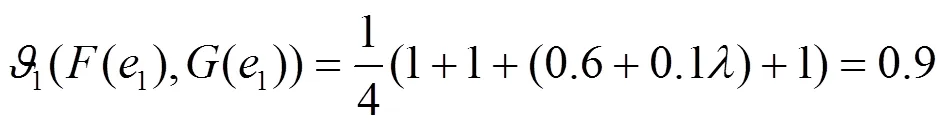
因此：

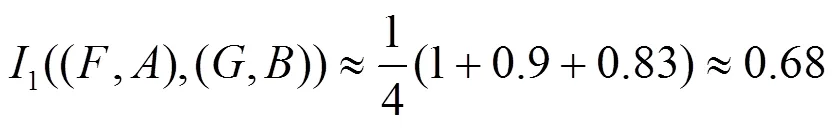
因此：

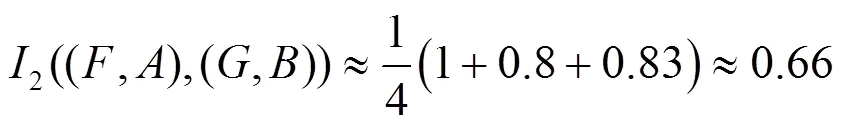
因此：

3 直觉模糊软集的相似度

基于直觉模糊软集的包含度，本节给出直觉模糊软集的相似度。

且：

≤，≤

由于：

因此：

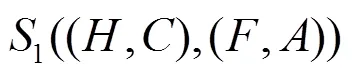
4 实例分析

在本节中，应用两个直觉模糊软集之间的相似度来评估某人购买衬衫的可能性。

假设现有两款衬衫A和B可供购买者选择，它们的特征可以通过两个直觉模糊软集和来描述，它们的表格形式如表1和表2所示。

表1 第一款衬衫的直觉模糊软集模型(F,A)

表2 第二款衬衫的直觉模糊软集模型(G,B)

根据购买者的要求，给出想要购买衬衫的标准直觉模糊软集模型，它的表格形式如表3所示。

表3 衬衫的标准直觉模糊软集模型(H,C)

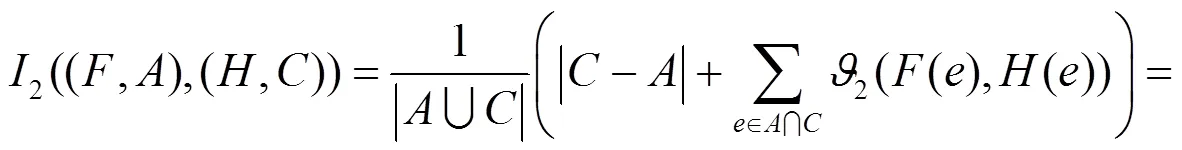
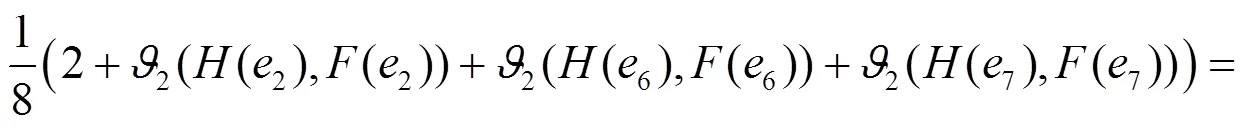
所以：

同理可得：

，

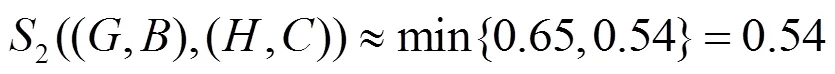
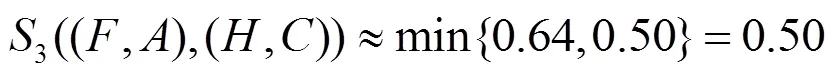
5 结束语

针对参数集合不同的情况，本文从包含度的角度，研究了直觉模糊软集的相似性度量问题。该方法借助于直觉模糊集包含度，给出了直觉模糊软集包含度的公理化定义和计算公式，进而构造了在参数集合不同的情况下直觉模糊软集的一种新的相似性度量，最后将这种基于包含度的直觉模糊软集的新的相似度应用到实例分析中，取得了良好的效果。

[1] Molodtsov D. Soft set theory—first results[J]. Comput Math Appl, 1999, 37(4): 19-31.

[2] Maji P K, Biswas R, Roy A R. Fuzzy soft sets[J]. Journal of Fuzzy Mathematics, 2001, 9(3): 589-602.

[3] Maji P K, Biswas R, Roy A R. Intuitionistic fuzzy soft sets[J]. Journal of Fuzzy Mathematics, 2001, 9(3): 677-692.

[4] 牛刚. 软直觉模糊集[J]. 计算机工程与应用, 2012, 48(18): 45-47.

[5]Yang X B, Lin T Y, Yang J Y, et al． Combination of interval-valued fuzzy set and soft set[J]. Computers and Mathematics with Applications, 2009, 58(3): 521-527.

[6] Majumdar P, Samanta S K. On similarity measures of fuzzy soft sets[J]. International Journal of Advance in Soft Computing and Its Application, 2011, 3(2): 1-8.

[7] Jiang Y C, Tang Y, Liu H, et al. Entropy on intuitionistic fuzzy soft sets and on interval-valued fuzzy soft sets[J]. Information Sciences, 2013, 240: 95-114.

[8]王玲, 秦克云, 刘雅雅.区间值模糊软集的相似度及距离和熵[J]. 济南大学学报:自然科学版, 2015, 29(5): 361-366.

[9]彭新东, 杨勇.区间值模糊软集的信息测度及其聚类算法[J]. 计算机应用, 2015, 35(8): 2350-2354,2359.

[10] Liu Ya-ya, Qin Ke-yun, Wang Ling. On similarity measures and distance measures of fuzzy soft sets[J]. Chinese Quarterly Journal of Mathematics, 2015, 30(3): 349-357.

[11]洪智勇.模糊软集之间的相似性度量及应用[J]. 计算机工程与应用, 2015, 51(12): 16-20.

[12]刘雅雅, 秦克云, 陈明奎. 软直觉模糊集的相似、距离和熵测度[J]. 济南大学学报:自然科学版, 2015, 29(6): 414-419.

[13] Atanassov K. Intuitionistic fuzzy sets[J]. Fuzzy sets and Systems, 1986, 20(1): 87-96.

[14] 王毅, 雷英杰. 基于包含度的直觉模糊相似度量方法[J]. 计算机工程与应用, 2008, 44(11): 16-18.

责任编校：孙 林

New Similarity Measures of Intuitionistic Fuzzy Soft Sets and Their Applications

WANG Jin-ying

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

The inclusion degrees of fuzzy soft sets are extended to intuitionistic fuzzy soft sets according to different cases of parameter set. And a new similarity measure of the intuitionistic fuzzy soft sets is proposed. First of all, the axiomatic definition of intuitionistic fuzzy soft sets and three different computational formulas are given with the inclusion degrees of intuitionistic fuzzy soft sets. Then the axiomatic definition of the similarity measure of intuitionistic fuzzy soft sets and the corresponding computational formulas are provided on the basis of the inclusion degrees of intuitionistic fuzzy soft sets. Finally the new similarity measure approach is applied to example analysis, and the effectiveness and feasibility is illustrated.

fuzzy implication operators; cardinal numbers set; intuitionistic fuzzy soft sets; inclusion degrees; similarity measures

10.15916/j.issn1674-3261.2017.03.015

O159；TP301

A

1674-3261(2017)03-0196-06

2016-05-16

国家自然科学基金项目(61473139)

王金项（1981-），女，辽宁黑山人，讲师，硕士。