三维power-normal分布的性质及参数估计问题的研究

2017-10-13孙丽红李树有

辽宁工业大学学报(自然科学版) 2017年3期

孙丽红，李树有

孙丽红，李树有

（辽宁工业大学理学院，辽宁锦州 121001）

应用了Clayton连接函数的性质给出了三维power-normal分布的分布函数及概率密度函数，并详细研究了三维power-normal分布的基本性质，同时，根据所构造出的三维power-normal分布模型，对其中的参数进行了最大似然估计的讨论。并给出了参数的最大似然估计的算法。结合费永法在文献中的1964年到1973年10年间长江大通站、淮河中渡站及黄河花园口站的天然年流经量数据作为样本数据，利用MATLAB程序计算了参数的最大似然估计。

power-normal分布；极大似然估计；Clayton连接函数；三维分布；MATLAB

Power-normal分布是一种斜正态分布[1]，它是正态分布的一种特殊情况。是在研究实际问题时正态分布[2]难以满足条件的情况下提出的一种新的研究方向，Isogai[3]在1999年第一次提到这类power-normal分布族。

Gupta等[4]在2008年正式提出了power-normal分布，用它来研究实线上的倾斜数据。Gupta等[5]在2013年根据一元power-normal分布一些基本性质详细研究了二元power-normal分布的相应性质。同时，根据直接估计和两步骤估计法对二元power-normal分布的参数进行了估计。

Nelsen[6]在1998年提出了Copula函数，并给出了其定义及基本的性质。本文在此基础上研究三维power-normal分布的性质及参数估计问题。

1 预备知识

1.1 Copula连接函数

Copula[7]函数是被用来将多维随机变量的联合分布用其一维边缘分布连接起来的函数，因此也常被称为“相依函数”或者“连接函数”，令，Copula函数表示为:，则有：

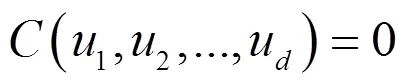
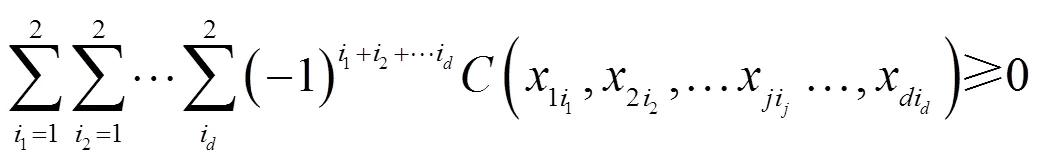
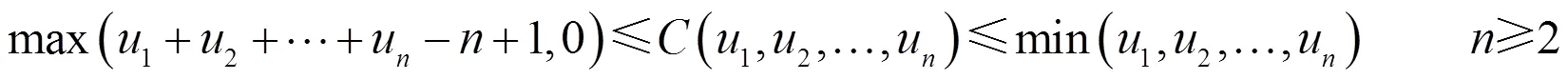
1.2 power-normal分布的参数估计问题

，

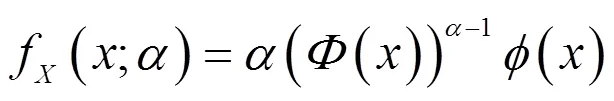
根据上式给出的power-normal分布的概率密度函数，得到其对数似然函数[8]为：

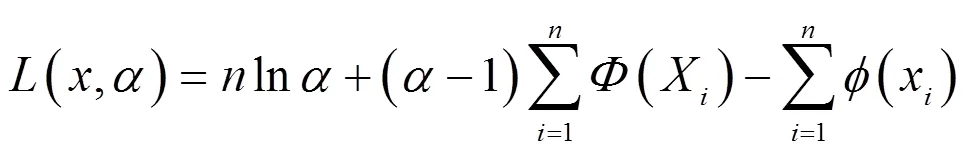
将上式对参数求导，并使其为零，得到参数的估计：

2 三维power-normal分布的参数估计

2.1 三维Clayton连接函数

Copula连接函数可分为椭圆Copula函数和阿基米德Copula函数两大类。其中，阿基米德Copula函数取生成元时，得到维Clayton copula连接函数的表达式为：。根据p维Clayton copula函数定义，当=3时，有三维Clayton copula函数：

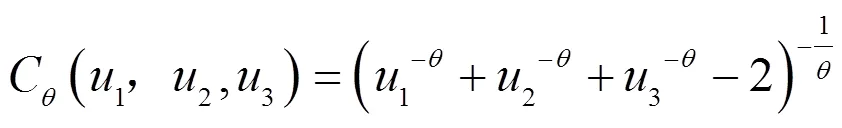
2.2 三维power-normal分布

2.2.1 三维power-normal分布定义

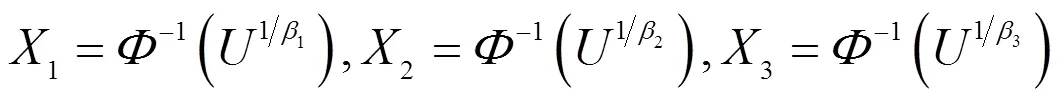
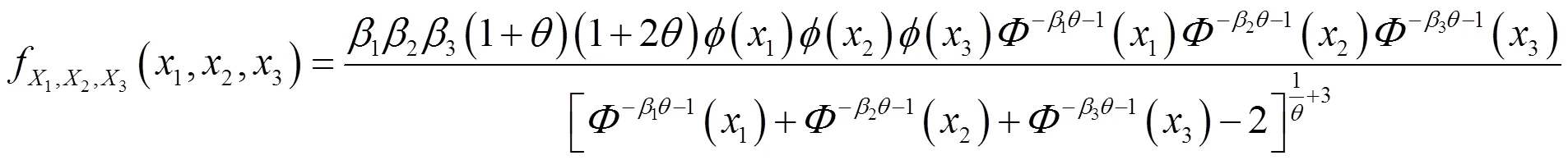
2.2.2 三维power-normal分布的性质

（2）联合分布函数

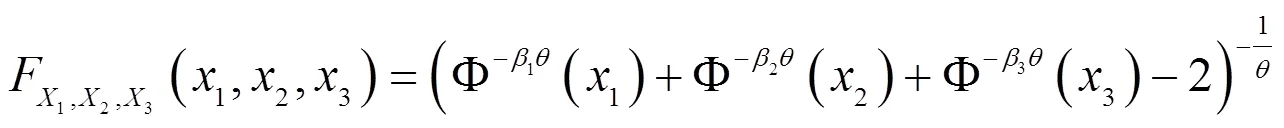
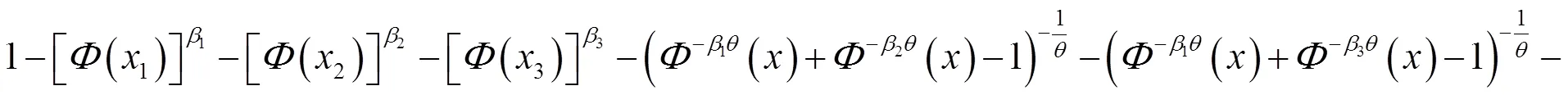
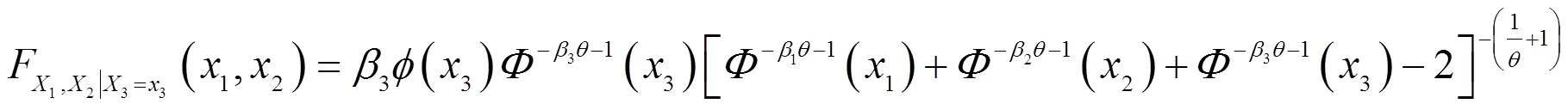
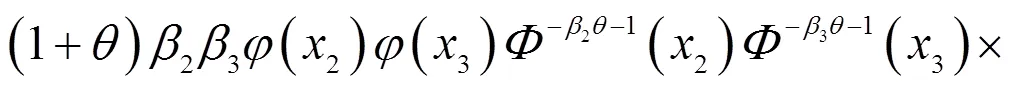
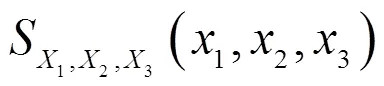
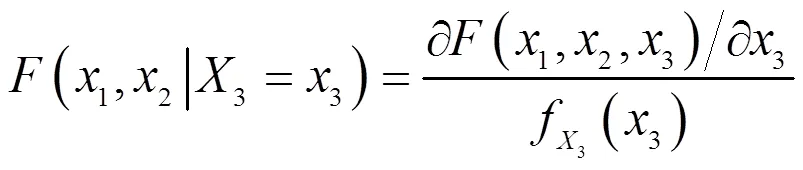
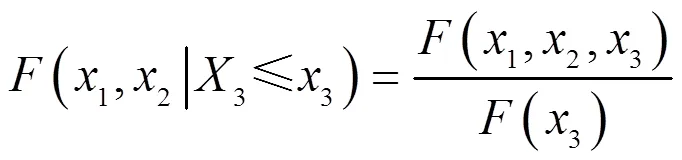
分别求在上述4种情况下的三维power-normal分布的条件概率分布函数。

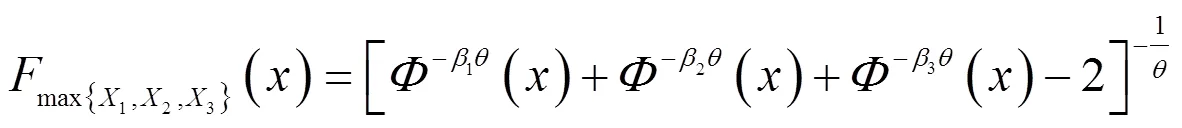
证明上述最大最小概率分布函数根据多维分布最大最小概率分布函数定义得到。

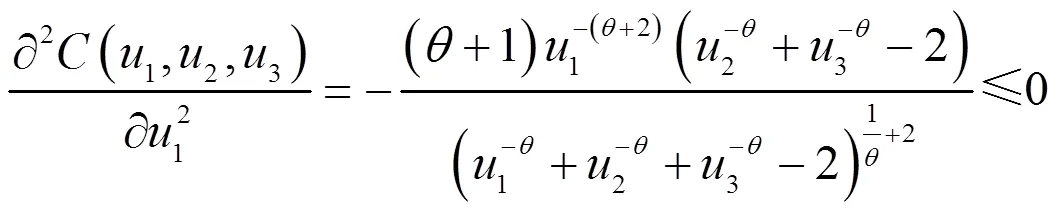
2.2.3 参数估计

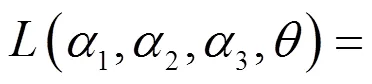
其中

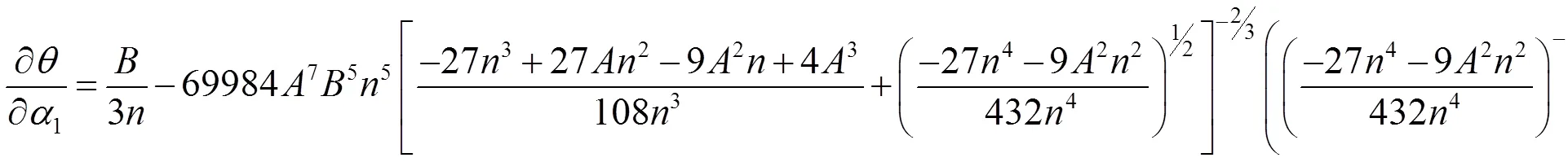
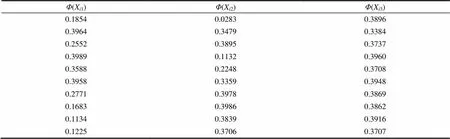
表1 整理数据

根据表2给出数据，可以发现对数似然方程组是一个三元方程组，且未知参数为。故可以应用MATLAB计算。得到参数，再根据参数的表达式可以得到参数，最后根据所设有。

3 总结

研究了三维power-normal分布及其参数估计问题，首先给出Copula函数的定义及基本性质，并根据一维power-normal分布的分布函数及概率密度函数，利用最大似然估计法给出未知参数的估计；其次，文章根据Copula函数的定义及性质，分析总结三维Clayton连接函数的基本性质，主要利用Clayton连接函数的性质及设变量的方法推导出三维power-normal分布的分布函数及概率密度函数，并给出其生存函数、条件概率密度函数、最大最小分布函数、单调性等基本性质和证明过程。同时，用最大似然估计法对其未知参数即连接函数中的参数、power-normal分布中的未知参数进行估计，并利用MATLAB给出参数估计值。若研究条件允许，研究内容可向多维方向扩展，其在经济学、统计学领域都将有广阔的研究前景。

[1] Azzalini A. A class of distributions which includes the normal ones[J]. Scandinavian journal of statistics, 1985: 171-178.

[2] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008.

[3] Isogai T. Power transformation of the F distribution and a power normal family[J]. Journal of Applied Statistics, 1999, 26(3): 355-371.

[4] Gupta R D, Gupta R C. Analyzing skewed data by power normal model[J]. Test, 2008, 17(1): 197-210.

[5] Kundu D, Gupta R D. Power-normal distribution[J]. Statistics, 2013, 47(1): 110-125.

[6] Nelsen R B. An Introduction to copulas (Lecture Notes in Statistics). 1998.

[7] 杨益党, 罗羡华. Copula 函数的参数估计[J]. 新疆师范大学学报: 自然科学版, 2007, 26(2): 15-18.

[8] Gupta R D, Gupta R C. Analyzing skewed data by power normal model[J]. Test, 2008, 17(1): 197-210.

[9] 费永法. 多元随机变量的条件概率计算方法及其在水文中的应用[J]. 水利学报, 1995(8): 60-66.

责任编校：孙林

Research on the Properties and Parameter Estimation Problem of Three-dimensional Power-normal Distribution

SUN Li-hong, LI Shu-you

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

In this paper, the cumulative distribution function and probability density function of three-dimensional power-normal distribution are given by using the properties of Clayton copula function. The basic properties of power-normal distribution are investigated in detail. At the same time, the maximum likelihood estimation of the parameters are discussed according to the three-dimensional power-normal distribution model. According to Fei Yongfa, who mentioned in the article, from 1964 to 1973 the annual flows data as the sample data among Datong station in the Yangtze River and the Huaihe River Ferry station and Huayuankou Station of the Yellow River, we use the MATLAB language to calculate the parameters of maximum likelihood estimation.

power - normal distribution; maximum likelihood estimation; clayton copula function; three-dimensional distribution; MATLAB

10.15916/j.issn1674-3261.2017.03.014

O212

1674-3261(2017)03-0190-06

2015-12-08

国家自然科学基金项目(11271064)

孙丽红(1991- )，女(满族)，辽宁抚顺人，硕士生。李树有(1964- )，男，吉林通化人，教授，博士。