基于核慢特征回归与互信息的常压塔软测量建模
2017-10-13蒋昕祎杜红彬李绍军
蒋昕祎,杜红彬,2,李绍军
基于核慢特征回归与互信息的常压塔软测量建模
蒋昕祎1,杜红彬1,2,李绍军1
(1华东理工大学化工过程先进控制与优化技术教育部重点实验室,上海200237;2中国石油天然气股份有限公司独山子石化研究院,新疆克拉玛依833699)
针对工业过程的非线性及动态特性,提出了一种新的慢特征回归软测量方法。该方法首先通过添加时延数据构造动态数据集,利用互信息最大化准则筛选变量从而减少信息冗余的影响。同时该方法在慢特征分析的基础上引入核函数扩展,加强模型处理非线性数据的能力,并将获得的核慢特征用于回归建模。核慢特征分析通过分析样本的变化,提取具有缓慢变化特征的成分,可以有效地刻画工业过程的变化趋势,提升回归模型精度。最后该方法的有效性在常压塔常顶油干点与常一线初馏点的软测量模型中得到了验证。
慢特征分析;互信息;动态建模;常压塔;石油;预测
引 言
在原油蒸馏过程中,常压塔顶及其侧线的油品质量都会受到初馏点、终馏点、干点等指标的影响。为了能实时测量并监控这些指标,可以使用在线分析仪或者人工离线分析的方法,但前者维护成本高、后者时滞大及精度低的问题都会影响产品质量。目前,许多学者利用软测量技术来解决此类问题,近年来数据储存及获取的便利使得数据驱动软测量方法得到了广泛应用。Shang等[1]将深度神经网络引入软测量建模,估计常压塔重柴油95%分馏点,通过半监督学习充分利用了工业数据,模型精度优于神经网络等方法。Li等[2]利用多核学习与核主元分析改进了最小二乘支持向量机,建立了常压塔航空煤油干点与闪点的软测量模型。Napoli等[3]针对小样本建模问题,通过样本重采样与噪声注入构成多个数据集,集成多个神经网络,证明了其在煤油冰点软测量建模中的有效性。其他算法如偏最小二乘法[4-5](partial least square,PLS)、主元回归[6](principal component regression,PCR)、高斯过程回归[7-8](gaussian process regression,GPR)等也广泛应用于软测量建模。
工业过程一般具有缓慢变化的动态特性,历史数据之间往往存在时间关联,历史数据也会影响模型构造,因此常会引入时延变量构造动态模型[9-10]。引入时延变量的新数据集包含了各变量的历史信息,使得后续构造的模型能更有效地利用历史数据中的隐藏信息。
为了能从数据中提取出有效信息,常用的特征提取方法有主成分分析、独立成分分析等。前者通过特征提取使得新成分的方差最大,后者通过特征提取使得新成分间的相关性最小,这两种方法都是从变量角度出发构造新的成分,但都未分析样本间的变化情况。Wiskott等[11]在2002年提出了慢特征分析(SFA),并将其应用于目标识别。与一般特征提取方法不同的是,SFA从样本的角度出发,分析样本的变化情况,提取出变化缓慢的新成分,反映过程数据的动态信息。近年来许多学者在其论文的基础上提出了改进算法并应用于模式识别[12-14]、盲源信号分离[15-16]、过程监控[17-19]等领域。文献[20-21]将其应用于质量指标预测与软测量建模,通过工业数据证明了慢特征回归(SFR)要优于传统的软测量方法。
慢特征回归可以有效地利用数据的动态特性,但是该方法是基于二项式扩展,处理非线性数据的能力较差,同时当模型的变量过多时,时延动态数据集的构造与二项式扩展方法必然会造成维数灾难问题,也可能导致过拟合的问题。因此,针对工业过程非线性与动态特性的问题,本文提出了一种新的慢特征回归方法,该方法在其基础上利用核函数扩展,加强模型处理非线性数据的能力。同时构造具有时延变量的动态数据集,为了避免出现信息冗余,分析各时延变量与主导变量间的互信息值,筛选变量进行核慢特征回归(kernel slow feature regression,KSFR)。常压塔的常顶油干点及常一线初馏点的软测量模型验证了本方法优于传统建模方法,具有更高的预测精度。
1 核慢特征回归
1.1 慢特征回归
慢特征回归(SFR)是一种基于慢特征分析的回归方法,主要分成两个部分:(1)慢特征分析;(2)慢特征线性回归。
1.1.1 慢特征分析 慢特征分析(SFA)是由Wiskott提出的一种在快速变化的时序数据中抽取缓慢变化特征的批量学习算法。SFA不仅能够得到全局最优解,而且其特征可以按照变化速率快慢依次提取。
现有训练数据tr={(),()}=1,2,…,n,慢特征分析的目标是要从现有的维输入数据矩阵()={1(),2(),…,x()}中提取到维变量()={1(),2(),…,T()},同时变量T()具有变化缓慢的特征。
为了从输入数据中提取慢特征,需要寻找一组映射函数()={1(),2(),…,f()},使得()=(())的每个变量尽可能变化缓慢,一般采用关于时间的一阶导数平方的均值来衡量变化速率。优化问题框架如下[22]

并满足以下3个条件
(2)
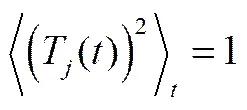
(4)
在线性情况下,慢特征的提取与主元提取类似,每个慢特征T()都是所有输入变量的线性组合T()=()。假设输入数据()已经标准化处理,那么式(1)、式(3)就可以写为
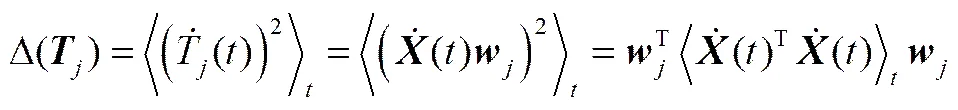
(6)
结合式(5)、式(6)可得
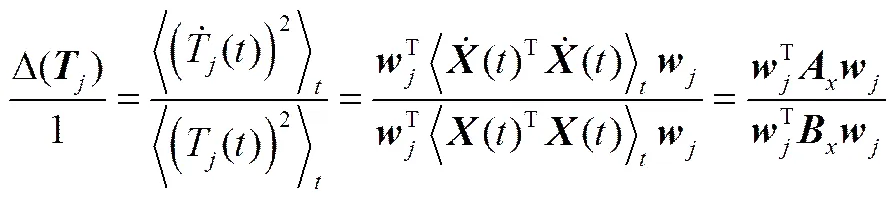
由式(7)可知,使其成立的权向量满足
W=W(8)
其中,=(1,2,…,w)为特征向量构成的特征矩阵,是由广义特征值1,2,…,构成的特征值对角阵,且1<2<…<。将w=Bw代入式(7)得
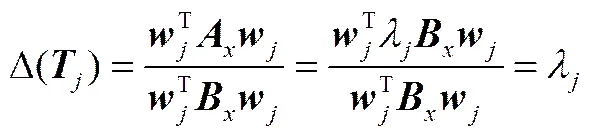
可以通过求解式的广义特征值,获得特征矩阵,映射输入数据获得慢特征。通常,这个优化问题的求解可以通过两步奇异值分解(SVD)来实现,推导流程如图1所示。具体分为以下4个步骤。
图1 SFA流程图
Fig.1 Flow chart of SFA
(1)标准化。首先将输入数据()={1(),2(),…,x()}标准化预处理,各变量的标准化结果为,构成标准化后的输入数据bz()={1bz(),2bz(),…,bz()},其中={1,2,…,}与={1,2,…,}分别是输入数据的均值向量以及标准差阵。为了公式简化,下文用()表示已经标准化后的数据。
(2)非线性扩展及中心化。接着对输入数据()进行非线性扩展。考虑到非线性问题,在预处理时通常需要非线性扩展,SFA采用的是二次多项式扩展
()=(())={1,…,x,11,12,…,xx} (10)
这样维输入数据通过二项式扩展(•)变成了维,其中。然后对扩展后的数据()进行中心化,构成中心化后的输入数据c()=()-,其中是各变量的均值向量。为了公式简化,下文用()表示经过非线性扩展与中心化的输入数据。
(3)白化处理。为了能满足式(3)、式(4)的条件,继续对()进行白化处理。白化处理可以使各变量不相关,同时为单位方差。定义=〈()T()〉表示()的协方差阵,由SVD可知=UT,白化矩阵=-1/2T,白化后的数据为
()=()T=()-1/2(11)
因此,可得〈()T()〉=。将()=()T与=〈()T()〉代入
ST=(12)

需要注意这里会出现=diag{1,2,…,}里的特征值极小的情况。白化的一个作用就是去相关,因此本文设置阈值=1×10-7与比较,舍弃小于的特征值,从而实现降维。
(4)求取映射向量及相应慢特征。上面几个步骤已经把变量进行了预处理,使其满足单位方差、零均值以及互不相关,同时也实现了非线性扩展,最后确定映射向量,按照式(8)可得
w=Bw(14)
由于可能会出现非满秩情况,直接用广义特征值求映射向量会出现计算错误,故需要白化处理将问题转换成一般特征值求解[22]。
将式(14)左乘白化矩阵
w=SBw(15)
将式(12)、式(13)与T(T)-1=代入式(15)可得
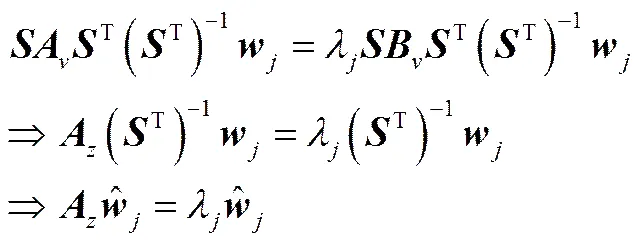
通过这几步代换,只需要一般SVD就可求出矩阵,即的协方差阵的特征向量,从而得到慢特征映射向量
(17)
最后,利用映射得到第个慢特征T()=()。由式(9)可知,慢特征变化快慢由矩阵的特征值决定,因此第一慢特征的映射向量1就是矩阵最小特征值1对应的特征向量与T的乘积,然后第二慢特征的映射向量2就是第二小特征值2对应的特征向量与T的乘积,依次类推可得其他慢特征。
1.1.2 慢特征回归 获得维慢特征()={1(),2(),…,T()}后,通过最小二乘回归求出输出向量()与维慢特征()的回归系数,最后利用回归系数就可以预测新输入数据的对应输出。
1.2 核慢特征回归(KSFR)
慢特征分析在数据预处理阶段,为了加强算法处理非线性数据的能力,一般会采用多项式扩展的方法,但当数据维数过多时,多项式扩展会导致维数灾难问题,严重影响运算速度与精度,而且这种扩展并不能显著提高算法处理非线性数据的能力,特别是对于一些复杂的工业过程,其高维数据之间往往存在很强的非线性,这时多项式扩展的弊端就会凸显出来。
核技巧(kernel trick)是一种处理非线性数据的方法,它通过非线性变换将低维空间的样本映射到高维特征空间,只要选取合适的非线性变换,就能将原输入空间的非线性问题转化为高维特征空间中的线性或近似线性问题。经过非线性映射,数据集得到以下变换

为了克服维数灾难,需要引入核函数。对任意的与均满足(x,x)=K,j=()T(),即将高维空间的内积运算转化为输入空间的核函数运算。高维矩阵=T中的每个元素都用核函数表示,称其为核矩阵[23]
(19)
常用的核函数有多项式核函数、指数型核函数、高斯径向基核函数等,本文采用学习能力强的高斯径向基核函数
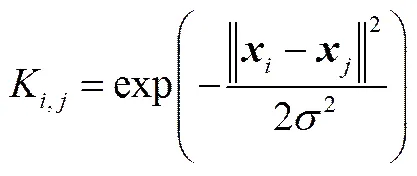
这样,利用核函数替代多项式扩展从而加强算法处理非线性数据的能力,实现核慢特征回归。其主要改进在非线性扩展部分,用核函数扩展的数据替代非线性扩展的(),这样对应的优化目标就是[24]
(21)
同时求解映射向量的广义特征值问题就转换为
W=W(22)
核慢特征回归(KSFR)的具体步骤如下。
(1)训练部分tr={(),()}=1,2,…,n
① 标准化,获得标准化后的数据{(),()},均值,及标准差,。
③确定与,获得的白化矩阵,分别求得白化后的数据与,利用白化实现降维
=T(23)
=AST(24)
④ 求取的特征向量,并转换为映射向量,映射得到慢特征
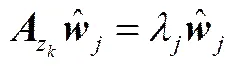
(26)
=(27)
⑤利用最小二乘法求得慢特征与标准化的输出数据间的回归系数=(T)-1。
(2)测试部分te={te()}=1,2,…,n
① 利用与标准化测试数据。
③ 利用映射向量,获得慢特征te
te=te(28)
④ 预测测试数据输出值′p=te。
⑤ 反标准化,获得最终预测值p。
利用核函数扩展改进慢特征回归提升了算法处理非线性数据的能力,同时也避免了多项式扩展的维数灾难问题,可以提升算法性能。
2 动态建模与互信息变量选择
在工业过程中,各变量数据的采集一般都是按照固定时间进行的,各采样点间存在明显的时间相关性,当前时刻的数据并不能完全刻画过程的动态信息。因此为了获得工业过程数据的动态信息,考虑历史数据对于当前的影响,可以引入时延变量数据构造动态数据集。
原数据集为={(),()}=1,2,…,n,其中()={1(),2(),…,x()},输入变量共有维,每个变量有个样本。引入时延阶数,就可以构造动态数据集,输入变量变成了(+1)维,即()≡{(),(-1),(-2),…,(-)}。动态数据集的构造使得模型趋于动态,有利于分析工业数据,但是同样也造成了维数过大的问题,过多的时延变量会导致信息冗余,最后可能会发生过拟合问题。因此,可以通过变量选择进行降维处理[25]。本文采用互信息(mutual information,MI)。
互信息能够反映两个变量之间的统计依赖程度,其定义来源于信息论中熵的概念。熵也称作信息熵或Shannon熵,通过数值形式来表达随机变量取值的不确定性程度,从而描述相应变量的信息含量大小。变量的信息熵定义如式(29)所示,其中()为的概率密度分布函数。

互信息表示的是两个随机变量之间的关联程度,即给定一个随机变量后,另一个随机变量不确定性的削弱程度。
(30)
其中,p(),p()和p,y(,)分别是变量与的边缘概率密度函数以及联合概率密度函数。可以通过核密度估计或者直方图法来估计密度函数。核密度估计虽然估计精度较高,但是需要选择核函数以及设置带宽;直方图法则实现简单,只需要等间隔地划分变量与的数据构成的二维平面,判断符合子区间的样本个数,从而依次确定边缘以及联合概率密度函数[26]。
当变量与是相互独立或者完全无关时,互信息(,)等于0,即两变量之间不存在共同拥有的信息。当变量与相互依赖程度很高时,互信息(,)会很大,即两变量之间存在较多的共同信息[27-28]。基于互信息的变量选择准则有很多[29],本文采用的互信息最大化准则,即通过比较不同变量与因变量间的互信息值,从中选择互信息较大的变量作为具有统计相关性的有效变量。
3 基于DMI-KSFR的软测量方法
基于核慢特征回归与互信息的软测量建模流程如图2所示。
(1)在原始训练数据的维输入tr()的基础上引入时延阶数,构造(+1)维动态数据集d_te()≡{tr(),tr(-1),tr(-2),…,tr(-)},使得数据集包含各变量的历史信息,充分考虑过程的动态性,同时对测试数据输入te()构造相同时延阶数的动态数据集d_te()。
(2)针对动态数据集的第(=1,2,…,+)个维变量,计算其与训练数据输出tr间的互信息
MI,y=(x,tr) (31)
将这MI,y∈1×(kd+k)个互信息值降序排列,选择前个最大值对应的变量,构成动态互信息输入数据集DMI_tr()∈×NC。同时对测试数据的动态数据集te()选择相同的变量构造DMI_te()。
(3)对动态互信息输入数据集DMI_tr(),进行核慢特征分析,获得各个核慢特征的权向量以及各核慢特征tr,j,同时利用训练获得的权向量构造测试数据的核慢特征te,j。
(4)对得到的核慢特征tr和训练数据输出tr建立最小二乘回归模型,获得模型回归参数=(Ttrtr)-1trtr。最后利用回归参数估计测试数据的输出p。
4 常压塔质量指标软测量建模研究
常压蒸馏塔是炼油企业的首要生产装置,其生产水平的高低直接影响着原油的利用率和企业的经济效益。作为一种典型的多侧线采出蒸馏塔,常压塔从侧线分别抽出煤油、汽油、柴油等产品。这些侧线馏分经汽提塔提出轻组分,经换热回收一部分热量分别冷却后送出装置。塔底未经汽化的重油经过热水蒸气提出轻组分后,作减压塔进料。为了使塔内各部分的汽、液负荷比较均匀,并充分利用回流热,在塔中各侧线抽出口之间打入中段循环回流[30]。
常压塔馏出产品需要控制以下质量指标:常顶油(石脑油)的干点,常一线油(汽油)的闪点、冰点、馏程,柴油的凝点、95%馏出温度等。本文分析的是常顶油干点以及常一线初馏点。干点和初馏点都是油品的重要质量指标,初馏点会影响到本侧线油品的质量与上一侧线油品的收率。干点则会干扰本侧线的产品质量与下一侧线的馏分收率[31]。本文利用基于核慢特征回归与互信息的方法分别对常顶油干点和常一线初馏点进行软测量建模。
本文使用了两个指标来评判算法性能,分别是均方根误差(RMSE)与可决系数(2)
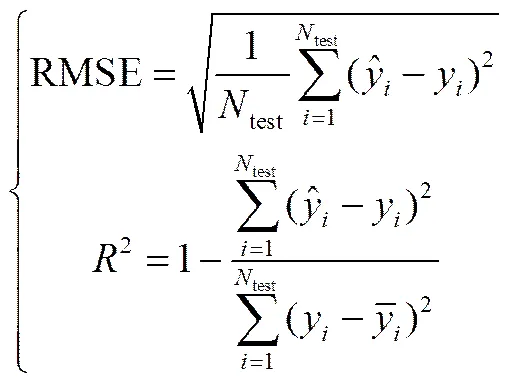
4.1 某常压塔常顶油干点软测量建模
常压塔顶部的主要产品是常顶油,常顶油经过脱丁烷塔后生成石脑油。常顶油的干点越高,会导致其产出油品的重组分过高,影响其油品质量,使得后续生成的石脑油中芳烃含量过高,不适于裂解反应,影响乙烯、丙烯等产量。为了建立常顶油干点的软测量模型,本文选择6个辅助变量,分别是常顶压力、常顶温度、回流温度、采出比、常顶循流量和常一、二、三线的采出量。常顶油干点数据集总共有500组样本,前400组用于模型训练,后100组用于模型效果测试。
本方法需要设置的参数是动态数据集的时延阶数、互信息最大化选择的变量个数以及高斯核函数的核宽度。本文对训练数据集采用十折交叉验证设置阶数=1,这样总的变量就有6×(1+1)=12个,并通过互信息的方法选择11个相关变量,具体比较见图3。通过多次试验设置高斯核宽度为450。
首先,观察提取到的核慢特征的情况。图4、图5分别是训练数据与测试数据中提取到的前4个变化最缓慢的核慢特征,可以发现每个核慢特征的变化情况都不同。纵向比较各核慢特征,可以发现第一核慢特征变化最缓慢,而越到后面的特征变化越快。横向比较训练数据与测试数据的核慢特征,可以发现两者的变化趋势基本是一致的,具有相同的变化频率。因此核慢特征分析可以有效地提取到变化缓慢的信息。
为了验证本方法的有效性,需要纵向比较几点改进对于模型性能的影响,选择以下方法。
(1)慢特征回归SFR,采用非线性扩展。
(2)动态慢特征回归(dynamic SFR,DSFR),通过动态建模构造数据集后,采用非线性扩展。
(3)核慢特征回归(KSFR),采用核函数扩展的慢特征回归。
(4)动态核慢特征回归(dynamic KSFR,DKSFR),通过动态建模构造数据集后,采用核函数扩展的慢特征回归。
(5)本方法DMI-KSFR,通过动态建模与互信息变量选择构造数据集后,采用核函数扩展的慢特征回归。
图6是不同方法的预测值与实际值的比较,图中各点横坐标表示的是预测值,纵坐标表示的是实际值,数据点离对称轴虚线越近,则表示预测效果越好。分析图6和表1可以发现,本文的几点改进可以提高模型性能。引入动态建模的思想,可以从动态角度分析工业数据,提高模型精度;利用核函数扩展替代原有的二项式扩展,可以加强模型处理非线性数据的能力;加入互信息变量筛选,可以剔除动态建模造成的变量冗余问题,进一步提高模型精度。RMSE与2的提升表明后续改进提升了模型的拟合程度。
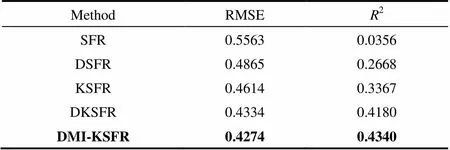
表1 不同方法的比较
图7是本方法对于测试数据的预测效果。分析图7与图5可以发现,整体数据具有一定的周期性,使得图6存在数据点处于同一水平线,即这些点的实际值都是相同或近似的。本方法获得的预测值与实际值构成的数据点离中心虚线最近,因此本方法可以有效地提升模型的预测精度。
4.2 某石化常压塔初馏点软测量建模
某石化炼油装置常一线的主要产品是汽油。常一线初馏点过低,会使其轻组分过高,影响本侧线的油品质量,同时影响上一侧线的油品收率。因此需要通过软测量建模实时分析常一线初馏点指标,保证工况正常运行。
为了建立常一线初馏点的软测量模型,本文选择11个辅助变量,分别是常顶回流量、常顶循流量、常一中流量、常压塔塔底汽提蒸汽量、汽提塔塔顶温度、重沸器出入口温度、常一中油出入口温度、汽提塔油气温度、常一线汽提塔出口温度等。本数据集共有135组样本,样本采样间隔为1 h。本文选择前100组数据作为训练数据,后35组数据作为测试数据。
这里需要设置的参数还是时延阶数、互信息选择的变量个数以及高斯核宽度。本文对训练数据集采用十折交叉验证设置阶数=2,这样总的变量就有11×(2+1)=33个,并通过互信息的方法选择31个相关变量,具体比较见图8。通过多次试验设置高斯核宽度为470。
为了分析本方法的优越性,与其他传统建模方法进行横向比较,选择以下方法。
(1)动态慢特征回归(DSFR),通过动态建模构造数据集后,采用非线性扩展的慢特征回归。
(2)反向传播神经网络(back propagation neural network,BPNN)。
(3)动态核偏最小二乘回归(dynamic KPLS,DKPLS),通过动态建模构造数据集后,采用KPLS回归。
(4)核慢特征回归(KSFR),采用核函数扩展的慢特征回归。
(5)本方法DMI-KSFR。
图9是各方法预测值与实际值的比较。分析图9与表2可以发现,本文方法与BP神经网络,DKPLS以及DSFR等传统方法相比,具有一定的提升。DSFR采用动态建模的思路,但是没有使用有效的非线性扩展方法,故效果最差;BP神经网络的非线性拟合能力较好,但是没有考虑数据的动态特性;DKPLS虽然运用了核函数扩展,但是KPLS方法也没有考虑动态特性;本方法在KSFR核函数扩展的基础上采用动态数据集以及互信息变量选择,提升了算法性能。
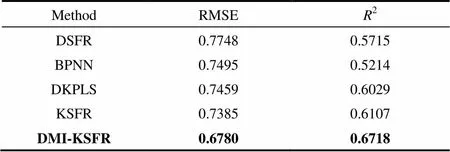
表2 不同方法的比较
图10是本方法对于测试数据以及全部数据的预测效果,其中小图是全部135组样本的预测效果,可以发现尽管从第120个样本点开始数据变化趋势与之前不同,但是本方法仍能有效地预测出常一线初馏点的趋势,并获得了不错的效果。
5 结 论
本文提出了一种基于核慢特征回归的软测量建模方法,并应用于具有非线性和动态特性的工业过程。动态数据集的构造以及互信息变量筛选使得用于建模的数据不仅具有动态信息而且避免了信息冗余的问题;核函数扩展使得慢特征分析处理非线性数据的能力得到了显著的提升。核慢特征可以更好地刻画复杂工业数据的变化趋势,提高回归模型的精度。常顶油干点与常一线初馏点软测量建模的实验结果表明本方法具有较好的预测效果,与传统方法相比也有一定的提升。
References
[1] SHANG C, YANG F, HUANG D,. Data-driven soft sensor development based on deep learning technique[J]. Journal of Process Control, 2014, 24(3): 223-233.
[2] LI Q, DU Q, BA W,. Multiple-input multiple-output soft sensors based on KPCA and MKLS-SVM for quality prediction in atmospheric distillation column [J]. International Journal of Innovative Computing, Information and Control, 2012, 8(12): 8215-8230.
[3] NAPOLI G, XIBILIA M G. Soft sensor design for a topping process in the case of small datasets[J]. Computers & Chemical Engineering, 2011, 35(11): 2447-2456.
[4] GALICIA H J, HE Q P, WANG J. A reduced order soft sensor approach and its application to a continuous digester[J]. Journal of Process Control, 2011, 21(4): 489-500.
[5] 袁小锋, 葛志强, 宋执环. 基于时间差分和局部加权偏最小二乘算法的过程自适应软测量建模[J]. 化工学报, 2016, 67(3): 724-728. YUAN X F, GE Z Q, SONG Z H. Adaptive soft sensor based on time difference model and locally weighted partial least squares regression[J]. CIESC Journal, 2016, 67(3): 724-728.
[6] YUAN X F, HUANG B, GE Z Q,. Double locally weighted principal component regression for soft sensor with sample selection under supervised latent structure[J]. Chemometrics & Intelligent Laboratory Systems, 2016, 153: 116-125.
[7] YU J, CHEN K, MORI J,. A Gaussian mixture copula model based localized Gaussian process regression approach for long-term wind speed prediction[J]. Energy, 2013, 61(6): 673-686.
[8] YANG K, JIN H P, CHEN X G,. Soft sensor development for online quality prediction of industrial batch rubber mixing process using ensemble just-in-time Gaussian process regression models[J]. Chemometrics & Intelligent Laboratory Systems, 2016, 155: 170-182.
[9] 刘国海, 苏勇, 杨铭, 等. 基于多准则和高斯过程回归的动态软测量建模方法[J]. 东南大学学报(自然科学版), 2015, (6): 1086-1090. LIU G H, SU Y, YANG M,. Dynamic soft sensor modeling based on multi-criterion method and Gaussian process regression [J]. Journal of Southeast University (Natural Science Edition), 2015, (6): 1086 -1090.
[10] 阮宏镁, 田学民, 王平. 基于联合互信息的动态软测量方法[J]. 化工学报, 2014, 65(11): 4497-4502. RUAN H M, TIAN X M, WANG P. Dynamic soft sensor method based on joint mutual information [J]. CIESC Journal, 2014, 65(11): 4497-4502.
[11] WISKOTT L, SEJNOWSKI T. Slow feature analysis: unsupervised learning of invariances[J]. Neural Computation, 2002, 14(4): 715- 770.
[12] WU C, DU B, ZHANG L. Slow feature analysis for change detection in multispectral imagery[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(5): 2858-2874.
[13] FRANZIUS M, WILBERT N, WISKOTT L. Invariant object recognition and pose estimation with slow feature analysis[J]. Neural Computation, 2011, 23(9): 2289-2323.
[14] ZHANG Z, TAO D. Slow feature analysis for human action recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(3): 436-450.
[15] MINH H Q, WISKOTT L. Multivariate slow feature analysis and decorrelation filtering for blind source separation.[J]. Image Processing IEEE Transactions on, 2013, 22(7): 2737-2750.
[16] 何会会, 李钢虎, 要庆生, 等. 用慢特征分析算法实现水声信号盲分离[J]. 声学技术, 2014, 33(3): 270-274. HE H H, LI G H, YAO Q S,.Blind source separation of underwater acoustic signals by using slowness feature analysis[J].Technical Acoustics, 2014, 33(3): 270-274.
[17] SHANG C, HUANG B, YANG F,. Slow feature analysis for monitoring and diagnosis of control performance[J]. Journal of Process Control, 2016, 39: 21-34.
[18] SHANG C, YANG, GAO X Q,. Concurrent monitoring of operating condition deviations and process dynamics anomalies with slow feature analysis[J]. AIChE Journal, 2015, 61(11): 3666-3682.
[19] ZHANG H Y, TIAN X M, CAI L F. Nonlinear process fault diagnosis using kernel slow feature discriminant analysis[J]. IFAC-Papers on Line, 2015, 48(21): 607-612.
[20] SHANG C, YANG F, GAO X Q,. Extracting latent dynamics from process data for quality prediction and performance assessmentslow feature regression[C]// American Control Conference (ACC). Chicago: IEEE, 2015: 912-917.
[21] SHANG C, HUANG B, YANG F,. Probabilistic slow feature analysis-based representation learning from massive process data for soft sensor modeling[J]. AIChE Journal, 2015, 61(12): 4126-4139.
[22] KONEN W, KOCH P. The slowness principle: SFA can detect different slow components in non-stationary time series[J]. International Journal of Innovative Computing & Applications, 2011, 3(3): 3-10.
[23] 王桂增, 叶昊. 主元分析与偏最小二乘法[M].北京: 清华大学出版社, 2012: 106-107. WANG G Z, YE H. Principal Component Analysis and Partial Least Squares [M].Beijing: Tsinghua University Press, 2012: 106-107.
[24] BOHMER W, GRUNEWALDER S, NICKISCH H,. Generating feature spaces for linear algorithms with regularized sparse kernel slow feature analysis[J]. Machine Learning, 2012, 89(1/2): 67-86.
[25] SOUZA F, SANTOS P, ARAUJO R. Variable and delay selection using neural networks and mutual information for data-driven soft sensors [C]// Emerging Technologies and Factory Automation (ETFA).Spain: IEEE, 2010: 1-8.
[26] MODDEMEIJER R. On estimation of entropy and mutual information of continuous distributions[J]. Signal Processing, 1989, 16(3): 233-248.
[27] 童楚东, 蓝艇, 史旭华. 基于互信息的分散式动态PCA故障检测方法[J]. 化工学报, 2016, 67(10): 4317-4323.TONG C D, LAN T, SHI X H.Fault detection by decentralized dynamic PCA algorithm on mutual information[J].CIESC Journal, 2016, 67(10): 4317-4323.
[28] JIN H P, CHEN X G, YANG J W,. Adaptive soft sensor modeling framework based on just-in-time learning and kernel partial least squares regression for nonlinear multiphase batch processes[J]. Computers & Chemical Engineering, 2014, 71: 77-93.
[29] BOLN-CANEDO V, SNCHEZ-MAROO N, ALONSO-BETANZOS A. Feature Selection for High-Dimensional Data[M]. Springer Publishing Company, Incorporated, 2015: 17-24.
[30] 金思毅, 李悦卿, 夏茂森. 常减压装置常压塔塔顶汽油干点的软测量[J]. 化工进展, 2006, 25(s1): 74-76. JIN S Y, LI Y Q, XIA M S. Curde colmun gasoline end point soft-sensing of atmospheric and vacuum unit[J].Chemical Industry and Engineering Progress, 2006, 25(s1): 74-76.
[31] 唐孟海, 胡兆灵. 原油蒸馏[M]. 北京: 中国石化出版社, 2007: 44-45. TANG M H, HU Z L.Crude Oil Distillation [M]. Beijing: China Petro-Chemical Press, 2007: 44-45.
Atmospheric tower soft sensor based on regression and mutual information of kernel slow features
JIANG Xinyi1, DU Hongbin1,2, LI Shaojun1
(1Key Laboratory of Advanced Control and Optimization for Chemical Processes (Ministry of Education), East China University of Science and Technology, Shanghai 200237, China;2Research Institute of Petro China Dushanzi Petrochemical Company, Karamay 833699, Xinjiang, China)
A novel soft sensor method based on slow feature regression (SFR) was proposed for industrial process with nonlinear and dynamic characteristics. First, a dynamic dataset was built by adding time-delay data and information redundancy was reduced by selecting variables according to mutual information maximization criteria. Then, kernel function was introduced into slow feature analysis(SFA)to improve capability of processing nonlinear data and the kernel slow features were used for regression. Through analysis of sample variation, kernel slow feature analysis(KSFA)could extract components with slowly varying dynamics, characterize trend of industrial process effectively, and improve precision of regression modelling. Finally, effectiveness and feasibility of the proposed method were verified by soft sensor model of constant top oil dry point and constant first line dropping point in atmospheric tower.
slow feature analysis; mutual information; dynamic modeling; atmospheric tower; petroleum; prediction
10.11949/j.issn.0438-1157.20161395
TP 274
A
0438—1157(2017)05—1977—10
李绍军。
蒋昕祎(1993—),男,硕士研究生。
国家自然科学基金项目(21676086,21406064)。
2016-09-29收到初稿,2017-01-22收到修改稿。
2016-09-29.
Prof.LI Shaojun, lishaojun@ecust.edu.cn
supported by the National Natural Science Foundation of China (21676086,21406064).
