基于FPGA的多cell腔的场平坦度控制

张志刚 赵玉彬 徐 凯 郑 湘 李 正 赵申杰 常 强 侯洪涛 刘建飞



基于FPGA的多cell腔的场平坦度控制

张志刚1,2赵玉彬1,2徐 凯1,2郑 湘1,2李 正1,2赵申杰1,2常 强1,2侯洪涛1,2刘建飞1,2

1（中国科学院上海应用物理研究所嘉定园区 上海201800）2（上海市低温超导高频腔技术重点实验室 上海201800）

在多cell腔的场平坦度控制处理中，最重要的算法为除法运算，而传统整数除法算法采用多次相减和移位的方法来实现，其算法存在以下缺点：相减运算消耗大量时钟即“吃时钟”、每完成一次算法所需时钟周期不固定以及此算法在实际工程中不能有效工作。针对传统整数除法器的弊端，提出一种基于现场可编程门阵列(Field-Programmable Gate Array, FPGA)的循环型不可恢复除法器。设计的循环型不可恢复除法器通过改善程序结构和优化时序，实现除法运算速度的提高和固定运算所需时钟周期的目的。此算法通过QuartusII编译和综合，以及仿真工具ModelSim的仿真验证，达到预期功能效果，同时在上海光源增强器高频数字低电平控制器中被采用，实现场平坦度稳定度在±1.3%以内，完成每次运算所需35个时钟周期，优于设计指标。

现场可编程门阵列，循环型，除法器，场平坦度控制，时钟周期

随着加速器对高能量和高性价比的要求，多cell高频腔得到发展及应用。在多cell高频腔的控制中，为保障腔体的正常工作，高频低电平控制器除了包含频调环路控制外，还需要增加场平坦度控制。同时，数字技术得到快速发展，低电平控制技术也基本实现数字化，例如：上海光源(Shanghai Synchrotron Radiation Facility, SSRF)增强器高频数字化低电平控制器[1]、欧洲自由电子激光(European X-ray Free-Electron Laser, European XFEL)数字高频控制器[2]等。

以SSRF的增强器高频系统（图1）为例引入多cell腔的控制，此系统主要包含低电平控制器(Low Level Radio Frequency, LLRF)、高频功率源(Klystron)、功率分配器(Magic T)、两台5-cell常温腔（Cavity#1和Cavity#2）和传输系统[3‒4]。在5-cell常温腔的第2个cell和第4个cell处安装有步进马达，主要用于腔的频率和场平坦控制，场平坦度的计算如式(1)[1,3]：

数字低电平控制器主要采用的是数字同向/正交/(In-phase/Quadrature)技术[5‒6]。

图1 上海光源增强器高频系统框图

Fig.1 Layout of the radio frequency system of SSRF booster.

在场平坦度控制算法中，除法作为最重要的运算影响控制器的整体性能。除法是四则基本运算里面最繁杂的，也是最难实现的。特别是在现场可编程门阵列(Field-Programmable Gate Array, FPGA)的算法设计中，除法器的运算精度、运算速度和预知运算所占时钟周期对系统的整体性能具有较大影响。目前，实现除法器的方法主要有两种：硬件实现和软件实现。硬件实现的方法主要通过将被除数寄存器的内容不断地向除数的最高位移动来完成除法运算，以耗费硬件资源为代价，来实现高速计算的特点；件实现除法器算法主要是通过“减并移位”的思想来实现，即从被除数中重复地减去除数，直到已检测到余数小于除数为止，这样可以通过累计减法运算的次数而得到商，而余数是在减法运算结束时被除数中的剩余值。软件实现除法器算法进一步提高器件的工作频率和设计的灵活性，可以从总体上提高设计性能。因此，设计一种基于Verilog的硬件描述语言(Hardware Description Language, HDL)且运算速度快和预知运算所占时钟周期的循环型除法器，在FPGA数据处理中具有很重要的实际意义和工程价值。

1 除法器算法原理

循环型除法器也称位操作除法器，算法主要包含移位、相减和比较三种操作，通过此三种操作实现求商和余数。

假设给定比特自然数（被除数）与比特整数（除数）[7]，也即：0≤<2和0≤<2。则除以的整数除法器可以表示为：

∙()(2)

式中：为除法运算的商；为除法运算的余数。并且都为自然数。

在进行除法运算时，首先须将被除数与除数对齐。采用¢=2∙来替代，则精度为的除法可以写为：

2∙=∙′′ (′<′) (3)

或者是：

=∙′∙2+R′∙2=∙′∙2

(=′/2<′) (4)

为了减少运算过程中的位宽，式(4)可以用′=/2来替代，用′=2−1∙来替代。相应的迭代过程为：

其中：(0)=。式(4)可以写成下面的方程：

∙2[(1)∙2−1(2)∙2−2()∙20]∙() (6)

因此：

=(1)∙2−1(2)∙2−2()∙20(7)

′=() (8)

2 除法器算法设计

除法器有操作简单的传统除法器和优化设计的循环型除法器，传统除法器主要是通过递减和比较两种操作实现求商和余数，而循环型除法器通过移位、相减和比较三种操作实现求商和余数[8‒10]。

2.1 传统除法器算法设计

传统除法器的设计相对简单，主要是采用下列步骤：1) 初始化，包括：获取除数(Divisor)和被除数(Dividend)的正负关系、正值化被除数和除数、商数递增（被除数与除数递减）、正值化除数；2) 递减()结束：当正值化被除数小于正值化除数时，递减过程剩下的是余数，且带入被除数的正负关系；3) 判断输出的结果正负关系：根据除数和被除数的正负关系决定商(Quotient)和余数(Reminder)的符号。传统除法器算法设计流程框图如图2所示。

图2 传统型除法器算法设计流程图

虽然传统除法器的设计和实现较为简单，但是当被除数和除数相差较大时，整个除法运算所消耗的时钟周期较多的弊端就会显露出来，其不仅影响算法的运算速度，而且每次算法所耗时钟周期不固定，对整个系统的性能带来影响，实际用途较低。故提出一种基于Verilog HDL的循环型恢复除法器，此除法器通过改善程序结构和优化时序，能提高除法运算速度，同时具有预知每次除法运算所需的时钟周期的特点。

2.2 循环型除法器算法设计

循环型除法器也叫位操作除法器，典型的循环型除法器可分为可恢复和不可恢复，可恢复是指满足特定条件后，运算空间得到释放，恢复到初始化的状态，反之则相反。实验时采用控制简便、逻辑清晰的不可恢复循环型除法器。

为方便讨论，假设被除数Dividend为位和除数Divisor为(≤)位，则运算空间就有+−1，[−1:0]为正值化的被除数Dividend，[+−1:−1]作为除数减法运算。为了便于减法运算，创建位数为+1的空间用于存储除数Divisor的负值补码。同时，为保证运算结果准确，还需要研究同步运算，使[+−1:−1]和[−1:0]的减法在别的运算空间中进行，命名为空间，空间与空间具有相同的位宽，即用[+−1:0]表示。

循环型除法器算法的运算流程如下：1)空间被赋予“[+−1:−1]+”；2) 判断[+−1:0]的最高位，即符号位是逻辑1还是逻辑0，如果为1则表示[+−1:−1]的值小于正值化除数，[+−1:0]左移一位并补0。否则表示[+−1:−1]的值大于正值化除数，空间被赋予空间的值，并且左移一位补1。循环次数用表示，具体流程如图3所示。

图3 循环型除法器运算流程图

3 程序设计

针对图2、3分别用Verilog HDL硬件描述语言编程，为便于讨论，假设被除数为32位带符号数，除数为16位带符号数，其程序系统模块图如图4所示，其中Clk为系统时钟信号，Rst为复位信号，Start_flag为除法器算法启动信号，Dividend[31:0]为32位被除数，Divisor[15:0]为除数，Done_flag为除法器算法完成信号，Quotient[15:0]为除法器运算得到的商，Reminder[15:0]为除法器运算得到的余数，Sq_diff[47:0]和Sq_temp[47:0]为循环型除法器运算所拓展的运算空间。

图4 除法器系统模块(a) 传统型除法器，(b) 循环型除法器

传统型除法器主要采用递减和比较两种操作，故其空间没有进行拓展。而在循环型除法器除了采用递减和比较外，还增加移位操作，故其操作空间需要进行拓展。从图3可以看出，循环型除法器比传统型除法器多使用了两个48位的操作空间，管脚增加96个，当然在实际使用时并不需要占用寄存器单元，定义Wire类型即可。

本除法器的设计基于美国Altera公司的StratixII系列的EP2S60F1020I4芯片开发。经QuartusII编译综合后，循环性除法器最高工作频率能达到288.94MHz，而传统除法器最高工作频率为188.43MHz。表1为经QuartusII软件编译、综合及时序分析后传统型和循环型除法器芯片资源占用情况比较。从表1可得知，传统型除法器实现组合逻辑和时序逻辑总的逻辑单元数为206个，而循环型除法器需要315个，比传统型除法器增加99个，增加了逻辑资源占用量，同时在管脚数上也多使用96个，说明循环型除法器牺牲部分逻辑单元和管脚提高了除法器的运算速度。

表1 逻辑资源占用

4 仿真结果及分析

在ModelSim仿真工具下对传统型除法器和循环型除法器分别进行仿真，假设Dividend和Divisor分别取4组数据如下：−50/4、127000/−534、52700/850、−16434/−1558。仿真波形如图5所示。

Sq_diff[47:0]和Sq_temp[47:0]分别为在仿真中便于观察的空间和空间。从图5(a)可知，传统除法器在不一样的被除数和除数情况下，就有不一样的时钟消耗，在被除数和除数相差较小时（−50/4和−16434/−1558），所用时钟周期较少；被除数和除数相差较大时（127000/−534和52700/850），所用时钟周期较多，且被除数和除数相差越大，所花时钟周期越多，如127000/−534比52700/850所花时钟周期多。这就说明只要被除数和除数相差较大，传统型除法器就要“多吃”时钟。而循环型除法器完成除法运算具有固定的时钟周期消耗，不会因为被除数和除数而变化，如图5(b)所示。

图5显示，在ModelSim仿真工具中，系统时钟频率设定为50MHz，当被除数和除数相差较小，如被除数为−16434、除数为−1558时，循环型除法器完成一次除法运算只需要0.75ms，而传统型除法器则需要的时间为0.35ms，循环型除法器的运算速度没有体现出来；但是当被除数和除数相差较大，如被除数127000、除数为−534时，循环型除法器完成一次除法运算只需要0.75ms，而传统型除法器则需要4.5ms，循环型除法器比传统型除法器的运算速度提高了6倍。因此针对传统型除法器因被除数与除数相差比较大，而“吃时钟”的现象，循环型除法器很好地克服了这个弊端，提高了除法运算整体的运算速度，同时也对完成每次除法器的运算时钟周期有准确的把握。

5 场平坦度控制及测试

依托循环型触发器算法，设计场平坦度环路控制逻辑，同时在场平坦度控制中，为了减少步进电机驱动马达的频率，采用二级阈值控制，具体如图6所示。黑粗线表示场平坦度的活动范围，±1表示场平坦度控制环路启动马达阈值设置，±2表示场平坦度控制环路马达停止阈值，实线箭头表示场平坦度在此范围内变化过程中马达是动作的，虚线箭头表示场平坦度变化过程时马达是不动作的。场平坦度环路失衡超过一定阈值时，驱动同一腔上的步进电机朝相反方向动作。

图6 场平坦度环路中马达动作关系

图7为采用传统型和循环型除法器监测得到的场平坦度（图7(b)作为控制用，图7(a)作为监测用），从结果来看，数据已经出现错误，不能在工程上使用。具体原因可以通过比较传统型和循环型除法器的算法设计可知，循环型除法器能确定除法运算所需要的时钟周期，运算过程主要采取移位操作，且考虑到同步因素，被除数和除数实际是在另外的寄存器中进行运算；而传统型除法器未考虑以上三点因素，虽然仿真可以通过，但是在实际工程应用中则不能有效地工作。

上海光源增强器主要是对能量为150MeV的电子补充能量，主要工作在升能模式，在长达10h的时间内，采用循环型除法器能使场平坦度的控制稳定在±1.3%以内，优于设计指标(≤±4%)，如图7(b)所示。

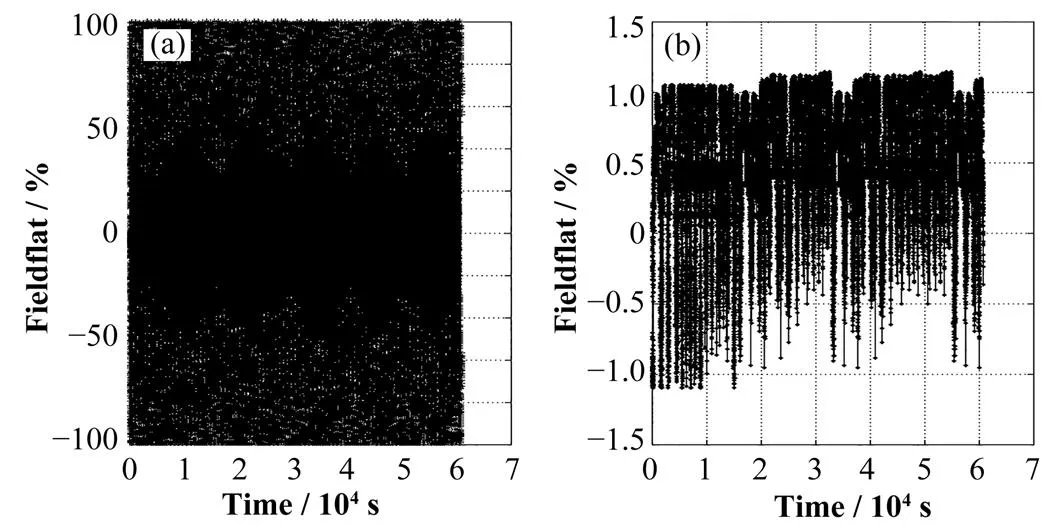
图7 在升能模式下的场平度稳定性(a) 传统型除法器，(b) 循环型除法器

6 结语

除法作为多cell腔的场平坦度控制中最重要的算法，但因传统除法器存在完成一次算法时钟周期不固定且有“吃时钟”的弊端，同时在实际工程中将不能有效地工作，故升级改进为基于Verilog HDL硬件描述语言的循环型除法器。循环型除法器在系统最高工作频率、完成算法时钟数是否固定以及被除数和除数相差较大时所消耗的时钟周期都得到明显提升。在上海光源增强器高频数字低电平控制器中采用循环型除法器，实现了场平坦度稳定度在±1.3%以内，完成每次运算所需35个时钟周期，优于设计指标(≤±4%)。

1 Zhang Z G, Zhao Y B, Xu K,. Digital LLRF controller for SSRF booster RF system upgrade[J]. Nuclear Science and Techniques, 2015, 26(3): 030106. DOI: 10.13538/j.1001-8042/nst.26.030106.

2 Hassanzadegan H, Perez F. Analogue LLRF for the ALBA booster[C]. Proceedings of the 11th European Particle Accelerator Conference, Genoa, Italy, 2008: 1416−1418.

3 Jiang M H, Yang X, Xu H J,. Shanghai synchrotron radiation facility[J]. Chinese Science Bulletin, 2009, 54: 4171–4181. DOI: 10.1007/s11434-009-0689-y.

4 Gu Q, Chen L X, Chen M,. RF system for the SSRF booster synchrotron[C]. Proceedings of the 11th European Particle Accelerator Conference, Genoa, Italy, 2008: 754–756.

5 张志刚, 赵玉彬, 徐凯, 等. 基于I/Q解调原理的校准方法及实验[J]. 核技术, 2015, 38(3): 030102. DOI: 10. 11889/j.0253-3219.2015.hjs.38.030102.

ZHANG Zhigang, ZHAO Yubin, XU Kai,. Calibration method and experiment based on I/Q demodulation principle[J]. Nuclear Techniques, 2015, 38(3): 030102. DOI: 10.11889/j.0253-3219.2015.hjs.38. 030102.

6 钟少鹏, 赵明华, 张俊强. 数字化I/Q技术用于磁控管频率控制[J]. 核技术, 2014, 37(4): 040103. DOI: 10.11889/j.0253-3219.2014.hjs.37.040103.

ZHONG Shaopeng, ZHAO Minghua, ZHANG Junqiang. Digital I/Q technology used for magnetron frequency control[J]. Nuclear Techniques, 2014, 37(4): 040103. DOI: 10.11889/j.0253-3219.2014.hjs.37.040103.

7 刘波. 精通Verilog HDL 语言编程[M]. 北京: 电子工业出版社, 2007: 461‒464. LIU Bo. Proficient in Verilog HDL programming language[M]. Beijing: Electronic Industry Press, 2007: 461‒464.

8 叶显阳, 张海勇, 皮代军, 等. 基于Verilog计算精度可调的整数除法器的设计[J]. 现代电子技术, 2009, 32(3): 146–148. DOI: 10.3969/j.issn.1004-373x.2009.03.046.

YE Xianyang, ZHANG Haiyong, PI Daijun,. Design of integer divider with adjustable precision based on Verilog[J]. Modern Electronics Technique, 2009, 32(3): 146–148. DOI: 10.3969/j.issn.1004-373x.2009.03.046.

9 周殿凤, 王俊华. 基于FPGA的32位除法器设计[J]. 信息化研究, 2010, 36(3): 26–28. DOI: 10.3969/j.issn. 1674-4888.2010.03.008.

ZHOU Dianfeng, WANG Junhua. Design of a 32-bit divider based on FPGA[J]. Informatization Research, 2010, 36(3): 26–28. DOI: 10.3969/j.issn.1674-4888.2010. 03.008.

10 李文彬, 陈金鹰, 王惟洁, 等. 基于FPGA的32位循环型除法器设计[J]. 物联网技术, 2014, 25(11): 62–63. DOI: 10. 3969/j.issn.2095-1302.2014.11.025.

LI Wenbin, CHEN Jinying, WANG Weijie,. Design of a 32-bit circular divider based on FPGA[J]. Internet of Things, 2014, 25(11): 62–63. DOI: 10.3969/j.issn. 2095-1302.2014.11.025.

Control of field flatness based on FPGA for multi-cell cavity

ZHANG Zhigang1,2ZHAO Yubin1,2XU Kai1,2ZHENG Xiang1,2LI Zheng1,2ZHAO Shenjie1,2CHANG Qiang1,2HOU Hongtao1,2LIU Jianfei1,2

1(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China)2(Shanghai Key Laboratory of Cryogenics & Superconducting RF Technology, Shanghai 201800, China)

Background: The most important processing is division in the algorithm for the field flatness controller on multi-cell cavity. The algorithm in conventional integer division uses multiple subtraction and shift methods to achieve the operation. A lot of clocks are consumed in the subtraction process, and the cycles consuming is not fixed on each cycle of the division. Purpose: This study aims to design a circular unrecoverable divider based on FPGA (Field-Programmable Gate Array). Methods: Improvement is taken for meliorating the program structure and optimizing the time sequences to achieve speedup of the division and same clock cycle for each conventional division. This algorithm is implemented on FPGA chip using QuartusII, simulated and verified by ModelSim toolkits. Results: The stability of field flatness is less than ±1.3% and 35 cycles for each algorithm when it applied in the controller of DLLRF (Digital Low Level Radio Frequency) for the booster of Shanghai Synchrotron Radiation Facility (SSRF). Conclusion: Control of field flatness based on FPGA for multi-cell cavity satisfies all functional requirements, overperforms the design expectations.

FPGA, Conventional, Divider, Field flatness control, Clock cycle

ZHANG Zhigang, male, born in 1981, graduated from University of Chinese Academy of Sciences with a doctoral degree in 2015, focusing on the controller on low level radio frequency

LIU Jianfei, E-mail: liujianfei@sinap.ac.cn

2016-09-05, accepted date: 2016-11-18

TL506

10.11889/j.0253-3219.2017.hjs.40.020101

张志刚，男，1981年出生，2015年于中国科学院大学获博士学位，主要从事低电平研究

刘建飞，E-mail: liujianfei@sinap.ac.cn

2016-09-05，

2016-11-18

Supported by National Natural Science Foundation of China (No.11335014)

国家自然科学基金(No.11335014)资助