干湿循环作用下长沙绕城高速公路粉质黏土的损伤特性

李文，曾胜，赵健，刘盼



干湿循环作用下长沙绕城高速公路粉质黏土的损伤特性

李文，曾胜，赵健，刘盼

(长沙理工大学交通运输工程学院，湖南长沙，410006)

为得到干湿循环作用下的长沙绕城高速公路粉质黏土损伤特性，基于连续损伤力学和统计理论，对土体劣化过程进行分析。在假定土体微元强度服从正态分布的基础上将干湿循环损伤变量直接耦合至统计损伤本构模型，从而推导土体在干湿循环作用下的损伤本构方程。结合长沙绕城高速粉质黏土三轴固结不排水实验，着重分析干湿循环次数对土体微元强度的影响。研究结果表明：在干湿循环作用下，长沙绕城高速公路粉质黏土统计损伤本构模型应力−应变计算曲线与实验实测结果相吻合；拟合度均在0.95以上，土体经历1次或2次干湿循环作用后，其微元强度会有一定幅值降低，而后变化幅度较小；土体微元强度离散性受干湿循环作用影响，并随循环次数增多呈增大趋势。

粉质黏土；干湿循环；本构模型；损伤特性

损伤是指材料或结构在外部荷载以及环境的影响下，由于微孔洞、微裂纹等细观结构缺陷引起的劣化过程[1]。宏观损伤理论将存在缺陷的材料体作为一种“连续”且含有“微损伤场”的介质，并将该微损伤的形成、生长、传播和聚结看作是“损伤演变”的过程，它是将“损伤”作为物质细观结构的一部分引入连续介质的模型[2]。天然土体可将其天然缺陷(形成时存在的空洞和孔隙)看作损伤。土体在经历干湿循环作用后，其强度和变形参数随循环次数的增加而降低，由此可见土体在干湿循环作用下其性能逐渐劣化[3]，该劣化过程的本质是土体在干湿循环作用下“缺陷”加剧。通常将该劣化过程看作是连续变化的，可用数学模型对其损伤连续的发展演化进行描述[2, 4−6]。人们对有关非饱和土的强度及变形特性实验研究较多，也建立了一系列的本构模型[7−10]。本文作者在假定非饱和土微元强度服从正态分布的前提下，考虑土体微元强度受干湿循环的影响，将微元强度与损伤变量结合起来研究其损伤特性。

1 基本假设

土体强度具有不均一性(土体孔隙、裂隙、颗粒接触界面均可看作土体的缺陷)，可采用概率统计方法对其强度进行分析[11−12]。为推导非饱和土统计损伤本构模型，首先进行以下假定：1) 非饱和土服从连续介质理论；2) 非饱和土微元强度服从正态分布；3)非饱和土服从均匀性、横观各向同性假定。

鉴于非饱和土从初始缺陷开始损伤到最终破坏是一个相当复杂的过程，为准确描述其破坏条件，假定土的破坏准则[13]为

(2)

为损伤变量的破坏概率。

有效应力是损伤对应变行为产生影响的主要表现形式，将原始材料本构关系中的应力替换为有效应力即可得到损伤材料的本构关系[15−16]，由此非饱和土的统计损伤本构基本关系式可表述为

(4)

式中：0和0为正态分布参数，反映非饱和土的力学性质。

2 模型构建

据文献[15]及广义胡克定律和应力张量的概念可得应力张量第1不变量1和应力张量第2不变量2：

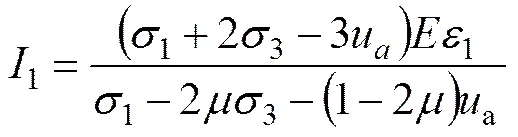
(6)

由式(7)反解得

(8)

根据标准正态分布函数的概念，由式(2)得

鉴于Drucker−Prager破坏准则，确定非饱和土微元强度：

(10)

式中：1为应力张量第一个变量；2为应力张量第二个变量。

将式(5)和(6)代入式(10)可得干湿循环作用下非饱和土微元强度：

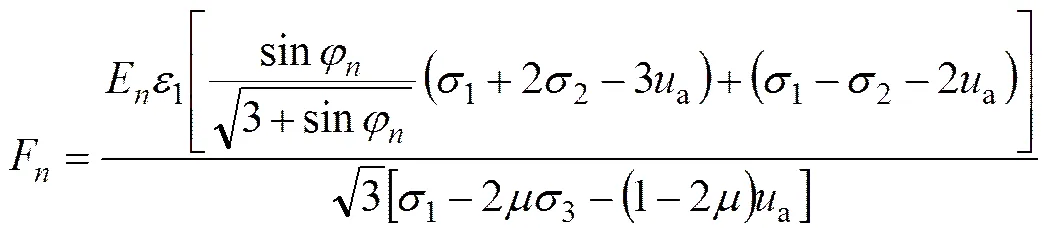
(12)

(13)

式中：1和2为应力张量参数；E为干湿循环次后所对应的弹性模量；0为弹性模量初始值；为干湿循环次后所对应的内摩擦角；为内摩擦角初始值；为干湿循环次数；为模型参数；为模型参数。将干湿循环下非饱和土的微元强度代入式(2)和(3)可得到干湿循环作用下非饱和土损伤演化方程((14))及损伤统计本构关系(式(15))：

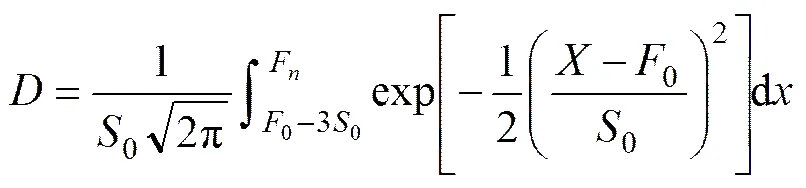
(15)

综上可由应力−应变实验曲线得到干湿循环作用下非饱和土损伤统计本构模型中的，和，同时，在实验过程中可测得a，K，K，，0，和。因此，通过在某条应力−应变曲线上选定一组(和)就能得到对应的次干湿循环作用下的(见式(9))，对应的=(F−0)/0则可通过查标准正态分布函数表得到。利用式(11)计算F，以为横坐标，F为纵坐标，即可得到各条应力应变实验曲线的F−散点图。最后，将问题归结为对式F=求回归系数，即可确定0和0。

3 长沙绕城高速公路粉质黏土损伤特性

为验证前面所述模型的正确性以及研究长沙绕城高速粉质黏土损伤特性，以长沙绕城高速公路粉质黏土为研究对象，根据长沙绕城高速公路路基竣工时间较长且突遇荷载的实际情况，采用固结不排水三轴实验[17]。为了加速固结过程，并使孔隙水压力均匀化，同时也为了便于实验安排、节省时间，在试样四周对称贴上滤纸条，固结时间均为8 h，重度小于0.3 kN/m3，含水量不大于2%。为更好地模拟土体实际应力状态，本次实验考虑进行增大围压实验，先让土体在各向等压应力状态下排水固结，固结完成后保持围压不变，分别在排水条件下和不排水条件下逐渐施加轴向压力，直至试样破坏，围压取100，200，300和400 kPa。

3.1 基于实测数据的模型验证

结合三轴实验系统进行的固结不排水实验结果，将围压为100，200，300和400 kPa下的应力应变关系代入统计损伤本构模型以确定参数，所得结果见图1~4。对得到的散点图进行直线拟合，其表达式可写为

式中：0和0为正态分布参数，反映饱和土力学性质。

拟合参数如表1所示。

按照模型的参数确定方法，得到1，2，3，4，6，8和10次干湿循环作用下的损伤本构参数，并绘制散点图，对散点图进行直线拟合，得到参数0和0如表2所示。

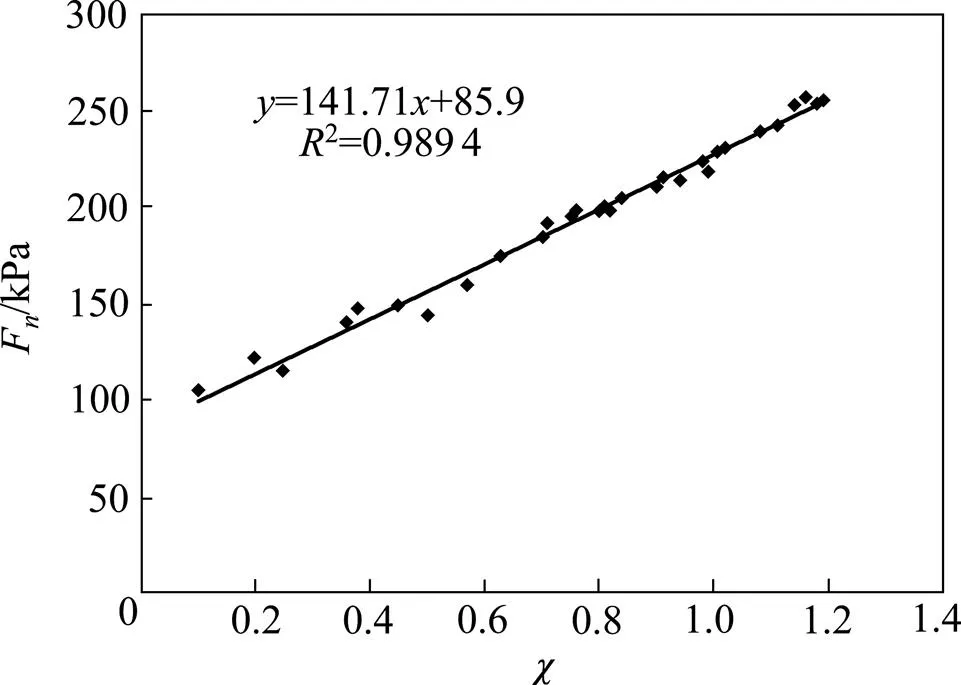
图1 干湿循环次数0次(100 kPa)时的Fn−χ曲线

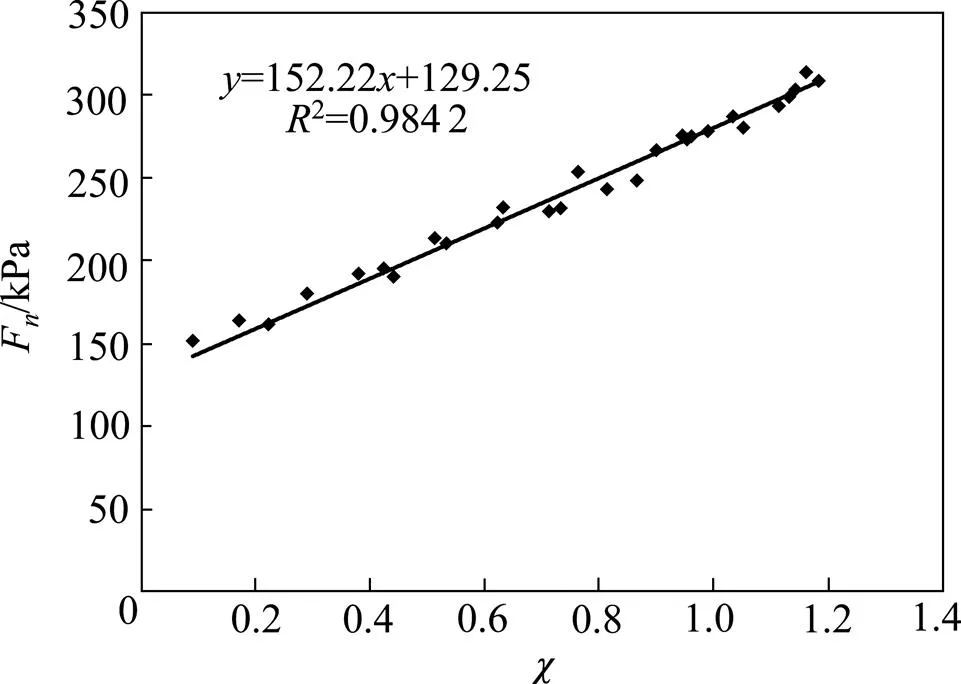
图2 干湿循环次数0次(200 kPa)时的Fn−χ曲线

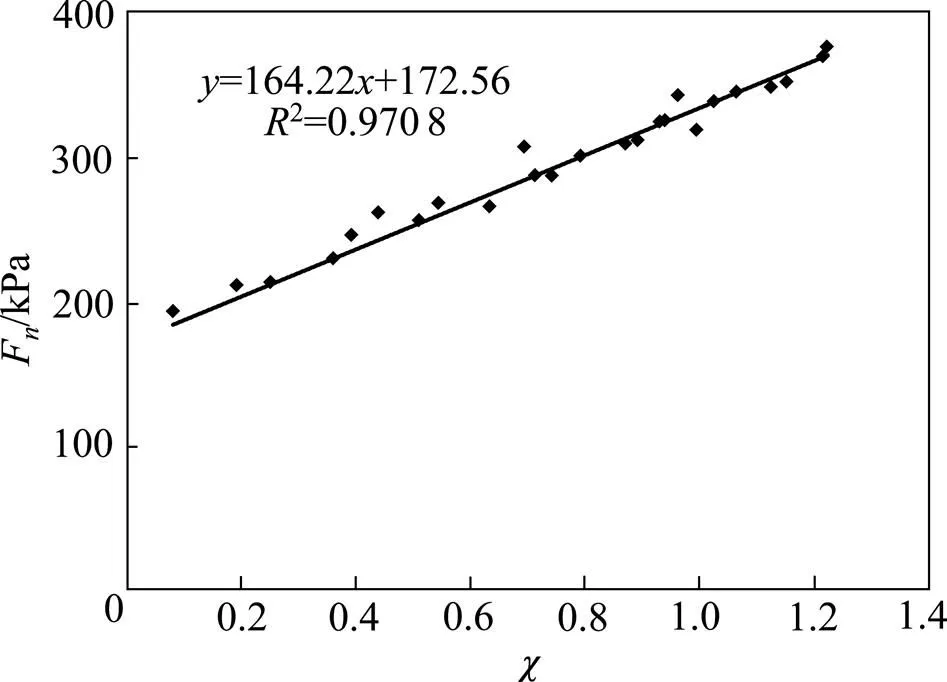
图3 干湿循环次数0次(300 kPa)时的Fn−χ曲线

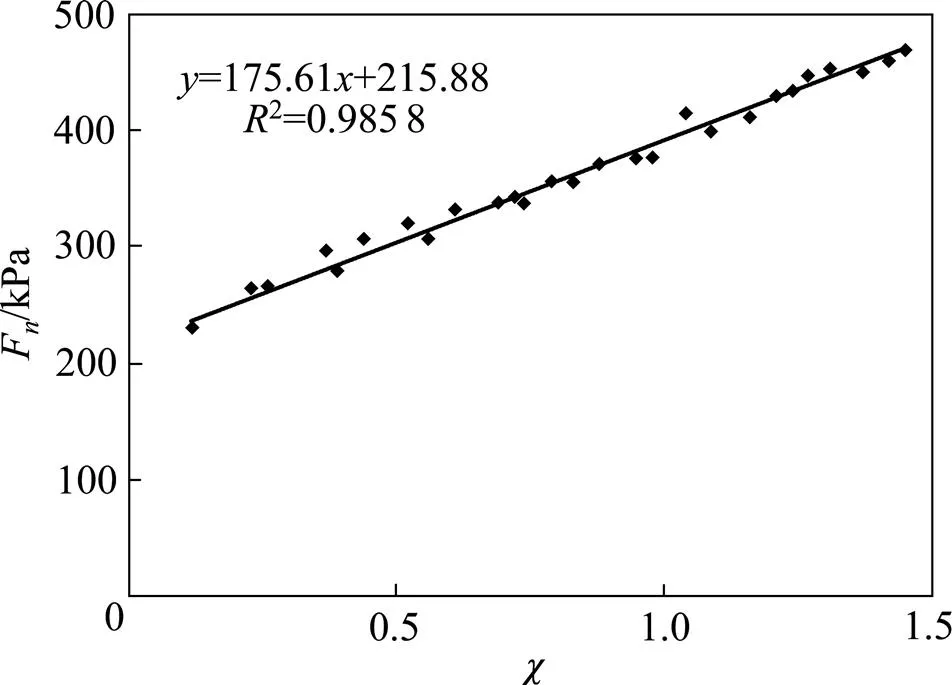
图4 干湿循环次数0次(400 kPa)时的Fn−χ曲线

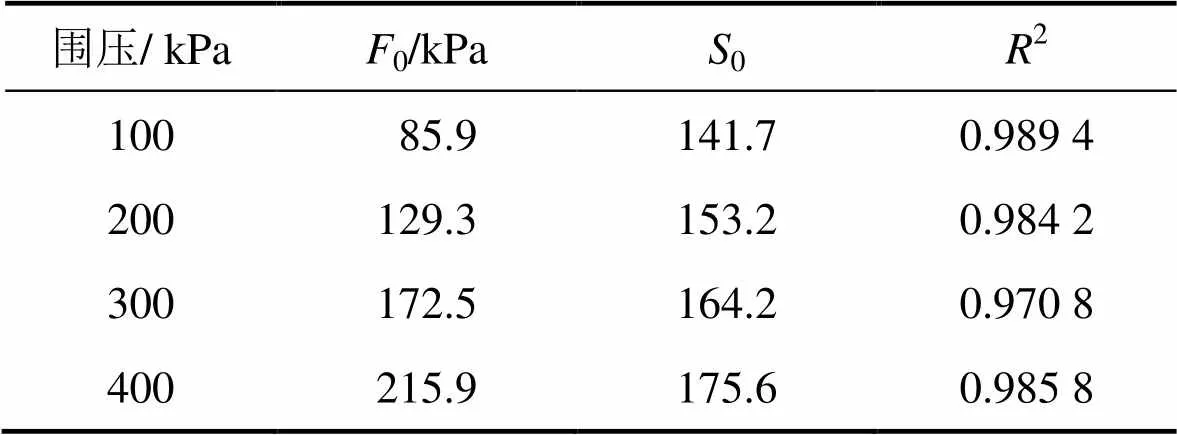
表1 长沙绕城高速粉质黏土不同围压下拟合参数

注：0为非饱和土微元强度均值；0为方差，表示强度离散性，2为拟合度。

从表2可以看出：数据线性关系较好，拟合度均在0.95以上，符合理论推导的微元强度参数线性关系的表达。绘制不同围压下干湿循环次数与模型参数0的关系图，如图5所示。

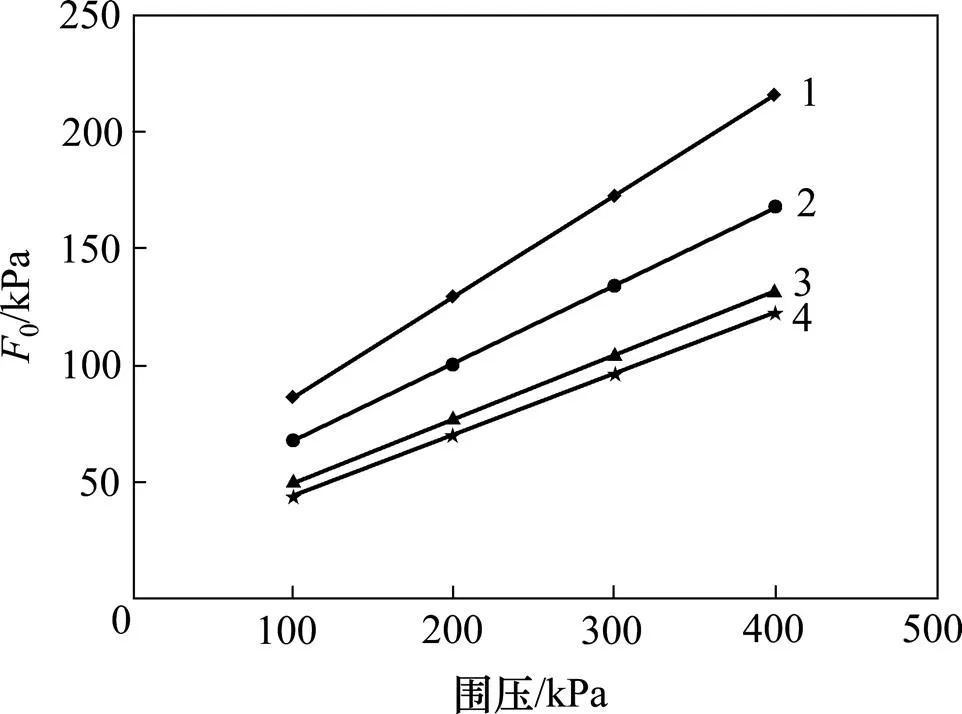
循环数/次：1—0；2—1；3—2；4—10。

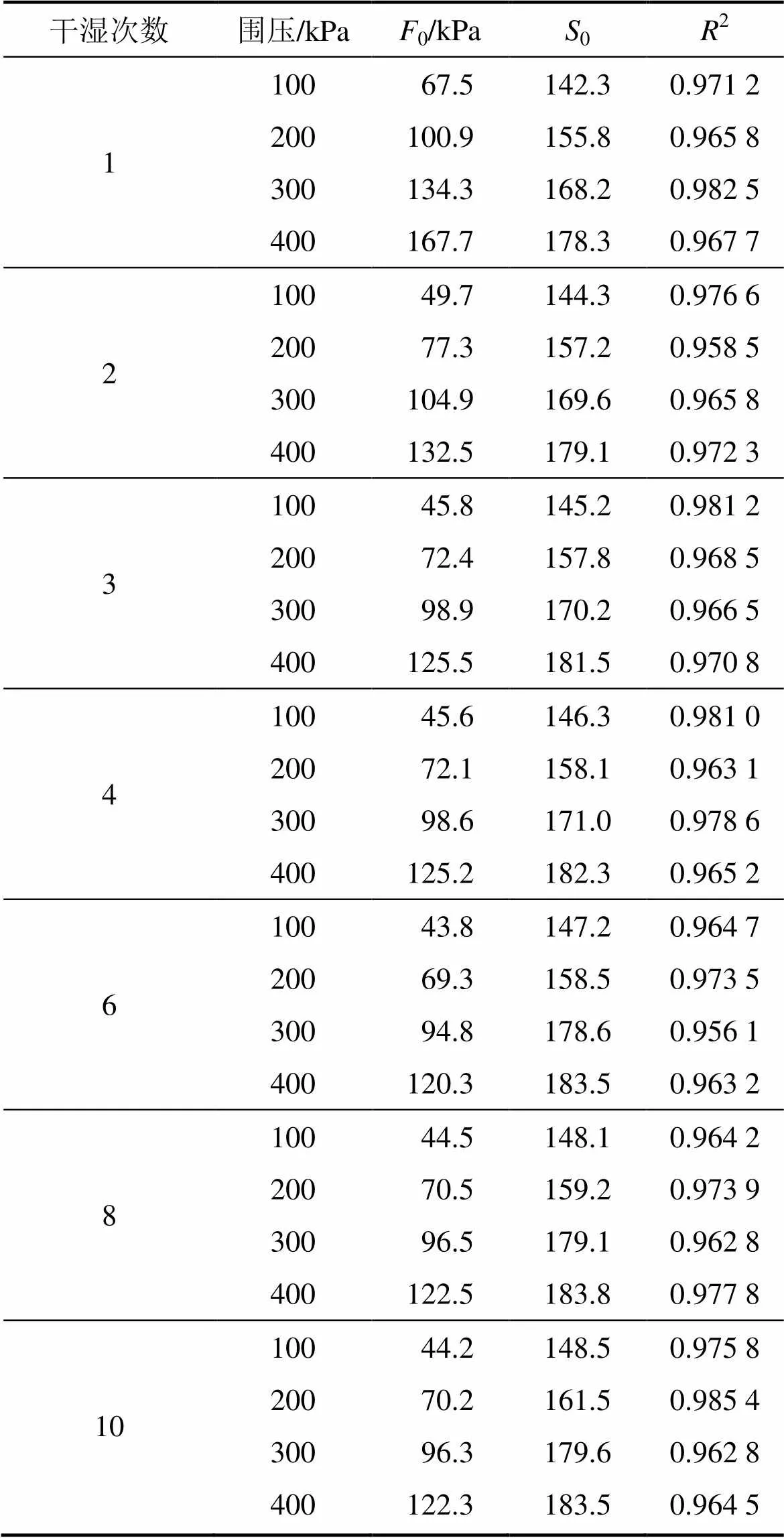
表2 不同干湿循环次数下损伤本构参数拟合结果

注：0为非饱和土微元强度均值；0为方差，表征强度的离散性；2为数据拟合度。

从图5可以看出：微元强度随围压增大而增大，最大值为不经历干湿循环围压为400 kPa时所对应的215.9 kPa，最小值为经历10次干湿循环下围压为 100 kPa时所对应的44.2 kPa，最大值与最小值相差171.7 kPa。由此可以看出，微元强度与围压及干湿循环均有密切联系。围压与微元强度的关系见文献[18−19]，本文就干湿循环次数对微元强度的影响进行分析。

将三轴实验所确定的模型参数代入所述模型，同时将干湿循环作用下非饱和土统计损伤本构模型的计算结果与三轴实验结果进行对比，即可验证模型的正确性。选用围压为200 kPa时的土样应力与应变实验结果对模型进行验证，所得结果见图6。

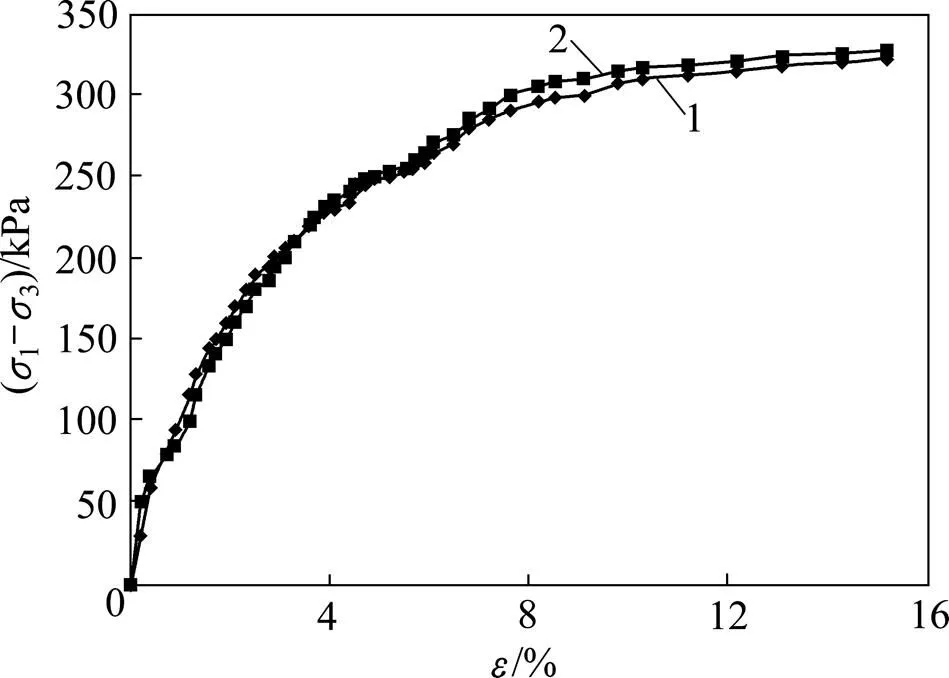
1—模型值；2—实验值。

3.2 干湿循环作用对微元强度均值的影响

基于正态分布的干湿循环作用下非饱和土统计损伤本构模型中参数0的物理意义是表征土体微元强度的平均值，在很大程度上反映了土体的整体强度特性，根据本文所提出的本构模型，计算得到长沙绕城高速粉质黏土第0，1，2，3，4，6，8和10次干湿循环作用下不同围压的0，绘制100 kPa和300 kPa围压下干湿循环作用次数与0的变化曲线，如图7所示。

从图7可以看出：长沙绕城高速粉质黏土微元强度受围压影响较大，具体表现为微元强度随着围压的增大而增大。这是由于适当增强围压使得土体结构更加紧密，土体中存在初始缺陷的部分被愈合，土体微元强度提高。

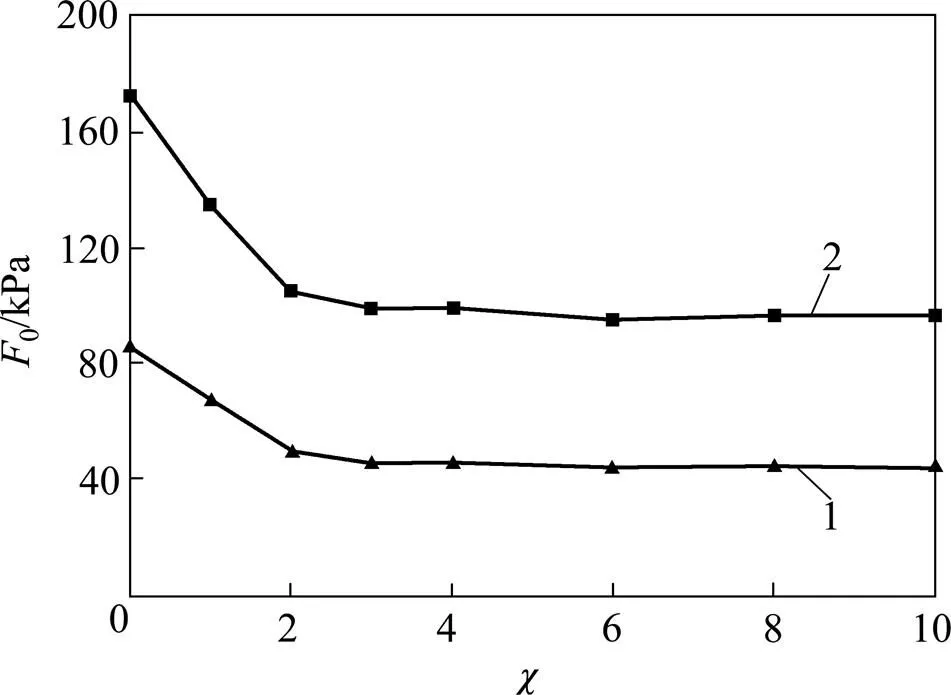
围压/MPa：1—100；2—300。

此外，干湿循环次数对土体微元强度也有一定的影响。从图7可知：土体在经历第1，2，3和4次干湿循环作用后其微元强度变化明显。为进一步分析干湿循环作用次数对微元强度的影响，假定∆为单次循环阶段内的强度劣化值，即

式中：F为第次干湿循环作用下土体微元强度；F−1为第−1次干湿循环作用下土体微元强度。将表2中参数进行处理并绘制100 kPa和300 kPa围压下∆与干湿循环次数关系曲线，如图8所示。

围压/MPa：1—100；2—300。

图8 阶段内变化量∆与干湿循环次数的关系曲线

Fig. 8 Relationship between cycles and ∆

从图8可以看出：微元强度阶段内变化量∆的最大值均在第1和第2次，且明显高于其他循环阶段的劣化值，最大值为42.8 kPa。这表明土体经历1次或2次干湿循环作用后，微元强度会有一定幅值降低，而后变化幅度较小，可视为长期缓慢的变化过程。从土体结构变化角度分析，可认为土体重塑后，在经历1次干湿循环作用，土体一些缺陷结构得到进一步发展直至稳定。

3.3 干湿循环作用对微元强度离散性的影响

基于正态分布的干湿循环作用下非饱和土统计损伤本构模型中参数0的物理意义是表征土体微元强度的离散特性，土体为非均质材料，但在工程实际计算中往往将其视为均质材料，因此，根据本文所提出的本构模型，计算得到长沙绕城高速粉质黏土第0，1，2，3，4，6，8和10次干湿循环作用下不同围压的0，以100 kPa和300 kPa围压下土体微元强度变化情况分析干湿循环作用次数对微元强度离散特性的影响，据其模型计算结果绘制干湿循环作用次数与0的变化关系曲线，如图9所示。

围压/MPa：1—100；2—300。

由图9可以看出：长沙绕城高速粉质黏土微元强度的离散性质受围压影响，具体体现为微元强度随围压增大而增大。这是由于土体在围压作用下部分初始缺陷得到愈合，而部分初始缺陷加剧，故离散程度增大。同时，干湿循环次数也在一定程度上影响微元强度离散性，但其作用变化幅度并不明显。为进一步分析干湿循环作用次数对微元强度离散特性的影响，假定∆为单次循环阶段内离散程度变化值，即

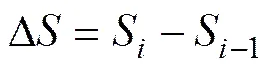
式中：S为第次干湿循环作用下土体微元强度方差；S−1为第−1次干湿循环作用下土体微元强度方差。将表2中数据进行处理分析得出∆与干湿循环次数关系曲线，如图10所示。

由图10可以看出：微元强度阶段内变化量∆均在一稳定值上、下波动，说明干湿循环作用对土体的离散特性影响有一定规律，且阶段内变化量∆变化幅度均在第1和第2次高于其他循环阶段的劣化量。这表明土体经历1次或2次干湿循环作用后，土体结构得到进一步重塑调整并趋于稳定，在此后的干湿循环作用下变化逐渐降低；此外，当围压为300 kPa时，第6次循环作用的土体微元强度离散特性变化较大，可认为在这个干湿循环阶段内土体存在某一缺陷，导致土体离散特性发生巨变，因此，土体微元强度离散性受干湿循环作用影响，并随循环次数增大呈增大趋势。

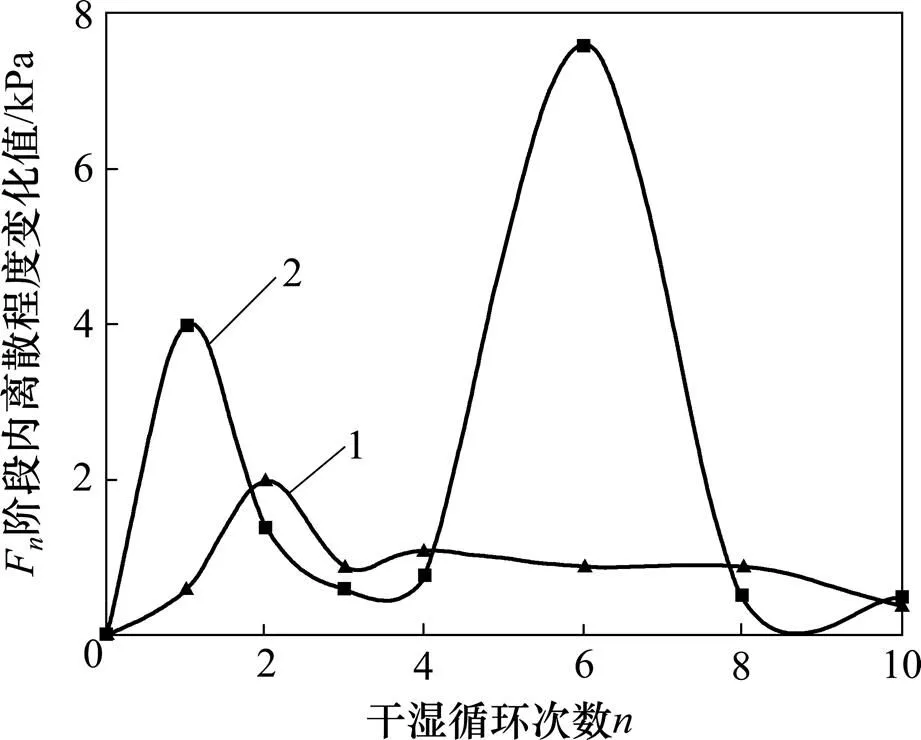
围压/MPa：1—100；2—300。

4 结论

1) 由本文提出的干湿循环作用下长沙绕城高速粉质黏土统计损伤本构模型所得计算结果与实验实测结果相吻合，表明模型的正确性。

2) 土体经历1次或2次干湿循环作用后，微元强度会有一定幅值降低，而后变化幅度较小，可视为长期缓慢的变化过程。

3) 土体微元强度离散性受干湿循环作用影响，并随循环次数增多呈增大趋势。

[1] 商怀帅, 杨鲁生. 基于损伤理论的混凝土双轴压本构模型[J].中南大学学报(自然科学版), 2013, 44(1): 340−344. SHANG Huaishuai, YANG Lusheng. Constitutive model of damage of concrete under biaxial compression[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 340−344.

[2] 傅晏. 干湿循环水岩相互作用下岩石劣化机理研究[D]. 重庆: 重庆大学土木工程学院, 2010: 1−3. FU Yan. Study on water-rock interaction with the cyclic drying-wetting effect on rock[D]. Chongqing: Chongqing University. College of Civil Engineering, 2010: 1−3.

[3] 周雄, 胡海波. 干湿循环作用下高液限黏土抗剪强度实验研究[J]. 公路工程, 2014, 39(5): 352−355. ZHOU Xiong, HU Haibo. Study on shear strength test of high liquid limit clay undue dry-wet cycles[J]. Highway Engineering, 2014, 39(5): 352−355.

[4] 龚壁卫, 周小文, 周武华. 干−湿循环过程中吸力与强度关系研究[J]. 岩土工程学报, 2006, 28(2): 207−209. GONG Biwei, ZHOU Xiaowen, ZHOU Wuhua. Test on suction and strength of expansive soil in a desorption-absorption cycle of moisture[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 207−209.

[5] 慕现杰, 张小平. 干湿循环条件下膨胀土力学性能实验研究[J]. 岩土力学, 2008, 28(S1): 580−582. MU Xianjie, ZHANG Xiaoping. Research on mechanical properties of expansive soil under wetting-drying cycle[J].Rock and Soil Mechanics, 2008, 28(S1): 580−582.

[6] 李向阳, 胡海波, 郭威. 干湿循环条件下路基黏土的强度衰减规律实验研究[J]. 公路工程, 2014, 39(1): 150−152. LI Xiangyang, HU Haibo, GUO Wei. Dry-wet circulation intensity attenuation law of subgrade under the condition of clay[J]. Highway Engineering, 2014, 39(1): 150−152.

[7] 沈珠江. 结构性黏土的非线性损伤力学模型[J]. 水利水运科学研究, 1993(3): 247−255.SHEN Zhujiang. A nonlinear damage model for structured clay[J]. Hydro-Science and Engineering, 1993(3): 247−255.

[8] 李建华, 祝方才, 陈春鸣, 等. 非饱和膨胀土抗剪强度的三轴实验研究[J]. 公路工程, 2011, 36(2): 31−33. LI Jianhua, ZHU Fangcai, CHEN Chunming, et al. Experimental study of triaxial test of unsaturated expansive soil shear strength[J]. Highway Engineering, 2011, 36(2): 31−33.

[9] 刘小平, 袁腾方, 杨迎冬. 湖南非饱和红黏土工程性质的实验研究[J]. 公路工程, 2011, 36(2): 48−52. LIU Xiaoping, YUAN Tengfang, YANG Yingdong. A trial on the properties of the Hunan unsaturated red clay[J]. Highway Engineering, 2011, 36(2): 48−52.

[10] 王朝阳, 许强, 倪万魁, 等. 非饱和原状黄土的非线性损伤本构模型研究[J]. 岩土力学, 2010, 31(4): 1108−1111. WANG Zhaoyang, XU Qiang, NI Wankui, et al. A nonlinear damage constitutive model of unsaturated undisturbed loess[J]. Rock and Soil Mechanics, 2010, 31(4): 1108−1111.

[11] 谢星, 王东红, 赵法锁. 基于Weibull分布的黄土状土的单轴损伤模型[J]. 工程地质学报, 2013, 21(2): 313−317. XIE Xing, WANG Donghong, ZHAO Fasuo. Weibull random distribution based damage constitution model of loessial soils under uniaxial compression[J]. Journal of Engineering Geology, 2013, 21(2): 313−317.

[12] 颜王吉, 黄天立, 任伟新. 基于单元模态应变能灵敏度的结构损伤统计识别[J]. 中南大学学报(自然科学版), 2011, 42(1): 152−157. YAN Wangji, HUANG Tianli, REN Weixin. Statistical damage identification of structures based on element modal strain energy sensitivity[J]. Journal of Central South University (Science and Technology), 2011, 42(1): 152−157.

[13] 孙龙. 非饱和土统计损伤本构模型实验研究及工程应用[D]. 长沙: 湖南大学土木工程学院, 2014: 35−36. SUN Long. Test research and engineering applications of unsaturated soil constitutive model based on statistical damage theory[D]. Changsha: Hunan University. College of Civil Engineering, 2014: 35−36.

[14] 袁腾方. 基于统计损伤理论的沥青路面疲劳失效过程分析[J]. 公路工程, 2010, 35(2): 43−46. YUAN Tengfang. Study on fatigue failure process for asphalt pavement by statistical damage theory[J]. Highway Engineering, 2010, 35(2): 43−46.

[15] 牛军贤. 基于WF三轴系统非饱和土损伤统计本构模型实验研究[D]. 兰州: 兰州理工大学土木工程学院, 2006: 31−33. NIU Junxian. Test research on damage statistic constitutive model of unsaturated soil using WF triaxial apparatus[D]. Lanzhou: Lanzhou University of Technology. School of Civil Engineering, 2006: 31−33.

[16] 赵怡晴, 刘红岩, 吕淑然, 等. 基于宏观和细观缺陷耦合的节理岩体损伤本构模型[J]. 中南大学学报(自然科学版), 2015, 46(4): 1489−1496. ZHAO Yiqing, LIU Hongyan, LÜ Shuran. Damage constitutive model of jointed rock mass based on coupling macroscopic and mesoscopic flaws[J]. Journal of Central South University (Science and Technology), 2015, 46(4): 1489−1496.

[17] 曹文贵, 张升, 赵明华. 饱和土变形过程模拟的统计损伤方法研究[J]. 岩土力学, 2008, 29(1): 13−17. CAO Wengui, ZHANG Sheng, ZHAO Minghua. Study on simulation of deformation process of saturated soils by statistical damage theory[J]. Rock and Soil Mechanics, 2008, 29(1): 13−17.

[18] 韦文婧, 黄良. 浅议常规三轴实验及其参数指标的选用[J]. 广西大学学报(自然科学版), 2006, 31(3): 262−264. WEI Wenjing, HUANG Liang. Definition on conventional triaxial test and selections of its parameter indexes[J]. Journal of Guangxi University (National Science Edition), 2006, 31(3): 262−264.

[19] 杨明辉, 孙龙, 赵明华, 等. 基于统计损伤理论的非饱和土简易本构模型[J]. 水文地质工程地质, 2015(3): 43−48, 58. YANG Minghui, SUN Long, ZHAO Minghua, et al. A simplified unsaturated soil constitutive model based on statistical damage theory[J]. Hydrogeology & Engineering Geology, 2015(3): 43−48, 58.

(编辑 陈灿华)

Damage characteristics of Changsha ring expressway silty clay during dry-wet cycle

LI Wen, ZENG Sheng, ZHAO Jian, LIU Pan

(School of Traffic and Transportation Engineering, Changsha University of Science and Technology, Changsha 410006, China)

In order to obtain silty clay’s damage characteristics of Changsha ring expressway during dry-wet cycle, soil degradation processes were analyzed based on the continuous damage mechanics and statistical theories. Assuming soil micro strength was normally distributed, dry-wet cycle damage variable was directly coupled to the statistical damage constitutive model. Then, the damage constitutive equation of soil was built under the effect of dry-wet cycle. Meanwhile, combing with the triaxial consolidated undrained test about Changsha ring expressway silty clay, the impact of dry-wet cycle on soil infinitesimal strength was analyzed. The results show that calculation results of statistical damage constitutive model about Changsha ring expressway silty clay during dry-wet cycle are accordance with the experimental results, and the degree of fitting is above 0.95. After one or two dry-wet cycle interactions, soil’s infinitesimal strength will reduce to some extent, and then there will be small changes in amplitude. The discreteness of soil’s infinitesimal strength is influenced by dry-wet cycle and tends to increase with cycles times.

silty clay; dry-wet cycle; constitutive model; damage characteristics

10.11817/j.issn.1672-7207.2017.05.031

TU442

A

1672−7207(2017)05−1360−07

2016−06−10；

2016−08−22

交通运输部建设科技项目(2011318824350)；国家自然科学基金资助项目(50208004) (Project(2011318824350) supported by the Construction of Science and Technology of Ministry of Transport; Project(51374248) supported by the National Natural Science Foundation of China)

李文，博士研究生，从事路基路面工程及边坡工程等研究；E-mail: 617303487@qq.com