基于空间计量的碳排放量影响因素分析

付云鹏，马树才



基于空间计量的碳排放量影响因素分析

付云鹏，马树才

(辽宁大学经济学院，辽宁沈阳，110036)

在对2000−2014年中国30个地区的碳排放量进行估算的基础上，利用Moran’s I检验法对区域碳排放量进行了空间相关性检验。在此基础上以扩展的STIRPAT模型为理论基础，借助空间回归模型研究了人口结构、产业结构、能源结构、技术水平等因素对碳排放量的影响效应。结果显示：产业结构、人口规模和技术水平是碳排放量的主要影响因素，产业结构和人口规模对碳排放量的影响是正向的，技术水平对碳排放量的影响是负向的。

人口规模；产业结构；技术水平；空间自相关；空间回归模型

一、引言及相关文献综述

人口与资源环境的关系非常密切、复杂，人口规模、结构、质量等因素都与资源环境密切相关，因此，不少学者开始关注人口与碳排放之间的关系问题，而随着空间计量经济学的发展，也使得对碳排放问题的研究考虑了空间因素的影响。中国是一个地广人多的国家，经济发展、产业结构、人口分布、消费结构等都存在着一定的地域差异。因此在研究碳排放量的影响因素时考虑空间因素的影响有着非常重要的理论和现实意义。Ehrlich和Holdren[1]为定量地研究人口对环境的影响提出了著名的IPAT方程。Dietz和Rose等[2]将IPAT方程改写成随机形式并称之为STIRPAT模型，该模型克服了IPAT方程中解释变量同比例变动的不足，是一个含有多个解释变量的指数形式的模型，模型系数可以理解为环境变量对各影响因素的弹性，STIRPAT模型在应用过程中比较灵活，同时还可以根据研究需要加入其他影响环境变量的解释变量。该模型为研究人口因素、社会财富和技术水平等因素对环境变量的影响提供了新的依据，为研究人口与环境间的关系奠定了新的理论基础。Mackellar等[3]将IPAT中的“P”用家庭户规模(households)代替，将IPAT改写为IHAT模型，并用这两种模型分析了人口因素对全国能源消费量的影响。York等[4]利用STIRPAT模型研究了人口、经济生产、城市化和地理因素对环境的影响，并解释了跨国排放对环境的影响。肖宏伟等[5]基于扩展 STIRPAT模型和空间杜宾模型研究了人口、产业结构、能源价格等因素对碳排放量和碳排放强度的影响。宋德勇和刘习平[6]基于1978－2010年中国各地区碳排放数据，对碳基尼系数和碳洛伦兹曲线进行了重新定义，并对中国各地区2020年的碳排放量进行了空间分配。Wang Can等[7]利用中国1957－2000年的碳排放数据，采用LMDI方法研究了碳排放量的影响因素，结果显示能源强度、燃料转换和可再生能源的利用是减少碳排放量的积极因素。Wu等[8]利用LMDI分解方法将碳排放强度的影响因素分解为产业结构、能源强度、能源结构和发射系数四种。Ren等[9]利用Divisia指数法探讨了制造业碳排放量的影响因素。范丹[10]利用扩展Johan 恒等式对中国能源消费人均碳排放的影响因素进行了分析，利用LMDI分解法对产业能源消耗碳排放进行分解，根据公式测算出1995－2010年我国能源结构、潜在能源强度、能源绩效、能源技术进步等因素对碳排放的影响效应。许海平[11]采用2000－2008年我国29个省域的空间样本数据研究了城市化水平、贸易开放、非农化就业人员的比重和技术进步对碳排放量的空间影响。Stern D. I. 和Common M. S.[12]应用73个国家1960－1990年的样本数据借助环境EKC研究了人均SO2排放量与人均财富的关系，研究结果表明：减排与时间有关系而不是与收入有关系。Marzio Galeottia和Alessandro Lanzab[13]利用1960−1995年108个国家的CO2作为环境污染的代理变量，研究了人均CO2与人均GDP之间的关系，证明了环境EKC的“倒U”型关系存在。Amy K. Richmond和Robert K. Kaufmann[14]研究了收入和能源使用、收入和碳排放之间的关系，结果显示：对于OECD国家，收入与人均能源使用或者碳排放之间的拐点存在；对于非OECD国家，收入与人均能源使用或者碳排放之间的拐点不存在。Song T等[15]利用中国1985－2005年的省级面板数据，基于环境库兹涅茨曲线假说，以废气、废水、固体废物作为环境指标，以GDP作为经济指标，对废气、废水、固体废物与GDP之间的关系进行了实证分析。数据的协整检验显示：废气、废水、固体废物的人均排放与人均GDP之间均存在着长期的协整关系，三种污染物与GDP之间均呈“倒U”型关系。王建军和周晓唯[16]以空间计量模型为基础研究了人口、能源消费和碳排放量对我国经济的空间溢出效应和空间关联性。杜慧滨等[17]利用Moran 指数和空间面板数据模型研究了1997－2009年我国29个地区碳排放绩效的空间分布特征与影响因素，结果表明：我国区域碳排放绩效存在着较强的区域集群现象。陈德湖和张津[18]利用2000－2009年中国30个省的数据，采用空间面板计量经济模型研究了经济增长与碳排放之间的关系，结果表明：经济发展与碳排放之间存在着显著的空间效应。本文将在前人研究成果的基础上，利用Moran’s I检验法检验中国区域碳排放量的空间相关性，在空间相关性检验的基础上将空间因素考虑到碳排放量影响因素模型的构建中，研究人口规模、人口年龄结构、城市化率、经济产出、产业结构、技术水平和能源消费结构等因素对中国区域碳排放量的影响效应。

二、碳排放量的STIRPAT模型的构建

(一)变量选取及数据来源

目前大多数国内外学者对碳排放问题的研究已由理论分析转向实证分析，主要是利用IPAT方程[19−20]及其扩展模型STIRPAT[21−23]、LMDI[24−25]分解法，分析碳排放量的影响因素及影响效应。碳排放量的影响因素包括经济规模、人口规模、产业结构、能源结构和能源效率等。在借鉴相关研究成果的基础上，选取2000－2014年中国30个地区的省际样本数据，由于西藏地区大量能源消费数据缺失，因此不包含西藏地区。选取人均 GDP、人口规模(年末人口总数)、人口年龄结构(劳动年龄人口占总人口的比重)、产业结构(第二产业增加值占地区生产总值的比重)、城市化率(城镇人口占总人口的比重)、技术水平(专利申请授权数)和能源消费结构(煤炭消费占能源消费总量的比重)7个指标作为碳排放量的影响因素来研究各因素对碳排放量的影响效应。研究过程中考虑空间因素对碳排放量的影响，通过构建空间回归模型进行实证分析。人均GDP、产业结构、人口年龄结构、城镇化率、技术水平数据来源于《中国统计年鉴》历年数据，能源消费结构数据由《中国能源统计年鉴》历年数据经简单计算获得，由于碳排放量没有统计数据，在借鉴李丹丹等[26]、程叶青等[27]研究成果的基础上，利用焦炭、煤炭、煤油、柴油、汽油、原油、燃料油和天然气8类能源的消费量来对碳排放量进行估算，公式如下：

式中：2表示碳排放量，单位为万吨；C表示各类能源的碳排放系数；E表示第种能源的标准煤消费量。《中国能源统计年鉴》中提供的是各类能源消费的实物消费量，在利用公式(1)进行碳排放量的估算之前需将实物消费量都转换为标准煤消费量，各类能源的碳排放系数和标准煤折算系数数据具体见表1。

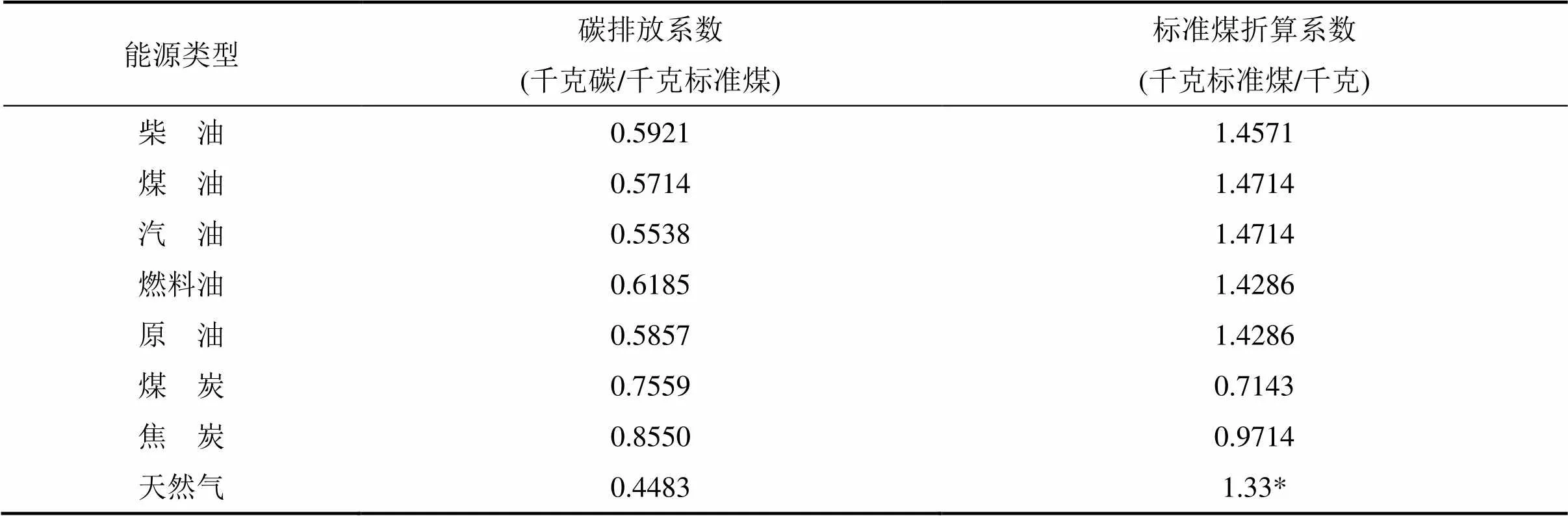
表1 能源的碳排放系数和标准煤折算系数表

注：标准煤折算系数来源于《中国能源统计年鉴2013》，碳排放系数来源于IPCC碳排放计算指南；*表示天然气的标准煤折算系数单位为千克标准煤/立方米

(二)模型构建

IPAT 方程是用来研究人类活动对环境压力的影响的模型，目前该模型已被广泛地应用于研究环境问题，Dietz 和Rosa[2]将 IPAT方程表示成随机形式，即 STIRPAT模型：

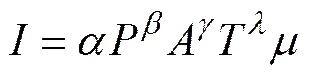
式中：表示环境变量；表示人口规模；表示人均财富；表示技术水平；表示随机误差；表示模型系数；，，表示各因素的参数。将模型(2)两边同时取对数，得到如下线性模型：

ln=ln+ln+ln+ln+ln(3)

在人口对环境的影响中，人口规模是最主要的影响因素。首先，人口作为生产者通过生产活动对环境产生影响，人口规模越大，在就业率不变的情况下，就业人口越多，从而将会有更多的生产者从事生产活动，生产规模的扩大，势必带动更多的能源消费、更多的碳排放和更多的其他环境污染物的排放；其次，人口同时也是消费者，人口消费的各种物质生活资料在生产过程中产生间接的碳排放量。用年末人口数()代表人口规模。

除人口规模外，与碳排放量密切相关的人口因素还包括人口结构，其中最主要的是人口年龄结构和人口城乡结构。近年来中国的老龄化现象凸显，人口年龄结构通过就业、储蓄率、消费结构等对碳排放量产生影响，劳动年龄人口比重越大，从事生产活动的人口越多，从而带来更多的碳排放量，同时，年轻人的消费理念和消费方式与老年人不同，年轻人更倾向于汽车等高排放的生活消费品的消费，因此，人口年龄结构对碳排放量也存在影响。用劳动年龄人口占总人口的比重代表人口年龄结构；人口城乡结构()对碳排放量的影响体现在城乡生活方式的不同；用城市化率()代表人口城乡结构。

人均财富对碳排放量的影响不言而喻，经济产出越多，人均财富越多。但产出多的同时，能源消费越多，从而能源消费带来的碳排放量越多，用人均地区生产总值代表人均财富()。

第二产业相对于农业和第三产业需要更多的能源消费，因此第二产业比重越大，碳排放量越大；用第二产业增加值占地区生产总值的比重代表产业结构()。

技术水平对碳排放量的影响主要通过提高能源利用效率、改变生产方式等途径来实现，减少碳排放量的主要手段只能依赖技术进步。目前大部分学者采用研发投入和专利数量作为技术水平的代理变量，本文采用专利申请授权数代表技术水平()。

能源产品中煤炭类能源的碳排放系数最大，因此煤炭类能源消费比重越大，碳排放总量越大。本文用能源消费总量中煤炭类能源的比重代表能源消费结构()。

根据上述分析，以STIRPAT模型为理论基础，以区域碳排放量(2)作为环境变量，以人口规模()、人口年龄结构()、城市化率()作为影响环境的人口因素，以人均GDP()表示人均财富，同时考虑产业结构()、技术水平()和能源消费结构()对碳排放量的影响，构建如下模型：

ln2i=0+1lnpop+2lnpp+3lncpp+4lngdp+

5lnind+6lnpa+7lnes+(4)

式中：表示中国30个不同的地区。

三、区域碳排放量的空间回归分析

(一)空间相关性检验

1. 全局空间相关性检验

全局空间相关性用以分析空间数据在整个系统内所表现出的分布特征，目前国内外学者大多 采用Moran’s I来度量变量的全局空间相关性，全局Moran’s I的定义为：

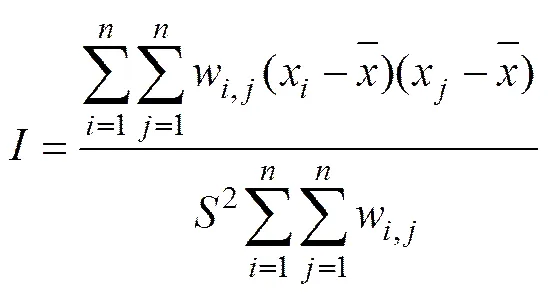
利用空间分析软件GeoDa对中国30个地区2000－2014年的区域碳排放量数据进行空间自相关分析，历年全局空间自相关的Moran’s I值见表2。

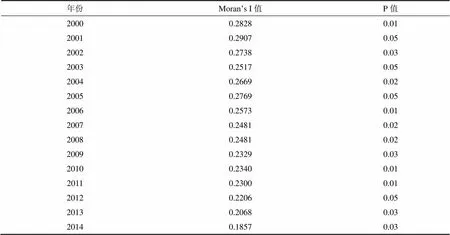
表2 2000－2014年中国区域碳排放量的Moran’s I值

从表2中可以看出2000－2014年中国区域碳排放量间存在明显的空间自相关性，空间相关性指数Moran’s I值总体上呈现先下降，后上升，再下降的趋势。Moran’s I值最大的是2001年，为0.2907，此后Moran’s I值呈下降趋势，下降至2003年的0.2517，2004年又开始上升，2006年之后呈现逐渐下降的趋势。这说明各地区碳排放量的空间集聚程度有所减弱，中国区域碳排量的总体空间差异有所扩大，但仍然呈现比较明显的空间自相关性。

2. 局部空间相关性检验

全局空间自相关指数 Moran’s I揭示了碳排放量的整体空间依赖程度，尚未指出哪些局部地区出现了高值或低值的空间聚集情况。为进一步检验不同年份各地区碳排放量是否具有高值或低值在空间上的集聚现象，还需要进行局部空间自相关检验。局部Moran’sI(或称LISA)是检验局部地区之间是否存在相似或相异的观察值聚集情况的一种指数。局部Moran’s I的定义为：

若I大于0，表示特征值相似的地区是集聚的(“高-高”或“低-低”)；若I小于0，表示特征值不相似的地区是集聚的(“高-低”或“低-高”)。根据不同地区的时空分布特点，选取了具有代表性的年份(2001、2003和2012年) 用GeoDa软件进行分析，可以得到这3年中国区域碳排放量的Moran’s I散点图，如图1所示。

图1 2001、2003和2012年中国区域碳排放量散点图

图1中，2001年的散点图中辽宁省、山西省、山东省、河北省、江苏省、浙江省、黑龙江省、内蒙古自治区、河南省、上海市和安徽省共有11个区域位于散点图的第一象限，碳排放量高的地区与碳排放量高的地区聚集在一起，呈现“高-高”的正向空间相关关系；吉林省、陕西省、福建省、宁夏回族自治区、北京市和天津市共有6个区域位于第二象限，碳排放量低的地区被周围碳排放量高的地区包围，呈现“低-高”聚集的空间关系；江西省、湖南省、广西壮族自治区、海南省、重庆市、四川省、贵州省、云南省、甘肃省、青海省和新疆维吾尔自治区共有11个区域位于第三象限，碳排放量低的地区聚集在一起，呈现“低-低”聚集的空间关系；湖北省和广东省共有2个区域位于第四象限，碳排放量高的地区被周围碳排放量低的地区包围，呈现“高-低”聚集的空间关系。2001年的Moran’s I散点图中“高-高”和“低-低”聚集的类型居于主导地位。2003年的散点图中，辽宁省、山西省、山东省、河北省、江苏省、浙江省、黑龙江省、内蒙古自治区、河南省和上海市共10个区域依旧位于第一象限；吉林省、陕西省、福建省、宁夏回族自治区、北京市和天津市共有6个区域依旧位于第二象限；江西省、湖南省、广西壮族自治区、海南省、重庆市、贵州省、云南省、甘肃省、青海省和新疆维吾尔自治区共有10个区域位于第三象限；四川省、湖北省和广东省共有3个区域位于第四象限。从2001年到2003年各地区的空间聚集现象差别不大，只有安徽省和四川省2个地区发生了变化。2012年的散点图中，山西省、山东省、河北省、江苏省、浙江省、内蒙古自治区、河南省和上海市共8个区域位于第一象限；吉林省、上海市、北京市、天津市、安徽省、黑龙江省和宁夏回族自治区共7个区域位于第二象限；福建省、江西省、湖南省、广西壮族自治区、海南省、重庆市、四川省、贵州省、云南省、甘肃省、青海省和新疆维吾尔自治区共有12个区域位于第三象限；辽宁省和广东省位于第四象限。上述3个时点的Moran’s I散点图总体上呈现出东部和西部地区表现出相似的空间关联性(“高-高”或“低-低”)，而中部地区则表现出非相似的空间关联性(“低-高”或“高-低”)，这说明中国区域碳排放量的空间依赖性和差异性是并存的，但以空间依赖性为主。

(二)区域碳排放量的空间回归分析

由于中国区域碳排放量间空间相关性的存在，使得线性回归模型中空间均质的假设遭到破坏，因此有必要构建空间回归模型对中国区域碳排放量的影响因素及影响程度进行分析，在模型(4)的基础上考虑空间因素对区域碳排放量的影响，构建空间回归模型。常见的空间回归模型有空间误差模型(SEM)和空间滞后模型(SLM)两种。

1. 空间误差模型(Spatial Error Model，SEM)

空间误差模型用不同地区间的空间协方差反映随机误差过程，考虑空间因素的碳排放量的SEM为：

ln2i=0+1lnpop+2lnpp+3lncpp+4lngdp+

5lnind+6lnpa+7lnes++(7)

式中：0为待估计常数项；参数(=1, 2, …, 7)为各解释变量对碳排放量的影响系数；参数为回归残差之间的空间相关性强度，用来衡量样本观测值中的空间依赖作用；为回归残差；是正态分布的随机误差。

2. 空间滞后模型(Spatial Lag Model, SLM)

空间滞后模型考虑的是某一空间对象的因变量不仅与该对象的自变量有关，同时也与相邻对象的因变量有关。考虑空间因素的碳排放量的SLM为：

ln2i=ln2i+0+1lnpop+2lnpp+

3lncpp+4lngdp+5lnind+6lnpa+

7lnes+(8)

式中：为滞后变量系数，用来反映相邻的空间对象之间的空间溢出效应；0为待估计常数项；(=1, 2, …, 7)为各解释变量对碳排放量的影响系数；w,j为空间权重，反映了空间距离对区域行为的作用；为随机误差。

3. 空间回归模型的适用性检验

在利用空间回归模型进行分析前，需要对模型的适用性进行检验。空间回归模型的适用性检验标准为：若空间滞后模型的拉格朗日统计量LM-lag比空间误差模型的拉格朗日统计量LM-error显著，则采用空间滞后模型进行回归分析；反之，则采用空间误差模型进行回归分析。

4. 空间回归分析

空间滞后模型和空间误差模型都是用于分析截面数据的模型，但是单纯应用截面数据进行分析容易忽略变量之间的滞后效应和忽略某些数据信息，因此借鉴吕健等[28]学者的观点采用2000－2014年数据均值进行空间回归分析。将样本数据带入模型(4)，用GeoDa软件先对模型进行普通最小二乘估计(OLS)，估计结果见表3。

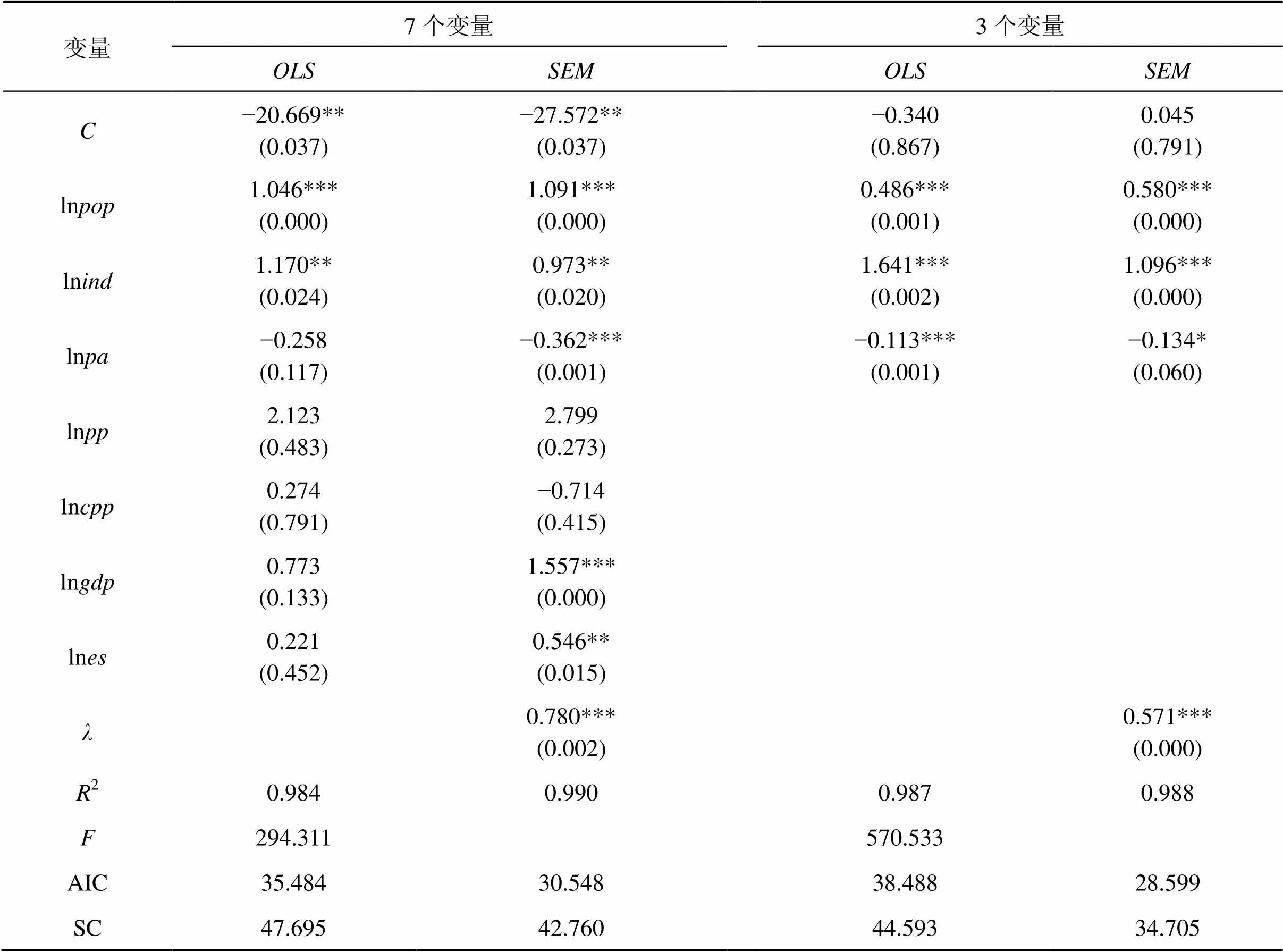
表3 中国区域碳排放量的OLS和SEM估计结果表

变量7个变量3个变量 OLSSEMOLSSEM C−20.669**(0.037)−27.572**(0.037)−0.340(0.867)0.045(0.791) lnpop1.046***(0.000)1.091***(0.000)0.486***(0.001)0.580***(0.000) lnind1.170**(0.024)0.973**(0.020)1.641***(0.002)1.096***(0.000) lnpa−0.258(0.117)−0.362***(0.001)−0.113***(0.001)−0.134*(0.060) lnpp2.123(0.483)2.799(0.273) lncpp0.274(0.791)−0.714(0.415) lngdp0.773(0.133)1.557***(0.000) lnes0.221(0.452)0.546**(0.015) λ0.780***(0.002)0.571***(0.000) R20.9840.9900.9870.988 F294.311570.533 AIC35.48430.54838.48828.599 SC47.69542.76044.59334.705

注：系数下面的括号里为变量显著性检验的P值，***、**和*分别表示1% 、5%和10%的显著性水平

表3中可以看出，普通最小二乘估计的模型2为0.984，模型的拟合优度很好。模型的F统计量为294.311，在1%的显著水平下通过模型的线性关系检验。解释变量的显著性t检验显示：变量ln通过1%显著性水平的变量显著性检验，变量ln通过5%显著性水平的变量显著性检验，变量ln通过10%显著性水平的显著性检验，变量ln、ln、ln和ln没有通过检验，说明这4个变量对被解释变量的解释能力不显著，可能存在多重共线性。进一步进行多重共线性检验发现：ln的方差膨胀因子为14.672，ln的方差膨胀因子为14.672，ln的方差膨胀因子为11.239，都大于临界值10，自变量间存在较高的多重共线性，不能同时作为ln2的解释变量进入模型。采用逐步回归的方法来消除解释变量间的多重共线性，得到只含有ln、ln和ln这3个变量的模型。模型的OLS估计结果见表3。含有3个变量的模型的共线性检验显示：3个变量均通过了多重共线性检验，并且3个变量均通过了5%的变量显著性检验，同时模型的统计量和2也都优于包含7个解释变量的模型，说明含有3个解释变量的模型更加适用于分析碳排放量的影响因素。

模型的适用性检验结果表明：空间误差模型的拉格朗日统计量LM-error比空间滞后模型的拉格朗日统计量LM-lag更加显著，应采用空间误差模型进行空间回归分析，将样本数据带入模型(7)，用GeoDa软件进行分析，得到表3中的空间误差模型的估计结果，为了便于比较同时给出了含有7个变量的空间误差模型的估计结果，但分析过程以含有3个变量的模型为主。

从表3中空间误差模型的回归分析结果可以看出，人口规模、产业结构和技术水平是影响中国区域碳排放量的主要因素。人口规模和产业结构对碳排放量的影响都是正的，说明人口规模和第二产业比重的增加都将带来碳排放量的增加，产业结构的影响系数为1.096，大于人口规模的影响系数0.580，说明产业结构对碳排放量的影响要大于人口规模对碳排放量的影响。技术水平对碳排放量的影响是负的，说明技术水平的提高将带来碳排放量的减少，技术水平对碳排放量的影响系数为−0.134，说明技术水平每提高1%，碳排放量将下降0.134%。此外，碳排放量空间误差模型的空间相关程度系数为0.571，并且通过1%显著性检验，说明碳排放量的空间溢出效应为正，邻近地区的碳排放量对本地区的碳排放量存在正向的空间溢出效应，本地区的碳排放量除了受到本地区人口、经济、产业结构、技术水平等影响外，还受到邻近地区空间溢出效应的影响，邻近地区的碳排放量增加1%，将会对本地区的碳排放量带来0.571%的空间溢出效应。这是传统线性模型无法反映的。

四、结论与建议

在对2000−2014年中国区域碳排放量进行估算的基础上，采用Moran’s I检验法对区域碳排放量的空间相关性进行了检验，在此基础上利用空间误差模型研究了碳排放量的空间依赖性以及人口规模、人均GDP、城市化率、人口年龄结构、产业结构、技术水平、能源消费结构等因素对碳排放量的影响效应，得到以下结论，并提出相应的对策建议。

1. 中国30个地区2000−2014年的碳排放量间存在着明显的空间自相关性

全局空间自相关的Moran’s I值最大的是2001年，此后空间自相关的Moran’s I值总体上呈现下降趋势。东部地区碳排放量“高-高”聚集的现象比较明显，碳排放量高的地区其邻近省份的碳排放量也较高。西部地区碳排放量“低-低”聚集的现象比较明显。

在碳排放量的Moran’s I散点图中，对于位于第一象限呈现“高-高”聚集现象的区域，这些地区自身的碳排放量较高，同时周围地区对其存在空间溢出效应，因此在减排政策制定的时候应先从这些地区入手，将这些地区视为减排的重点区域；对于位于第二象限呈现“低-高”聚集现象的区域，这些地区中心区域碳排放量较低，邻近地区碳排放量较高，在减排政策制定的时候应采取保守的减排态度，由于空间溢出效应的存在邻近地区的碳排放可能会对中心地区造成负面的影响，因此这些地区在制定减排政策的时候应密切关注周围地区的减排政策的制定和实施情况；对于位于第三象限呈现“低-低”聚集现象的区域，碳排放量较低的地区聚集在一起，可以视为减排的缓冲区，这些地区碳排放量相对较低，减排潜力弱，这些地区自身和邻近地区碳排放量都比较低，高排放地区可以借鉴这些地区的减排经验，实现减排的目标；对于位于第四象限呈现“高-低”聚集现象的区域，可视为重点的减排区域，减排潜力大，应制定积极的减排政策，以结构调整促进节能减排，对高能耗行业的新建和扩建进行适度的限制和置换，发展清洁能源和再生能源，同时大力推广和发展节能环保行业。

2. 产业结构是最重要的影响因素

第二产业比重的增加将大幅促进碳排放量的增加，其影响系数为1.096，可见产业结构和碳排放量之间几乎是同比例增长的。第二产业中以能源密集型产业为主，长期的粗放型增长带来大量的能源浪费。因此第二产业比重的增加势必带来能源消费量的增加，从而产生更多的碳排放量。因此各地区应积极优化产业结构，大力扶持和发展第三产业，降低第二产业在整个经济产出中的比重，以达到降低污染，减少碳排放量的目的。

除产业结构外人口规模对碳排放量的影响也是正的，我国是一个人口大国，人口基数大是我国的一个基本国情，近年来各地区的人口自然增长率均已得到控制，但人口自然增长率降低引发的新问题是人口老龄化现象严重，尽管人口老龄化对于碳排放量有一定程度的抑制作用，但依靠增加老年人口比重来减少碳排放量并不是理想的选择。

3. 技术水平对碳排放量的影响是负的，技术水平的提高将带来碳排放量的减少

技术水平对碳排放量的抑制作用主要是通过提高能源利用效率来实现，特别是通过新技术的应用和新设备的研发来提高能源的利用效率，达到减少能源使用和减少碳排放量的目的。另一方面新能源的开发和应用也将大幅度降低能源的消费量，开展能源节约、资源循环利用、发展绿色科技，从而达到降低碳排放量的目的。此外，技术进步也会带来经济增长方式的转变，促进产业结构的优化，从而间接地减少碳排放量。因此应加速技术进步的步伐，鼓励新技术的应用和新产品的研发，积极引进先进的设备和技术是减少碳排放量积极有效的途径。

4. 城市化率对碳排放量的影响不显著

城市化率对碳排放量的影响具有双向性。一方面，城市化率的提高使得城市基础设施建设增加，使得建筑材料需求增加，居民日常生活和供暖等都需要更多的能源消费，从而增大碳排放量。另一方面，由于城市化率的提高，使得人口和经济要素的集聚，能源利用效率提高，以及城市化所带来的知识和技术等溢出效应使碳排放量得以减少。人口结构对碳排放量的影响尽管不是很显著，但是人口老龄化现象严重是我国目前面临的另外一个严峻的人口问题。因此各级地方政府在制定人口政策时应立足于本地区的实际情况，根据自身区域经济和人口发展的特点采取相应的人口政策、生育政策来促进本区域乃至全国人口结构的优化。

5. 能源消费结构对碳排放量的影响也不显著

煤炭消费占能源消费总量比重的增加会带来碳排放量的增加。其原因在于煤炭的碳排放系数较大，因此煤炭消费所产生的碳排放量比其他能源消费所产生的碳排放量大。尽管我国各地区的能源消费结构相差较为悬殊，但是大部分地区的能源消费以煤炭为主，水能、电能、风能等清洁能源所占的比重较低。北京、上海等经济发达地区的煤炭消费占能源消费比重在40%左右，而山西、内蒙古、贵州、重庆等地区的煤炭消费占能源消费比重在80%以上。应鼓励提高清洁能源在能源消费总量中的比重。此外还应该积极提高地热和太阳能等清洁、可再生能源的开发力度，达到减少碳排放量，提高环境质量的目的。

[1] Ehrlich P R, Holdren J P. Impact of population growth[J]. Science, 1971, 171(3977): 1212−1217.

[2] Dietz T, Rosa E A. Rethinking the environmental impacts of population, affluence and technology[J]. Human Ecology Review, 1994(1): 277−300.

[3] Mackellar L F, Lutz W, Prinz C, et al. Population, households and CO2emissions[J]. Population and Development Review, 1995, 21(4): 849−865.

[4] York R, Rosa E A, Dietz T. Footprints on the earth the environmental consequences of modernity[J]. American Sociological Review, 2003,68(2): 279−300.

[5] 肖宏伟, 易丹辉, 张亚雄. 中国区域碳排放空间计量研究[J].经济与管理, 2013, 27(12): 53−62.

[6] 宋德勇, 刘习平. 中国省际碳排放空间分配研究[J]. 中国人口·资源与环境, 2013, 23(5): 7−13.

[7] Wang C, Chen J, Zou J. Decomposition of energy-related CO2emission in China:1957−2000[J]. Energy, 2005, 30(1): 73−83.

[8] Wu L, Zeng W. Research on the contribution of structure adjustment on carbon dioxide emissions reduction based on LMDI method[J]. Procedia Computer Science, 2013, 17: 744−751.

[9] Ren S, Yin H, Chen X. Using LMDI to analyze the decoupling of carbon dioxide emissions by China's manufacturing industry[J]. Environmental Development, 2014, 9(1): 61−75.

[10] 范丹. 中国能源消费碳排放变化的驱动因素研究——基于 LMDI-PDA分解法[J]. 中国环境科学, 2013, 33(9): 1705−1713.

[11] 许海平. 空间依赖、碳排放与人均收入的空间计量研究[J]. 中国人口·资源与环境, 2012, 22(9): 149−157.

[12] Stern D I, Common M S. Is there an environmental Kuznets curve for sulfur?[J]. Journal of Environmental Economics and Management, 2001, 41(2): 162−178.

[13] Galeotti M, Lanza A. Desperately seeking environmental Kuznets[J]. Environmental Modelling & Software, 2005, 20(11): 1379−1388.

[14] Richmond A K, Kaufmann R K. Energy prices and turning points: The relationship between income and energy use/carbon emissions[J]. The Energy Journal, 2006, 27(4): 157−179.

[15] Song T, Zheng T, Tong L. An empirical test of the environmental Kuznets curve in China: A panel cointegration approach[J]. China Economic Review, 2008, 19(3): 381−392.

[16] 王建军, 周晓唯. 人口、能源消耗、碳排放与经济增长关系实证分析[J]. 统计与决策, 2013(23): 114−117.

[17] 杜慧滨, 李娜, 王洋洋, 等. 我国区域碳排放绩效差异及其影响因素分析——基于空间经济学视角[J]. 天津大学学报(社会科学版), 2013, 15(5): 412−416.

[18] 陈德湖, 张津. 中国碳排放的环境库兹涅茨曲线分析——基于空间面板模型的实证研究[J]. 统计与信息论坛, 2012, 27(5): 48−53.

[19] York R, Rosa E A, Dietz T. Bridging environmental science with environmental policy: Plasticity of population, affluence, and technology[J]. Social Science Quarterly, 2002, 83(1): 18−34.

[20] Cole M A, Neumayer E. Examining the impact of demographic factors on air pollution[J]. Population and Environment, 2004, 26(1): 5−21.

[21] Dietz T, Rosa E A. Effects of population and affluence on CO2emissions[J]. Proceedings of the National Academy of Sciences, 1997, 94(1): 175−179.

[22] York R, Rosa E A, Dietz T. Stirpat, ipat and impact: Analytic tools for unpacking the driving forces of environmental impacts[J]. Ecological Economics, 2003, 46(3): 351−365.

[23] 彭希哲, 朱勤. 我国人口态势与消费模式对碳排放的影响分析[J]. 人口研究, 2010, 34(1): 48−58.

[24] Alvydas B, Tomas B, Dalia S. The energy intensity in Lithuania during 1995－2009: A LMDI approach[J]. Energy Policy, 2011, 39(11): 7322−7334.

[25] 黄芳, 江可申, 卢愿清, 等. 中国碳强度的影响因素分析——基于LIMDI 分解方法[J]. 数学的实践与认识, 2012, 42(6): 40−42.

[26] 李丹丹, 刘锐, 陈动. 基于空间聚类分析的中国省域能源消费碳排放分布特征研究[J]. 北京师范大学学报(自然科学版), 2013, 49(5): 529−533.

[27] 程叶青, 王哲野, 张守志, 等. 中国能源消费碳排放强度及其影响因素的空间计量[J]. 地理学报, 2013, 68(10): 1418−1431.

[28] 吕健. 城市化驱动经济增长的空间计量分析: 2000−2009[J]. 上海经济研究, 2011(5): 3−15.

[编辑: 谭晓萍]

Analysis of factors affecting carbon emissions based on spatial econometrics

FU Yunpeng, MA Shucai

(School of Economics, Liaoning University, Shenyang 110036, China)

The present study, based on the estimate of the carbon emissions of 30 provinces in China from 2000 to 2014, tests the spatial autocorrelation of carbon emissions by exploiting Moran's I Index. On this basis, the extended STIRPAT Model is taken as the theoretical perspective and spatial regression model is employed in studying the effect of demographic structure, industry structure, energy structure, technological level and other factors on carbon emissions. The result shows that industry structure, demographic structure, and technological level are the main influential factors on carbon emissions, and that the effect of industry structure and demographic size is positive while that of technical level is negative.

demographic size; industry structure; technological level; spatial autocorrelation; spatial regression model

F061.5

A

1672-3104(2017)02−0103−08

2016−11−30；

2017−01−14

国家社科基金青年项目“基于空间计量分析的人口规模、结构对资源环境的影响效应研究”(13CRK027)；中国博士后科学基金第60批面上项目“中国居民消费碳排放量及其影响因素的空间计量分析”(2016M601327)；辽宁省教育厅科学研究一般项目“辽宁资源环境承载力的时空特征研究”(W2015171)

付云鹏(1978−)，女，满族，辽宁铁岭人，统计学博士后，辽宁大学经济学院副教授，主要研究方向：资源经济学，计量经济模型及其 应用