价值实现视角下技术入股合作的机理分析

张根明，王婧



价值实现视角下技术入股合作的机理分析

张根明，王婧

(中南大学商学院，湖南长沙，410083)

在技术入股合作中，由于合作双方行为的不确定性和不合理的技术入股比例，合作难以达到预期效果。通过分析合作存在的事后道德风险，运用演化博弈方法建立技术方与资本方的博弈模型，研究影响技术入股合作效果的因素。研究表明技术入股比例、合作双方的诚意以及专业能力是不同情境下影响合作效果的重要因素；合理的技术入股比例由技术价值与合作双方的专业能力共同决定。

技术入股合作；技术价值；技术入股比例；演化博弈；事后道德风险

一、引言

科技成果是创新创业的基础，也是推进供给侧结构性改革的重要内容。而我国科技成果转化率仅为10%，实现产业化的不到5%，远低于发达国家40%的水平[1]。技术入股合作是技术提供方投入阶段性研究成果和后续研发力量，资本提供方投入资金和市场能力，共同组建股份有限公司或有限责任公司，开发新产品并投入市场，最后按照合同规定的入股比例分享收益[2]。技术入股合作能集中各参与方的优势资源，通过合作，技术方能缓解科技成果不能适应市场需求的情况，提高科技成果转化率。资本方可以利用优势研发资源、降低技术风险以及缩短产品研发周期[3]。

技术入股合作虽能提高创新绩效和科技成果转化效率，但由于其本身存在的一系列问题，技术入股在我国并未取得预期的效果。多数学者认为，在我国实现技术入股，一方面，存在股权归属不清，技术入股审批、备案程序复杂，强制性技术入股评估作价不尽合理及资产管理落后等障碍[4−6]；另一方面，合作过程中存在道德风险以及逆向选择问题，张米尔等认为在技术入股产学研合作中，高校或科研机构将面临来自企业的道德风险[7]。郭亮玺等认为技术入股存在技术提供方风险、资本提供方风险以及双方面临的道德风险[8]。柴国荣等认为由于信息不对称，技术提供方可能会提供成功率较低的技术，导致技术入股合作存在逆向选择问题，最后证明技术入股比例的信号传递作用和信誉机制对于促进技术入股合作意义重大[2]。关于合作的利益分配问题一直是学者关注的焦点，Nash运用公理化方法求得讨价还价类问题的Nash协商解，用以解决合作项目利益分配问题[9]。Nishizaki等运用含模糊参数的数学规划求解优化模型，构建联盟利益分配机制[10]。Flamsd等分析了联盟企业在共享技术、任务、禀赋情形下成本转移的博弈行为，得出成本最小情况下的利益分配形式[11]。Lai等从企业研发外包的角度出发，利用委托代理理论设计收益共享合同，以节约外包成本，激励接包方努力工作[12]。罗利等用博弈论的方法分析产学研合作中的利益分配问题，并论述了用Shapley值法求解利益分配问题需要满足的公理条件[13]。鲍新中等认为企业通过技术创新成本补贴方式可以刺激学研方技术创新，运用Rubinstein的子博弈精炼均衡结果可以对合作创新超额利润进行再次分配[14]。刘云龙等认为合作收益分配系数是努力水平程度、努力成本系数的增函数，随着研发深入，努力水平的贡献系数越大，其努力成本系数也越大[15]。以上学者对合作利益分配问题进行了广泛探讨，多侧重于委托开发与合作开发模式，而技术入股模式下的合作利益分配仍需深入研究。

目前技术入股合作的研究以定性分析居多，主要分析合作存在的法律问题。定量研究多以信息经济学和博弈论为基础，分析信息不对称时，资本提供方在面临事前道德风险(技术提供方可能提供差的技术)情况下采取“合作”或“不合作”两种策略。但是合作启动后，各行为主体仍有可能采取投机行为，损害合作方利益，实践中确定技术入股比例时仅考虑技术价值在总资产价值中的份额，忽略合作双方的行为对价值实现的影响，合作易产生事后道德风险。本文从技术价值实现的视角，分析合作中的事后道德风险，研究技术入股比例与合作行为主体策略选择的影响因素，具有理论意义和实践价值。

二、技术入股合作机理分析与模型建立

(一)概念界定

1. 合作行为主体

技术入股合作主要包括技术方和资本方两个行为主体。

(1) 技术方。技术方提供技术专利或阶段性技术成果并投入后续研发力量。本文讨论的技术方主要是高校和科研机构，因高校和科研机构在知识掌握上没有本质区别，本文不进行严格区分。

(2) 资本方。资本方投入资金和市场能力并参与经营管理。在技术入股合作中，资本方一般是中小型制造企业，中小型制造企业需要借助外力提高研发 能力。

2. 技术价值

技术价值是产生合作收益的基础，本文特指技术的评估价值，即由独立的第三方机构利用其专业知识，以未来产品收益的合理预测为基础，对入股技术价值的评估值。

3.技术入股比例

即技术方以专利或科技成果入股时与资本方商定的持股比例。技术入股比例的设定具有不确定性，关系到合作利益的分配，是本文研究的重点。

(二)合作及道德风险产生机理分析

根据邢小强和仝允桓的观点，技术未被使用时并不产生价值, 只有当该技术与其他补充性资产相结合而进行商业化并创造效益时，技术价值才得到体 现[16]。技术入股合作是一个技术价值实现的过程。从技术研究到工业化生产，还包含产品的构思设计与试制、中间实验、建立中试基地、持续改进产品质量等过程。它们关系到技术能否转化为产品并实现其商业价值。不同于技术买断，技术方提供技术或专利后，还需投入后续研发力量，派遣技术人员不断进行中试和改进，完成由实验室研究成果到产品方案的转化。资本方投入资金设备和劳动力，生产和销售产品实现商业化。合作中，一方面，由于信息不对称，技术方和资本方的努力程度难以观测和监督，而努力均需付出成本，因此双方都有可能采取投机行为，减少自身投入以谋取私利[17]。另一方面，技术入股比例一般是事先商定的，即技术价值占投入总资产的比例，因此合作易产生道德风险。合作过程中技术方可将技术卖给多家，使该技术失去垄断优势，或者在中试和改进过程中消极怠工采取不作为的行为，降低产品化成功率。资本方可通过关联交易转移利润，无偿占有公司经济资源或以较少的出资占有较多的股份，或者采取不作为的行为，导致合作收益降低。

综上所述，技术方和资本方的行为会影响技术价值的实现，从而影响合作收益[18]。信息不对称和现行持股比例确定方法使合作双方面临事后道德风险。据此，建立如下技术方和资本方行为的博弈模型。

(三)演化博弈模型的建立

1.模型基本假设

(1) 第三方资产评估机构能对技术价值进行客观公正的评估。

(2) 在合作过程中，技术方与资本方的策略空间都是(努力，不努力)。其中，“努力”是指合作方按合同约定投入人力、物力和财力，“不努力”则是在合作时采取消极怠工，减少投入等违反合同约定的行为。只有在合作双方都努力的情况下，技术价值才能实现。

(3) 设是产品化成功率，反映技术方专业能力。是技术方努力成本的函数，且>0。是资本方将技术价值转化为合作产品收益的转化因子，反映资本方的生产和销售能力。是资本方努力成本的函数，且>0。由于生产工艺和市场规模的变化，，值也会发生变化。

(4) 技术方和资本方都是有限理性群体，具有有限的决策能力和选择能力，只能通过试错的方法达到博弈均衡。假设在博弈的初始时刻，资本方采取努力策略的概率为，采取不努力策略的概率为1−；技术方努力的概率为，不努力的概率为1−；，∈[0,1]。

2. 模型的建立

设为双方协商的技术方持股比例，1−为资本方持股比例，0<<1；是技术价值；1，2分别是技术方在努力和不努力状态下的产品化成功率，1≥1>2≥0；1，2分别表示资本方在不同行为下的转化因子，1>2≥0；设是合作收益。根据假设3，=。是产品化成功率，所以11，12，21，21是技术方和资本方在不同行为状态下的合作 收益。

1，2分别是技术方在不同努力状态下付出的成本，1>2>0；1，2分别是资本方在不同行为下的成本，1>2>0；是技术方的违约成本；是技术方不努力被资本方发现的概率，∈[0,1]；是资本方违约成本；是资本方不努力被技术方发现的概率，∈[0,1]。表1为技术方和资本方的创新博弈矩阵。

表1 技术入股合作创新博弈矩阵

三、资本方与技术方的演化博弈分析

(一)复制动态方程

根据表1的资本方和技术方的支付矩阵，分别得到以下复制动态方程。

1.资本方

努力策略的期望收益为：11=[(1−)11−1]+(1−)[(1−)21−1+]；不努力策略的期望收益为：12=[(1−)12−2−]+(1−)[(1−)22−2−+]；努力与不努力的平均期望收益为：1=11+ (1−)12。资本方的复制动态方程为：

()=d/d=[11−1]=(1−){(1−)(1−2)(1−2)−[(1−)2(2−1)+1−2−]}

′()=(1−2){(1−)(1−2)(1−2)–[(1−)2(2−1)+1−2−]}

2.技术方

努力策略的期望收益：21=[11−1]+ (1−)[12−1+]；不努力策略的期望收益为：22=[21−2−]+(1−)[22−2−+]；努力与不努力的平均期望收益为：2=21+(1−)22。技术方的复制动态方程为：

()=d/d=[21−2]=(1−){(1−2)(1−2) – [2(2−1)+1−2−]}

’()=(1−2){(1−2)(1−2)−[2(2−1)+1−2−]}

分别令()，()等于零。求得均衡点：1(0，0)，2(0，1)，3(1，0)，4(1，1)，5(0，0)，其中：

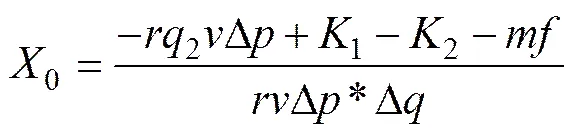
Δ=1−2, Δ=1−2；(1) 只有当0，0∈[0,1] 时，5才存在。

(二)稳定性分析

根据演化博弈稳定策略的性质，当'()<0 时，为演化稳定策略。据此，讨论资本方和技术方的策略演化稳定情况。

1. 资本方策略的稳定性分析

(1)当(1−)2(2−1)+1−2−>0，且(1−)2(2−1)+1−2−<(1−)(1−2)(1−2)时，得(1−)1(2−1)+1−2−<0，此时0<0<1，满足：<1−<。根据演化稳定策略的判别原则，当技术方选择努力策略的初始概率>0时，′(1)<0，=1是演化稳定策略。即当技术方采取努力策略的概率大于一定值时，有限理性的资本方会选择努力。当<0，′(0)<0,=0是演化稳定策略，即当技术方采取努力策略的概率小于一定值时，有限理性的资本方最终会选择不努力策略。当=0时，资本方不存在稳定策略。

(2)当(1−)2(2−1)+1−2−<0时，由(1−)(1−2)(1−2)恒大于零，得(1−)1(2−1)+1−2−<0，0<0，满足1−>。对任意∈[0,1]，总有(1)<0，1是演化稳定策略，即无论技术方策略如何，资本方都会采取努力策略。

(3)当(1−)2(2−1)+1−2−>0，且(1−)2(2−1)+1−2−>(1−)(1−2)(1−2)，得(1−)1(2−1)+1−2−>0，0>1。满足1−<。对任意[0,1]，总有(0)<0，=0是演化稳定策略。即无论技术方策略如何，资本方最终会选择不努力。

2.技术方策略的稳定性分析

当2(2−1)+1−2−>0且2(2−1)+1−2−<(1−2)(1−2)时，得1(2−1)+1−2−<0，此时0<0<1，满足<<。根据演化稳定性的判别原则，当资本方选择努力策略的初始概率>0时，′(1)<0，=1是演化稳定的策略，即当资本方采取努力策略的概率大于一定值时，有限理性的技术方会选择努力。当<0，′(0)<0，=0是技术方稳定的策略，即当资本方采取努力策略的概率小于一定值时，有限理性的技术方不会努力；当=0时，资本方不存在稳定策略。

(2)当2(2−1)+1−2−<0时，由(1−2)·(1−2)恒大于零得：1(2−1)+1−2−<0。0<0，满足>。对任意∈[0,1]，总有′(1)<0，=1是演化稳定策略。即无论资本方采取何种策略，技术方最终都会选择努力。

(3)当2(2−1)+1−2−>0，且2(2−1)+1−2−>(1−2)(1−2)时，可得1(2−1)+1−2−>0。0>1，满足<。对任意∈[0,1]，总有′(0)<0，=0是演化稳定策略，即无论资本方选择何种策略，技术方最终都会选择不努力。

3.技术方和资本方的博弈结果配对

把上述几种情况分别配对，如表2所示。

表2 资本方和技术方不同条件组合下的演化稳定均衡点

为促进技术价值的实现，激励资本方和技术方更好地合作，提高社会创新水平，4(1,1)是本文研究追求的稳定均衡点。由表2得到以下结论。

(1) 当资本方和技术方均满足条件一时，博弈结果取决于对方的合作诚意，即博弈初始时刻对方努力的概率。当一方努力的概率大于某一特定值时，最终双方都会选择努力策略。由表达式(1)得，该特定值与合作方专业能力相关，在其他条件不变的情况下，，，Δ，Δ值越大，0，0越小，实现策略(1,1)的可能性越大。

(2) 当技术方和资本方中任意一方满足条件二，另一方不满足条件三时，因此合作双方都会选择努力策略，实现帕累托最优。此时技术持股比例满足最优入股比例区间：∈U①。反之，只要一方满足条件三，技术方和资本方通力合作的结果将不会出现。

四、数值算例的仿真分析

为了更直观地反映上文对资本方和技术方的策略稳定性分析，下面运用matlab7.0就具体算例的策略演化情况进行仿真模拟。

算例：某高校(技术方)与某制造企业(资本方)进行技术入股合作，该企业与高校协商的技术价值为50万元，协定高校投入该技术并在合作中派遣相关研发人员进行中试与技术改进和更新，企业投入资金400万元，高校持股比例为20%。

(一)阶段一

市场不成熟，资本方转化能力较低。参数值如下：=50，1=0.7，=20%，2=0.3，1=20，2=10，1=400，2=200，1=105，2=45，=0.05，=0.01，=100，=100，根据假设4，可根据联合国公布的行业技术提成率(销售额提成率)得出[19]。根据表达式(1)可得0=0.375，0=0.49375。0<0<1，0<0<1，资本方和技术方均满足条件一。运用matlab7.0模拟二者策略的动态演化过程。

1. 资本方的策略演化情况

取=0.5>0，资本方的策略演化情况如图1所示：当>0.4975时，→1。即当技术方选择努力策略的初始概率大于0.4975时，资本方最终采取努力策略。

取=0.3<0，资本方的策略演化情况如图2所示：当<0.4975时，→0。即当技术方选择努力策略的初始概率小于0.4975时，资本方最终采取不努力策略。

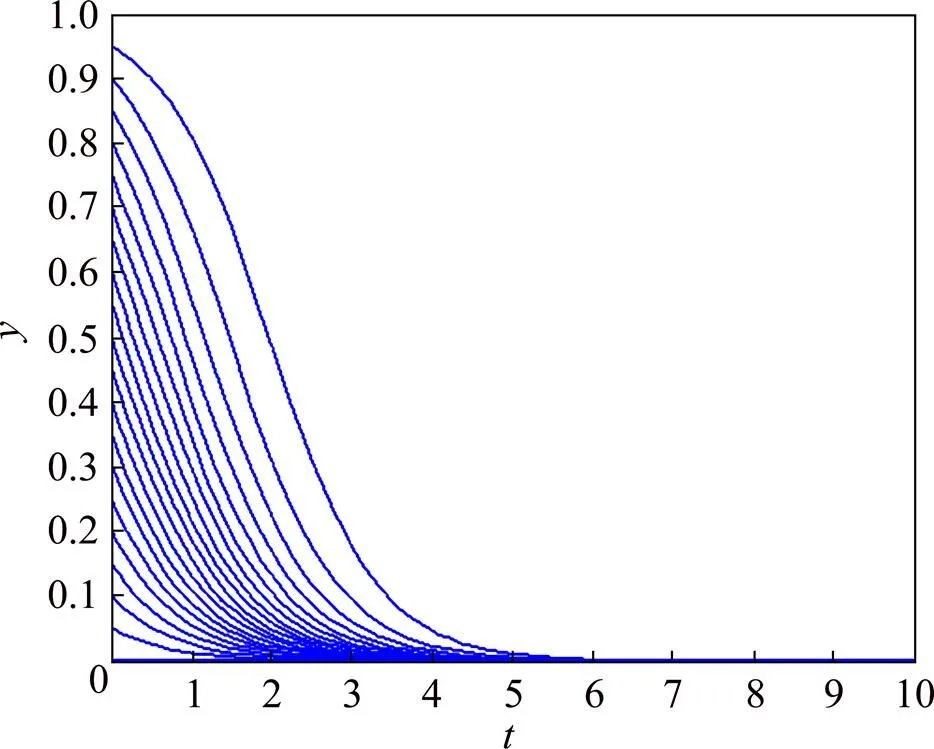
图2 资本方策略的动态变化

2. 技术方策略的进化情况

取=0.4>0，技术方的策略演化情况如图3所示：当>0.375时，→1。即当资本方选择努力策略的初始概率大于0.375，技术方最终会采取努力策略。

图3 技术方策略的动态变化

取=0.3<0，资本方的策略演化情况如图4所示：当<0.375时，→0。即当资本方选择努力策略的初始概率小于0.375时，技术方最终会采取不努力策略。

3. 综合分析结果

将上述对技术方和资本方的分析综合起来，得到以下结果：即当资本方和技术方均满足条件一时，点(0, 0)和点(1, 1)是演化稳定点，如图5所示。最终结果为合作双方要么都努力，要么都不努力，取决于博弈初始时刻资本方和技术方采取努力策略的概率。

(二)阶段二

市场日趋成熟，规模经济产生，同等投入下资本方转化能力增强：1=40，2=20，其他条件不变。计算可得0=−0.3125<0，0=−0.1281<0。资本方入股 比例1−>，技术方持股比例>。博弈双方均满足条件二，技术持股比例满足最优入股比例区间。

图4 技术方策略的动态变化

图5 条件一组合技术方和资本方策略稳定情况

1. 资本方的策略稳定性分析

任意选取的一系列值，得到图6：无论y取何值，→1，努力是资本方的不变策略，即无论技术方初始时刻采取努力策略的概率大小，资本方最终都会采取努力策略。

2.技术方的策略稳定性分析

任意选取的一系列值，得到图7：无论取何值，→1，努力是技术方的不变策略，即无论资本方初始时刻采取努力策略的概率大小，技术方最终都会采取努力策略。

图6 资本方策略的动态变化

图7 技术方策略的动态变化

3.综合两方博弈策略分析

如图8所示：(1，1)是唯一的进化稳定点，资本方和技术方最终均采取努力策略，实现帕累托最优。

图8 条件二组合技术方和资本方的策略稳定情况

上述仿真主要分析了两种情境下资本方和技术方策略动态演化情况。从而验证：技术入股比例是决定合作成功的关键因素。当技术持股比例满足最优比例区间时，资本方和技术方均选择努力策略，合作成功。若技术入股比例不满足最优区间但满足条件一时，双方合作诚意是决定合作成功的关键因素。同时，合作双方的专业能力也会影响合作双方的策略选择。在其他条件不变的情况下，，，Δ，Δ越大，合作双方选择努力策略的可能性越大。

五、结论

本文运用演化博弈理论构建了技术入股合作的博弈模型，并分析合作的演化稳定性。结论如下：

(1) 技术入股比例是决定合作成功的关键因素。赢利是理性决策者的首要考虑因素，合适的入股比例是双方通力合作的基础。当技术持股比例满足最优比例区间时，资本方和技术方努力比不努力更有利，双方都会选择努力策略，实现帕累托最优。最优持股比例应综合考虑技术价值和合作方的专业能力。因此资本方和技术方在决定合作前，首先应对合作方进行调查，考察其专业能力和信誉度，与对方商定合适的持股比例；其次，合作协议中应注明首次合作成功后，合作双方应根据各方表现调整技术入股比例。

(2) 当技术入股比例难以满足最优比例区间但合作双方均满足条件一时，合作诚意决定合作成功。只要对方能表现出合作的诚意，以较大的概率采取努力策略，自己采取努力策略就是有利的，合作继续。因此，作为资本方的企业，在实务中需要加强对技术方的监督，观察对方的诚意，在成本允许范围内多进行产品测试。此时双方不应在入股比例上做过多要求。资本方和技术方的专业化能力也会影响合作效果。

同时，在其他条件不变的情况下，专业能力越高，双方信任度增强，合作成功的可能性越大。

注释：

① 最优技术入股比例区间的计算：

入股比例应使资本方和技术方中任意一方满足条件二，另一方不满足条件三，分以下几种情况讨论。

A. 资本方满足条件二，技术方不满足条件三。

B. 技术方满足条件二，资本方不满足条件三。

[1] 2014−2018年中国科技成果转化行业全景调研与发展趋势预测报告[DB/CD]. 中国报告大厅, 2014, 3.

[2] 柴国荣, 徐渝, 叶小青. 技术入股合作创新的市场均衡模型及其管理含义[J]. 科学学与科学技术管理, 2005(3): 34−37.

[3] Howells J, Gagliardi D, Malik K. The growth and management of R＆D outsourcing: Evidence from UK pharmaceuticals[J]. R&D Management, 2008, 38(2): 205−219.

[4] 赵捷, 张杰军, 汤世国, 等. 科技成果转化中的技术入股问题研究[J]. 科学学研究, 2011, 29(10): 1485−1489.

[5] 刘彦蕊, 丁明磊, 管孟忠. 科研事业单位技术类无形资产入股问题探析[J]. 科学学研究, 2015, 33(6): 876−880.

[6] 刘伟, 杨麒渊, 童洪志. 科技成果资产证券化途径及其策略研究[J]. 科技管理研究, 2015(15): 23−27.

[7] 张米尔, 武春友. 技术入股型产学研合作创新的道德风险[J]. 研究与发展管理, 2001, 13(2): 29−31.

[8] 郭亮玺, 周燕. 技术成果入股的风险识别与防范模型[J]. 技术经济与管理研究, 2006(5): 39−40.

[9] NASH J F. The bargaining problem[J]. Econometrica, 1950, 18(2): 155−162.

[10] Nishizaki, Sakawa M. Solutions based on fuzzy goals in fuzzy linear programming games[J]. Fuzzy Sets and Systems, 2000, 115(1): 105−119.

[11] Flamsd, Jourania. Strategic behavior and partial cost sharing[J]. Games and Economic Behavior, 2003, 43(1): 44−56.

[12] LaiEL C, Riezman R, Wang P. Outsourcing of innovation[J]. Economic Theory, 2009, 38(3): 485−515.

[13] 罗利, 鲁若愚. Shapley值在产学研合作利益分配博弈分析中的应用[J]. 软科学, 2001, 15(2): 17−93.

[14] 鲍新中, 王道平. 产学研合作创新成本分摊和收益分配的博弈分析[J]. 研究与发展管理, 2010, 22(5): 75−81.

[15] 刘云龙, 李世佼. 产学研联盟中合作成员利益分配机制研究[J]. 科技进步与对策, 2012, 29(3): 23−25.

[16] 邢小强, 仝允桓. 实物期权法评估技术价值及其管理涵义[J].科学学与科学技术管理, 2006(4): 23−27.

[17] Kultti K, Takalo T. Incomplete contracting in all R＆D project: The micronas case[J]. R&D Management, 2000, 30(1): 67−76.

[18] 黄波, 孟卫东, 李宇雨. 基于双边激励的产学研合作最优利益分配方式[J]. 管理科学学报, 2011, 14(7): 31−42.

[19] 冯丽艳. 专利价值评估中技术分成率的确定方法[J]. 商业会计, 2011(1): 46−47.

[编辑: 谭晓萍]

Mechanism analysis of technology-stock cooperation:From the value realization perspective

ZHANG Genming, WANG Jing

(School of Business, Central south university, Changsha, Hunan, 410083)

Because of the uncertain behaviors and unreasonable technical shareholdings on both sides in their technology−stock cooperation, it becomes hard for cooperation t to achieve the desired effect. On the basis of analyzing the existence of afterwards moral hazards of the cooperation, the present essay builds an evolutionary game model between technology provider and capital provider to discuss the factors affecting the effect of technology−stock cooperation. The research findings indicate that technology shareholding, sincerity for cooperation and professional competence of both sides are important factors affecting cooperation process in different situations. Reasonable technology shareholding should be decided by technical assessment value, professional competence of both parties.

technology-stock cooperation; technology assessment value; technology shareholding; afterwards moral hazard; evolutionary game

F274.5

A

1672-3104(2017)02−0120−07

2016−12−10；

2017−02−07

国家自然科学基金项目“复杂环境下我国企业突破性技术创新资源配置优化研究”(71172100)；国家软科学研究计划“制约创新驱动发展的重点问题及建议研究”(2014GXS4D135)

张根明(1963−)，男，湖南长沙人，中南大学商学院教授，博士生导师，主要研究方向：创新与创业管理；王婧(1992−)，女，湖南长沙人，中南大学商学院硕士研究生，主要研究方向：创新与创业管理