具损失厌恶和损失概率厌恶的报童问题研究

马德青,胡劲松，姜 伟，陈 良

(1.青岛大学商学院,山东 青岛 266071；2.青岛大学经济学院,山东 青岛 266071)

具损失厌恶和损失概率厌恶的报童问题研究

马德青1,胡劲松1，姜 伟2，陈 良1

(1.青岛大学商学院,山东 青岛 266071；2.青岛大学经济学院,山东 青岛 266071)

研究了具损失厌恶和损失概率厌恶行为的考虑缺货成本报童模型。利用订购量小于和大于最大损失等量订购量时的随机利润分布函数以及随机获利和损失的排名函数，获得了报童的前景值函数，分析了报童的前景值函数性质。结果表明：前景值函数为订货量的连续不可微凹函数，不可微点位于最大损失等量订购量处；而且仅具损失厌恶或仅具风险中性的报童模型是本模型的特例。解析分析表明：当最优订购量小于最大损失等量订购量时，最优订购量随极端获利和不利结果重视程度的提高而增加；当最优订购量大于最大损失等量订购量时，最优订购量随极端获利结果重视程度的提高而增加，最优订购量随极端不利结果重视程度的提高而减少。数值结果表明：最优订购量随非极端获利和非极端损失结果敏感度的提高而增加；最优订购量随损失厌恶系数的提高而减少。

报童问题;前景理论;损失厌恶;损失概率厌恶

1 引言

报童模型作为易逝品管理的经典分析模型，国内外学者对其进行了广泛深入的研究，例如最新的国内研究成果有陈杰等[1]，张永等[2]，陈杰等[3]，但这几篇文献都没有考虑损失厌恶和损失概率厌恶。报童模型的有效性关键取决于企业风险行为的刻画。现有研究多从风险结果价值判断的角度去分析企业风险行为，而较少从风险结果发生概率的角度去分析企业风险行为。事实上，大量行为心理实验揭示：面对风险决策时，人们不仅存在风险结果价值判断上的参考依赖效应以及符号依赖效应(或称损失厌恶)[4-5]，而且还存在风险结果发生概率上的排名依赖效应[6]和符号依赖效应(或称损失概率厌恶)[7]。

近来，国内外学者针对报童的损失厌恶行为开展了专题性研究，但针对报童的损失厌恶概率行为缺乏分析模型。在具损失厌恶行为报童问题的专题性研究中，Chweitzer和Cachon[8]和文平[9]究发现具损失厌恶行为报童的最优订货量低于风险中性报童的订货量。Wang和Webster[10]研究了含缺货成本的具损失厌恶行为报童问题，发现缺货成本较高时具损失厌恶行为报童的订货量将高于风险中性报童。随后，国内外学者围绕损失厌恶行为，从多角度开展了深化研究。其中，Shen Houcai等[11]研究了定制件采购决策问题中的损失厌恶报童行为。周永务等[12]研究了损失厌恶零售商的广告费用和订货量的联合决策问题。柳键等[13]研究了顾客存在损失厌恶情形时零售商的订货和定价策略。Baron等[14]在顾客存在损失厌恶情形时研究了基于随机参考点的报童订购决策问题。张鹏等[15]研究了在加法需求和乘法需求两情形下的损失厌恶行为零售商最优决策问题。周艳菊等[16]从心理参考点、损失厌恶系数、风险态度系数等多个角度研究了两产品报童问题。Geng Wei等[17]研究了具S型指数效用函数的损失厌恶决策者最优行为，发现损失厌恶决策者订货量亦低于风险中性决策者订货量。

值得指出的是，近来有关学者将损失厌恶行为纳入到供应链和供应链网络成员决策制定问题中。其中，针对供应链，刘咏梅等[18]研究了风险中性供应商和具有损失厌恶零售商组成供应链的弹性数量契约问题；针对供应链网络，胡劲松等[19]针对模糊市场需求研究了中性供应商层和具有损失厌恶零售商层组成的供应链网络的成员均衡策略。上述文献均为损失厌恶行为的专题性研究，均未涉及损失概率厌恶行为。

近期，胡劲松等[20]针对不考虑缺货成本的零售商，构建了具损失概率厌恶和损失厌恶行为零售商目标效用函数，研究了具损失概率厌恶和损失厌恶行为零售商的供应链网络均衡问题。当零售商考虑缺货成本时，由于零售商的利润函数存在两个盈亏平衡点，进而可能会破坏具损失概率厌恶和损失厌恶行为零售商目标效用函数的可微性。为此，本文围绕报童模型，揭示考虑缺货成本的具损失概率厌恶和损失厌恶行为报童的目标效用函数性质，建立具损失厌恶和损失概率厌恶行为的考虑缺货成本报童问题分析模型。

2 数学模型

2.1记号与假设

设c为单位产品采购费；h为单位产品存储费；s为单位产品缺货费，假设单位产品缺货费s为有限值；p(>c)为单位产品售价；Q为订购量。

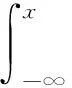
假设3 报童是损失厌恶者，其价值函数:

式中，u(x)为其基础效用函数，λ(≥1)为其损失厌恶系数。

损失厌恶系数λ反映了报童的厌恶程度，λ值越大，其损失厌恶程度越高。特别地，当λ=1时，报童的价值函数取基础效用函数。由于市场随机需求和单位产品缺货费的有限性，报童的最大获利为(p-c)xmax，其最大损失为sxmax∨(h+c)Q。事实上，报童的随机利润的取值总为有限区间[-(sxmax∧(h+c)Q),(p-c)xmax]，所以进一步假设报童的基础效用函数u(x)=x。

假设4 报童是对极端结果敏感、对非极端结果不敏感的损失概率厌恶行为者。即报童具有如下获利权重函数w+(r)和损失权重函数w-(l)，参见图1。

其中，参数r表示获利排名；参数γ+表示报童对最大获利的重视程度；参数δ+表示报童对获利概率的敏感性；各参数满足γ+，δ+≥0，γ++δ+≤1。参数l表示损失排名；参数γ-表示报童对最大损失的重视程度；参数δ-表示报童对损失概率的敏感性；各参数满足γ-，δ-≥0,γ-+δ-≤1。

获利排名参数r和损失排名参数l反映了风险结果的排名依赖效应。参数γ+和γ-反映了最好和最坏极端结果的重视程度，其取值越大，报童对最好和最坏极端越重视。参数δ+和δ-反映了报童对非极端的概率不敏感性倾向。事实上，参数γ+和γ-刻画了人们在风险价值评价中存在的可能性效应，而参数1-γ+-δ+和1-γ--δ-刻画了人们在风险价值评价中存在的确定性效应。

所谓损失概率厌恶行为是指相较于获利的发生，人们更加重视损失的发生的一种行为。为此假设γ-≥γ+,即人们重视不利极端结果的发生，此外假设δ-≥δ+，即相较于非极端获利人们更重视非极端损失的发生。事实上，γ-≥γ+和δ-≥δ+反映了人们存在损失决策权重高于获利决策权重的符号依赖效应。Schmidt和ZanK[7]构造指数τ=w-′(1-r)/w+′(r)=w-′(l)/w+′(r)，并指出：指数τ>1刻画了人们具有损失概率厌恶行为，系数τ越大，人们的损失概率厌恶程度越高。

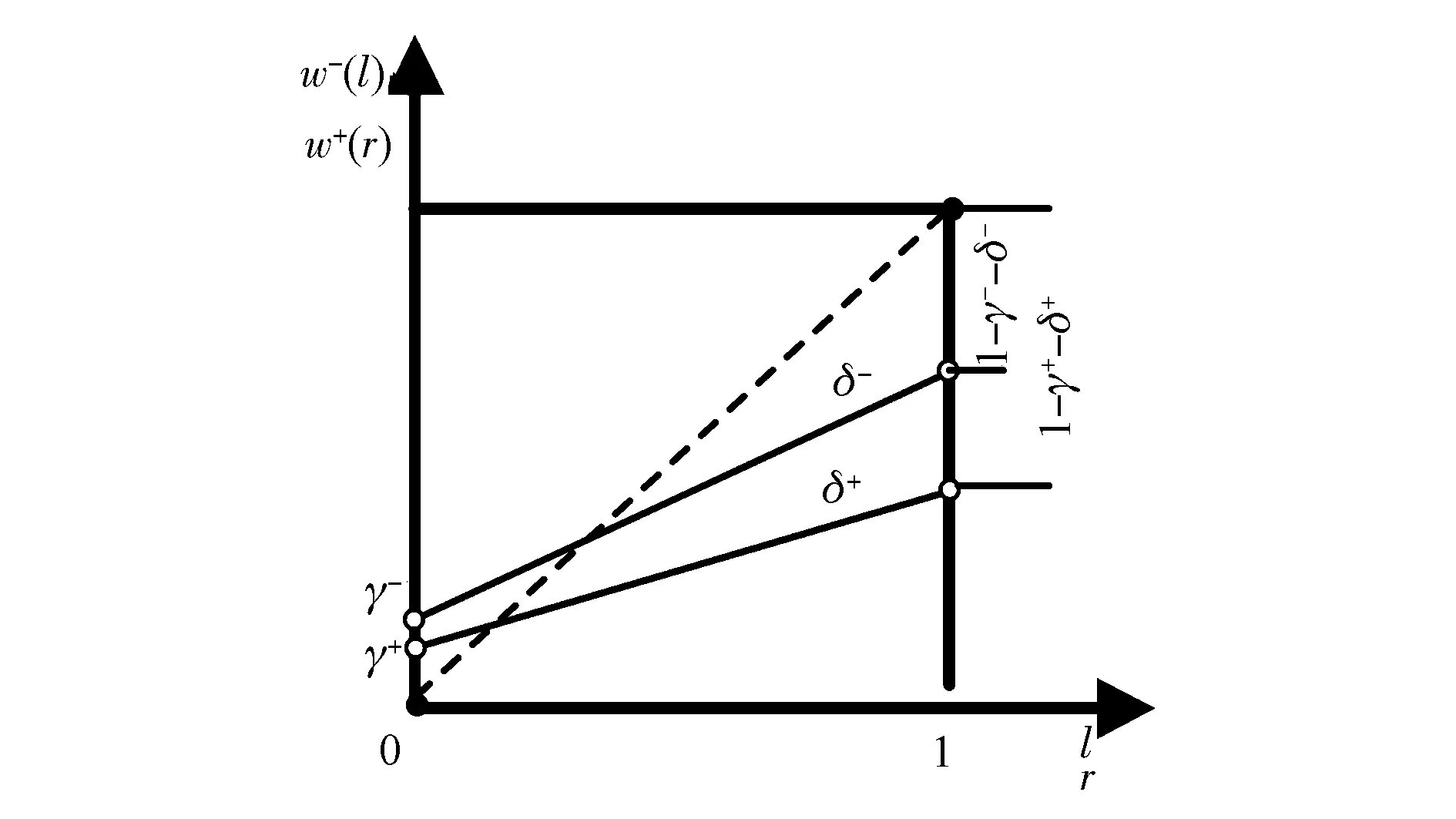
图1 权重函数

2.2随机利润和获利、损失排名

给定订购量Q，报童的随机利润：

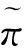
(1)

或

(2)

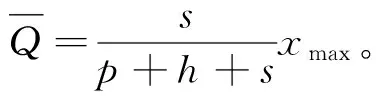
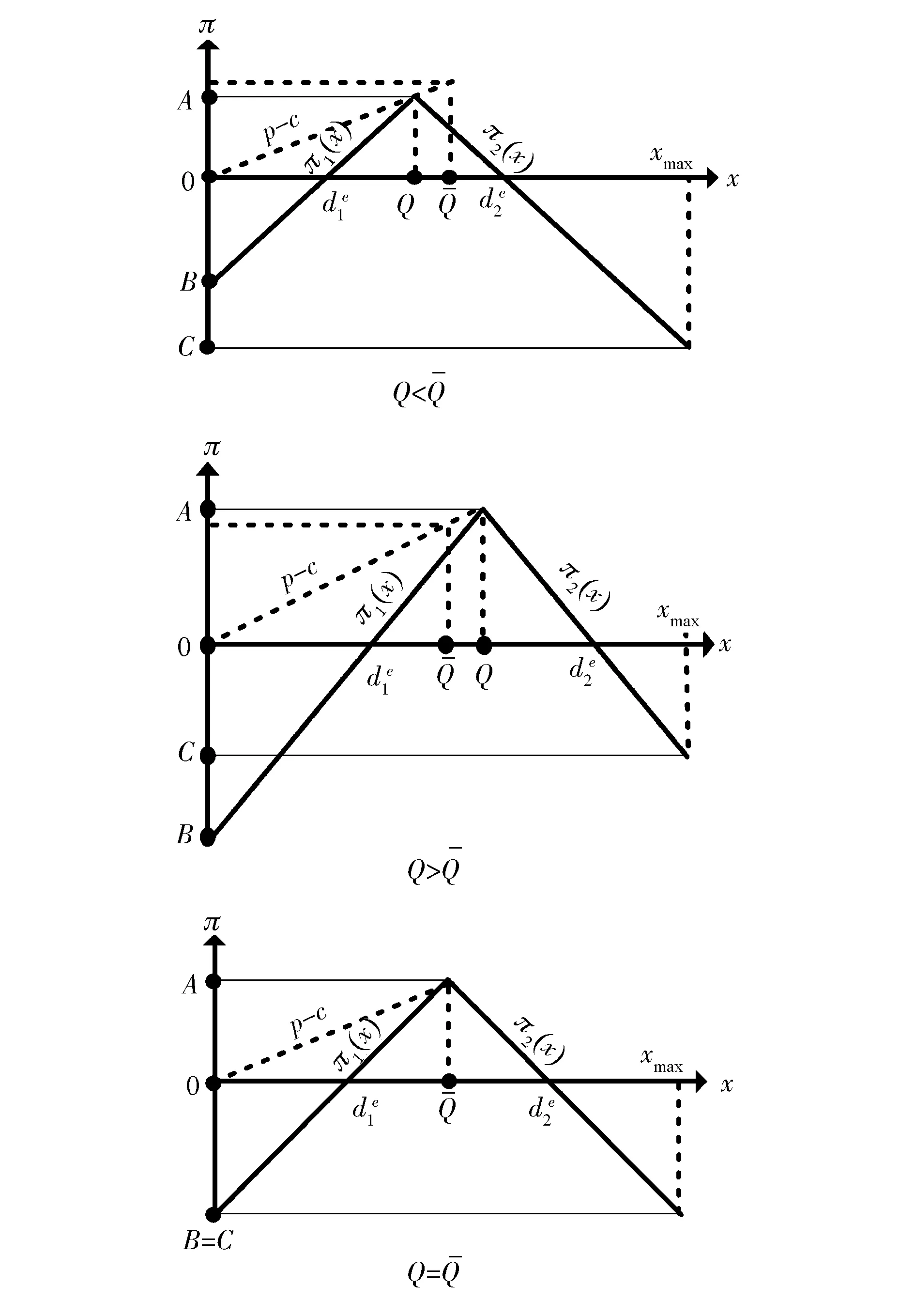
图2 利润π与需求x间的关系

记式(2)中利润函数π1(x)和x2(x)的反函数为：

(3)

式中，x1和x2分别为π1(x)和π2(x)的反函数。

由式(2)得盈亏平衡点：

(4)

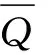
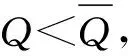
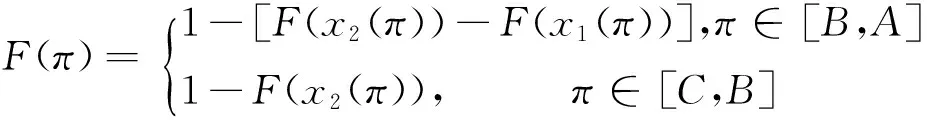
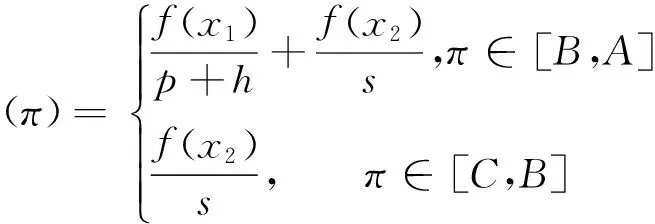
2)获利排名r、最大获利排名值rmax和损失排名l、最大损失排名值lmax分别为：

和

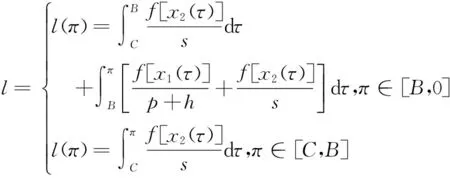
证明 1)关于累减分布函数G(π)，参见图2，由等价事件知：

因F(π)+G(π)=1，可得累进分布函数F(π)。因φ(π)=dF(π)/dπ，即：

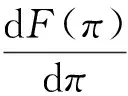
考虑式(3)，有dx1(π)/dπ=1/(p+h)、dx2(π)/dπ=-1/s代入上式得分布密度函数。

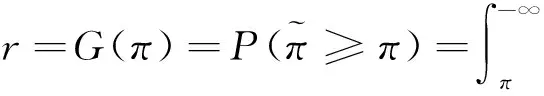
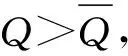
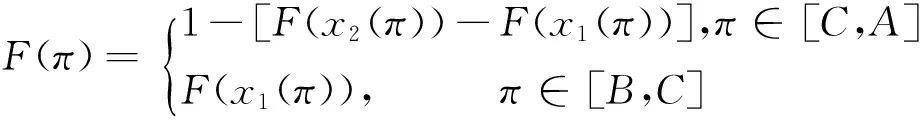
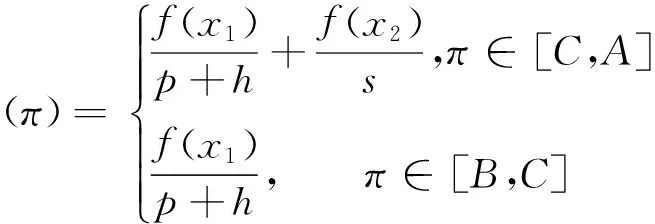
2)获利排名r、最大获利排名值rmax和损失排名l、最大损失排名值lmax分别为：

和

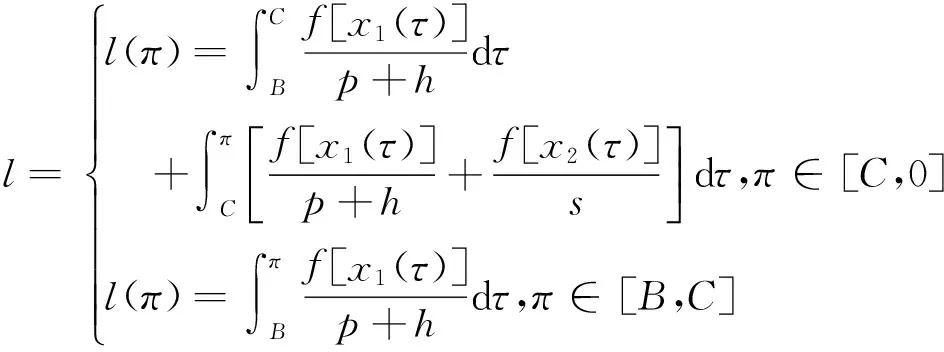
证明 1)首先证明累减分布函数G(π)。参见图2，由等价事件知：

利用F(π)+G(π)=1，得累进分布函数F(π)。因φ(π)=dF(π)/dπ，即：

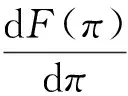
由式(3)知：dx1(π)/dπ=1/(p+h)、dx2(π)/dπ=-1/s，将其代入上式得分布密度函数。

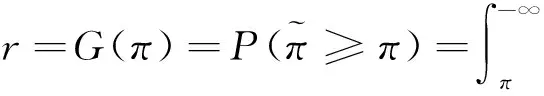
2.3利润前景值函数及其性质

基于累计前景理论[5]，给定订购量Q，随机利润的前景值：

(5)

定理1若报童为损失概率厌恶和损失厌恶者，即报童行为参数满足假设3和4，则其随机利润的前景值PT(Q)为：

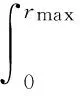
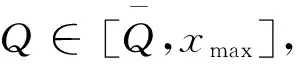
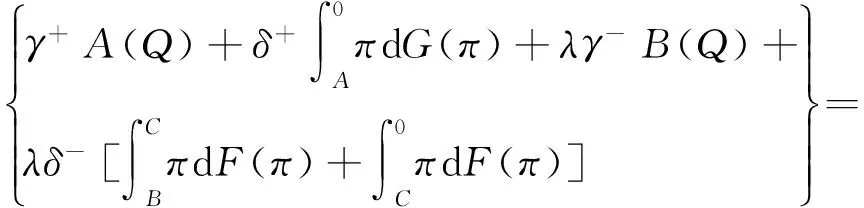
定理2前景值函数PT(Q)为区间[0,xmax]上的连续凹函数。

证明首先证明TP1(Q)函数为区间[0,Q]上的凹函数。对PT1(Q)微分，可得：

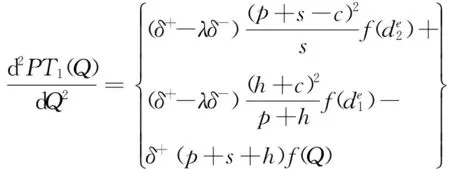
因报童是损失概率厌恶者(δ+<δ-)和损失厌恶者(λ≥1)，即δ+-λδ-<0，故d2PT1(Q)/dQ2<0。

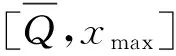
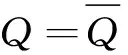
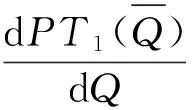
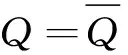
2.4订购量的确定和特殊情况分析

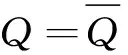
(6)

或更明确地表示为：

(7)

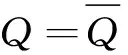
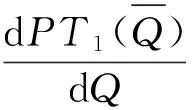
推论1若报童仅为损失厌恶者(λ≥1)，即其损失概率厌恶系数γ+=0、γ-=0、δ+=1、δ-=1，则其最优订购量满足：

F(Q*)=

推论2 若报童为风险中性者，即其损失厌恶系数λ=1,且其损失概率厌恶系数γ+=0、γ-=0、δ+=1、δ-=1,则其最优订购量满足：

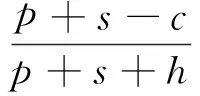
3 比较静态分析

本节揭示损失概率厌恶系数对订购量的影响。我们将内点最优性条件写成隐函数形式：

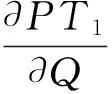
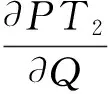
利用隐函数法则，可得如下比较静态结果。

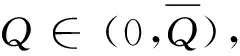
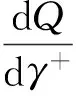
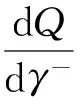
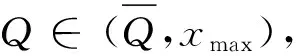
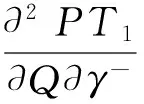
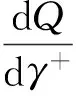
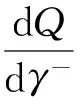
有关行为参数δ+，δ-，λ对最优订购量的影响，我们通过算例揭示。

4 数值算例

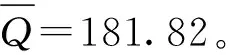
表1结果验证了定理4的结论：随极端获利结果重视程度的提高，最优订购量增加；随极端不利结果重视程度的提高，最优订购量减少。随缺货成本的增大，最优订购量增加。表2结果表明：随获利敏感度的提高，最优订购量增加，前景值增大；随损失敏感度的提高，最优订购量增加，但前景值减少；随损失厌恶系数的提高，最优订购量减少，前景值亦减少。

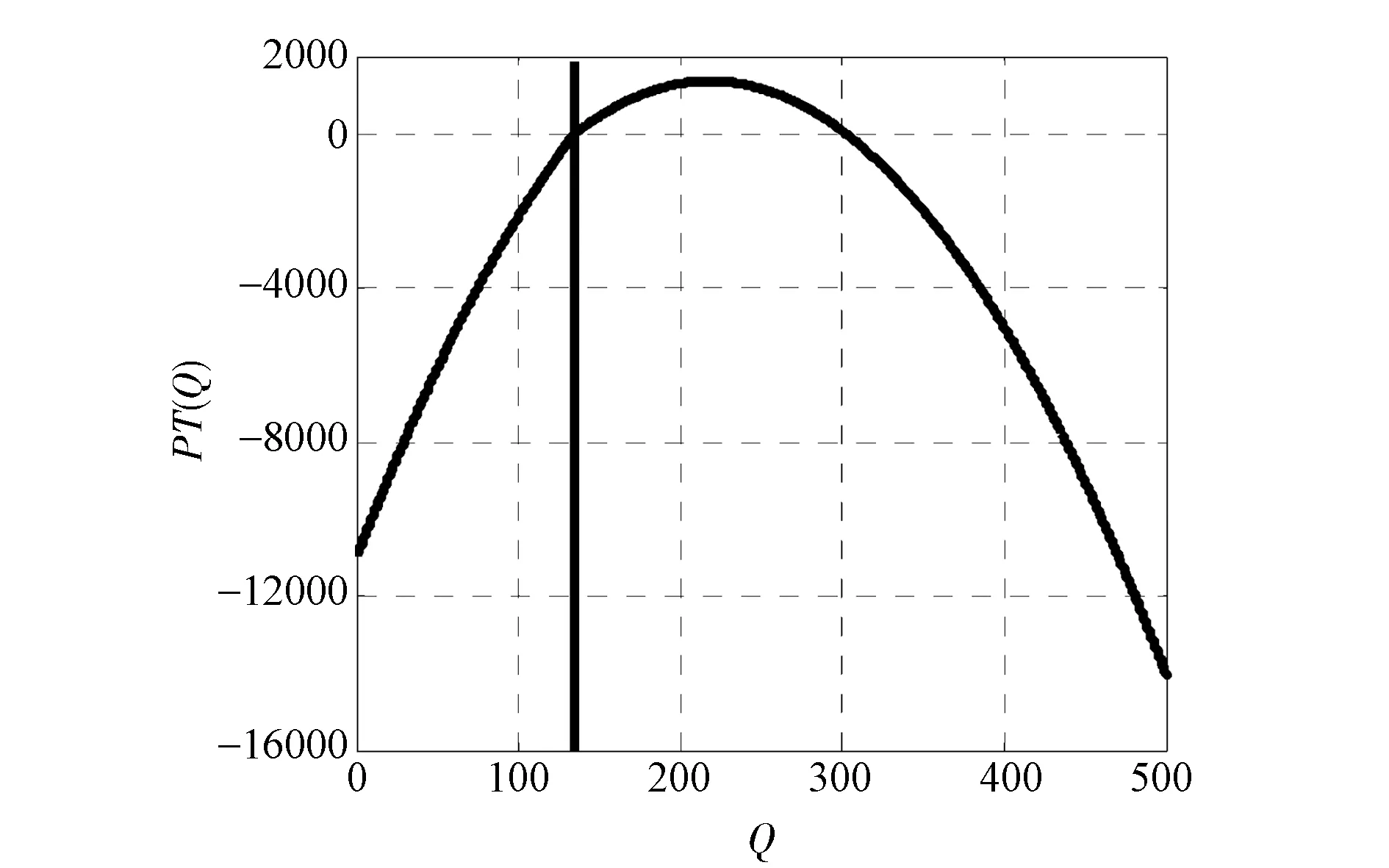
图3 前景值函数PT(Q)

5 结论

本文研究了具损失厌恶和损失概率厌恶的双重行为报童问题。通过定义最大损失等量订购量，分析了订购量小于和大于最大损失等量订购量时随机利润的分布及其随机获利和损失的排名，构建了其前景值函数，揭示了前景值函数为其订购量的连续凹函数但在最大损失等量订购量处不可微的性质，给出了仅具损失厌恶或风险中性的特例情况的结论，进行了极端结果行为参数的比较静态分析。结果表明：最优订购量小于最大损失等量订购量时，随极端获利和极端不利结果重视程度的提高，最优订购量增加；最优订购量大于最大损失等量订购量时，随极端获利结果重视程度的提高，最优订购量增加；随极端不利结果重视程度的提高，最优订购量减少。为了探讨非极端结果行为参数、损失厌恶参数以及缺货成本对订购量的影响，算例结果表明：随非极端获利和非极端损失结果敏感度的提高，最优订购量增加；随损失厌恶系数的提高，最优订购量减少。

表1 损失概率厌恶系数γ+、γ-以及缺货成本的比较静态分析

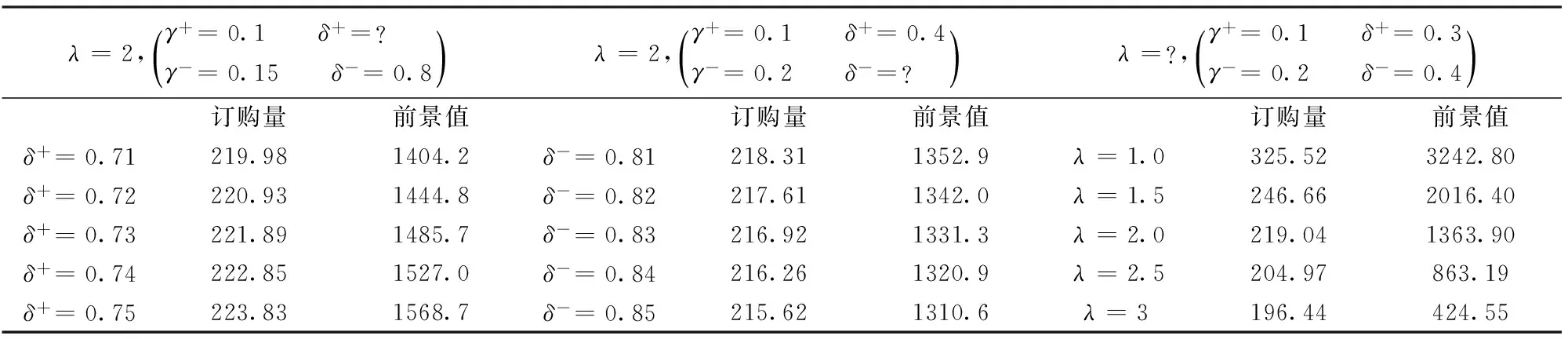
表2 损失概率厌恶系数δ+、δ-以及损失厌恶系数λ的比较静态分析

[1] 陈杰,唐萍,高腾.带有多元马氏需求的多产品报童模型[J].中国管理科学,2017,25(2):57-67.

[2] 张永,张卫国,徐维军.无统计信息假设下的多阶段报童决策[J].中国管理科学,2015,23(5):107-115.

[3] 陈杰,陈志祥,邢灵博,等.带有能力约束的多元马氏需求报童模型[J].管理科学学报,2016,(7):37-49.

[4] Loewensteiin G F,Weber E U,Hsee C K,et al.Risk as feelings[J].Psychological bulletin,2001,127(2): 267-286.

[5] Tversky A,Kahneman D.Advances in prospect theory: Cumulative representation of uncertainty[J].Journal of Risk and uncertainty,1992,5(4): 297-323.

[6] Quiggin J.A theory of anticipated utility[J].Journal of Economic Behavior &Organization,1982,3(4): 323-343.

[7] Schmidt U,Zank H.Risk aversion in cumulative prospect theory[J].Management Science,2008,54(1): 208-216.

[8] Schweitzer M E,Cachon G P.Decision bias in the newsvendor problem with a known demand distribution: Experimental evidence[J].Management Science,2000,46(3): 404-420.

[9] 文平.损失厌恶的报童-预期理论下的报童问题新解[J].中国管理科学,2005,13(6): 64-68.

[10] Wang C X,Webster S.The loss-averse newsvendor problem[J].Omega,2009,37(1): 93-105.

[11] Shen Houcai,Pang Zhan,Cheng T C E.The component procurement problem for the loss-averse manufacturer with spot purchase[J].International Journal of Production Economics,2011,132(1): 146-153.

[12] 周永务,肖旦,李绩才.损失规避零售商订货量与广告费用的联合决策[J].系统工程理论与实践,2012,32(8): 1727-1738.

[13] 柳键,邱国斌,黄健.面对损失厌恶顾客的零售商订货定价策略及激励问题[J].控制与决策,2014,29(1): 107-112.

[14] Baron O,Hu Ming,Najafi-Asadolahi S,et al.Newsvendor selling to loss-averse consumers with stochastic reference points[J].Manufacturing &Service Operations Management,2015,17(4):456-469.

[15] 张鹏,张杰,马俊.两种需求情形下损失规避零售商的最优订货-定价联合决策[J].控制与决策,2015,30(10)：820-827.

[16] 周艳菊,应仁仁,陈晓红,等.基于前景理论的两产品报童的订货模型[J].管理科学学报,2013,16(11): 17-29.

[17] Geng Wei,Zhao Xiaobo,Gao Deng.A single-period inventory system with a general S-shaped utility and exponential demand[J].Journal of Systems Science and Systems Engineering,2010,19(2): 227-236.

[18] 刘咏梅,成尚汶,谢虎.具有损失厌恶偏好零售商的供应链弹性数量契约[J].控制与决策,2012,27(7): 975-982.

[19] 胡劲松,赵光丽.具有损失规避零售商的模糊供应链网络均衡[J].控制与决策,2014,(10):1899-1906.

[20] 胡劲松,朱太硕,王永波.损失概率厌恶和损失厌恶行为零售商的供应链网络均衡[J].控制与决策,2016,31(7):1296-1304.

Abstract： It is found that the newsboy has loss of disgust and loss of probability aversion characteristics.In the paper,the Newsboy model with loss aversion and probabilistic loss aversion under shortage cost is studied.Using stochastic profit distribution functions and ranking functions when order quantity is less than maximum loss equivalent and order quantity is greater than maximum loss equivalent,its prospect value function is derived,and the nature of prospect value is revealed.The results show that the prospect value function is a continuous and non differentiable convex function,in which non differentiable points is in maximum loss equivalent;and Newsboy models with loss aversion or risk neutral are its special case.The analysis shows that: under the optimal order quantity being less than the maximum loss equivalent,the optimal order quantity increases with the increase of the degree on the extreme gain and unfavorable results.Under the optimal order quantity being greater than the maximum loss equivalent,the optimal order quantity increases with the increase of the degree on the extreme gain,and the optimal order quantity reduces with the degree on the extreme unfavorable results.The numerical results show that the optimal order quantity increases with the increase of the sensitivity of non extreme gain and non extreme loss.With the increase of the loss aversion coefficient,the optimal order quantity decreases.This study is helpful to understand the impact of the behavioral characteristics of newsboy on decision making.

Keywords： newsvendor problem；prospect theory；loss aversion;probability loss aversion

Newsboy Problem with Probabilistic Loss Aversion and Loss Aversion

MADe-qing1,HUJin-song1,JIANGWei2,CHENLiang1

(1.School of Business,Qingdao University,Qingdao 266071,China；2.School of Economics,Qingdao University,Qingdao 266071,China)

F274

A

1003-207(2017)09-0188-09

10.16381/j.cnki.issn1003-207x.2017.09.021

2016-11-23；

2017-02-26

国家自然科学基金资助项目(71371102);国际(地区)合作与交流项目(71311120090)

胡劲松(1966-)，男(汉族)，湖北京山人，青岛大学商学院教授，研究方向：行为运营、行为博弈，E-mail:hujinsong@qdu.edu.cn.