基于双指数跳跃扩散模型的长寿债券定价研究
2017-10-13邹辉文
巢 文,邹辉文
(1.福州大学经济与管理学院,福建 福州 350116;2.福州大学投资与风险管理研究所,福建 福州 350116)
基于双指数跳跃扩散模型的长寿债券定价研究
巢 文1,邹辉文2
(1.福州大学经济与管理学院,福建 福州 350116;2.福州大学投资与风险管理研究所,福建 福州 350116)
伴随着人均寿命的延长,人口老龄化带来的长寿风险问题成为世界各国必须面对的重要课题。长寿风险对各国的社保部门、寿险公司和政府造成了严重影响,如何有效地管理长寿风险成为学术界研究的焦点。鉴于已有长寿债券研究模型在考虑人口死亡率正负向不对称跳跃方面的不足,本文在Lee-Carter模型的基础上,采用双指数跳跃扩散模型对死亡率的正负向不对称跳跃进行刻画,并运用经典的CIR利率模型对长寿债券进行贴现,然后通过引入风险中性定价法给出不完全市场中的债券定价,使得定价更贴近真实市场。对人口死亡数据进行实证分析的结果表明,本文模型度量长寿风险的能力要明显优于已有模型。因此,应用本文模型进行债券定价,不仅可以提供更合理的定价,还可以提高寿险公司应对长寿风险的能力,从而促进寿险业在我国的进一步发展。
长寿债券;CIR利率模型;双指数跳跃扩散模型;风险中性
1 引言
随着社会的进步,医疗卫生条件和经济生活水平的改善,人类的死亡状况不断好转,寿命呈现不断延长的趋势。长寿风险使得各国的寿险业、养老机构等的金融压力变大,面临严重的支付危机,其造成的社会影响已经引起各国的广泛关注。传统的风险管理方法很难实现长寿风险的转移,需从新型的金融衍生工具中寻找出路。而长寿债券是一种有效管理风险的方法,它通过债券交易方式,将寿险公司承保的长寿风险传递给资本市场的广大投资者。它的出现,既可以对冲长寿风险,又能活跃资本市场。
长寿风险对社会各领域带来严峻挑战,如何对冲该风险引起学术界的关注。如曾燕等[1]在长寿风险对冲框架下,通过引入外生的产品价格,构建了基于价格调整的自然对冲模型;汪伟和刘玉飞[2]探讨农民工进城对养老保险体系的养老账户缴费、养老基金给付等方面的短期和长期影响,最后给出了政府应承担农民工长寿风险,在财政上做好兜底工作等政策启示。另外,国内外有许多的研究者从长寿债券角度对长寿风险进行了研究,主要从死亡率预测研究、长寿债券的定价研究以及长寿证券衍生品的研究。Cairns等[3]认为,一个好的死亡率模型需要能够使预测结果与未来实际结果相吻合。为改善以前模型对死亡随机性刻画的不足,Wills和Sherris[4]用实证方法表明:死亡率的相关效应对长寿债券定价的影响较大。Wang和Yang[5]在传统Lee-Carter的基础上,用中国人口死亡数据进行同年出生死亡率相关性的拓展研究。然而在研究寿险产品定价时,只有不多的研究会强调死亡率的跳跃性。尚勤等[6]考虑到中国人口老龄化具有基数大、速度快的特点,运用OU跳随机过程刻画死亡强度。Bauer等[7]研究长寿债券时,在连续时间框架下,利用仿射跳跃扩散模型刻画死亡率。Cox等[8]提出了同时描述长寿跳跃和死亡跳跃的模型。Deng等[9]基于双指数跳跃扩散模型采用风险中性定价方法对寿险产品进行定价研究。田梦和邓颖璐[10]采用双指数跳跃扩散模型,对中国人口死亡率进行预测,并得到了寿险衍生品q远期的中国定价。从已有研究来看,目前还未看到将双指数跳跃扩散模型应用到长寿债券定价中的成果。
长寿债券合理定价受死亡率的刻画和利率期限结构的影响,但很多的研究者仅将注意力集中于死亡率的预测,对利率风险重视不够。本文在前人研究的基础上,考虑到死亡强度正负向跳跃的不对称性,采用双指数跳跃扩散模型刻画死亡强度。同时考虑利率期限结构和市场的不完全性,用CIR利率模型描述利率,然后通过风险中性定价给出长寿债券的价格。最后,进行参数敏感度分析,找到影响债券价格的主要因素。
2 长寿债券的构造原理
长寿债券是传统保险业和证券行业结合的产物,它通过债券交易方式,将本该由寿险公司承担的长寿风险,转移到资本市场。SPV是寿险公司和投资者的交易中介,它向寿险公司购买再保险,再向投资者发售无违约债券。在交易期内,当生存指数高于双方约定的程度时,SPV用发行债券的收益优先向寿险公司赔付,剩余资金再向投资者发放息票,生存指数决定了各方的收益和风险。因此,准确预测死亡强度是长寿债券合理定价的关键。此外,由于长寿债券期限较长,一般为25年或者30年,它的价值受利率波动影响较大,在给其定价时,利率期限结构不可忽视。长寿风险的产生和分散过程图如图1所示。
图1中,寿险公司用固定年金的方式向SPV支付再保险费,SPV再以浮动年金的形式赔付给保险公司。同时,对于投资者来说,他们向SPV支付固定的息票债券,得到浮动的息票债券。SPV和投资者都承担了风险,好处是得到了较高风险的报酬。明显的,死亡率的预测是长寿风险管理的关键。
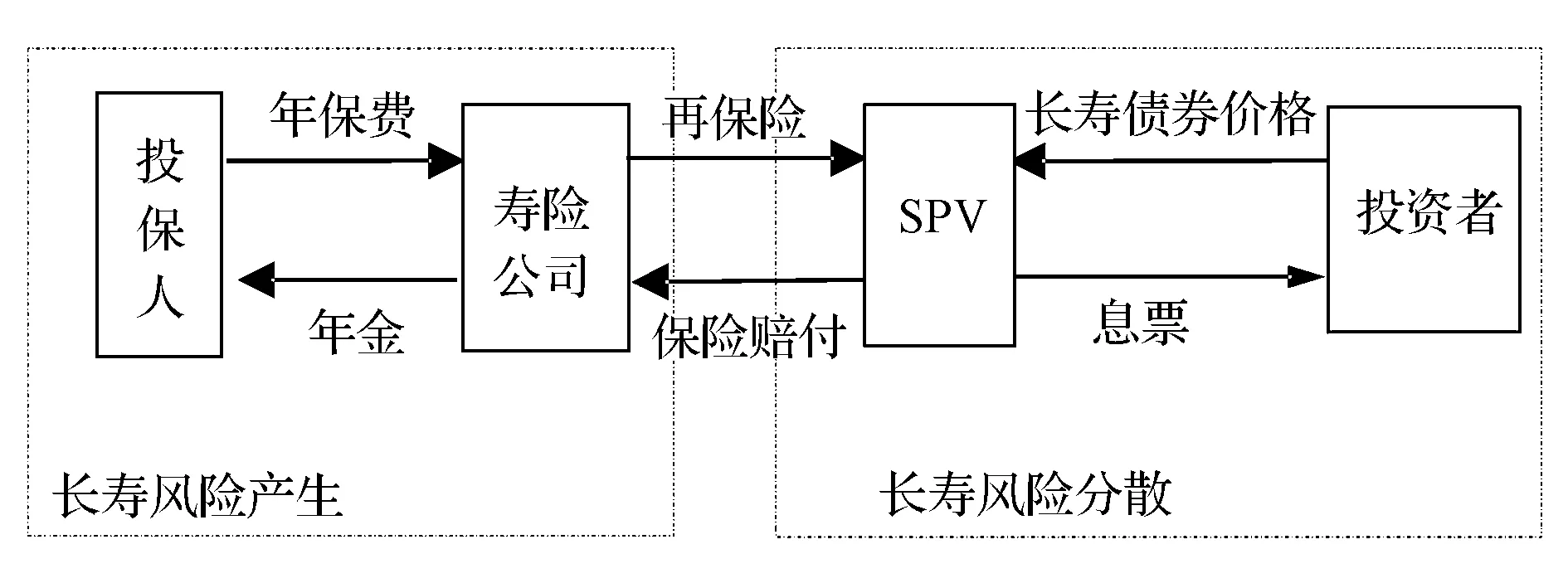
图1 长寿风险产生和分散过程图
3 DEJD模型下的死亡强度
研究长寿债券定价,首先要刻画生存指数,而生存指数需要通过计算死亡强度得到。本文考虑死亡强度具有正负向跳跃的不对称性,同时又兼顾良好的运算性质,将采用双指数跳跃扩散模型(DEJD模型)来刻画死亡率。模型的基本结构为:
(1)
式中kt是整体死亡率,又叫时间序列因子;Wt为标准布朗运动;N(t)是带跳的泊松过程(跳跃频率是λ),α和σ分别表示瞬时期望漂移率和波动率;Vi是服从独立同分布的非负随机变量。若令Y=ln(V),则Y服从不对称的双指数分布,其密度函数为:
fy(y)=pη1e-η1y1{y≥0}+qη2eη2y1{y<0},η1,η2>0,p,q≥0,p+q=1,
(2)
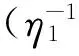
根据Kou 和 Wang Hui[11],一个风险中性的DEJD模型结构如下,其中带*号表示表示各参数经过风险中性调整:
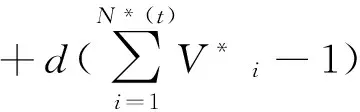
(3)
且
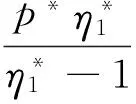
(4)
整理得到第t年x年龄组的死亡率mx*(t)[9]:
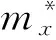
(5)
其中,ax为各年龄组死亡率自然对数的平均水平,bx表示各年龄组死亡率对数变化的偏差情况。
4 长寿债券定价模型
4.1债券设计
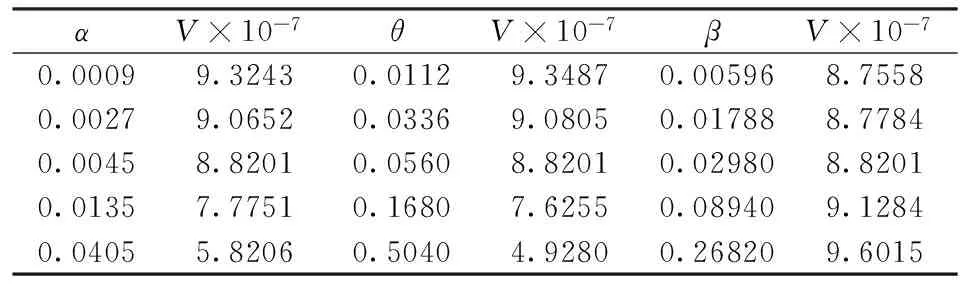
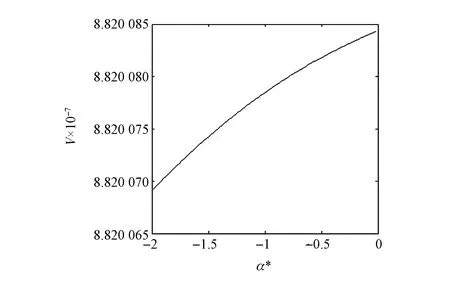
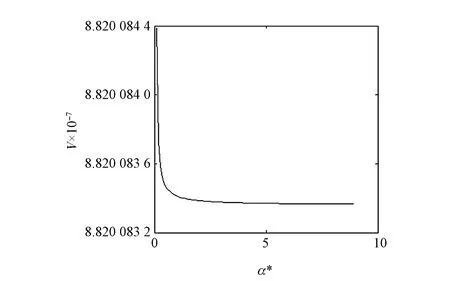
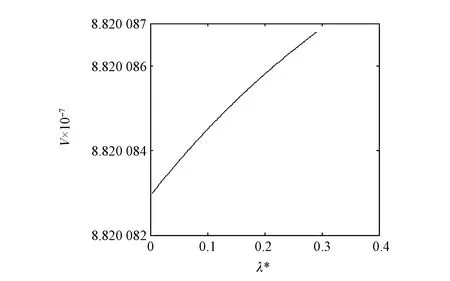
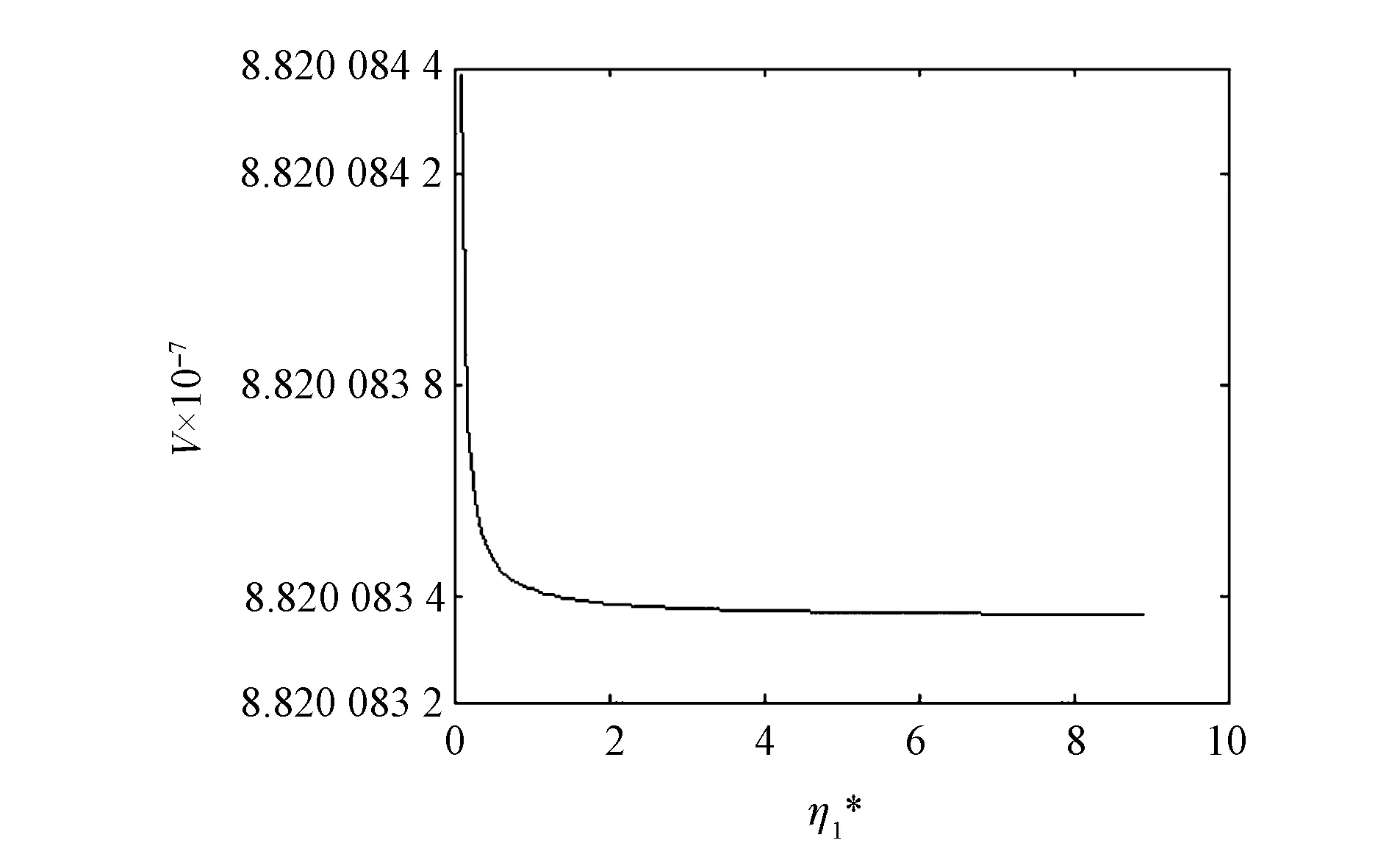
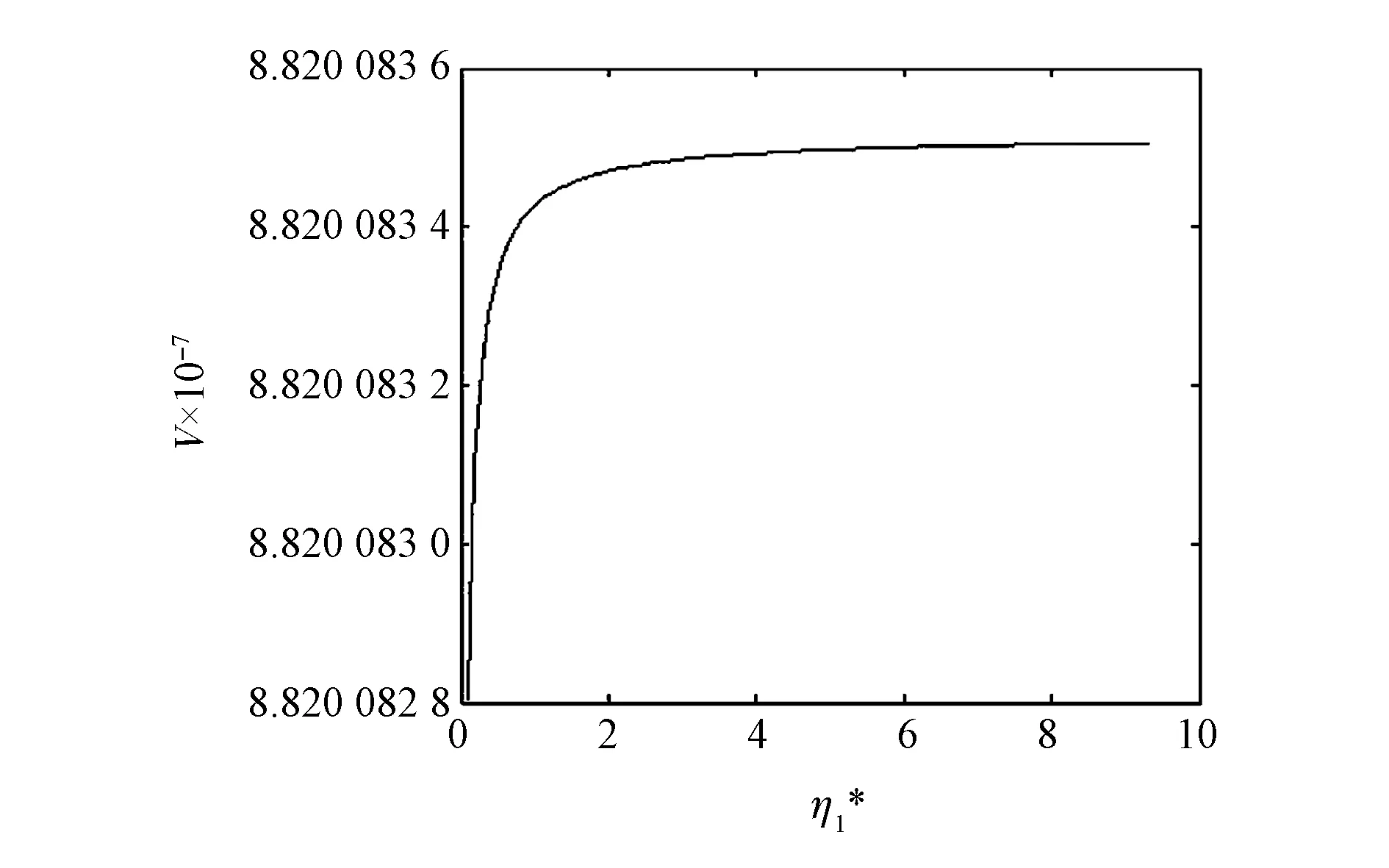
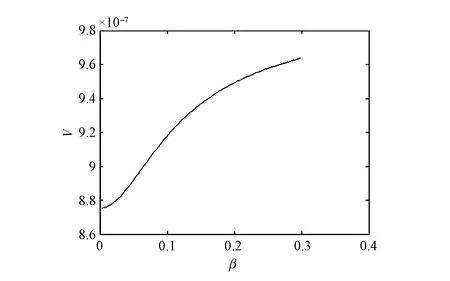
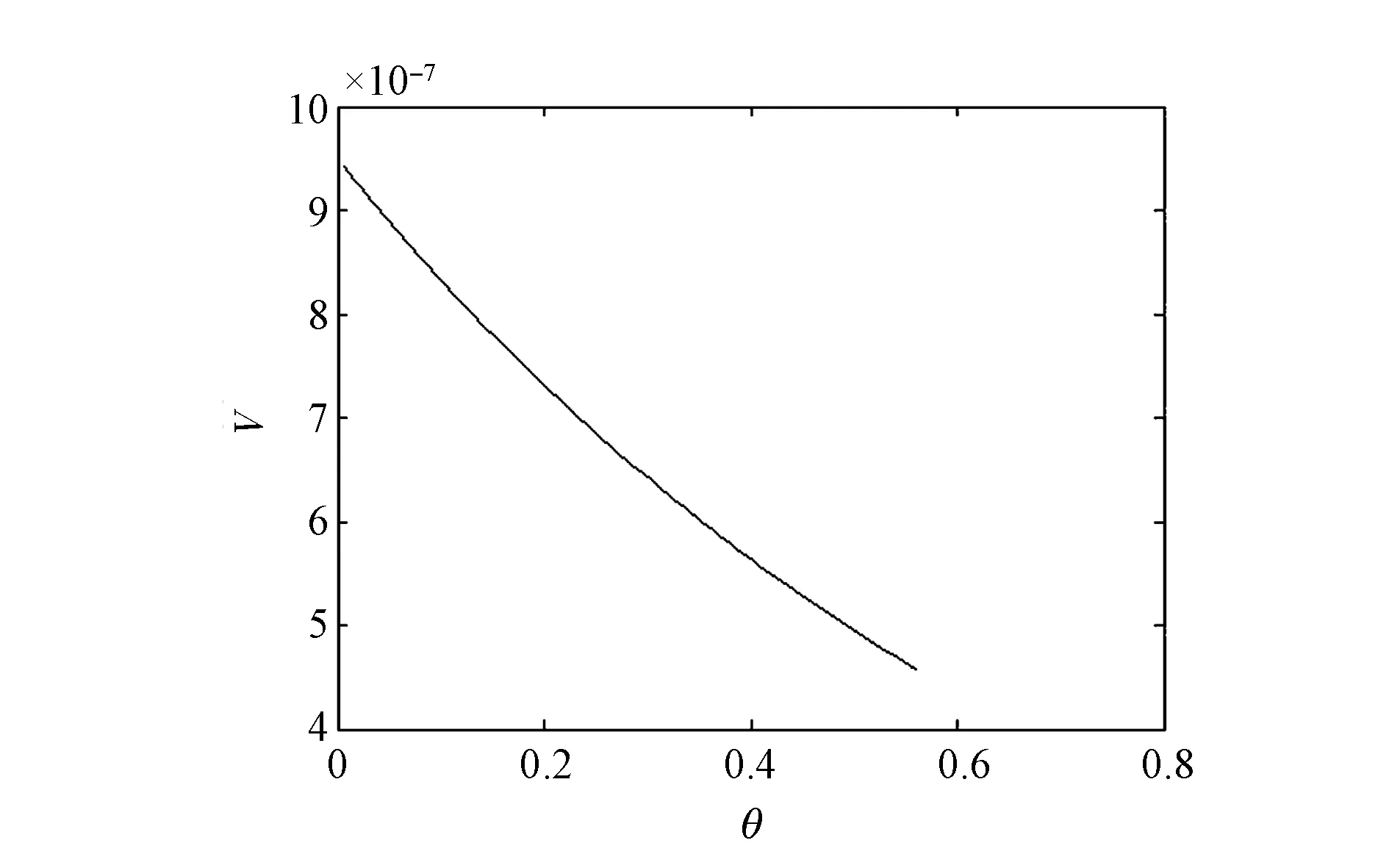
假设lx表示x岁的人数,lx+t表示lx个x岁的人活到x+t岁的人数(lx+t (6) 令V为长寿债券价格,T年期的面值为F,SPV支付给投资者的息票是Dt,V和Dt的关系满足: (7) 其中,d(0,t)是基于无风险利率r(t)下的折现因子, (8) 4.2利率期限结构 在过去的30年中,经济学家提出了大量的利率模型,大致可以分为单因子和多因子利率。单因子利率变量少,具有易处理和参数易估计的优势。在长寿债券的研究中,我们注重的是对死亡率随机特征的刻画和定价模型的可操作性,因此,选择单因子利率模型。基本的单因子利率模型有Merton模型,Vasicek模型和Cox-Ingersoll-Ross模型。Merton模型不能描述利率均值回复和保证利率恒正,而Vasicek模型虽有均值回复项,但不能保证利率恒正,只有CIR模型才能同时体现这些特征。因此,本文采用CIR模型来描述利率的波动形态: (9) 式中,α、β和θ为参数;W(t)为标准布朗运动。 根据Cox,Ingersoll和Ross[12]的相关结论,在CIR模型下零息债券的风险中性价格p(0,t)可写成如下形式: (10) 要求债券价值V的值,关键是求E*(Dt),其中带*表示参数经过风险中性调整,由(6)式可得: Dt=lb-(lx+t-lat,0)++(lx+t-lat-lb,0)+ 则:E*(Dt)=lb-E*[(lx+t-lat)+]+E*[(lx+t-lat-lb)+] (11) (12) (13) (14) 根据φ′(t)=-tφ(t),由分部积分 (15) 可得: (16) (17) 将(16)(17)两式代入式(11),得到 (18) (19) 5.1参数估计 5.1.1 参数ax和bx估计 本文采用美国国家健康统计中心提供的1900-2004年的死亡率数据,并应用矩阵奇异值分解法(SVD法)进行ax和bx的估值。首先,进行正态化假设: mx,t=exp(ax+bxkt+εx,t) (20) 仿真结果表明,在2~4 GHz的频带范围内,低噪声放大器的输入回波损耗小于-8 dB,输出回波损耗小于-10 dB。频率为2 GHz时,增益取得最小值为30.6 dB,频率为3.15 GHz时,增益取得最大值为31.9 dB,增益的平坦度小于等于1.3 dB。噪声系数的最小值为0.75 dB,此时频率为3 GHz。噪声系数的最大值为1 dB,此时的频率为2 GHz,即在工作频带内,噪声系数的取值不大于1 dB。根据前面的分析可知,稳定系数μ大于1时,低噪声放大器处于绝对稳定的工作状态,通过仿真的结果可知,在整个频带范围内,稳定系数大于2.6,因此保证放大器不会被自激等不理想因素所影响。 上述的计算过程可用Matlab软件编程实现,结果见表1。 表1 年龄效应参数回归结果 5.1.2 DEJD模型参数估计 用C={k0,k1,…,kT}表示死亡率时间序列,并记一个时期的增量ri=Δki=ki-ki-1(i=1,2,…,T),则ri的无条件密度函数f(r)为: f0,0(r),f0,n(r)和fm,n(r)计算过程类似,这里不再给出。下一步,由ri的独立性可得对数似然函数为: 其中λ=λ1+λ2,p=λ1/λ。最后编程得到参数的极大似然估计值,结果见表2。 表2 死亡率其他参数估计值 5.1.3 CIR利率模型参数估计 通过选取2008-12-31~2012-12-31的1年期Shibor数据,估计CIR利率模型中的参数。利用极大似然估计法估计式(9)中的参数[13],α=0.0045,β=0.0298,θ=0.056。 5.2定价示例 下面,将本文的计算结果与不同模型的定价方法给予比较分析,为长寿债券研究提供进一步参考。如表3。 表3 不同模型刻画死亡率方法的结果比较 由表3比较可知,由带跳的OU过程和Feller过程刻画死亡强度,得到的长寿债券价格要低于DEJD模型的结果,即不考虑死亡率正负向跳跃的情况下,长寿债券价格会被低估。这是因为,当考虑死亡率的正负向跳跃,且正向跳跃强度比负向跳跃强度更大(η1*<η2*)时,死亡率的正向跳跃会使投资者有更大收益,使其愿意为持有长寿债券支付更高的价格。若寿险公司不能有效的管理长寿风险,向投资人收取的债券价格低于“公平”价格,将导致寿险公司不堪重负,甚至破产。因此,准确预测人口死亡率,从而制定合理的债券价格,是寿险公司稳定经营的关键所在。 表4 DEJD模型中参数敏感度测试表 5.3参数敏感度分析 参数敏感度分析有助于在长寿债券定价时,根据具体情况调整参数。首先,分析死亡率模型的参数敏感度。 同样,对CIR利率模型中参数进行敏感度测试,如表5。参考表5中数据,设定每个参数的取值范围,取不同的值并绘图,得到图7-9。综合表5和图7-9,可以看出,若保持其他参数不变,随着参数α和θ的增大,长寿债券价格而变小;而当β增大时,长寿债券的价格也增大。其中,参数α的敏感度最显著,其他两个敏感度较弱。可见,对于期限较长的长寿债券而言,期限结构对长寿债券的价格具有密切的影响。因此,利率模型的选取和参数的估计十分重要,不容忽视。长寿债券作为一种新兴的金融衍生品,其到期期限一般较长,因此相较于短期利率的影响,长寿债券的定价模型更应重视远期利率的影响。 表5 CIR利率模型中参数及参数敏感度测试 图2 参数α*与V的关系 图3 参数σ*与V的关系 图4 参数λ*与V的关系 图5 参数与V的关系 图6 参数与V的关系 图7 参数α与V的关系 图8 参数β与V的关系 图9 参数θ与V的关系 随着全球人口老龄化社会的迅速形成,导致领取养老金保险金的人数逐年增加,而纳税人口一路减少,养老金账户的供需缺口越来越大,以致于影响了社会的发展。长寿问题已经成为不容忽视的重大社会问题,发行长寿债券,不仅可以减缓社会保障部门的金融压力,还可以为寿险业对冲长寿风险提供新思路。 本文在Lee-Carter模型的基础上,利用双指数跳跃扩散模型来刻画死亡率正向和负向跳跃的不对称性,从而更准确的度量长寿风险。并且在处理年龄别的参数时,利用线性插值法,既提高了死亡率预测的精度,又避免了多而繁琐的统计工作量。此外,用经典的CIR利率模型进行贴现,从示例和数据分析结果可以得出,增加利率期限结构是有必要的,而且对长寿债券的合理定价也有较大影响。 随着我国资本市场的发展,精算技术的不断成熟,人口数据的不断完善和规范,长寿债券的设计会更加符合实际,长寿债券也势必将在管理长寿风险中发挥重要作用,因此本文的研究具有重要的现实意义。 [1] 曾燕,曾庆邹,康志林.基于价格调整的长寿风险自然对冲策略[J].中国管理科学,2015,23(12):11-19. [2] 汪伟,刘玉飞.城镇化进程中农民工融入城乡养老保险体系研究[J].中国行政管理,2016,(6):87-93. [3] Cairns A J G,Blake D,Dowd K.Pricing death: Frameworks for the valuation and securitization of mortality risk[J].ASTIN Bulletin: The Journal of the IAA,2006,36(1):79-120. [4] Wills S,Sherris M.Securitization,structuring and pricing of longevity risk[J].Insurance Mathematics &Economics,2010,46(1):173-185. [5] Wang C W,Yang S S.Pricing survivor derivatives with cohort mortality dependence under the Lee-Carter framework[J].Journal of Risk and Insurance,2013,80(4):1027-1056. [6] 尚勤,秦学志,周颖颖.死亡强度服从Ornstein-Uhlenbeck 跳过程的长寿债券定价模型[J].系统管理学报,2008,17(3): 297-302. [7] Bauer D,Börger M,Russ J.On the pricing of longevity-linked securities[J].Insurance Mathematics &Economics,2010,46(1):139-149. [8] Cox S H,Lin Yijia,Pedersen H.Mortality risk modeling: Applications to insurance securitization[J].Insurance Mathematics &Economics,2010,46(1):242-253. [9] Deng Yinglu,Brockett P L,MacMinn R D.Longevity/Mortality risk modeling and securities pricing[J].Journal of Risk and Insurance,2012,79(3): 697-721. [10] 田梦,邓颖璐.我国随机死亡率的长寿风险建模和衍生品定价[J].保险研究,2013,(1): 14-26. [11] Kou S G,Wang Hui.Option pricing under a double exponential jump diffusion model[J].Management Science,2004,50(9): 1178-1192. [12] Cox J,Ingersoll J,Ross S.A theory of the term-structure of interest rates[J].Econometrica,1985,53(2):385-408. [13] 尚勤,张国忠,胡友群,等.基于Cameron-Martin-Girsanov 理论的长寿债券定价模型[J].系统管理学报,2013,22(4): 472-477. [14] 尚勤.死亡率关联债券的定价模型与实证研究[D].大连:大连理工大学,2009. [15] Shang Qin,Qin Xuezhi .Securitization of longevity risk in pension annuities[C]//Proceedings of the 2008 International Conference on Wireless Communications,Networking and Mobile Computing,Dalian,Qctober 12-14,2008. Abstract: With the extension of life expectancy,the countries in the whole world must face the fact that aging population brings longevity risk.Longevity risk has put severe impacts on security departments,insurance companies and the governments in the world.Therefore how to manage it effectively has become the focus of study by the academic society.In view of the fact that the research model of longevity bonds has not considered the positive and negative asymmetry jump of population mortality,and in order to hedge the risk of longevity,based on Lee-Carter framework,a double exponential jump diffusion model is introduced to measure the positive and negative asymmetry jump of mortality rates,the interest rate is described with CIR.And in order to make the pricing of bonds closer to the real market,the risk neutral pricing is used to price the bond in the incomplete market.Empirical analysis with the population death data shows that the ability of this model is significantly better than the existing model when measuring longevity risk.Therefore,the use of this model for bond pricing,not only can provide a more reasonable pricing,but also can improve the life insurance companies to deal with the risk of longevity,then can promote the further development of life insurance industry in China. Keywords: longevity bonds;CIR model;double exponential jump diffusion model;neutral risk Pricing Longevity Bonds based on Double Exponential Jump Diffusion Model CHAOWen1,ZOUHui-wen2 (1.Institute of Investment and Risk Management,Fuzhou University,Fuzhou 350116,China;2.School of Economics and Management,Fuzhou University,Fuzhou 350116,China) F830.91 A 1003-207(2017)09-0046-07 10.16381/j.cnki.issn1003-207x.2017.09.006 2015-10-17; 2017-02-25 福建省自然科学基金资助项目(2017J01794) 巢文(1988-),女(汉族),江西宜春人,福州大学经济与管理学院博士生,研究方向:金融资产定价,E-mail:chaowen2014@163.com.

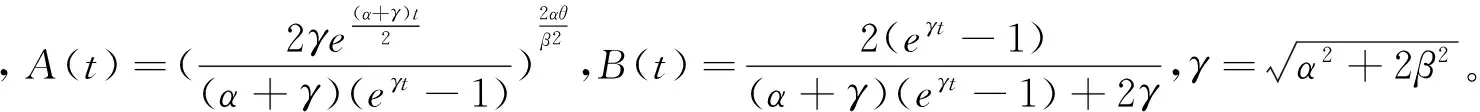
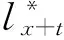
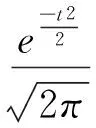

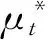
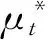
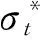
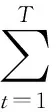
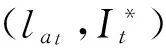
5 实证研究
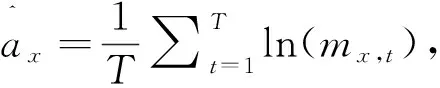
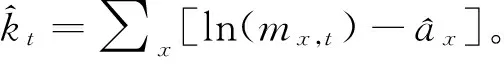
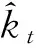
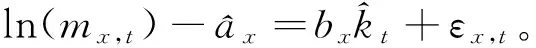

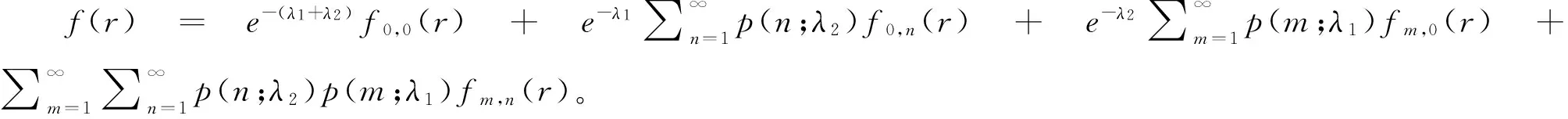
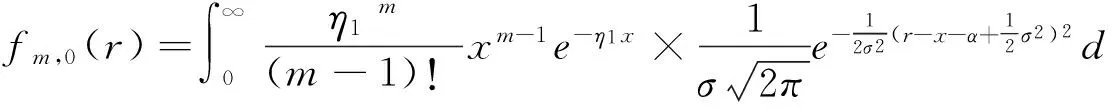
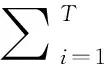

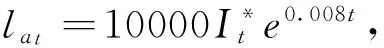
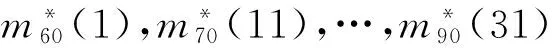


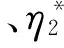

6 结语
