投资组合约束下分离交易可转债的定价
2017-10-13胡昌生程志富熊德超
胡昌生,程志富,陈 晶,熊德超,3
(1.武汉大学经济与管理学院, 湖北 武汉 430072;2.交通银行甘肃省分行, 甘肃 兰州 7300703.长江证券资金营运部, 湖北 武汉 430015)
投资组合约束下分离交易可转债的定价
胡昌生1,程志富1,陈 晶2,熊德超1,3
(1.武汉大学经济与管理学院, 湖北 武汉 430072;2.交通银行甘肃省分行, 甘肃 兰州 7300703.长江证券资金营运部, 湖北 武汉 430015)
分离债是近十年来在投融资领域中的创新金融工具之一,本文试图从结构化模型角度对这一产品进行定价。通过引入市场限制条件并加以刻画,建立新的分离债定价模型。具体而言,先参照Tsiveriotis和Fernandes(1998)等的思路将分离债拆分为权证和债券两部分,再借鉴Karatzas和Kou(1996)和Karatzas和Shreve(2004)的方法分别推导两者在投资组合约束下的无套利价格上界和下界,进而得出分离债的无套利价格区间。由于投资组合约束在现实市场中普遍存在,因此建立这种结构化模型是具有实际意义的。该模型不仅能反映现实市场对投资组合的约束,还可以捕捉到公司杠杆的实时变化。
分离债;结构化模型;投资组合约束;期权价值状态
1 引言
分离债的全称是“认股权和债券分离交易的可转换公司债券”,它是一种附认股权证的公司债,可分离为债券和认股权证两部分[1-2],给予了上市公司一次发行两次融资的机会。自从2006年5月《上市公司证券发行管理办法》正式实施以来,分离债这一创新品种因其两次融资、发行便利、成本低等特点,不仅满足上市公司的融资需求,也符合金融市场的发展方向,因而受到上市公司的青睐,正成为大型上市公司后续融资的一种重要工具。
从定义来看,分离债属于可转债(下简称转债)的范畴。因此,无论是实务界还是理论界,基本上都是沿用转债的定价方法为分离债定价。而根据Constantinides[3],Philips[4],Ferris等[5],以及刘娥平等[6]的观点,分离债和转债至少在票面利率、债券期限、转股价(或转股比率)以及其他附属条款(赎回、回售、担保和转股价修正)等方面存在较为显著的差异。不仅如此,由于国内市场长期以来都存在着不同程度的投资组合约束(即投资者在投资产品上所面临的头寸限制),使得分离债和转债在价格形成机制上的差异进一步凸显。可见,要探讨分离债的价值特性,至少应该将其自身的条款设置(内因)与市场客观存在的投资组合约束(外因)这两方面因素结合起来进行分析。
从分离债自身的条款设置上来讲,它具有如下几个特点:第一,分离债的票面利率不仅低于同期银行定存利率,也普遍低于同类型转债的利率。说明其债券部分更接近于零息债特点,并且久期和凸度要高于同类型的转债,对利率和公司违约风险更为敏感。第二,不同于转债,分离债通常都没有设立赎回条款、转股价修正条款,而且其回售条款对投资者的保护程度不大,也形同虚设。可见分离债中的权证部分等同于该公司发行的一份普通股本认购权证。第三,大部分的分离债都不需要附加担保条件,因而其债券部分的价值更依赖于公司资产负债的状况。尽管分离债普遍都以最高的评级AAA 发行,但由于国内评级机构的水平参差不齐,评级机构对发行人具有一定的依赖性,评级不能对债券的信用水平做很好的说明。
再来考虑外部因素,即市场上客观存在的投资组合约束。由定义可知,分离债的实质相当于其权证部分和债券部分的简单加总,因此,可以分别从权证和债券的定价来考察投资组合约束对分离债市场价格造成的影响。
综合上述分析,我们对分离债价值模型进行重新构建。先来看权证部分,根据条款设置上的第二个特点,分离债的权证部分相当于股本认购权证,因此,市场对股票交易的约束(即买空约束)势必会对权证价值造成冲击。如市场对保证金、杠杆率以及持仓限额等方面的规定,显然会影响投资者在其组合中的股票头寸,而这些摩擦因素又可能进一步地导致权证市场价格偏离Black-Scholes[7]公式对应的期权价值(下简称BS价格)。再来看债券部分,结合条款设置上的第一点和第三点可知,分离债中债券部分的价值与其他公司债券价值本质上是一致的。Merton[8]最早在无约束的条件下对公司债券进行了结构化建模[9],而Huang Jingzhi和Huang Ming等[10]经验研究则发现结构化模型的估值会显著高于债券市价。有学者认为这可能是由于现实市场上存在的约束(即卖空约束)所导致的[10-12]。其逻辑是,如果模型是正确的,那么当市场价格低于理论价格时,投资者可通过买入公司债券同时卖空公司资产和无风险证券以获取无风险收益。然而,现实中上述策略的实施将面临卖空约束。一方面,公司资产不可交易,投资者得借助股票(相当于公司资产的看涨期权)等工具复制出公司资产再间接做空,不过该策略在股票这一期权处于深度虚值时将可能失效。另一方面,即使复制策略有效,市场对于股票的做空同样有所限制。因此,债券套保同样会面临投资组合上的约束,进而使得其价格低于由Merton模型得出的理论价值。
迄今为止,国内外关于转债的定价理论和经验研究已经取得了诸多成果,如Ingersoll[13]和Brennam和Schwartz[14]分析了赎回条款和转换策略等因素的影响,杨大楷等[15]则重点讨论了国内转债的定价及相关条款设计的问题。不过,鉴于转债与分离债的差异,上述理论和成果对于后者可能未必适用。而有关投资组合约束方面的研究,除了理论上的进展,如Kraft和Steffensen[16],Fahim和Huang[17]等,经验研究上也有了新的证据,徐枫等[18],发现卖空限制对于证券的设计与发行是不容忽视的市场力量,方立兵和曾勇[19]的结论则进一步证明了现实市场中的限制卖空不会因为融资融券的推出而消失,这与Hong和Stein[20]的关于美国股票市场上的卖空交易亦存在诸多约束的观点也是一致的。在此背景下,本文从分离债所独有的性质出发,并考虑投资组合约束(买空约束、卖空约束)所带来的冲击,为分离债设计出一个更为合理的定价模型。
2 定量建模
为便于分析,本文的模型将重点考虑现实市场对资产的约束,而忽略其对借贷的约束。其中,分离债的权证部分主要受到标的股票买空约束的影响,而债券部分则主要受到公司资产卖空约束的影响。
2.1买空约束对权证部分的影响
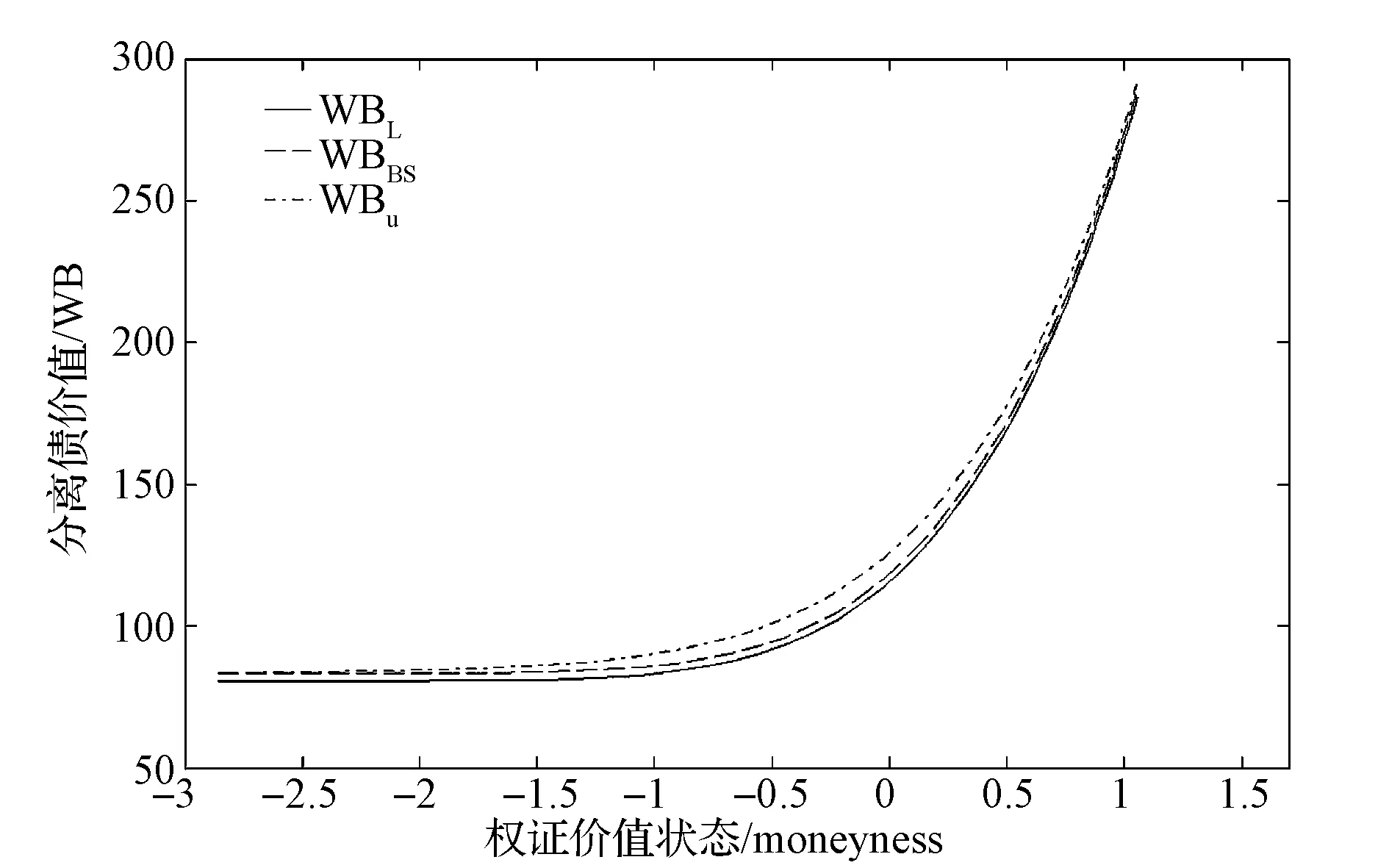
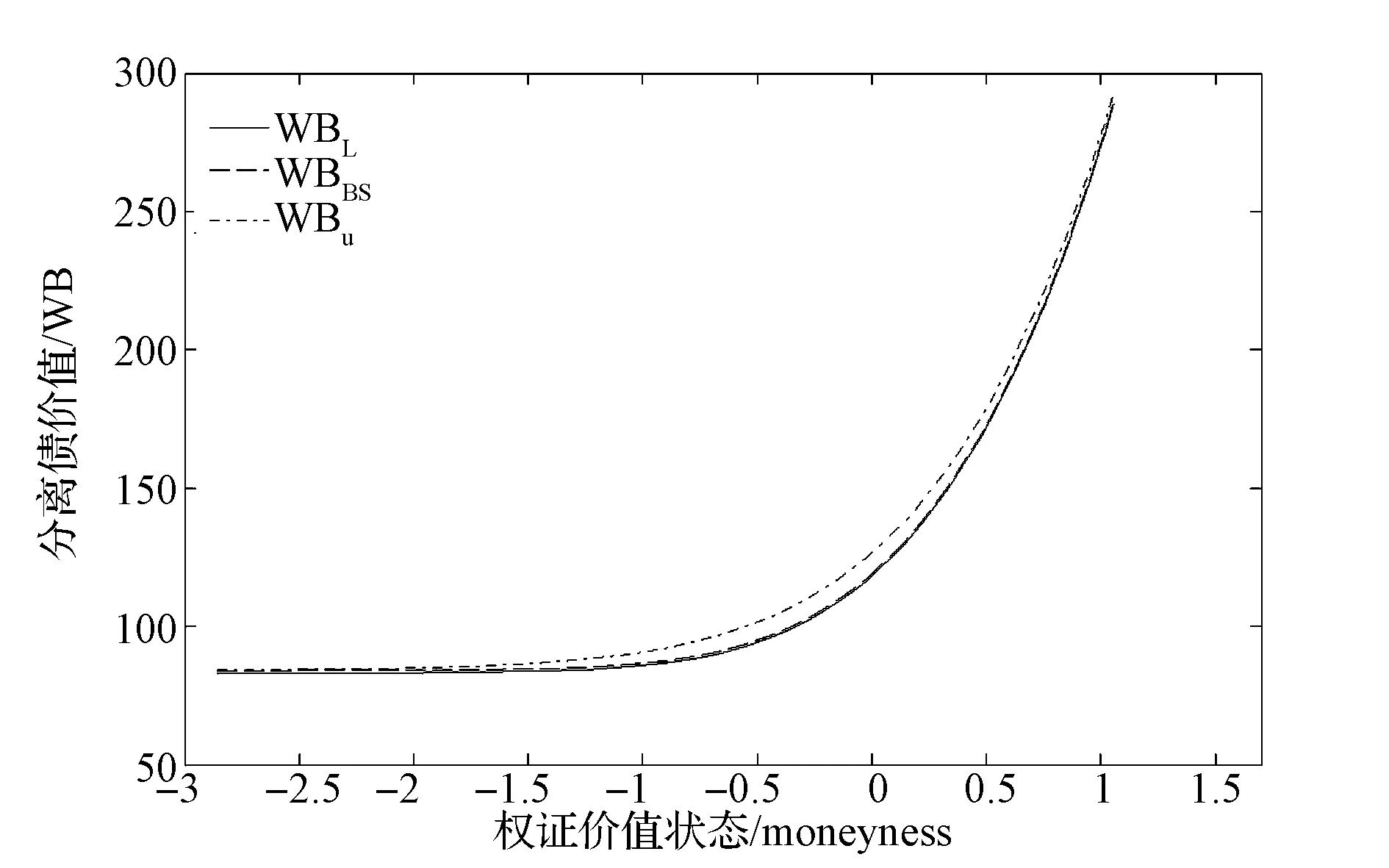
在研究投资组合约束对期权价值的影响时,Karatzas和Kou[21]将投资组合中标的股票可行集设定为[-l,u],l>0,u>0,它表示投资者买空和卖空的股票市值最多分别为个人财富总和的u和l倍。他们发现欧式看涨期权的价值与l无关,只与u有关,据此,本文将其中的股票可行集[-l,u],l>0,u>0定义为买空约束集。具体而言,当0 图1 买空约束下欧式看涨期权的价值 设当前时刻为0,根据BS经典假设的推论,公司股票收益率服从如下过程 dlnS=(μ-σ2/2)dt+σdw (1) 其中μ和σ为常数,w为现实测度下的标准维纳过程,S为公司股票价格。 在到期时刻T,如果分离债持有人行使转股权,则可以将债券按事先约定的转股比率η换算成公司股票。同时,这一转股行为还会对公司原有流通股本造成稀释,假设公司总流通股本数为N,直到分离债行权该总数变为N+n,则稀释因子ρ=N/(N+n)。将这两个因素纳入到Karatzas和Shreve[11]的模型中,便得到买空约束下分离债中的权证价值上界: (2) φ(ST)= (3) 其中,r为市场无风险利率,F为截至当前时刻的信息集,Eq为风险中性测度q下的数学期望,X为分离债的面额(相当于期权协议价格),ST为到期日行权前瞬间的股价。 联立式(1)~(3)并求解,便得到如下命题: 命题1u约束下分离债权证部分无套利价格上界为: (4) 其中 证明 对式(1)在[0,T]上求积分得: lnST=(μ-σ2/2)T+σ(wT-w) 取上式的指数形式,再根据Girsanov[22]中的定理,将现实测度转换到风险中性测度q可得: (5) 将式(5)代入式(3),然后将结果代回式(2),再对式(2)求积分得(其中h(·)为正态分布密度,参数d1的定义与前述一致): 证毕 接下来,我们来讨论投资组合约束下分离债中债券部分的价值。 2.2卖空约束对债券部分的影响 由上文对分离债的第一和第三条定性描述可知,将分离债的债券部分视为依赖于市场利率和公司资产状况的零息债是一种较合理的简化。 在衍生资产定价的经典理论[23]中,通常认为衍生资产与原生资产风险同源。又由于考察期内公司负债水平不变,结合式(1)可知,公司资产负债比的增长率将大致服从如下过程: (6) 其中,μv和σv分别表示公司资产负债比增长率的预期值和波动率,由Ronn和Verma[24]的推论可知: σv=σdlnv/dlnS (7) 与前文分析股票看涨期权的思路类似,可以得到如下命题: 命题2 在卖空约束下,一份标的价值为v、协议价格为1、到期日为T的欧式看跌期权,其无套利价格上界为: (8) 其中: 证明 与看涨期权类似,看跌期权价值及其到期盈亏分布如下: 将两式联立,并代入d2,有: 命题3 卖空约束下的分离债债券部分的价值下界为: (9) 证明 (10) 则投资人可以通过构造一个投资组合∏来实施无风险套利,即买入一份债券B和X份协议价格为1的欧式看跌期权p,并卖空一份面额为X的无风险债券,组合中的所有证券均在时刻T时到期。于是,该投资人在期初的现金流为: ∏=e-rTX-Xp-B (11) (12) 联立式(10)~(12),利用不等式的传递性可知: (13) 即该投资者在期初有正的现金流入。 在到期时刻T,上述组合的价值变为: ∏T=min(vTX,X)+Xmax(1-vT,0)-X=0 (14) 即该投资者在期末没有现金流入或流出。 可见,∏确实是一个可行的无风险套利组合。这种情形下,市场上的套利力量将会建立大量的∏多头以实施套利,直到市场恢复至∏的期初现金流也为0的状态时为止。这与无套利均衡原则相悖,故原假设不成立,从而期初的现金流∏也必然为0。 因此,直接将∏=0代入式(11)并联立式(12),便得到市场均衡的条件: (15) 即公司债券的价格下界: 证毕 2.3投资组合约束下的分离债模型 令无约束时基于BS公式得到的分离债价格为WBBS,由上文分析得知,WBBS必然也是有约束时分离债的一个价值边界,不妨将此时异于WBBS的另一个价格边界设为WBuL。由于分离债的价值完全由权证部分和债券部分构成,根据命题1~3,联立式(4)、(7)、(8)和(9)便得到其在投资组合约束下异于WBBS的无套利价格边界WBuL,即: (16) 其中 σv=σdlnv/dlnS 假定某上市公司期初的杠杆水平为40.00%,并且在考察期内其负债水平不变,当前股价为15.00元/股,经估计得到其股票和公司资产收益率的波动率分别为0.30和0.22,公司发行的零息分离债的面额为100.00元,转股价为16.67元/股,分离债和公司其他债务的剩余期限均为6.00年,全部分离债对股本潜在的稀释效应为0.96。交易所6.00年期国债到期年化收益率为2.90%。在市场的投资组合约束下,投资该公司股票的可行集上界及其资产的投资可行集下界绝对值均为2.00(即u=L=2.00)。据此,我们来确定该分离债的合理价格区间。 将上述数据依次代入分离债模型(16),计算结果为116.24元,而利用BS得到的无约束下的价格为109.64元。因此,该分离债的无套利价格区间就为[109.64,116.24](元)。 回顾第二节中的图1可知,不同的约束程度对应的无套利区间也不一样。为了比较两类约束(即买空约束和卖空约束)对分离债价格影响的差异,我们考察u∈(1.00,2.00],L∈(0,1.00]时,无套利区间的变化规律。结果见图2。 图2 不同约束下分离债价格区间的变化 与上文一致,图中的WBBS表示无约束时的分离债价格(下同),WBuL表示有约束时的分离债异于WBBS的价格边界。从图2可以看到,有约束的分离债价格边界WBuL会随着u的增加(即股票买空约束弱化)而减小,显然这与图1所呈现的结果也是一致的;相反,WBuL会随着L的增加(即公司资产卖空约束弱化)而增加,这主要是由于分离债的债券部分相当于包含了公司资产看跌期权空头。另外,还可以看到有约束的分离债价格是u的凸函数,而又是L的凹函数,这显然也是由分离债中的权证部分和债券部分对应的期权头寸差异所引起的。 由于分离债的行权价是事先约定的,因此,当股价变化时,分离债中的权证就处于不同的价值状态(Moneyness),从而对应的有约束价格也会发生相应的变化。现假定股价在[1.00,50.00](元)的区间内变动,我们分别来考察买空约束下和卖空约束下的价格变化规律。代入算例中的其他数据,运算的结果见图3。 图3 分离债价值随权证价值状态的变化(杠杆为40.00%) 图中,WBu表示只考虑买空约束时的分离债的价格下界,WBL表示只考虑卖空约束时的分离债的价格上界。通过观察发现,当权证处于深度实值状态(Deep in-the-money)时,两类约束对应的无套利价格区间都会显著缩小(即有约束价格上界/价格下界与无约束价格(WBBS)之间的差距在减小);当权证处于深度虚值状态(Deep out-the-money)时,只有买空约束的无套利价格区间在缩小,而卖空约束的无套利价格区间相对于其在值状态(At-the-money)时所发生的变化不显著。造成这种差异的主要原因是权证价值状态更依赖于标的股价而非公司价值,为了验证这一点,我们不妨考察一下其他杠杆水平下的情形。 图4 分离债价值随权证价值状态的变化(杠杆为20.00%) 将算例中的杠杆水平调整为20.00%,我们便得到如图4所示的结果。比较图3和图4不难发现,杠杆水平下降以后,卖空约束的无套利价格区间显著缩小,而买空约束的无套利价格区间几乎不变。这是由于,卖空约束主要是通过影响债券部分的价值进而改变分离债价格区间,而债券部分的价值又要受到杠杆水平的影响,因此,卖空约束下的无套利价格区间必然与杠杆因素息息相关。 依据分离债的自身特点,并结合市场客观存在的交易限制,本文建立了适用于投资组合约束下分离债定价的结构化模型。在此基础上,得到关于分离债的一个无套利价格区间,而在该区间内的套利策略都将是有风险的(投资组合约束的风险)。本文的研究结论主要有以下三点: 其一,由于分离债的权证部分相当于公司股票看涨期权多头,而债券部分相当于包含了公司资产看跌期权空头,使得有约束时分离债异于无约束价格的价格边界随股票买空约束程度的弱化而减小,二者表现为凸函数的变化关系。显然,这种函数凹凸性的背后所反映的其实是期权的头寸差异。 其二,当分离债权证处于深度实值状态(Deep in-the-money)时,投资组合约束下的无套利价格区间会显著缩小;当权证处于深度虚值状态(Deep out-the-money)时,只有买空约束的无套利价格区间在缩小,而卖空约束的无套利价格区间相对于其在值状态(At-the-money)时所发生的变化不显著。造成上述差异的主要原因是权证价值状态更依赖于标的股价而非公司价值。 其三,当公司杠杆水平发生变化时,卖空约束的无套利价格区间会发生显著的同向变化,而买空约束的无套利价格区间几乎不变。这是因为,卖空约束主要是通过影响债券部分的价值进而改变分离债价格区间的,而债券部分的价值又要受到杠杆水平的影响。 上述结论表明,利用有约束的模型不仅可以从现实价格中得出传统模型无法得到的投资组合约束的大小,还可以捕捉到公司杠杆的实时变化,从而使投资者获取投资组合约束及公司财务等方面信息的效率得以提高。不过,在刻画分离债中权证部分的价值时,由于本文将其视为到期行权的情形,因此,当存在引发投资人提前行权的潜在因素(如较高的分红,其他附属条款的约束等)时,本文模型将不再适用。 从引言的描述中可知,分离债的附属条款往往比转债要少,这也意味着后者的定价问题相对而言要更为复杂。本文对简单情形下的投资组合约束做了初步探索,也为未来涉及更为复杂的情形(如多附属条款、多关联资产等情形)的研究提供了参考。 [1] Tsiveriotis K,Fernandes C.Valuing convertible bonds with credit risk[J].Journal of Fixed Income,1998,8(2): 95-102. [2] Finnerty J D.Valuing convertible bonds and the option to exchange bonds for stock[R].Research Paper,Fordham University School of Business,2007. [3] Constantinides G M.Warrant exercise and bond conversion in competitive markets[J].Journal of Financial Economics,1984,13(3):371-397. [4] Philips G A.Convertible bond markets[M].London: Palgrave Macmillan,1997. [5] Ferris S P,Jo H,Pinkerton J M,et al.The usage of convertible and warrant bonds by Japanese firms: Risk-shifting or the delayed issuance of equity?[J].Advances in Financial Economics,2002,7(02):185-207. [6] 刘娥平,史扬.分离债与转债发行条款的比较分析[J].财会通讯(学术版),2007,(11): 100-103. [7] Black F,Scholes M.The pricing of options and corporate liabilities[J].Journal of Political Economy,1973,81(3):637-654. [8] Merton R.On the pricing of corporate debt:The risk structure of interest rates[J].Journal of Finance,1974,29(2):449-470. [9] Finnerty J D,Emery D R.Options in structured notes: Fix the price or fix the spread? [R].Research Paper,Fordham University Schools of Business,2014. [10] Huang Jingzhi,Huang Ming.How much of the Corporate-treasury yield spread is due to credit risk[J].The Review of Asset Pricing Studies,2012,2(2):153-202. [11] Karatzas I,Shreve S.Methods of mathematical finance[M].New York: Springer,2004. [12] 陈盛业,宋逢明.卖空约束下的公司债券定价[J].运筹与管理,2007,16(2):94-112. [13] Ingersoll J.An examination of corporate call policies on convertible securities[J].Journal of Finance,1977,32(2): 463-478. [14] Brennam M J,Schwartz E S.Convertible bonds:Valuation and optimal strategies for call and conversion[J].Journal of Finance,1997,17(5):1699-1715. [15] 杨大楷,杜新乐,刘庆生.浅论我国可转换债券的定价及设计[J].中国管理科学,2001,9(4):7-15. [16] Kraft H,Steffensen M.A dynamic programming approach to constrained portfolios[J].European Journal of Operational Research,2013,229(2): 453-461. [17] Fahim A,Huang Y J.Model-independent superhedging under portfolio constraints[J].Finance and Stochastics,2016,20(1): 51-81. [18] 徐枫,胡鞍钢,郭楠.异质信念、卖空限制对证券发行决策的影响[J].中国管理科学,2013,21(2):1-8. [19] 方立兵,曾勇.股市收益率高阶矩风险的产生机制检验[J].中国管理科学,2016,24(4):27-36. [20] Hong H,Stein J C.Differences of opinion,short-sales constraints,and market crashes[J].Review of Financial Studies,2003,16(2):487-525. [21] Karatzas I,Kou S G.On the pricing of contingent claims under constraints[J].The Annuals of Applied Probability,1996,(6): 321-369. [22] Girsanov I V.On transforming a certain class of stochastic processes by absolutely continuous substitution of measures[J].Theory of Probability &Its Applications,1960,5(3): 285-301. [23] Merton R C.Option pricing when the underlying stock returns are discontinuous[J].Journal of Financial Economics,1976,3(1): 125-144. [24] Ronn E I,Verma A K.Pricing risk-adjusted deposit insurance: An option-based model[J].The Journal of Finance,1986,41(4): 871-895. Abstract: Warrants bond is one of innovative financial instruments on investment and financing markets in recent years.The traditional approach to model warrants bond is to copy the pricing theory of convertible bond.In this paper,theory is combined with practice in real life to compare the terms and conditions of warrants bond and convertible bond and it is found that there are many differences between those two bonds,including coupon,maturity,exercise price,put and call provisions and credit etc.Therefore,it is necessary to build a more suitable pricing model for warrants bond. Learning from Tsiveriotis and Fernandes(1998),it is recognized that equity and debt components of warrants bonds are also subject to different default risk and derived a pair of coupled differential equations that can be solved explicitly.Basic value of warrants bond includes two parts,warrant’s value and bond’s value,where the latter is proved to be equivalent to a risk-free bond minus corresponding quantity put options.Dilution rate when conversing should be the dilution rate of equity ration.Besides,considering the domestic market still exists some investment restrictions currently,warrants bond is valued within the framework of structure models and a new pricing model is established under portfolio constraints in the markets.Based on those,contingent claims are modelled under this market hypothesis,and the assumptions of Black and Scholes(1973) pricing model is relaxed,introducing more realistic factors,studying warrants bond pricing problem under different market conditions in depth. The pricing of warrants bonds which in unconstrained case is presented.The pricing of warrants bonds and investment portfolios under prohibition of short-selling and borrowing are discussed. As portfolio constraints obviously exist in reality,it is meaningful to build such a structure model.It shows that the model not only can reflect portfolio constraints in the markets,but also can capture the real-time changes on financial lever of the company very well. Keywords: warrants bond;structure model;portfolio constraints;moneyness Pricing Warrants Bonds under Portfolio Constraints HUChang-sheng1,CHENGZhi-fu1,CHENJing2,XIONGDe-chao1,3 (1.Economics and Management School of Wuhan University,Wuhan 430072,China;2.Gansu branch,Bank of Communications,Lanzhou 730070,China;3.Capital Operation Department of Changjiang Securities,Wuhan 430015,China) F830.91 A 1003-207(2017)09-0011-08 10.16381/j.cnki.issn1003-207x.2017.09.002 2016-10-24; 2017-04-02 国家自然科学基金资助项目(71671134) 程志富(1986-),男(汉族),湖南株洲人,武汉大学经济与管理学院博士研究生,研究方向:行为金融与资产定价,E-mail:jefchan@whu.edu.cn.

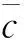

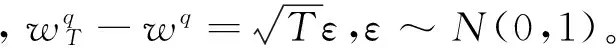
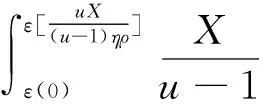
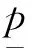
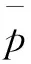

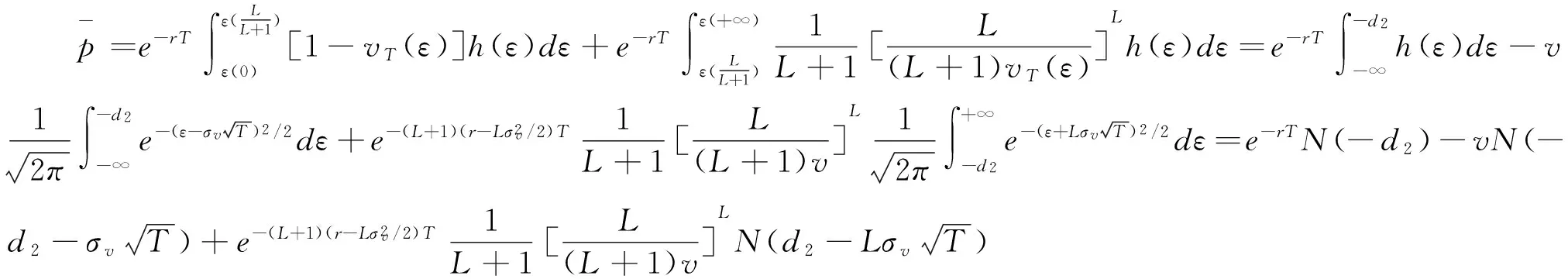
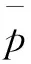



3 算例分析

4 结语
