BEM/FEM耦合螺旋桨静强度计算方法

叶礼裕，王超，李鹏，王锡栋

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

BEM/FEM耦合螺旋桨静强度计算方法

叶礼裕，王超，李鹏，王锡栋

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

［目的］螺旋桨强度的可靠性与船舶安全航行直接相关。为了快速且准确地计算螺旋桨强度，［方法］将边界元（BEM）和有限元法（FEM）耦合开发螺旋桨强度预报程序。运用低阶边界元法程序对螺旋桨进行水动力性能计算，并使用普朗特—许力汀平板摩擦阻力公式进行粘性修正，然后将计算得到的桨叶表面压力和粘性修正力作为有限元法结构计算的面力输入。针对螺旋桨结构形状的特殊性，发展实体螺旋桨有限元结构单元的自动划分方法，运用有限元结构计算方程计算出螺旋桨在表面压力和体积力作用下的应力与位移分布。以DTRC 4119模型桨为例，对提出的方法进行收敛性和网格无关性分析，并与文献的有限元软件计算结果进行比较，以验证其有效性。［结果］计算结果表明，提出的方法能够准确计算螺旋桨的应力和位移分布。［结论］该方法避免了人工建模及有限元网格划分的过程，具有实施程序简便、计算效率高等优点，可嵌入到螺旋桨的理论设计和优化设计过程中，形成快速计算螺旋桨强度的能力，提高螺旋桨设计的效率。

螺旋桨；强度预报；边界元法；有限元法；应力分布

Abstract：［Objectives］The reliability of propeller stress has a great influence on the safe navigation of a ship.To predict propeller stress quickly and accurately,［Methods］a new numerical prediction model is developed by coupling the Boundary Element Method（BEM）with the Finite Element Method(FEM).The low order BEM is used to calculate the hydrodynamic load on the blades,and the Prandtl-Schlichting plate friction resistance formula is used to calculate the viscous load.Next,the calculated hydrodynamic load and viscous correction load are transmitted to the calculation of the Finite Element as surface loads.Considering the particularity of propeller geometry,a continuous contact detection algorithm is developed; an automatic method for generating the finite element mesh is developed for the propeller blade;a code based on the FEM is compiled for predicting blade stress and deformation;the DTRC 4119 propeller model is applied to validate the reliability of the method;and mesh independence is confirmed by comparing the calculated results with different sizes and types of mesh.［Results］The results show that the calculated blade stress and displacement distribution are reliable.This method avoids the process of artificial modeling and finite element mesh generation,and has the advantages of simple program implementation and high calculation efficiency.［Conclusions］The code can be embedded into the code of theoretical and optimized propeller designs,thereby helping to ensure the strength of designed propellers and improve the efficiency of propeller design.

Key words：propeller；strength prediction；Boundary Element Method（BEM）；Finite Element Method（FEM）；stress distribution

0 引 言

螺旋桨作为船舶航行过程中的动力来源，一直以来是船舶设计的重要关注点。螺旋桨结构的可靠性是保证船舶航行性能满足要求的前提条件，故对航行安全有着重要意义。然而，随着船舶朝大型化、高速化方向发展，大功率主机的应用导致螺旋桨桨叶的表面负荷增大，而大侧斜螺旋桨的广泛应用使螺旋桨的强度问题变得更加突出。当螺旋桨工作时，其产生的推力和旋转阻力对桨叶具有弯曲和扭转的作用，而且螺旋桨旋转产生的离心力还会造成桨叶弯曲以及沿展向外拉伸。若螺旋桨强度不足，可能会使螺旋桨发生破损或断裂，或因变形大而导致螺旋桨的水动力性能无法满足设计要求。因此，为了提高螺旋桨设计效率和保证螺旋桨桨叶的强度，迫切需要开发一种能准确、快速预报螺旋桨桨叶强度的方法。

目前，螺旋桨桨叶强度预报可采用规范校核、数值预报和模型试验等方法。国内外有关规范都规定了强度校核的方法和要求，但均是基于大量的使用经验而提出，其预报结果比较保守。在模型试验方面，Boswell［1］对大侧斜螺旋桨桨叶（片）进行了静态应力测量试验；赵波［2］开展了大侧斜螺旋桨的静态应力试验和动态应力试验，并与理论计算结果进行了对比；杨向晖等［3］通过在大侧斜桨模表面粘贴应变片的方法研究了不同工况下桨叶的应变和应力分布。从以上研究和试验的结果来看，螺旋桨强度模型试验成本较高，试验难度大且耗时多，无法广泛应用。

螺旋桨强度数值分析方法主要采用悬臂梁法和有限元法。悬臂梁法是一种比较方便且可行的桨叶应力预报方法，但该方法将桨叶简化为变截面扭曲的悬臂梁，这一缺陷使得不能精准预报螺旋桨的强度［4］。对于有限元法，开展较多的是采用CFD计算与有限元分析软件结合的方法来预报桨叶应力分布［5-6］，也有学者将边界元法和有限元分析软件对接预报桨叶应力分布［7-8］。这种方法虽然能准确预报螺旋桨桨叶的应力分布，但需要复杂的建模、网格划分过程，不利于螺旋桨的设计，而且将边界元程序与有限元软件对接存在接口稳定性不足的问题。还有学者自编有限元程序开展螺旋桨的强度计算，如胡寿根等［9］将螺旋桨桨叶视为厚壳单元，将桨叶拆分为12个单元，编制了相应的应力分析程序；王玉华［10］专门针对大侧斜桨开发了有限元强度计算程序HPROP，将升力面法计算得到的压力值输入到有限元程序中进行计算；刘竹青等［11］将边界元和有限元计算程序HPROP相结合进行了螺旋桨水动力载荷作用下的强度计算。对于采用自编的有限元程序进行的强度计算，上述文献并未详细介绍具体的实施过程。从计算图可知，它们对实体螺旋桨的有限元结构单元划分存在一定的局限性，其结构单元数量较少，可能会带来计算精度不足的问题。

本文将研究BEM/FEM耦合螺旋桨强度计算方法，提出一种准确和快速预报螺旋桨强度的方法，为设计阶段的螺旋桨强度评估提供一种较好的思路。总体上，该方法是将边界元法计算得到的螺旋桨表面压力传递到螺旋桨有限元结构计算中，这里需要解决的问题是如何在螺旋桨表面网格划分固定的情况下建立一种有限元结构单元的自动划分方法，以实现水动力载荷在两种方法之间的传递。为此，本文将详细介绍有限元法计算螺旋桨强度的有关理论及具体的数值计算过程，采用Fortran语言编译有限元法预报螺旋桨强度的程序，并将其与螺旋桨定常边界元法的性能预报程序对接。最后，以某螺旋桨桨叶强度预报为例，验证本文所提方法的有效性。

1 边界元法理论

螺旋桨边界元法不对物体形状作出任何假设，其在真实物面上满足边界条件，能比较精确地预报螺旋桨的水动力性能，故近年来得到了广泛应用。

图1所示为固定于桨叶的直角坐标系O-XYZ和柱坐标系O-XRθ。图中，R，θ分别为径向坐标向量和角度坐标向量。假设螺旋桨在来流速度V0的情况下以角速度ω转动，利用格林公式将用于描述不可压、无粘、无旋的势流问题的拉普拉斯方程转化为物体边界上的积分方程，使求解物体绕流问题转化为求解任意物面上未知节点的强度问题［12］。

图1 螺旋桨的坐标系Fig.1 Ccoordinates of propeller

在螺旋浆表面SB上,有

式中：SW为尾涡面；ϕ为扰动速度势；RPQ，RPQ1分别为场点P到螺旋桨表面点Q以及到尾涡面点Q1的距离；nQ，nQ1分别为螺旋桨表面上点Q和尾涡面点Q1的单位法向量；Δϕ为通过尾涡面SW的速度势跳跃，在SW上可表示为

式中：上标“+”和“-”分别表示在尾涡面上、下表面的值。

对于螺旋桨的定常问题，尾涡面速度势跳跃Δϕ在同一半径处为常量。由法向偶极子分布与涡环分布的等价关系可知，Δϕ即为尾涡强度，可在升力体的尾缘处满足库塔条件来确定该尾涡强度。库塔条件有多种形式，这里采用压力库塔条件，它要求在升力体的尾缘处上、下表面的压力差(Δp)TE为0，即

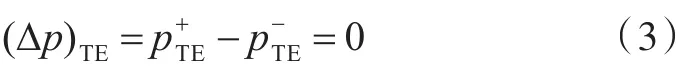
式中，下标TE表示螺旋桨随边。

结合库塔条件，可以迭代求解得到线性方程组的数值解，即物体表面的扰动速度势ϕ。可以利用柳泽发展的方法由物体表面上的速度势确定物体表面上的速度，然后通过伯努利方程计算螺旋桨表面上的压力。

2 有限元法计算螺旋桨的强度

2.1 螺旋桨有限元网格自动划分方法

有限元法是将复杂的连续介质求解区域离散为一组有限多个且按一定方式相互连接在一起的单元组合体。由此可知，网格划分是有限元分析的关键技术之一，也是有限元数据准备过程中耗时最多、工作量最大的工作，所以在有限元技术发展过程中一直倍受关注。本节着重介绍螺旋桨有限元网格的自动划分方法。通过程序编译后，使用者只需输入螺旋桨的型值表，即可实现螺旋桨有限元结构的体单元在计算机上自动完成。该方法使用简单、性能可靠，生成的单元质量较好。

图2 桨叶剖面的表达Fig.2 Expression of blade section

由于螺旋桨的几何形状比较复杂，为生成结构单元的节点坐标，首先需要对桨叶表面的坐标进行几何表达。在图2所示的柱坐标系中，s1为桨叶剖面上点到导边的弦向距离，c1为桨叶剖面上导边至母线的距离，xr为桨叶剖面处的纵倾，θs为剖面侧斜角，β为螺旋桨几何螺距角，yb和yf分别为桨叶叶背、叶面上的点到弦线的距离，下标b，f分别表示螺旋桨的叶背和叶面。则在柱坐标系O-XRθ下，螺旋桨半径R处叶剖面上点的坐标可表示为

在坐标系O-XYZ下的相应坐标为

在边界元法计算中，将螺旋桨表面划分为一系列的小单元，并用双曲面元代替每个单元，如图3所示。这里在弦向和展向分别采用余弦分割，展向节点rj表示为

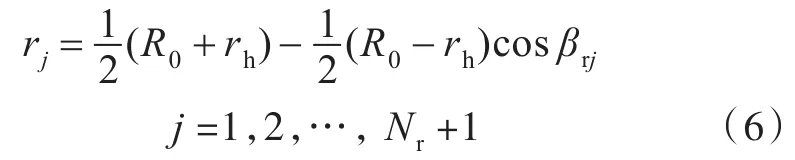
弦向节点si表示为

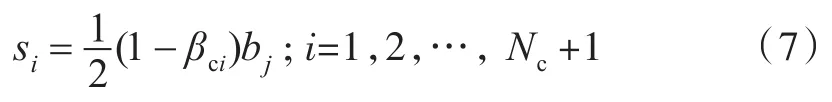
式中：R0，rh分别为螺旋桨半径和桨毂半径；bj为rj处的叶剖面弦长；Nr，Nc分别为展向和弦向的网格数；βrj，βci分别为展向节点角度和弦向节点角度，并表示如下：

考虑到螺旋桨结构的特殊性，本文对螺旋桨的实体结构沿展向、弦向以及厚度方向进行网格划分，形成8节点的六面体单元，如图3所示。为了更好地对接边界元法预报程序，以便将水动力载荷传递到有限元结构计算中，桨叶展向和弦向的划分方式与边界元法相同，故螺旋桨有限元实体结构外层的节点坐标与边界元法面网格节点坐标是重合的。这里弦向和展向采用余弦分割，主要目的是对导边/随边、叶根/叶梢进行加密以反映这些区域的几何特点。桨叶厚度方向采用平均分割。

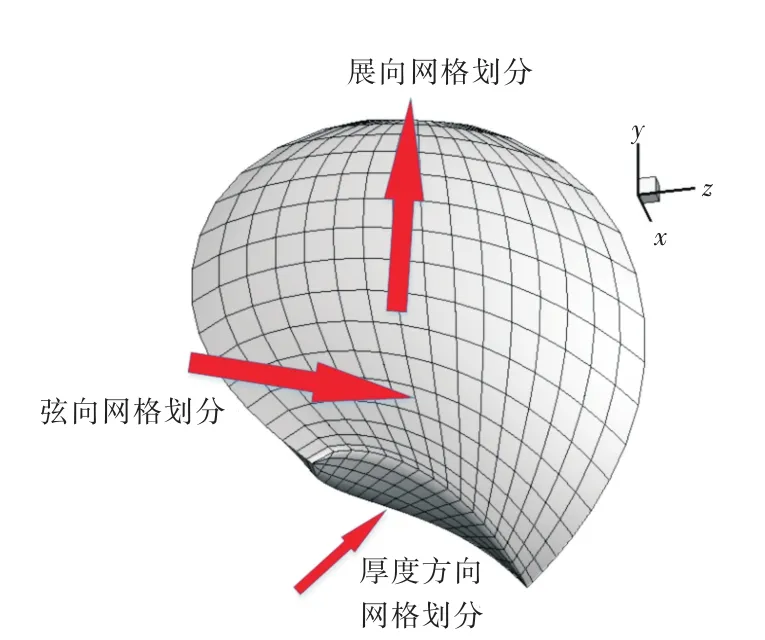
图3 桨叶有限元模型Fig.3 FE mesh model of propeller blade

与四面体相比，六面体单元具有更好的收敛性，达到同样精度所需的六面体单元和节点数要远小于四面体单元［13］。六面体单元划分的实体不仅分析结果比四面体单元的好，而且离散后的单元数也远小于四面体单元的单元数［14］。此外，六面体单元具有从几何形态上更加容易辨认的优点。因此，分析人员很愿意采用六面体单元来完成三维实体的有限元分析。通过对螺旋桨实体结构的展向、弦向以及厚度方向的网格划分，除导边和随边外，其他部位被划分为8节点的六面体，而导边和随边处则被划分为五面体单元。本文将五面体单元中导边上的线条看成是空间四边形退化成一条直线段的情况，在有限元计算中依然可以将其看作是8节点的六面体，如图4所示。

图4 六面体结构单元的生成Fig.4 Generation of the hexahedral element

2.2 总体刚度矩阵和力的平衡方程

由上节可知，本文考虑到螺旋桨结构的特殊性，采用8节点的六面体单元来划分螺旋桨的实体结构。这里以8节点的六面体单元为例来介绍有限元法相关理论。

对于在旋转坐标系中水动力载荷作用下的螺旋桨，其总体有限元结构动力学方程可以表示为

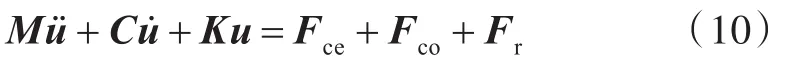
式中：M，C和K分别为总体附加惯性力矩阵、附加阻尼力矩阵、刚度矩阵；ü，u̇，u分别为节点的加速度、速度和位移；Fce，Fco和Fr分别为离心力、科氏力和水动力载荷。

对于在均匀流中的螺旋桨，当以固定转速旋转时，其受到的水动力载荷为定常载荷，节点的加速度ü、速度u̇以及科氏力Fco为0，则式（10）可以简化为

由于有限元法是将实体结构划分为单元，故将所有单元的刚度集成和叠加可得到总体刚度矩阵K，总体节点力列阵F=Fce+Fr则由所有单元的等效节点力集成和叠加而成。式（11）可离散为一个大型线性方程组，结合已知的位移边界条件和力边界条件，可求解得到位置的节点位移和节点力。

式中：σx，σy，σz分别为x，y，z方向上的正应力；τxy为法向面x方向且平行于y轴的剪切应力；τyz为法向面y方向且平行于z轴的剪切应力；τzx为法向面z方向且平行于x轴的剪切应力。

2.3 单元基本方程和刚度矩阵

应用虚位移原理和虚功方程，可以推导得到空间问题中单元的基本方程为［15］

式中：Ke为空间单元的刚度矩阵，上标e代表单元；ue为单元节点的位移列阵；Fe为单元等效节点力列阵。计算方法将在第2.4节介绍。

空间单元刚度矩阵Ke可表示为

式中：De为单元弹性矩阵；Be为单元应变矩阵，写出分块矩阵的形式为

其中，

式中，Ni为插值函数；分别为

式中，a为单元边长；ξ，η，ζ为等参元局部坐标系。

单元弹性矩阵De为由弹性模量E与泊松比μ决定的常数矩阵，由式（18）计算得到。

式（18）是在单元结构比较规则的条件下推导得出。对于8节点的六面体单元，式（18）只适合于计算正六面体单元。由于螺旋桨结构复杂，实际上对螺旋桨实体结构划分后得到的六面体是不规则的，需要引入等参元进行坐标转换。通过等参元坐标转换后，得到如下在局部坐标系中的单元刚度矩阵通式。

2.4 非节点载荷移置

结构离散后，各单元通过节点连接，结构位移近似地由所有节点的位移表示，所有外载荷都要等效地移置到单元节点上，以用于单元特性分析。根据弹性力学的虚位移原理，可将外载荷移置到单元节点上。

式中，N为形函数矩阵。螺旋桨不受到集中力作用，这个力的大小设置为0。

螺旋桨因旋转效应将引起离心力，可以将其处理成体积力，其计算表达式为

式中：ρ为螺旋桨材料密度；ω为螺旋桨的旋转角速度；X为节点坐标向量。如果单元e的某一界面上分布有面力，将微分面dA上的力（A为单元面积）作为集中力，可得到移置后的等效节点力列阵为

对于螺旋桨而言，主要是螺旋桨旋转过程中桨叶受到水动力载荷和粘性阻力的作用。基于本文建立的螺旋桨有限元网格自动划分方法，可使螺旋桨有限元实体结构外层面元与边界元法面元重合。因此，边界元法计算得到的螺旋桨面元中心处的压力分布，可作为面力施加到有限元结构中，并通过式（26）等效地移置到单元节点上。

从而得到单元基本方程Keue=Fe中的单元等效节点力列阵Fe。

3 计算流程

本文采用双向流—固耦合方法，即边界元法预报的计算结果和有限元法预报的结构计算结果是相互传递的，两种方法在迭代时由于边界条件的改变而开始了新的计算。信息在流体和结构模块中往复传递，直至获得满足收敛条件的解为止。图5所示为本文计算流程图，具体的迭代求解过程如下：

1）基于速度势的低阶边界元法，对每个桨叶布置的双曲面元求解式（1）获得扰动速度势ϕ，利用伯努利方程求解得到面元控制点的压力分布和水动力性能。

2）将螺旋桨表面压力分布和结构单元旋转引起的离心力施加到有限元体单元中，通过整个结构的总体力平衡方程式（11），求解螺旋桨的应力和位移分布。

3）将有限元法计算得到的螺旋桨表面节点位移与边界元法点坐标相加，求解式（1）获得扰动速度势ϕ，利用伯努利方程求取面元控制点的压力分布和水动力性能。

4）重复步骤2）和步骤3），直到满足最大位移收敛条件为止。

图5 螺旋桨的流—固耦合求解过程Fig.5 Calculation process of fluid-solid interaction for propeller

4 计算模型和参数设置

本文以DTRC 4119模型桨为研究对象，考察网格数以及网格划分对计算结果的影响，并评估本文所提方法的可行性。其中，螺旋桨直径为0.305 m，毂径比为0.2，无纵倾，无侧斜，剖面翼型为NACA-66mod。螺旋桨材料选择为密度为7 600 kg/m3的镍—铝青铜，材料的弹性模量E= 113 GPa，泊松比μ=0.34。鉴于螺旋桨桨叶通常与桨毂采取刚性连接，为便于计算，本文模型将桨叶叶根处节点进行了六自由度刚性约束。计算工况设定为：设计进速系数为0.833，转速为600 r/min。

5 网格数和收敛性分析

根据以往在有限元方面的实践和研究发现，实体结构网格尺度的大小将直接影响计算结果的精度。本节借鉴相关性研究方法，预报螺旋桨在不同网格数情况下对计算结果的影响，并充分挖掘计算数据，以掌握计算结果与变量之间的相互关系，用于指导选取合适的螺旋桨网格数，使计算结果更准确，同时也不影响计算速度。

5.1 展向和弦向网格数

基于上述方法，采用10种网格划分方式，即弦向和展向网格数为10×10，12×12，14×14，16× 16，18×18，20×20，22×22，24×24，26×26和28×28，并将厚度方向的网格数固定为6，然后对计算结果进行分析。

图6和图7所示分别为将桨叶应力预报结果导入到Tecplot软件后得到的桨叶应力与位移分布，即在计算工况下，弦向和展向网格数分别为12×12，16×16和20×20时桨叶叶面的应力和位移分布。预报时，为便于比较，设置了相同的等高线取值范围。由图6可知，随着网格数的增加，桨叶应力不断增大，桨叶应力分布更加均匀；网格数过少时，容易导致桨叶应力峰值集中于某一点上。由图7可知，不同网格数得到的桨叶位移分布趋势基本一致，但是位移量的区别较大。

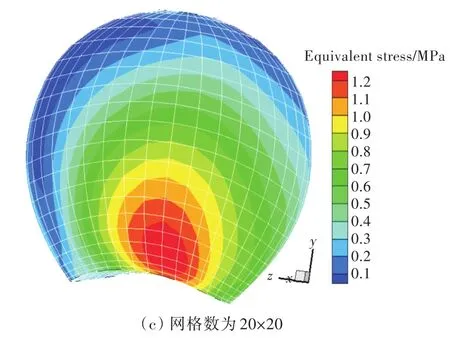
图6 弦向和展向不同网格数时计算得到的桨叶应力分布Fig.6 Equivalent stress distributions of blade with different chord-wise and span-wise mesh numbers

图7 弦向和展向不同网格数时计算得到的桨叶位移分布Fig.7 Displacement distributions of blade with different chord-wise and span-wise mesh numbers

为了更好地分析弦向和展向网格数对计算结果收敛性的影响，图8给出了在计算工况下弦向和展向不同网格数对应的最大等效应力与最大位移量。由图8可知，随着网格数的增加，最大等效应力和最大位移量均不断增大，但增大的幅度有所减小；当网格数达到24时，虽然最大等效应力和最大位移量还有增长的趋势，但增长的幅度已经很小。因此，弦向和展向网格数为24×24时基本可以认为计算结果收敛了。

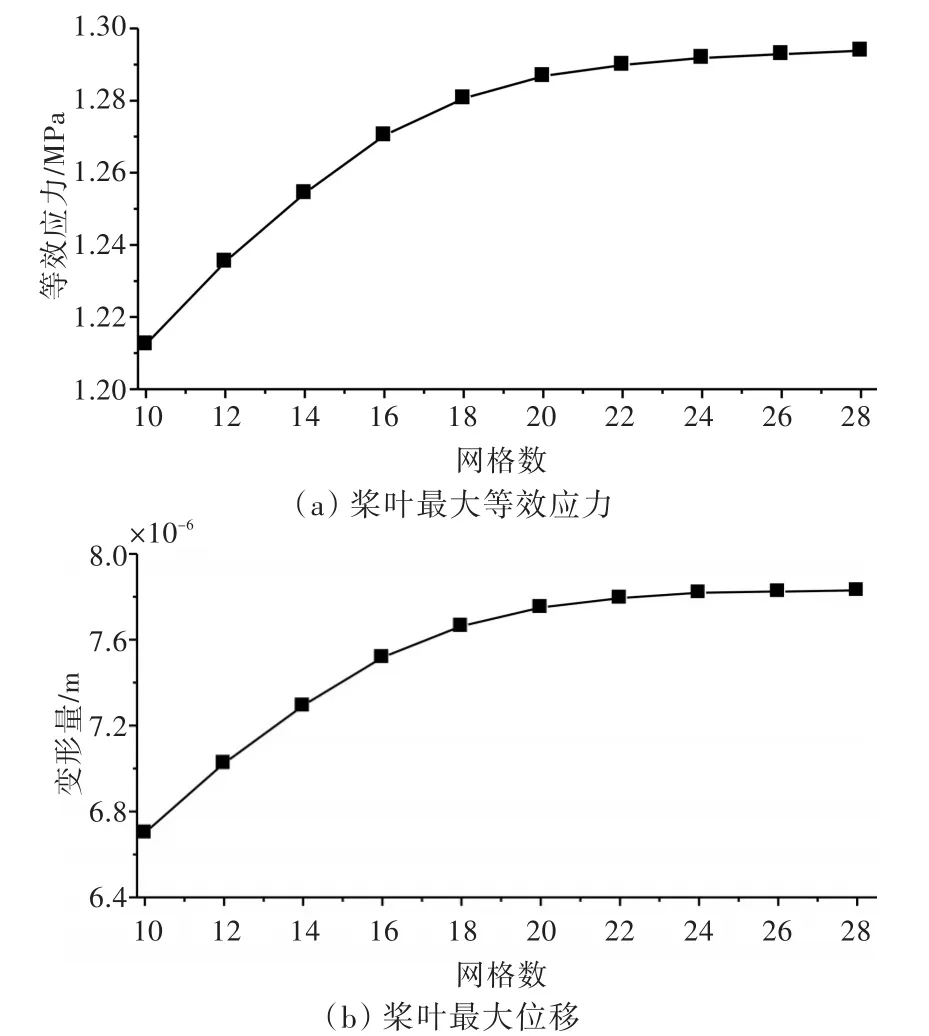
图8 网格收敛性分析Fig.8 Convergence process with different chord-wise and span-wise mesh numbers

5.2 厚度方向网格数目

基于上述方法，对厚度方向网格数为2，3，4，5，6，7，8的计算结果进行分析，将弦向和展向的网格数固定为24×24。厚度方向的网格数只对有限元网格单元的划分有影响，不会影响边界元法的网格划分，故在未开始流—固耦合迭代前，不同厚度方向的网格数水动力性能的计算结果相同。

图9和图10所示为在计算工况下厚度方向网格数为2，4和6的桨叶叶面应力与位移分布。为便于比较，设置了相同的等高线取值范围。由图9可知，厚度方向网格数对桨叶应力计算结果影响很大，随着网格数增加，红色区域范围越来越大，说明桨叶应力呈整体增大的趋势。由图10可知，不同网格数计算得到的桨叶位移分布趋势基本一致，但随着网格数的增加，红色区域范围变大，说明桨叶的位移也呈整体增大趋势。由此可见，厚度方向网格数对螺旋桨强度的计算结果影响很大。

图9 厚度方向不同网格数计算的桨叶应力分布Fig.9 Equivalent stress distributions of blade with different mesh numbers in thickness direction

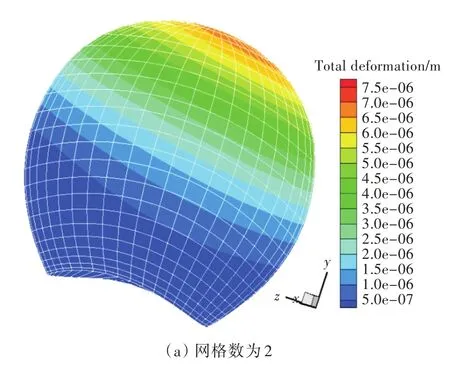
图10 厚度方向不同网格数计算的桨叶位移分布Fig.10 Displacement distributions of blade with different mesh numbers in thickness direction

为了更好地分析弦向和展向网格数对计算结果收敛性的影响，图11给出了在计算工况下不同厚度方向网格数计算得到的最大等效应力和位移量。由图11可知，随着网格数的增加，最大等效应力和位移量均不断增大，但增大的幅度迅速减小。因此当网格数增大到6以上时，基本可以认为计算结果收敛了。

6 方法验证

对于采用边界元法计算螺旋桨定常水动力性能的准确性方面，已有多篇文献［16-18］进行过验证，本文不再赘述，而重点关注本文提出的FEM/BEM耦合方法计算螺旋桨强度的准确性，即对螺旋桨强度计算的结果进行重点分析和验证。

图11 厚度方向网格收敛性分析Fig.11 Convergence process with different mesh numbers in thickness direction

为了验证本文方法预报螺旋桨强度的准确性，将本文应力预报结果与文献［19］进行了比较。根据上述网格数和收敛性分析，在计算螺旋桨的定常边界元法水动力性能时，螺旋桨表面的弦向和展向均采用半余弦分割，弦向和展向网格数为26×26。在计算工况下，本文采用边界元法计算程序得到的推力系数和扭矩系数分别为0.143 2和0.026 5，文献［19］计算得到的分别为0.135 2和0.028 1，模型试验测量得到的分别为0.141 2和0.027 8［20］。由此可见，与模型试验测量得到的推力系数和转矩系数相比，本文方法计算的结果与试验测量结果较为接近；与文献［19］的计算结果相比，本文计算得到的推力系数比文献［19］的大，扭矩系数比文献［19］的小。

本文对螺旋桨进行有限元静强度分析时，螺旋桨实体结构的弦向和展向与边界元法相同，厚度方向采用平均分割，网格数为8。

图12所示为本文方法预报得到的DTRC 4119模型桨叶背和叶面的应力分布。通过与文献［19］计算得到的分布结果比较，发现本文方法计算的桨叶应力分布趋势与文献［19］的结果基本一致。螺旋桨强度校核主要关注最大等效应力是否超过许用应力。本文计算的桨叶最大等效应力为1.31MPa，而文献［19］预报的最大等效应力为1.18 MPa，可见本文方法预报的结果相较于文献［19］的偏大。虽然两种方法计算得到的最大等效应力有一定的偏差，但从量级来看还是比较合理的。导致计算结果出现偏差的原因很多，其中包括：边界元法和CFD这2种方法预报的螺旋桨水动力载荷压力分布不可能相同；两种方法的有限元网格划分类型与数量不同；两种方法载荷施加和传递的方式不尽相同。另外应注意的是，本文方法计算得到的桨叶应力集中在弦向桨叶叶根的中部，与文献［19］得到的结论一致。

图12 桨叶应力分布Fig.12 Equivalent stress distributions of blade

图13所示为采用本文方法预报得到的DTRC 4119模型桨叶背和叶面的位移分布。由图13可知，叶面和叶背的位移量相同。本文方法计算得到的应力分布趋势与文献［19］计算的结果一致。桨叶位移主要影响螺旋桨的水动力性能，由于本文螺旋桨模型为刚性桨，位移量小，故不会引起水动力变化。本文计算得到的桨叶最大位移量为7.92×10-6mm，而文献［19］预报的最大位移量为7.0×10-6mm，可见本文预报得到的值有些偏大。

考虑到目前国内对螺旋桨的强度校核大多采用悬臂梁法，这里将本文方法与悬臂梁法的校核结果进行了对比，以验证本文方法的可信性。文献［4］提出了悬臂梁法和边界元法耦合的桨叶应力分布预报方法，由于悬臂梁的局限性，无法预报桨叶的位移。图14所示为文献［4］采取与本文相同工况时预报的DTRC 4119模型桨桨叶的应力分布。由图12和图14的对比可知，本文方法计算的桨叶应力分布趋势与悬臂梁法计算的结果类似，桨叶最大应力均集中在叶根的中部，但桨叶应力最大值却存在一定的差异。其中，悬臂梁方法预报的桨叶最大拉应力为1.03 MPa，相较于本文方法计算的结果，悬臂梁法预报的结果偏小。造成上述偏差的原因为：悬臂梁法将桨叶过度简化；两种方法采用的强度理论有所区别，悬臂梁法采用的是最大拉应力理论（第1强度理论），而本文方法采用的是形状改变比能理论（第4强度理论）。

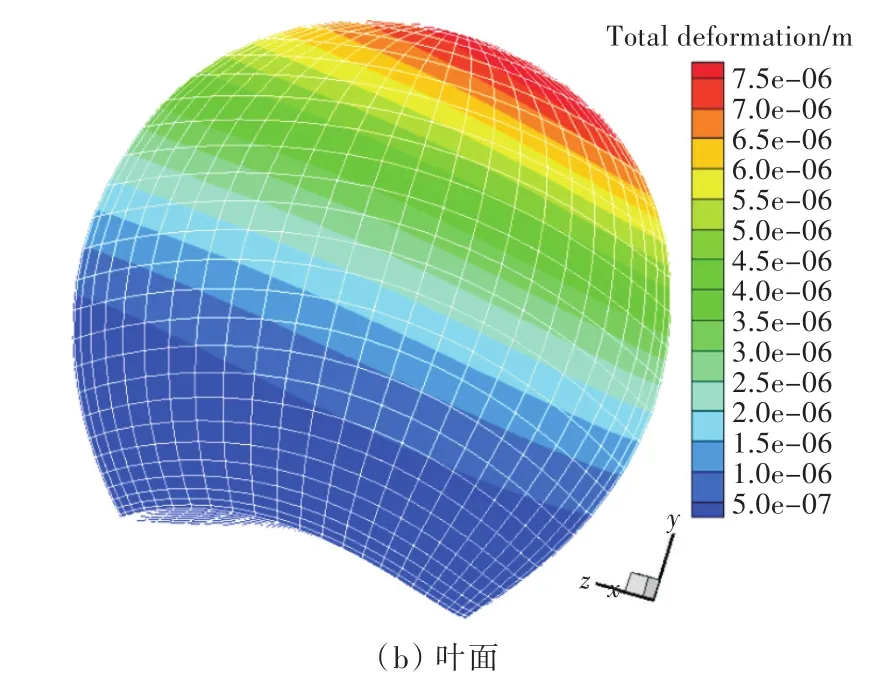
图13 桨叶位移分布Fig.13 Displacement distributions of blade

图14 悬臂梁法预报的DTRC 4119模型桨桨叶应力分布Fig.14 Stress distributions of DTRC 4119 blade predicted by the cantilever beam method

为了验证本文方法对大侧斜螺旋桨的适用性，预报了侧斜角度为36°的桨叶应力分布和位移分布，结果如图15所示。由图可知，桨叶最大应力发生在叶根且靠近随边的部位，与文献［8］得到的结论一致。

图15 本文方法预报的DTRC 4382模型桨桨叶应力和位移分布Fig.15 Stress and displacement distributions of DTRC 4382 predicted by current method

7 结 论

本文介绍了有限元法求解螺旋桨静强度的相关理论，分别提出和研究了一种螺旋桨有限元结构单元划分及BEM/FEM耦合预报螺旋桨静强度的方法，探讨了在桨叶弦向、展向及厚度方向采用不同网格数对计算结果和收敛性的影响，并将本文方法与相关文献计算的结果进行了比较，验证了本文方法的可行性。针对本文计算对象，分析得到如下结论：

1）对桨叶弦向和展向采用不同网格数对计算结果的影响分析表明：随着网格数的增加，桨叶应力分布更均匀，最大等效应力和最大位移量均呈不断增大的趋势，但增大的幅度迅速减小，桨叶弦向和展向的网格数需在26×26以上才可收敛。

2）对桨叶厚度方向采用不同网格数对计算结果的影响分析表明：随着网格数的增加，桨叶应力和位移呈整体增大的趋势，但增大的幅度迅速减小，在厚度方向的网格数需在6以上才可收敛。

3）采用本文方法计算得到的桨叶应力和位移分布与相关文献的计算结果吻合较好，说明本文方法简便、快速，可确保计算精度。

应用本文方法便于对螺旋桨的静强度进行分析，可快速计算螺旋桨桨叶的应力和位移分布，后续将在其他类型的螺旋桨中予以应用，以进一步对所提方法进行验证，并将该程序嵌入到螺旋桨理论设计和优化设计过程中，提高螺旋桨在设计阶段的强度评估和计算效率。

［1］BOSWELL R J.Static stress measurements on a highly-skewed propeller blade［R］.Washington，DC：Naval Ship Research and Development Center，1969.

［2］赵波.大侧斜螺旋桨强度研究［D］.武汉：华中科技大学，2003.

［3］杨向晖，程尔升.大侧斜螺旋桨桨叶应力测试研究［J］.船海工程，2004（1）：6-9.YANG X H，CHENG E S.Study on stress measurement of the high skewed propeller blades［J］.Ship& Ocean Engineering，2004（1）：6-9（in Chinese）.

［4］叶礼裕，王超，孙帅，等.基于悬臂梁法和面元法耦合的桨叶应力分布预报［J］.武汉理工大学学报（交通科学与工程版），2015（5）：968-973.YE L Y，WANG C，SUN S，et al.Prediction of blade stress distribution based on cantilever beam method and panel method［J］.Journal of Wuhan University of Technology（Transportation Science&Engineering），2015（5）：968-973（in Chinese）.

［5］黄毅，许辉，姜治芳.大侧斜螺旋桨强度校核探讨［J］.中国舰船研究，2010，5（5）：44-48.HUANG Y，XU H，JIANG Z F.Strength analysis of highly-skewed propeller［J］.Chinese Journal of Ship Research，2010，5（5）：44-48（in Chinese）.

［6］柳章存.船用螺旋桨的数值模拟及流固分析［D］.镇江：江苏科技大学，2012：1-8.

［7］陈悦，朱锡，黄政，等.水动力载荷下复合材料螺旋桨强度评估［J］.中国舰船研究，2015，10（1）：19-26.CHEN Y，ZHU X，HUANG Z，et al.Strength evaluation of the composite propeller under hydrodynamic fluid load［J］.Chinese Journal of Ship Research，2015，10（1）：19-26（in Chinese）.

［8］孙海涛，熊鹰.考虑变形的螺旋桨水动力及变形特性研究［J］.哈尔滨工程大学学报，2013，34（9）：1108-1112，1118.SUN H T，XIONG Y.Study on hydrodynamic and deformation performance of propellers considering the blade deformation［J］.Journal of Harbin Engineering University，2013，34（9）：1108-1112，1118（in Chinese）.

［9］胡寿根，王国强，汪庠宝.螺旋桨强度的厚壳元分析［J］.上海交通大学学报，1988，22（2）：33-42.HU S G，WANG G Q，WANG X B.Thick shell element method of stress analysis of propeller blades［J］.Journal of Shanghai Jiaotong University，1988，22（2）：33-42（in Chinese）.

［10］王玉华.大侧斜螺旋桨强度研究［J］.船舶力学，1998，2（2）：44-51.WANG Y H.Comparative studies on highly-skewed propeller strength［J］.Journal of Ship Mechanics，1998，2（2）：44-51（in Chinese）.

［11］刘竹青，陈奕宏，姚志崇.基于面元法及有限元法耦合的螺旋桨强度计算［J］.中国造船，2012，53（增刊1）：25-30.LIU Z Q，CHEN Y H，YAO Z C.Static strength analysis of civil ship propellers［J］.Shipbuilding of China，2012，53（Supp 1）：25-30（in Chinese）.

［12］苏玉民，黄胜.船舶螺旋桨理论［M］.哈尔滨：哈尔滨工程大学出版社，2003.

［13］肖翀，覃文洁，左正兴.曲轴应力场有限元计算单元类型和尺寸对计算精度和规模的影响［J］.柴油机，2004（S1）：176-178.XIAO C，QIN W J，ZUO Z X.Influence of elementform and element-size on FE calculation of crankshaft stress field［J］.Diesel Engine，2004（Supp 1）：176-178（in Chinese）.

［14］廖宏伟.基于迭代的六面体网格生成算法［D］.杭州：浙江大学，2013：20-34.LIAO H W.All-hexahedral mesh generation by iterative method［D］.Hangzhou：Zhejiang University，2013：20-34（in Chinese）.

［15］赵均海，汪梦甫.弹性力学及有限元［M］.武汉：武汉理工大学出版社，2003：18-20.

［16］苏玉民，黄胜.用面元法预报船舶螺旋桨的水动力性能［J］.哈尔滨工程大学学报，2001，22（2）：1-5.SU Y M，HUANG S.Prediction of hydrodynamic performance of marine propellers by surface panel method［J］.JournalofHarbin Engineering University，2001，22（2）：1-5（in Chinese）.

［17］胡健.螺旋桨空泡性能及低噪声螺旋桨设计研究［D］.哈尔滨：哈尔滨工程大学，2006.HU J.Research on propeller cavitation characteristics and low noise propeller design［D］.Harbin：Harbin Engineering University，2006（in Chinese）.

［18］王超.螺旋桨水动力性能、空泡及噪声性能的数值预报研究［D］.哈尔滨：哈尔滨工程大学，2010.WANG C.The research on performance of propeller's hydrodynamics，cavitation and noise［D］.Harbin：Harbin Engineering University，2010（in Chinese）.

［19］顾铖璋，郑百林.船用螺旋桨敞水性能与桨叶应力的数值分析［J］.力学季刊，2011，32（3）：440-443.GU C Z，ZHENG B L.Numerical analysis of propeller open-water performance and stress distribution in the blade of ship propeller［J］.Chinese Quarterly of Mechanics，2011，32（3）：440-443（in Chinese）.

［20］谭廷寿.非均匀流场中螺旋桨性能预报和理论设计研究［D］.武汉：武汉理工大学，2003.TAN T S.Performance prediction and theoretical design research on propeller in non-uniform flow［D］.Wuhan：Wuhan University of Technology，2003（in Chinese）.

Calculation of marine propeller static strength based on coupled BEM/FEM

YE Liyu，WANG Chao，LI Peng，WANG Xidong
College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China

U664.33

A

10.3969/j.issn.1673-3185.2017.05.008

2017-03-28< class="emphasis_bold">网络出版时间：

时间：2017-9-26 10:53

国家部委基金资助项目；国家自然科学基金资助项目（51679052）

叶礼裕，男，1989年生，博士生。研究方向：冰区船舶推进器设计及性能评估。E-mail：yeliyuxrxy@126.com

王超（通信作者），男，1981年生，博士，副教授。研究方向：舰船推进及减振降噪技术，冰区推进技术。E-mail：wangchao0104@hrbeu.edu.cn

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170926.1053.022.html期刊网址：www.ship-research.com

叶礼裕，王超，李鹏，等.BEM/FEM耦合螺旋桨静强度计算方法［J］.中国舰船研究，2017，12（5）：64-74，83.

YE L Y，WANG C，LI P，et al.Calculation of marine propeller static strength based on coupled BEM/FEM［J］.Chinese Journal of Ship Research，2017，12（5）：64-74，83.