一种距离模糊下三维空间高超声速弱目标HT-TBD算法
2017-10-13李岳峰王国宏张翔宇于洪波
李岳峰,王国宏,张翔宇,于洪波
(海军航空工程学院信息融合研究所,烟台264001)
一种距离模糊下三维空间高超声速弱目标HT-TBD算法
李岳峰,王国宏,张翔宇,于洪波
(海军航空工程学院信息融合研究所,烟台264001)
针对雷达测距模糊条件下临近空间高超声速弱目标的检测跟踪问题,提出一种基于分时多重频多假设的分级降维HT-TBD算法。首先,为重构因距离模糊而丢失的目标时空相关性,利用多种脉冲重复频率分时交替工作并对各时刻的距离模糊量测在所有多假设区间进行距离延拓;然后,为了在保证检测性能的同时减小计算量,将延拓后的三维点迹依次降维映射至径向距离-时间、方位角-时间和仰角-时间平面进行三级二维Hough变换,并在每级采用非相参积累和二值积累相结合的双重积累方式进行点迹筛选以在充分利用点迹能量信息的同时尽量减小强干扰的影响。仿真结果表明,该算法可在距离模糊条件下对临近空间高超声速弱目标进行有效检测跟踪,并同时实现距离解模糊。
临近空间;检测前跟踪;高超声速弱目标;三维Hough变换;距离模糊
0 引 言
临近空间为纵跨电离层和非电离层、距地面约20~100公里的空域。临近空间飞行器是以不低于5马赫的速度在临近空间内执行任务的飞行器[1-2]。临近空间飞行器的高超声速特性使其可在两小时内对全球任意目标实施打击;同时,高超声速运动产生的激波效应将明显减小目标的散射截面积(Radar cross-section, RCS),微弱的回波使目标具有较强隐身性,从而进一步增大探测难度。因此,关于临近空间高超声速弱目标的检测跟踪问题研究[3-6]对于国家空天安全具有重要影响。
检测前跟踪(Track-before-detect, TBD)技术是一种通过长时间积累实现微弱目标检测跟踪的有效技术。对目标多帧数据的非相参积累提高了目标航迹的信噪比(Signal-noise ratio, SNR),进而提升了对微弱目标的检测性能。现有的TBD技术主要包括投影变换方法[7]、三维匹配滤波器方法[8]、动态规划方法[9]、粒子滤波方法[10]等。其中,三维匹配滤波器方法与动态规划方法对低信噪比下的目标均具有较好检测性能,但当目标速度变化时,速度失配会造成计算量的明显增大与检测性能的下降;粒子滤波方法在处理非线性和非高斯问题上有显著优势,然而较高的计算复杂度限制了实际应用;投影变换方法通过降维映射大大减小了运算量,合理的投影方式亦可最大化地避免可能产生的噪声积累问题。基于Hough变换(Hough transform, HT)的TBD算法(HT-TBD)是一种典型的投影变换方法,它将数据空间的曲线检测问题转换成参数空间的峰值提取问题[11-13],具有对随机噪声鲁棒性强、对目标位置不确定性不敏感等优点,因此适用于强杂波环境。
近年来,国内外学者对常规目标HT-TBD算法展开了积极研究:文献[14]针对传统HT-TBD算法计算量大、航迹起始慢的问题,引入角度约束条件判断点迹是否共线,有效减少了虚假航迹;文献[15]为解决同一目标对应多条检测航迹的问题,提出一种基于相似航迹合并的HT-TBD算法,进一步精简了检测航迹。但上述算法只针对二维目标,未考虑目标仰角信息,不适应战场实际情况。对于三维目标,文献[16]在三维空间内直接进行三维Hough变换,产生的高维参数空间导致算法计算量过大,无法满足实际需要;文献[17]利用包含多普勒速度与斜距的量测信息,通过两个时间平面内的Hough变换起始目标航迹,进而解决三维空间目标的检测问题。
然而,上述研究只针对常规目标进行航迹检测并未考虑临近空间目标的特殊性,具有较大局限。考虑到临近空间目标距离较远,目标实际距离通常大于脉冲重复频率对应的最大不模糊距离,因此会产生距离量测模糊问题。对于测距模糊条件下的目标检测,文献[18]提出一种基于概率假设密度滤波的航迹起始算法,将距离模糊下的检测跟踪问题转换成混合状态滤波问题,对于多目标检测跟踪有较好效果;文献[19]采用Hough变换的思路,利用径向距离与时间信息,通过多重频条件下模糊距离与模糊数的联合估计,实现了在目标检测的同时解距离模糊。但是以上算法也只是针对二维目标检测,目前,作者尚未检索到将Hough变换用于测距模糊下三维临近空间目标检测的报道。
针对上述问题,本文在文献[19]的基础上提出一种基于分时多重频多假设的修正三级HT-TBD算法。相比上述研究,本文算法考虑了径向距离、方位角、仰角、能量、时间与目标运动信息,提升了信息利用率;将三维空间Hough变换分级降维成二维平面Hough变换的处理方式大大减小了计算量;三级时间平面的投影方式与双重积累方式提升了参数空间积累效率;航迹约束与归并有效减少了虚假航迹;分时多重频多假设的处理模式可以实现三维临近空间目标有效检测跟踪的同时解距离模糊。
1 问题描述
假设三坐标雷达位于坐标原点,目标为临近空间内做匀速直线运动的点目标,在运动过程中始终存在高斯白噪声过程扰动,雷达循环扫描周期为T,每次批处理N帧回波信号,则k时刻目标状态向量:
Xk=[rk,ϑk,φk,Sk]T
(1)
式中:rk,ϑk,φk分别为目标k时刻的径向距离、方位角和仰角坐标,Sk为目标回波功率值。因此,量测方程为
Zk=HXk+Wk
(2)
式中:Zk=[rk,ϑk,φk,Ek]T为k时刻量测向量,量测值为真实值与量测误差之和,即rk=rreal+dr,ϑk=ϑreal+dϑ,φk=φreal+dφ,量侧误差dr、dϑ、dφ均服从零均值正态分布。Ek为回波功率量测值,Wk为量测噪声,量测矩阵H为四阶单位阵。
(3)
式中:Nk(rk,ϑk,φk)表示k时刻(rk,ϑk,φk)点零均值高斯白噪声功率值,Sk(rk,ϑk,φk)表示k时刻目标点(rk,ϑk,φk)的功率值,根据雷达方程[20]:

(4)
式中:Pt为发射功率,G为发射增益,σ为目标散射截面积,λt为发射波长,R为径向距离。
测距作为雷达的基本功能之一是通过测量回波相对发射脉冲的时延来实现的。作为雷达常用的工作模式,高脉冲重复频率(PRF)工作模式具有良好的速度分辨力。但是较小的脉冲重复周期Tr使得目标的真实回波时延τtrue大于脉冲重复周期Tr,如图1所示,由于脉冲是连续发射延迟接收,很难确定回波E1的原始发射脉冲是P1到P3中的哪一个,因此存在测距模糊现象。通常默认回波脉冲E1源于最近的发射脉冲P3,进而获得模糊时延:
τamb=mod[τtrue,Tr]
(5)
式中:mod[A,B]表示A对B取余。

图1 高PRF模式下雷达测距原理图Fig.1 Schematic of radar ranging under high PRF pattern

(6)
2 算法原理
本文算法从结构上主要分成两部分:距离模糊条件下的多假设映射处理以及三维空间分级降维HT-TBD算法,算法处理流程如图2所示。
由于距离雷达较远,临近空间目标往往会出现目标距离大于雷达重频对应最大不模糊距离的情况,从而产生距离模糊现象,破坏目标量测时空连续性与相关性,为后续积累检测带来困难。同时,一方面由于临近空间目标回波微弱,较难利用传统的余数定理法在同一时刻有效获得多个重频的回波信号用于解模糊;另一方面,由于临近空间目标运动速度很快,若利用传统的余数定理法解模糊可能出现某一时刻发射多重频脉冲期间目标运动跨越距离模糊区间的情况,因此传统的多重频解距离模糊的方法不适用于临近空间目标。
为实现距离模糊条件下对于临近空间高超声速弱目标的有效检测跟踪,考虑到无测距误差时实际距离与模糊距离的差值必定是雷达重频对应最大不模糊距离的整数倍,本文算法采用不同脉冲重复频率分时交替工作的方式,利用距离多假设的思想将所有量测点依次映射至各个多假设距离空间。由于多假设处理后只有目标实际量测点才满足目标运动特性从而可以进行有效积累,因此,对于扩展后的量测点利用提出的分级降维HT-TBD算法能够实现有效检测跟踪,并且可以同时达到距离解模糊的目的。
为了在降低三维Hough变换因高维参数空间而产生的大计算量的同时减小噪声积累和远距离条件下角度偏差引起的较大横向误差的不利影响,分级降维HT-TBD算法将依次把三维空间量测点投影至距离-时间、方位角-时间、仰角-时间平面进行三级检测,通过逐级二维Hough变换筛选目标点迹,以最大限度提升算法精度;为了在充分利用能量信息提升积累效率的同时,尽可能减小强干扰的影响,从而有效避免二进制积累方式的明显缺陷,分级降维HT-TBD算法并行采用非相参积累和二值积累相结合的双重积累方式;同时,引入速度、角度和加速度的多种运动约束及航迹归并措施,进一步减少了虚假航迹数。

图2 算法总体流程图Fig.2 Overview flow chart of the algorithm
2.1距离模糊条件下分时多重频多假设映射处理



图3 距离模糊原理剖面图Fig.3 Profile map of range ambiguity principle
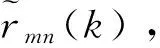

(8)


(9)



(10)
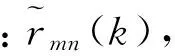
zmn(k)={rmn(k),ϑmn(k),φmn(k),Smn(k)}
(11)
式中:映射处理后距离rmn(k)如式(8)所示,包含所有可能多假设距离延拓值。由于所有扩展量测中只有真实航迹中的量测点迹满足原始时空相关性,因此可以利用后续分级降维HT-TBD算法通过积累检测的方式挖掘出三维空间的潜在目标航迹,同时实现距离解模糊。
2.2分级降维HT-TBD算法
在多假设映射处理的基础上,针对临近空间内多重距离延拓后的量测点迹,考虑到HT-TBD算法具有对随机噪声鲁棒性强、对目标位置不确定性及局部缺损不敏感等优点,采用HT-TBD算法实现距离模糊下临近空间高超声速目标的检测跟踪。
为了在减小数据处理量的同时尽可能保留目标量测,本文在较高虚警率下设置较低初始门限,仅对过门限量测点进行三级Hough变换点迹筛选。由于三级变换的基本流程类似,仅以第一级为例阐述。
第一级Hough变换在映射后的径向距离-时间平面进行,并通过式(12)将t-r平面的数据点变换到参数空间Ω1:
ρ=tcosθ+rsinθ
(12)
式中:ρ为量测点所在直线与原点的垂线距离,θ为该垂线与横轴正方向的夹角。
由于数据空间中的共线点迹对应参数空间中一簇正弦曲线的交点(ρ0,θ0),因此,可以通过提取峰值参数(ρ0,θ0)将数据空间内的对应直线检测出来。

(13)
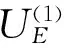
由于实际每帧数据只存在一个目标点,为提升积累效率,避免大量杂波点的无效积累湮没目标航迹积累值,算法将按照以下两项原则进行双重积累:

(14)
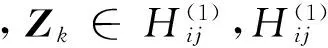

(15)


在利用目标点的时空相关性通过三级Hough变换筛选出真实目标点迹的基础上,通过进一步引入航迹速度、角度和加速度约束以及相似航迹归并进一步对航迹进行精简,有效减少虚假航迹数,提升算法性能。根据式(9),可解出模糊量测点在各重频下所对应的唯一脉冲间隔数,从而在检测出目标点迹的同时实现距离解模糊。
3 仿真校验
3.1参数设置

本文仿真试验平台为ASUS TW100-E5工作站(CPU: Intel core II,主频: 2.6GHz,内存: 4GB),仿真软件为Matlab 2010a,并采用航迹检测概率Pd、航迹虚警概率Pf和平均运行时间Trun三项指标来评估算法性能:
(16)
式中:M为蒙特卡洛试验次数,εi为逻辑变量,若在第i次试验中检测到目标,εi赋1,否则置0。

(17)
式中:fi为第i次试验检测到的虚假航迹数;Fi为在第i次试验检测到的航迹总数。
(18)
式中:ti表示第i次试验算法运行时间。
3.2仿真结果与分析
为全面验证本文算法的有效性,本文从目标运动跨距离模糊区间情况、不同信噪比、不同杂波密度三个方面进行仿真验证,并在测距模糊条件下与文献[16]、文献[17]和文献[19]中的3种HT-TBD算法进行检测性能的比较。3.2.1 目标运动跨距离模糊区间情况下的算法性能
为检验目标跨距离模糊区间运动对算法性能的影响,在信噪比等于6 dB、杂波密度λc=400条件下在上述参数设置的基础上进行仿真试验,并与文献[16]、文献[17](利用单重频f=1.75 kHz检测)和文献[19]算法进行检测性能比较。易知,此时7帧目标的运动点迹跨越距离模糊区间,由于量测误差的引入,临近空间目标量测已与标准直线有不小偏差,线性弱化的目标航迹增大了检测难度。无距离模糊真实三维量测、模糊三维量测与多假设处理后的扩展量测点迹分别如图4(a)~(c)所示。
当目标跨距离模糊区间运动时,由图4(b)可知,折叠后雷达最大不模糊区间内的目标量测点已失去原有的特定时空相关性,此时目标点迹完全偏离直线,很难直接利用HT-TBD方法检测出目标。

图4 三维量测分布图Fig.4 Three-dimensional measurement point distribution
为实现对临近空间目标的有效检测,采用第2.1节的分时多重频多假设的方法将模糊量测映射至各个多假设区间,如图4(c)所示,经过第2.2节的分级降维HT-TBD算法,最终检测出目标点迹,如图5所示。由式(8)可知,多重频分时交替延拓后的量测点中必然包括所有真实目标量测,可在三维空间积累检测出真实航迹;而对于在其他多假设区间内的扩展目标点迹,由于各时刻重频的差异性,后续映射至径向距离-时间平面的各帧目标扩展量测点的相对位置发生改变,无法通过分级降维HT-TBD积累到一条直线。因此,本文算法可以有效检测出大部分真实目标量测点。
在分级降维HT-TBD中,本文采用点数、能量双重积累方式将数据空间映射到参数空间进行峰值提取,三级积累结果如图6所示。经过三级Hough变换点迹筛选,杂波点被逐级剔除,积累峰值也愈发显著,如图6(c)和6(f)所示,第三级双重积累直方图的峰值已经十分尖锐,算法筛选效果较好,可以有效提取对应参数单元峰值点参数并进行回溯。
最终,算法可以实现在目标检测的同时解距离模糊。当雷达采用上述3种脉冲重复频率分时交替工作时,由式(9)计算可得,目标量测点所对应的脉冲间隔数qm分别为q1=3,q2=4,q3=6。
分别经过500次蒙特卡洛仿真试验的上述4种算法检测性能如表1所示。
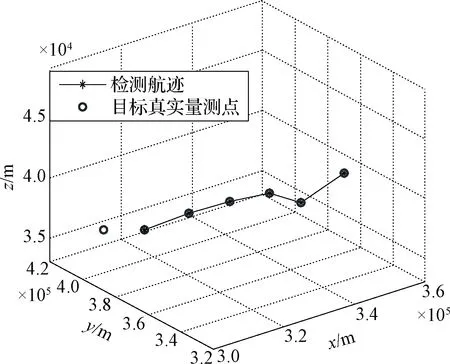
图5 算法最终检测航迹Fig.5 Final detected trajectory

图6 三级Hough变换双重积累直方图Fig.6 Double accumulation model histogram of three-stage Hough transform

评估指标PdPfTrun/s本文算法0.810.429.89文献[16]0.290.9157.36文献[17]0.220.956.21文献[19]0.610.628.67
当目标运动跨模糊区间时,原始的不模糊目标点迹经过折叠丧失了原有航迹连续性,因此难以利用文献[16]和文献[17]的算法直接检测出目标,加之未利用能量信息且未进行航迹检验,航迹虚警概率均在90%以上;文献[19]利用多重频的方法进行解模糊,能够估计出真实目标点位置,但由于只利用了距离、时间信息,检测性能受到制约,检测概率维持在60%左右;本文算法将量测点迹进行多假设延拓,可恢复出所有目标点真实位置,从而利用目标时空相关性检测出目标量测点迹,信息利用率的提升以及航迹约束与航迹归并的引入使得检测概率可达80%以上,航迹虚警概率也远小于其他3种算法。在运行时间方面,针对三维目标的文献[16]算法因5维参数空间的构建耗费了大量运算资源,运行用时高达约1分钟,无法用于实际;文献[17]在单重频条件下由于未设置合适初始门限相对多重频延拓算法未在计算用时上体现出明显优势;在多重频解模糊框架下,采用三级二维Hough变换结构的本文算法相比采用单级二维Hough变换的文献[19]算法运行用时增长约14%。综上所述,本文算法相对其他3种算法具有更优检测性能,在解距离模糊的基础上,计算量的适度增加是可以接受的。
3.2.2 不同信噪比对算法性能的影响
为进一步分析不同信噪比下算法的检测性能,对于同一目标在参数设置不变的条件下,针对不同信噪比各进行500次蒙特卡洛仿真试验,并与上述3种算法对比分析,相应检测概率曲线如图7所示。

图7 不同信噪比条件下的检测概率比较Fig.7 Detection probability comparison under different SNR
由图7可知,4种算法的检测概率均随信噪比的升高而增大。由于此时目标运动跨距离模糊区间,个别跨模糊区间的目标点迹在折叠后已经与其他模糊目标量测点完全失去线性关联性,从而导致仅利用单重频信号的文献[16]与文献[17]算法的检测概率大幅下降,始终处于50%以下,基本无法进行有效检测;文献[16]算法相对文献[17]算法由于多利用了高度维信息,因此检测概率稍高。在多重频解距离模糊框架下,目标运动是否跨模糊区间并不影响检测,因此本文算法与文献[19]算法在大多数情况下均可检测到目标航迹;由于多利用了方位角、仰角信息,本文算法相比文献[19]算法检测概率有较为明显的提升。当信噪比大于10 dB时,过初始门限干扰点较少,本文算法与文献[19]算法的检测概率超过90%;随着信噪比的降低,过门限干扰点逐渐增多,检测概率下降较为明显,当信噪比小于4 dB时,本文算法检测概率降到50%以下,文献[19]算法的检测概率则降至30%以下。综上所述,不同信噪比条件下,本文算法的检测概率明显优于其他3种算法;当信噪比较高时,本文算法对于距离模糊条件下临近空间高超声速弱目标具有较好检测能力。
3.2.3 不同杂波密度对算法性能的影响
为进一步验证不同杂波密度下本文算法的有效性,在信噪比等于6 dB且参数设置不变的条件下,对同一目标针对不同杂波密度各进行500次蒙特卡洛仿真试验,并通过与上述3种算法检测性能的对比分析体现本文算法优越性,仿真结果如表2所示。

表2 不同杂波密度下检测性能比较Table 2 Comparison of detection performance under different clutter density
从表2可以看出:
1) 4种算法的航迹检测概率均随杂波密度λc的增加而降低。由于跨模糊区间的目标运动破坏了折叠后第一模糊区间内目标点迹的连续性,未解距离模糊的文献[16]与文献[17]算法的检测概率始终处于50%以下,明显低于可以实现解模糊的本文算法与文献[19]算法;文献[19]算法由于较低的信息利用率,检测概率与本文算法相比仍有一定差距,当λc=100时,本文算法的检测概率可达90%以上;随着杂波密度的增加,文献[19]算法相比本文算法检测概率下降更为明显,因此对杂波密度更加敏感。
2) 4种算法的航迹虚警概率均随杂波密度λc的增加而升高。跨模糊区间运动的目标点迹使得所有目标点无法在参数空间积累到同一单元,加大了峰值提取难度,使得文献[16]与文献[17]算法更易引发航迹误判,虚警率始终高于65%;文献[17]算法相比文献[16]算法由于未利用仰角信息,检测效果进一步降低;本文算法与文献[19]算法由于实现了距离解模糊具有明显较低的虚警率,三级点迹筛选的引入以及多条件航迹约束与航迹归并措施剔除了大部分杂波点,使本文算法的虚假航迹数大大降低,当λc=700时,本文算法的航迹虚警率Pf仅为文献[19]算法的69%,文献[17]算法的57%。
3) 4种算法的运行时间均随杂波密度的增加而延长。由于高维参数空间的构建,文献[16]算法耗时明显高于其他算法并且随着杂波密度的增加,运行时间上升最为明显,当λc=700时,运行时长已增加至其它算法的4倍以上。单重频条件下采用两级二维Hough变换的文献[17]算法用时最短,但由于未设置合适初始门限相对多重频延拓算法未在计算用时上体现出明显优势。在多重频解模糊框架下,多假设点迹延拓以及多级Hough变换的引入使得本文算法相对文献[19]算法用时更长;当杂波密度λc较低时,过初始门限点迹较少,因此多级Hough的引入不会额外增加过多计算量,二者用时相近;随着杂波密度的增大,多假设处理后的延拓点迹成倍增加,各级Hough变换处理点迹也越来越多,相比采用单级二维Hough变换的文献[19]算法,此时本文算法计算量有较为明显的增加,当λc=700时,运行用时增长约20%。因此,测距模糊条件下本文算法的良好检测性能是以增加计算量为代价的。
在实际应用中,为进一步加快HT-TBD算法对高超声速目标检测的运行速度,可以采用硬件加速的实现方式,从而大大缩短算法实际运行时间并可基本满足实际需要。此外,关于HT-TBD的各种快速实现算法(例如递推、并行的处理方式)也可达到算法加速的目的,有待后续进一步的深入研究。
4 结 论
为解决测距模糊条件下雷达对临近空间高超声速弱目标的检测跟踪问题,提出一种基于分时多重频多假设的分级降维HT-TBD算法。该方法通过将距离模糊量测映射至不同重频下的多个距离假设区间提取真实目标点的时空相关性,从而在实现检测跟踪的同时解距离模糊。为提升三维空间航迹检测性能,在三个时间平面内依次进行三级Hough变换点迹筛选,并采用非相参积累和二值积累相结合的双重积累方式提升积累效果。与现有HT-TBD算法相比,在距离模糊条件下本文算法检测性能更佳,并可同时实现距离解模糊,具有一定工程实践意义。
[1] Zhang J M, Sun C Y, Zhang R M, et al. Adaptive sliding mode control for re-entry attitude of near space hypersonic vehicle based on backstepping design[J]. IEEE/CAA Journal of Automatica Sinica, 2015, 2(1): 94-101.
[2] 张翔宇, 王国宏, 宋振宇,等. LFM雷达对临近空间高超声速目标的跟踪研究[J]. 电子学报, 2016, 44(4): 846-853. [Zhang Xiang-yu, Wang Guo-hong, Song Zhen-yu, et al. Tracking of hypersonic target in near-space with LFM radar[J]. Acta Electronica Sinica, 2016, 44(4): 846-853.]
[3] Zhu S Q, Liao G S, Yang D, et al. A new method for radar high-speed maneuvering weak target detection and imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1175-1179.
[4] Mu C X, Ni Z, Sun C Y, et al. Air-breathing hypersonic vehicle tracking control based on adaptive dynamic programming[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(3): 584-598.
[5] 李林, 王国宏, 于洪波,等. 一种临近空间高超声速目标检测前跟踪算法[J]. 宇航学报, 2017, 38(4): 420-427. [Li Lin, Wang Guo-hong, Yu Hong-bo, et al. A TBD algorithm for near space hypersonic target[J]. Journal of Astronautics, 2017, 38(4): 420-427.]
[6] 翟岱亮, 雷虎民, 李炯,等. 基于自适应IMM的高超声速飞行器轨迹预测[J]. 航空学报, 2016, 37(11): 3466-3475. [Zhai Dai-liang, Lei Hu-min, Li Jiong, et al. Trajectory prediction of hypersonic vehicle based on adaptive IMM[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3466-3475.]
[7] Yu H, Wang G H, Wu W, et al. A novel RHT-TBD approach for weak targets in HPRF radar[J]. Science China Information Series, 2016, 59(12): 1-14.
[8] Kennedy H L. Efficient velocity filter implementa-tions for dim target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2991-2999.
[9] Zhang D, Wang S, Meng Q. Dynamic programming track-before-detect algorithm for radar target detection based on polynomial time series prediction[J]. IET Radar, Sonar & Navigation, 2016, 10(8): 1327-1336.
[10] Garcia-fernandez A F. Track-before-detect labeled multi-bernoulli particle filter with label switching[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(5): 2123-2138.
[11] Carson B D, Evans E D, Wilson S L. Search radar detection and track with the Hough transform part I: system concept[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 102-108.
[12] Carson B D, Evans E D, Wilson S L. Search radar detection and track with the Hough transform part II: detection statistics[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 109-115.
[13] Carson B D, Evans E D, Wilson S L. Search radar detection and track with the Hough transform part III: detection performance with binary integration[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 116-125.
[14] Chen J, Henry L, Tiyus L, et al. A modified probabilistic data association filter in a real clutter environment[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 300-313.
[15] 王国宏, 李林, 于洪波. 基于点集合并的修正Hough变换TBD算法[J]. 航空学报, 2017, 38(1): 203-213. [Wang Guo-hong, Li Lin, Yu Hong-bo. A modified Hough transform TBD algorithm based on point set merging[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 203-213.]
[16] Moqiseh A, Nayebi M M. 3-D Hough transform for surveillance radar target detection[C]. Proceedings of IEEE Radar Conference, Rome, Italy, May 26-30, 2008.
[17] 金术玲, 梁彦, 王增福,等. 两级Hough变换航迹起始算法[J]. 电子学报, 2008, 36(3): 590-593. [Jin Shu-ling, Liang Yan, Wang Zeng-fu, et al. A two-hierarchy Hough transform based track initiation algorithm[J]. Acta Electronica Sinica, 2008, 36(3): 590-593.]
[18] Tan S C, Wang G H, Yu H B. Joint range ambiguity resolving and multiple maneuvering targets tracking in clutter via MMPH-DF-DA[J]. Science China Information Series, 2014, 57(8): 1-12.
[19] Li L, Wang G H, Zhang X Y, et al. A TBD algorithm for near space hypersonic target under the condition of range ambiguity[C]. The 2nd IEEE International Conference on Computer and Communication, Chengdu, China, October 14-17, 2016.
[20] Mark A R, James A S, William A H.Principles of modern radar[M]. Edison,New Jersey: Science Technology Publishing, 2010.
AHoughTransformTBDAlgorithminThree-DimensionalSpaceforHypersonicWeakTargetunderRangeAmbiguity
LI Yue-feng, WANG Guo-hong, ZHANG Xiang-yu, YU Hong-bo
(Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China)
To address the problem of detection and tracking for the near-space hypersonic weak targets under range ambiguity, a novel hierarchical and dimension-decreasing Hough transform track-before-detect (TBD) algorithm is proposed based on the multiple pulse repetition frequencies (PRF) and range multi-hypothesis processing with time-sharing. Firstly, to rebuild the lost space-time relativity of the target points under range ambiguity, different PRFs are utilized alternately at different times and measurements with range ambiguity are extended to all range multi-hypothesis intervals. Then, the three-dimensional measurements after range extension are mapped into the range-time plane, azimuth-time plane and elevation-time plane by turns before two-dimensional Hough transform in each plane to ensure the great detection performance and decrease the calculation load. In addition, point selection is conducted by the double integration means of the non-coherent integration and binary integration to decrease the impact from the strong interference and utilize the energy information of points simultaneously. Simulation results demonstrate the effectiveness of the proposed algorithm.
Near space;Track-before-detect;Hypersonic weak target;Three-dimensional Hough transform; Range ambiguity
V243.2; TN957
A
1000-1328(2017)09- 0979- 10
10.3873/j.issn.1000-1328.2017.09.011
2017- 04- 18;
2017- 07- 06
国家自然科学基金(61731023,61372027,61501489,61671462,61701519); “泰山学者”建设工程专项经费资助项目
李岳峰(1992-),男,博士生,主要从事机动目标检测与跟踪等方面的研究。
通信地址:山东省烟台市二马路118号海军航空工程学院信息融合研究所(264001) 电话:15506591185 E-mail:liyuefeng1992@126.com
