基于树结构的本体概念相似度计算方法①
2017-10-13徐英卓
徐英卓, 贾 欢
基于树结构的本体概念相似度计算方法①
徐英卓, 贾 欢
(西安石油大学计算机学院, 西安 790065)
随着本体在数据集成方面的广泛应用, 面向本体的概念相似度计算成为人们关注的热点问题. 针对当前领域本体概念相似度的计算过程都比较复杂的问题, 提出一种基于树结构的本体概念相似度的计算方法. 该方法通过添加和重组虚拟节点重构本体树, 再通过属性比较映射对象, 最后通过计算, 得到本体概念的语义相似度结果. 实验结果表明, 该方法有效利用了本体概念的语义信息, 得到了合理的计算结果, 并简化了计算过程.
本体; 概念相似度; 树结构
数据集成的一个难点是分布式语义信息集成, 在语义集成方面, 可以将数据集成看作是一个知识表示问题. 然而, 相同的知识经常使用不同的本体来表达, 不同的应用之间对相同知识的表达也不相同[1], 结果就会产生误解和冲突. 因此, 建立本体映射来加强可理解性, 从而有效地解决这种冲突是非常必要的[2]. 语义集成的关键是本体映射, 而本体映射的关键是概念相似度计算. 当前概念相似度计算方法大致可分为两类: 一类利用大规模语料库进行统计, 依据词汇上下文信息的概率分布进行计算, 这种方法比较精准, 但是需要依赖于训练所用的语料库, 计算量大且易受训练数据噪声影响; 另一类基于某种世界知识来计算, 主要是基于某个知识完备的语义词典中的层次结构关系进行计算, 这种方法比较直观, 易受人们的主观意识影响[3,4]. 中科院刘群的基于《知网》的词语相似度计算是当前比较有代表性的计算概念相似度的方法之一.
很多学者考虑到其他因素对概念相似度的影响, 如黄果等人[3]提出的以基于距离的计算模型为基础, 把概念的信息内容和概念的属性作为两个决策因子来计算相似度的方法, 能较准确地反映概念之间的语义关系, 但是计算过程复杂; 刘紫玉等人[5]在本体模型的基础上提出领域本体模型的八元组表示方法和领域
表示方法, 给出领域本体模型的有向循环图, 通过综合计算, 得到领域本体中概念的实际相似度, 能够比较准确地反映概念之间的语义关系, 但是计算量比较大; 姜华[6]提出的改进的本体语义相似度计算方法, 该方法考虑了本体结构中概念的共同分离祖先和几种语义距离影响因子, 将信息量融合到语义距离的计算中, 得到了较合理的实验结果, 但是计算范围较小. 本文提出一种基于树结构的概念语义相似度计算方法, 该方法根据本体概念的特点及概念间的关系, 利用树结构的层次特点计算基于实例的概念相似度, 能发掘更多的潜在信息, 提高计算的准确性, 简化计算过程, 并通过实验对所提方法进行了实验验证.
1 基于树结构的本体概念相似度算法
概念相似度是指两个概念之间的相似程度, 通常指两个概念间具有某些共同特性[7]. 本文用树形结构模拟本体, 并用树结构表示所有的节点关系, 每个节点代表一个概念[8]. 本节将详细阐述一种重组方法, 利用中间本体树和源本体树通过增加和组合虚拟节点来规范所有的树结构, 并利用本体映射关系进行概念相似度的计算.
假设所有的本体信息使用XML和XML DTD表示, 本文提出的本体概念相似度算法包括本体模型的构建和本体概念相似度计算两部分.
1.1 本体模型的构建
1.1.1将XML转换为树结构
假设有本体O, 其根节点为A, I(A, B)表示B继承于A, I’(A, B)表示A和B是兄弟节点. 那么, 创建本体树的关联规则如下[9]:
I(C, B)^ I(B, A)àI(C, A)
I(A, B)^ I(B, C)à I(A, C)
I(A, B)^ I(C, A)à I(C, B)
I(A, B)^ I(A, C)à I(B, C), I’(B, C)
分类元素并建立本体树: 当元素不在DTD文件的末端时, 如果一个元素X有子元素, 那么将X作为子元素的一个父元素记录下来, 否则, 将X作为根节点; 如果元素X有一个父元素Y, 那么将X作为Y下面的节点, 否则, 将X作为Y的一个属性值. 再到下一个元素, 如此循环.
1.1.2重构本体树
本体树由不同的DTD表达模式转换而来, 其多样性使得它很难进行本体映射[10], 因此可以借助于中间本体树完成映射过程. 重构本体树的过程包括三个步骤: 特征提取、匹配识别和结构比较.
1) 特征提取
从待映射的本体中获取特征值, 包括本体中的概念集合、属性集合等, 通过比较属性集合进行本体匹配映射. 若两个属性集包含的属性数目相同, 属性名称相似, 且数据类型相同, 则它们是等价属性集; 若两个属性集的数量相同且属性内容相似, 则它们是等效属性集; 若两个对象是兄弟节点, 且有一个等效属性集, 则可从中提取这些等价属性组合成的新属性设置为其共同的父对象.
2) 匹配识别
根据提取的属性特征, 对待映射的本体进行匹配. 若两个对象都是叶子节点, 且拥有相同的属性集, 则它们是精确匹配的; 若只有部分属性匹配, 则它们是部分匹配的. 对于非叶子节点, 可以用它们的子节点进行匹配. 若所有的属性和子节点都是精确匹配, 则这两个非叶子节点也是精确匹配. 若它们的属性是部分匹配, 并且部分匹配的子节点数目相同, 则它们也是部分匹配的.
3) 结构比较
通过创建虚拟节点重构中间本体树和源本体树. 此过程以已经确定的精确匹配或部分匹配的节点开始. 例如下图中所示, 图1给出了钻井作业中间本体树, 图2给出了钻井作业源本体树.
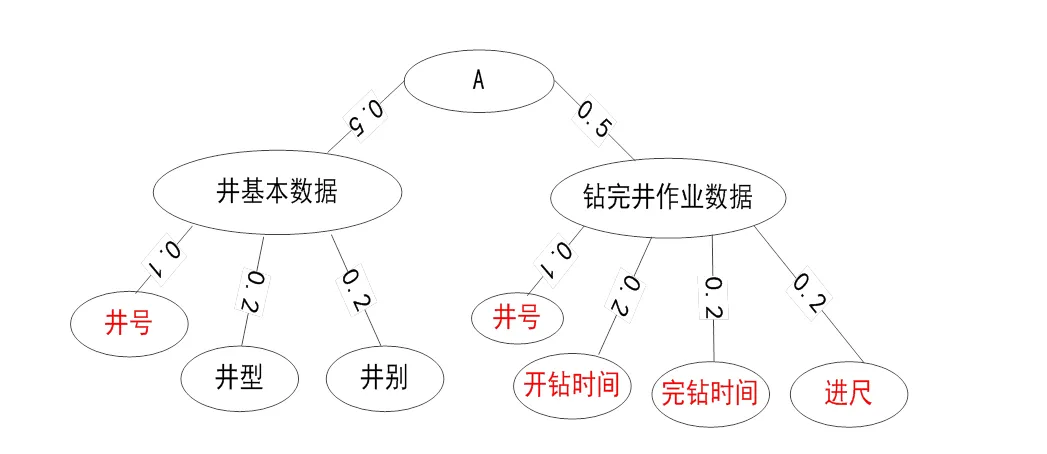
图1 钻井作业中间本体树(部分)
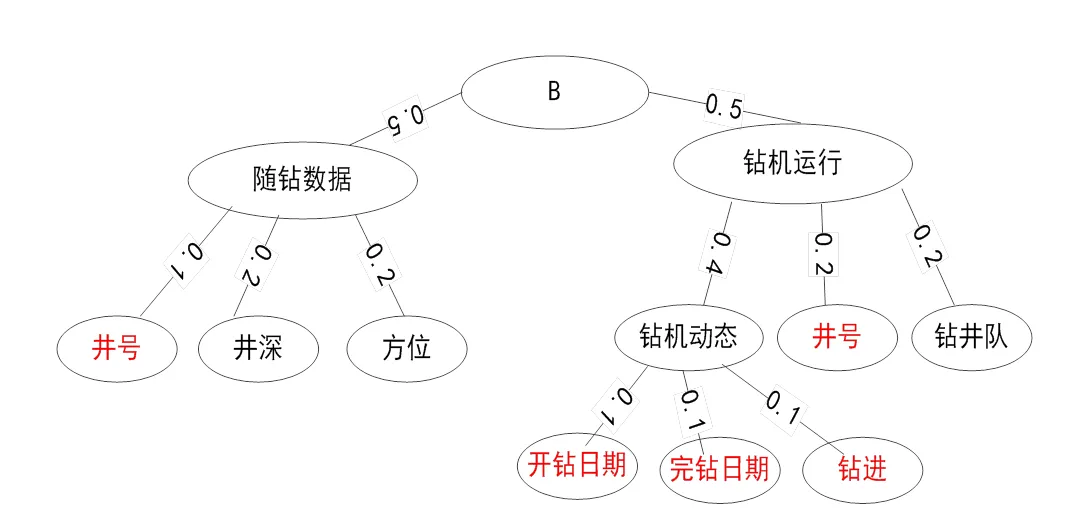
图1 钻井作业源本体树(部分)
假设可以找到以下精确/部分匹配对:
① 井号(A)à井号(B)
② 开钻时间(A)à开钻日期(B)
③ 完钻时间(A)à完钻日期(B)
④ 进尺(A)à钻进(B)
对每一个匹配对进行绝对位置计算, 绝对位置是节点与根节点之间的距离[11]. 如果将根节点定义为0级(level 0), 那么节点的绝对位置就等于节点的级别.
① 井号(A) level 2à井号(B) level 2
② 开钻时间(A) level 2à开钻日期(B) level 3
③ 完钻时间(A) level 2à完钻日期(B) level 3
④ 进尺(A) level 2à钻进(B) level 3
定义1. 设X、Y是本体树中的任意两个节点, Level(X)表示节点X所处的层级, Level(Y)表示节点Y所处的层级, |Level(X)- Level(Y)|表示节点X和节点Y的层级差.
后面三个匹配对在不同的层级, 结果表明中间本体树与源本体树之间的结构是不同的, 应该向具有较低绝对位置的树添加虚拟节点. |Level(X)- Level(Y)|的值表示需要添加的虚拟节点数. 如果具有较低绝对位置的节点N处在1级, 那么应该为这个绝对位置N添加虚拟父节点, 否则, 进一步执行比较程序为虚拟节点找到合适的位置. 虚拟节点插入程序应该被执行|Level(X)- Level(Y)|次, 计算节点X和节点Y的部分匹配子节点数目. 如果节点X是部分匹配节点, 而它的子节点数目和其他任何部分匹配节点的子节点数目都不相同时, 那么添加的虚拟节点和X的子节点在同一层级, 新增加的节点以节点X和其兄弟节点的名字命名, 其名称表明了它们的功能.
1.2 本体概念相似度计算
1.2.1基本定义
定义2. “本体概念相似度”是描述两个词语在文章上下文结构中可以相互替换使用而不改变文本的句法、语义结构的程度. 其应用也十分广泛, 从心理学、语言学、认知科学到人工智能都有涉及[12].
概念相似度是一个数值, 取值范围为[0, 1], 一个词语和它本身的相似度是1(相同) , 如果两个词语在任何上下文中都不可替换, 则它们的相似度为零[13].
定义3. “边权值”表示连接两个节点的路径上的值, 也可以理解为结点间的距离.
假设各条边的边权值相等, 则在语义距离相等的情况下, 距离根节点远的概念间的相似度要比距离根节点近的概念间的相似度高. 因此, 边权值的大小应该随其在本体树中所处的深度不同而变化. 我们设定深度越深, 边权值越小, 每个节点的边权值为该节点流出的边权值和流入的边权值之和, 根节点的边权值为1.
定义 4. 如果领域本体中概念S和S成同义关系, 即可以相互替换而不影响文字所表达的意思, 那么概念S和 S的相似度为1, 可以用公式表示为.
根据“知网”[15], “概念”是对词汇语义的一种描述. 每一个词可以表达为几个概念. “概念”是用一种“知识表示语言”来描述的, 这种“知识表示语言”所用的“词汇”叫做“义原”. “义原”是用于描述一个“概念”的最小意义单位.
1.2.2算法描述
目前, 计算概念相似度的方法多数是基于文献[14]提出的方法, 在计算两个概念的相似度时, 通过计算其所在层次树上的最短路径距离Sim来确定其相似度, 如公式(1)所示:
从公式(1)可以看出,的值越小, 两个概念之间距离越近,值越大, 其相似度也越大. 由此可知, 一个概念的兄弟节点就是与其相似度最高的概念节点.
该方法只考虑了路径距离, 没有考虑其他因素, 得出的结果在一定程度上与人的正常逻辑思维不符合[14], 例如, “汽车”和“自行车”两个词语, 在语义方面都是表示一种交通工具, 从主观上来看相似度很高, 但是利用文献[14]的方法计算的到的相似度并不是很高. 因此本文提出一种新的方法, 考虑不同概念在本体树中所占的比重不同, 给其加上合理的边权值, 在一定程度上削弱距离对相似度值的影响, 使得计算结果更符合人们的主观认识.
由此, 根据以上映射规则, 在领域本体中, 对于两个概念S和S, 提出相似度计算公式为:
1.2.3整体计算步骤
根据上面1.1节形成的映射关系, 对本体概念相似度计算可分为两个步骤进行: 1)比较本体概念所处的层级, 重构本体树; 2)概念相似度值的具体计算.
具体计算流程如图3所示.
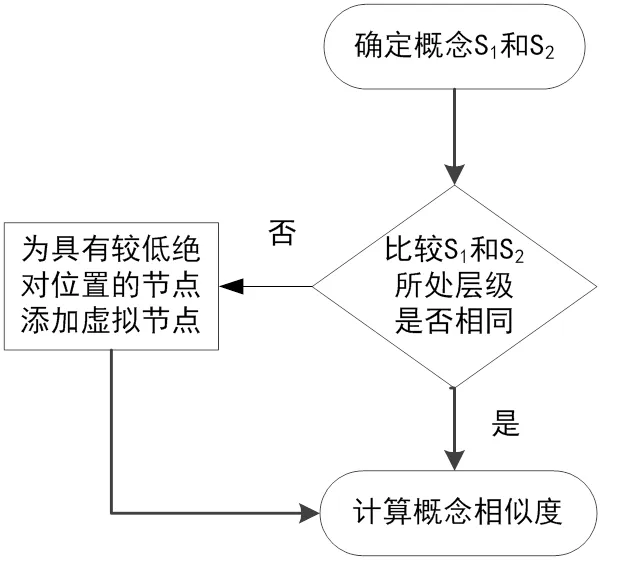
图3 计算流程图
整体计算步骤如下:
步骤1: 构建本体树, 找到所有的概念匹配对.
步骤2: 比较两个概念所处的层级是否相同, 如果二者在处于同一层级, 那么可以直接进行概念相似度计算, 否则执行下一步操作.
步骤3: 为具有较低绝对位置的节点添加虚拟节点, 然后进行概念相似度计算.
步骤4: 利用公式(2)进行相似度的计算, 通过相似度的值判断两个概念的相似程度.
2 实例验证
本实验构建了钻井作业本体树如图4, 以图1和图2所示钻井本体片段为例, 选择具有代表性的概念进行相似度计算, 图中的概念用Si表示. 根据以上方法, 本文实现了一个基于树结构的语义相似度计算模型.
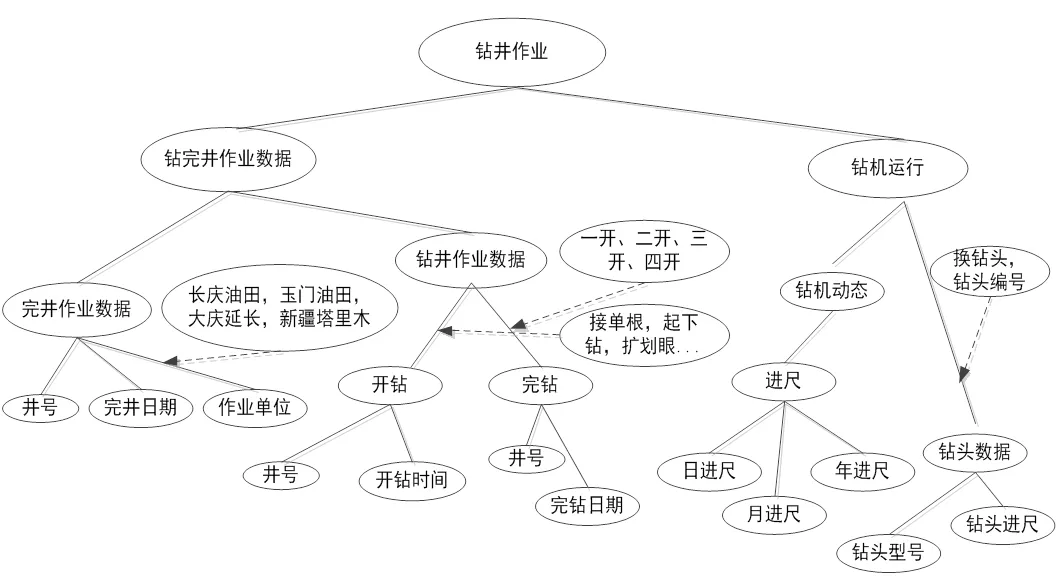
图4 钻井作业本体树
例如: 计算“进尺”和“钻进”这两个概念的相似度值时, 由于节点“钻进”处于较低绝对位置, 所以需要为其在本体树中添加虚拟节点, 虚拟节点线框及连接线用虚拟线条表示, 得到新的结果本体树O, 如图5所示, 图中带箭头的虚线表示匹配关系.
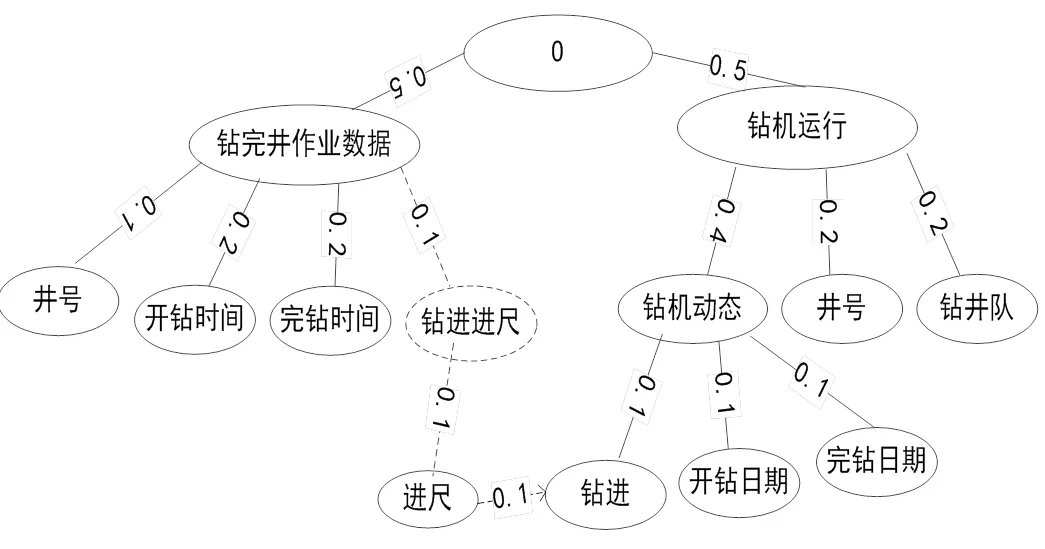
图5 结果本体树(部分)
计算“钻进&进尺”匹配对的相似度值, 根据计算公式,=0.1,1, 当=0.02,Sim(钻进, 进尺)= 0.882.
对于本体概念相似度计算的结果评价, 本文采用了人工判别的方法. 为了验证方法的有效性, 使用两种方法实现概念的相似度计算, 并对它们的计算结果进行比较. 方法1采用基于《知网》的语义相似度计算方法[16], 方法2采用本文提出的语义相似度计算方法.
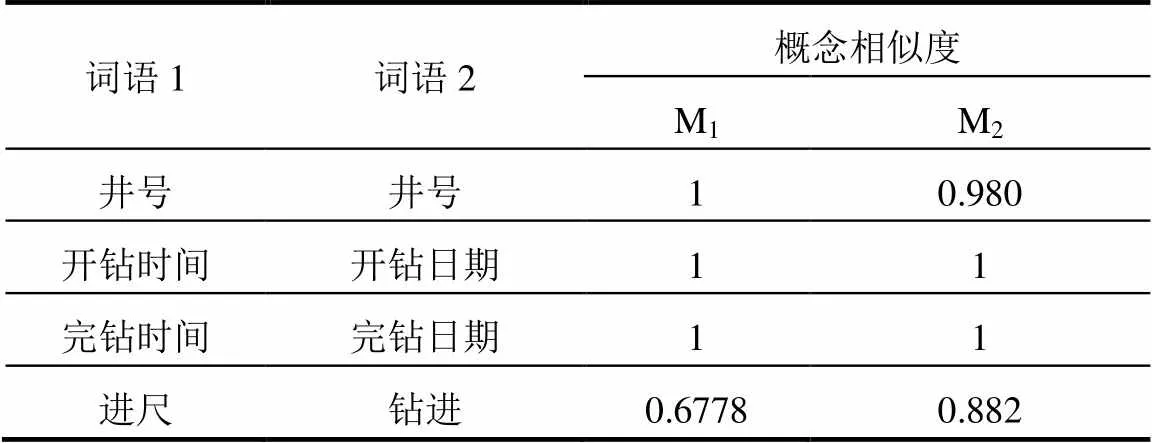
表1 钻井作业本体实验结果
表1为方法1和方法2计算得到的概念相似度, 其中, M1、M2分别为方法1和方法2计算所得的相似度值. 结果表明, 基于树结构的本体概念相似度计算模型能够方便地用来计算领域本体概念间的相似度, 并能较好地反应本体映射关系, 在满足映射质量的前提下, 极大地简化了计算过程. 如对于“进尺&钻进”匹配对, 在钻井领域, 二者所表达的内容是相同的, 因此, 主观判断其相似度应该更高, 本文所用方法的计算结果更符合人们的直观判断.
3 结语
本文以本体树结构为基础, 提出了一种合理的概念相似度计算方法, 该方法依赖于重构本体树进行本体映射过程, 确定了将XML DTD模式的节点基于节点间关系转换为树结构的方法, 并着重于寻找对象之间的等价性, 通过比较属性, 建立对象之间的匹配, 这比在信息共享中寻找属性之间的匹配更为有效, 并简化了计算过程, 有效确保了计算的全面性、准确性. 不足之处在于凭经验设定的各个权值对结果造成了一定的误差. 在以后的工作中, 需要进一步完善概念语义相似度的计算方法, 比如本体树中如何更好的确定边权值等.
1 甘健侯,姜跃,夏幼明.本体方法及其应用.北京:科学出版社,2011.
2 程勇,黄河,邱莉,等.一个基于相似度计算的动态多维概念映射算法.小型微型计算机系统,2006,27(6):975–979.
3 黄果,周竹荣,周亭.基于领域本体的语义相似度计算研究. 计算机工程与科学,2007,29(5):112–117.
4 范弘屹,张仰森.一种基于HowNet的词语语义相似度计算方法.北京信息科技大学学报,2014,29(4):42–45.
5 刘紫玉,黄磊.基于领域本体模型的概念语义相似度计算研究.铁道学报,2011,33(1):52–57.
6 姜华.改进的本体语义相似度计算方法.计算机工程与应用, 2008,44(36):143–145.
7 刘宏哲,须德.基于本体的语义相似度和相关度计算研究综述.计算机科学,2012,39(2):8–13.
8 鲁德浩,郏东耀.一种改进的概念相似度计算方法.郑州大学学报(理学版),2010,42(1):9–12.
9 Ehrig M, Sure Y. Ontology mapping-an integrated approach. Lecture Notes in Computer Science, 2004, 3053: 76–91.
10 严丽,马宗民,刘健,于戈.模糊XML DTD到UML数据模型的转换.小型微型计算机系统,2009,30(4):586–592.
11 Chiabrando E, Likavec S, Lombardi I, et al. Semantic similarity in heterogeneous ontologies. Ht’11, Proc. of the, ACM Conference on Hypertext and Hypermedia, Eindhoven. the Netherlands. June, 2011. 153–160.
12 游彬,严岳松,孙英阁,等.基于HowNet 的信息量计算语义相似度算法.计算机系统应用,2013,22(1):129–133.
13 许云,樊孝忠,张锋.基于HowNet 的语义相关度计算.北京理工大学学报,2005,20(5):411–414.
14 Wen, Yu, Gao, et al. Research on concept semantic similarity computation based on ontology. IEEE, International Conference on Computing, Control and Industrial Engineering. IEEE. 2011. 284–287.
15 刘群,李素建.基于《HowNet》的词语语义相似度计算.计算语言学及中文信息处理,2007,(7):59–76.
16 董振东,董强.HowNet knowledge database.http://www. Keenage.com/. [2014-05-05].
Ontology Concept Similarity Calculation Based on Tree Structure
XU Ying-Zhuo, JIA Huan
(Institute of Computer, Xi’an Shiyou University, Xi’an 710065, China)
With the wide application of ontology in data integration, the concept of ontology-oriented similarity calculation became a hot issue of concern. In view of the problems that current domain ontology concept similarity calculation processes are complex, this paper proposes a concept of ontology similarity calculation method based on tree structure. The thought of this method is that through adding virtual nodes and restructuring, refactoring ontology tree, and then comparing and mapping object properties, at last, the computation of the concept of ontology semantic similarity results are obtained. The experimental results show that the method is effective to use the concept of ontology semantic information, reasonable calculation results are obtained, it can also simplify the calculation process.
ontology; concept similarity; tree structure
国家自然科学基金(51574194);陕西省科技工业攻关项目(2014K05-02,2016GY-144);陕西省教育厅专项科研计划项目(15JK1567)
2016-06-29;
2016-08-08
[10.15888/j.cnki.csa.005667]
