一种变异真值表故障模型的神经网络测试生成算法

戴金玲，许爱强

（1.海军航空工程学院 研究生二队，山东 烟台 264001；2.海军航空工程学院 科研部，山东 烟台 264001）

一种变异真值表故障模型的神经网络测试生成算法

戴金玲1，许爱强2

（1.海军航空工程学院 研究生二队，山东 烟台 264001；2.海军航空工程学院 科研部，山东 烟台 264001）

针对传统测试生成算法计算复杂度高的问题，提出一种针对逻辑门功能异常的故障模型，并给出了基于遗传优化的神经网络测试生成算法。首先，与传统算法以固定值故障为目标不同，构建更全面的变异真值表故障模型，在考虑各输入条件下故障的不同权重的同时，按故障模型自动生成故障字典；然后，测试生成算法利用逻辑门的二值神经网络能量函数，构成数字电路的约束网络；最终，调用故障字典向约束网络注入故障，通过遗传算法求解出被测电路的测试集。仿真实验结果显示，所提的故障模型更加全面，且测试生成算法具有正确性和有效性。

变异真值表故障模型；神经网络；遗传算法；测试生成

Abstract:In order to solve the problem of the high complexity of the conditional test generation methods，a new fault model based on functional fails and neural network test generation algorithmare proposed.At first，different from conditional methods based on stuck-at fault model， a mutated truth table fault model is built considering the weights of faults under different inputs.The fault dictionary is automatically formed by fault model.Secondly，the constraint network is constructed with energy function of two-valued neural network.Lastly，faults are injected into the constraint network referring to the fault model，and the testing sets are get by genetic Algorithm.The experimental results show that the fault model and the test generation method are effective.

Key words:mutated truth table fault model； neural networks； genetic algorithm； test generation

传统的组合电路测试生成算法是一种确定性的生成方法，即分析被测电路（Circuit under test，CUT）的门级描述，以推导出目标故障的测试向量，或证明其是不可测的，主要有D算法，PODEM（Path-orientated decision making，PODEM）算法[1]，FAN（Fujiwara and Shimono）算法[2]等。随着数字集成电路越来越复杂，传统的测试生成方法因其高计算复杂度已经不再适用，建立真实的故障模型、研究新型有效的测试生成算法具有十分重要的理论价值和实际意义。近年来，神经网络在许多领域的应用[3-7]都取得了成功，许多学者提出利用神经网络模型和遗传算法来解决测试生成问题。文献[8]将组合电路的多故障测试生成问题转化为单故障测试生成问题，通过建立被测电路的二值神经网络约束网络和遗传算法，求解能量函数的最小值点，有效地得到多故障电路的测试矢量；文献[9]成功将三值神经网络和遗传算法结合起来应用到数字电路的多故障测试生成中，与二值神经网络算法相比，明显减少了测试时间；文献[10]针对遗传算法存在的搜索空间大、时间长的不足，提出一种电路分块方法，优化了遗传算法在测试生成中的应用。已有神经网络的应用，都是建立在固定值故障模型（Stuck-At Fault model， SAF）基础之上的。然而，有文献[11]指出，仅用固定值故障模型代表数字电路中的所有故障是不充分的。因此有必要建立更真实有效的故障模型，并通过神经网络和遗传算法进行测试生成。

文中提出的组合电路测试生成系统首先基于CUT所有基本逻辑门类型的真值表，针对各输入构建故障字典；然后，通过逻辑门的二值神经网络能量函数表示被测电路，并自动调用故障字典存储的故障信息向被测电路中注入故障，通过遗传算法，求得最终的测试集。

1 变异真值表故障模型

故障模型主要研究逻辑门功能异常对其真值表的影响，因此需要对逻辑门功能失效时真值表的变化进行分析。对于任意的逻辑门类型G，正常状态时的真值表为TG，保持真值表中输入列部分不变，当G的内部电路中有故障时，若其对应的真值表T*G≠TG，则称T*G为逻辑门类型G的一个变异真值表（Mutated Truth Table，MTT）。MTT与真值表的区别仅在于输出列中的常见逻辑值不同。

显然，G中包含不止一种内部故障，考虑能使电路发生功能异常的硬故障：开路与短路，通过仿真或实验手段可得多个与这些故障相对应的MTT，最终这些MTT的集合即为逻辑门类型G的故障字典。显然，G中包含不止一种的内部故障，因此通常存在多个与这些内部故障相对应的MTT，它们即构成了该逻辑门类型 G 的故障字典， 记为 DG={＜T*G，k，λG，k＞|k=1，2，…，NG}，其中 NG表示 MTT 的数量；λG，k表示对应的MTT等于T*G，k的累计故障计数。显然，一个MTT对应的内部故障数量越多，它在逻辑门的故障行为空间中出现的概率就越大。考虑到在实际数字电路中，不定态‘X’是不存在的，既可能为‘1’也可能为‘0’，或者在这两个逻辑值之间随机跳变，因此需要对故障字典进行整理，将‘X’状态按某种概率分配到‘0’和‘1’上，最终建立可被测试生成算法调用的故障字典。

测试覆盖率定义为测试集检测出的故障之和比上所有逻辑门上注入的故障之和，其计算公式为

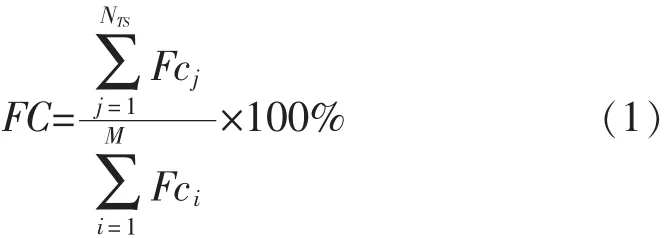
其中NTS为CUT生成的测试集向量数，M为CUT的逻辑门数，Fcj为第j个测试向量所检测到的故障数量，Fci为第i个逻辑门中注入的故障数量。

2 测试生成算法

2.1 组合电路的神经网络模型

二值神经网络的能量函数[12]为：

式中:N是神经网络中神经元的数目；Ii是神经元i的阈值；Tij是神经元i和j之间的权值；Vi是神经元i的状态值；K是常量。

用Hopfield模型中的能量函数来表示基本门电路的传输特性：对符合一种基本门电路功能函数的取值称为这种门电路的一个相容状态，其他不符合功能函数的取值称为门的非相容状态。当基本逻辑门的输入输出值符正确的逻辑关系时，对一种门电路的一个相容状态，能量函数E=0，否则不为零。基于此能量函数，则将测试生成问题转化为数学问题，通过式（1）得出基本门电路的而二值神经网络能量函数如表4所示，其中第一列为逻辑门的类型，第二列为输入，第三列为输出，第四列为逻辑门的神经网络能量函数。

表1 基本逻辑门的能量函数

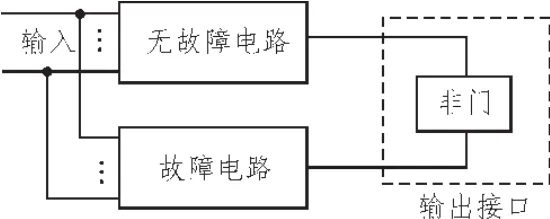
图1 单输出电路的约束网络

数字电路中一个逻辑单元有故障，如果存在电路的一组输入使电路的输出在无故障与有故障时相异，则这组输入就为该故障的一个测试向量。实现神经网络故障测试，需要构建CUT的约束神经网络能量函数。约束网络由故障电路（已注入故障）、无故障电路和一个接口电路组成。图1所示为单输出电路，接口由一个非门组成；图2所示为多输出电路，接口由数量为输出端口数的二输入异或门和一个或门构成，并且或门的输出为‘1’，这样的限制是为了使约束网络的输入矢量为故障的测试矢量时，CUT的故障输出与无故障输出不同。约束网络的能量函数与逻辑门构造方法相同。

对于任何一个组合逻辑电路，利用推导出的基本逻辑门电路的二值神经网络能量函数，就能获得相对应的组合逻辑电路的二值神经网络能量函数。将每一种基本门电路定义为结构类型，根据基准电路给出的各基本门电路的输入输出关系，把它们组合起来就构成了被测电路的神经网络模型。

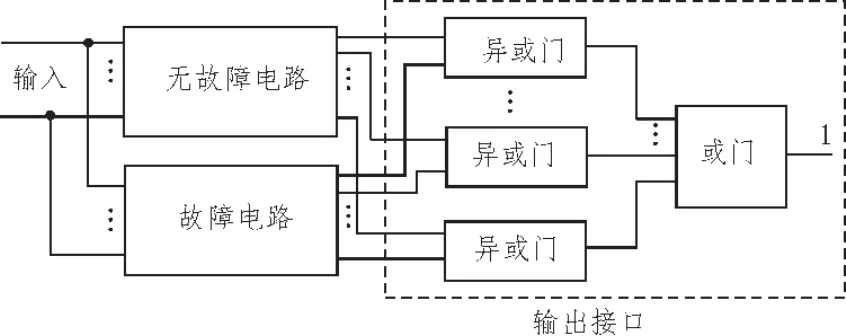
图2 多输出电路的约束网络

2.2 遗传算法

根据电路的约束电路可得，电路中一个故障存在测试矢量的充要条件是：在故障点处取与正常电路相反的值时，约束网络处于相容状态，即对应神经网络的能量函数值为0。因此，通过对故障字典中的故障计数来决定故障注入的排序，对其测试生成，而数字电路故障的测试生成问题就可以表示为求能量函数的最小值点问题，实质上是将测试生成问题数学化。

遗传算法模仿了生物进化论，利用了选择、复制、交叉和变异等策略，能够提供全局并行搜索和鲁棒性搜索，并且对连接权值不敏感[13]，因此本文通过遗传优化算法求能量函数的最小值以得到故障的测试矢量。设置种群的规模为N，当前种群中的个体为xi（i=1，2，…，N），个体的编码和适值函数的定义为：

其中 E（x）为约束网络能量函数，f（x）的取值在0到1之间，个体 xi的适值 f（x）越大，说明 xi的性能越好，使f（x）的值为1的个体xi就是使能量函数等于零的个体，即为给定故障的一个测试矢量。

二值神经网络遗传算法流程图如图3所示：1）设置初始种群规模，并随机产生初始种群；2）适应度值计算：计算适应度值最大和最小的值；3）选择策略：根据赌盘选择选出两个个体；4）交叉、变异：设置交叉概率和变异概率，对选出的两个个体进行交叉和变异。

图3 二值神经网络遗传算法流程图

3 仿真实验与结果分析

以CMOS （complimentary metal-oxide-semiconductor）工艺的两输入与非门为例[14]（见图 4），假设其输入依次为“00”、“01”、“10”、“11”，真值表输出相应为[1，1，1，0]T，则对其进行故障注入和分析可得如表 2 所示的故障字典。 其中，TN1、TN2、TP1、TP2分别为逻辑门中的MOS管 （N型或P型），d、g、s分别表示MOS管的漏极、栅极和源极，符号O（open）、S（short）分别表示元器件上的局部开路和短路，全局的节点桥接则表示为（n1，n2）_S（其中n1和n2表示不属于同一元器件的两个节点）。合计行中给出了注入故障的总数（此处为27）和不同输入组合分别覆盖的故障数量（此处为[9，18，18，12]T）。

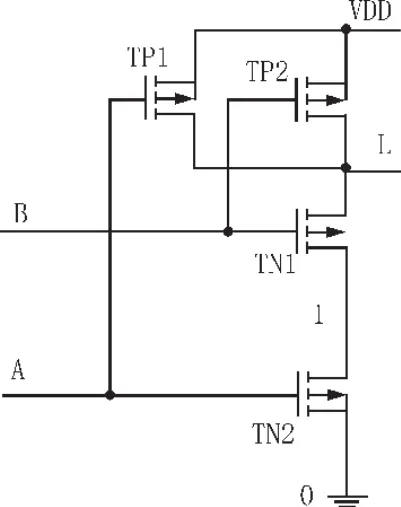
图4 两输入与非门电路图

表3所示为将不定态‘X’按等概率进行分配得到的结果，其中第2、3列分别为MTT列表和整理后其对应的故障计数，以表 2中[1，X，1，0]T为例，引起该MTT的故障数为4，将‘X’等概率分配后，各以2的权重加到[1，1，1，0]T和[1，0，1，0]T上，而[1，1，1，0]T为该逻辑门的正常输出，因此不计入MTT中，而将[1，0，1，0]T的故障计数加 2，以此类推，得到改进的两输入与非门故障字典，如表3所示。

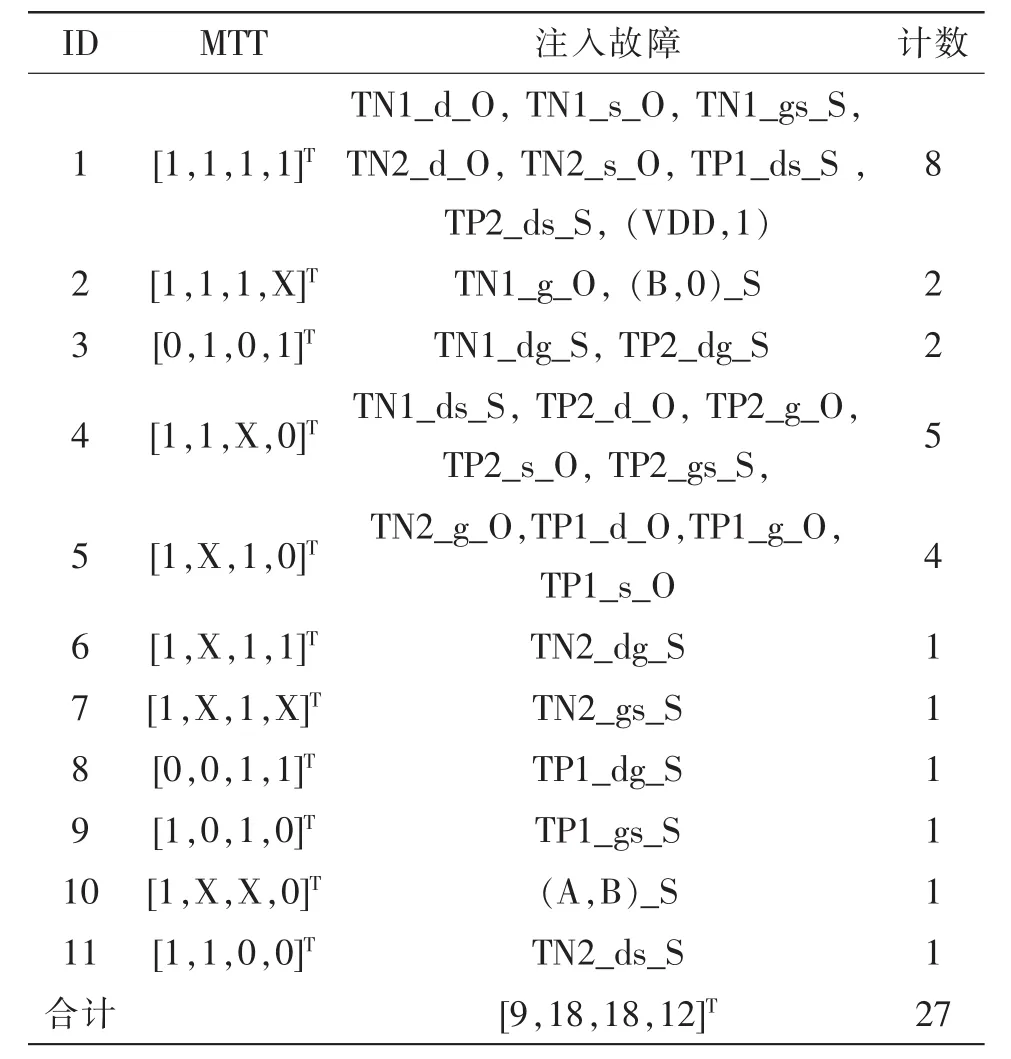
表2 两输入与非门故障字典

表3 改进的两输入与非门故障字典

表4 改进的逻辑门故障字典

由表3可见：1）向逻辑门电路中注入硬故障均会引起功能异常，而功能异常的具体形式与故障发生的位置有关；2）固定1故障出现的次数最多，高于其他任何一种故障类型，可见，固定值故障的确是一种重要的故障模式；另一方面，非固定值故障的比重之和高达70.4%，由此可见，经典的固定值故障模型并不能代表数字电路中的真实故障情况。

根据改进的故障字典的内容，最终可建立如表4所示的用于测试生成过程调用的故障字典，内容为逻辑门的所有输入组合下的故障计数，其中单输入逻辑门（如 Inv）依次有‘0’、‘1’两种输入，两输入逻辑门依次考虑“00”、“01”、“10”和“11”4 种输入组合。测试生成调用字典的过程是将故障数权重较大的输入作为优先注入的对象，并尽可能覆盖逻辑门的所有输入组合。按照本文测试生成算法的描述，对国际基准电路进行了测试生成 （仿真实验在3 GHz CPU、4 GB RAM的计算机上执行），并验证了测试覆盖率，设置种群大小为25，迭代次数为50，变异概率0.01，交叉概率为0.25。实验结果如表5所示，其中第1列为被测电路名称，第2、4列分别为本文与参考文献[7]中的测试生成时间，第3、5列分别为本文与参考文献[7]中生成测试集的故障覆盖率。

由表5可见：1）文中提出的算法有较高的效率与故障覆盖率；2）传统的固定值故障模型下，文献[7]得到的故障覆盖率均为100%，其结果过于乐观；而变异真值表故障模型更能体现真实的故障覆盖情况。

4 结 论

本文首先从电路的内部故障出发，根据逻辑门不同的外部功能异常表现，构建了更全面的变异真值表故障模型，并考虑了各输入条件下故障的不同权重，按故障模型自动生成故障字典。基于逻辑门的二值神经网络能量函数所构成的约束网络，调用故障字典向约束网络注入故障，通过遗传算法求解出被测电路的测试集。仿真实验结果显示，本文建立的故障模型更加全面和真实，测试生成算法具有较高的故障覆盖率和较短的测试时间。

[1]KAI Y,KWANG T C,LI C W.TranGen:A SAT_Based ATPG for Path-Oriented Transition Faults[C]//Proceedings of Asia and south pacific design automation conference，2004:92-97.

[2]杨士元.数字系统的故障诊断与可靠性 [M].北京：清华大学出版社，2000.

[3]潘中良，陈翎.基于神经网络的电路多故障测试及并行实现 [J].仪器仪表学报，2002，23 （6）:680-681.

[4]韩之刚，高兰芝，宫海燕，等.基于三值神经网络数字电路多故障测试生成算法 [J].煤矿机械，2008，29（1）:205-208.

[5]徐红兵，李焱骏，王厚军.一种基于混沌神经网络的自动测试生成算法[J].仪器仪表学报，2002，23（5）:77-79.

[6]薛维琴，李莉华，戴明.基于FPGA的人工神经网络系统的实现方法[J].电子设计工程，2010，18（9）:151-154.

[7]张宇翔，黄力宇.Hopfield网络求解TSP两种改进算法的仿真研究[J].电子设计工程，2009，17（10）:119-121.

[8]杨兴，谢志远，冯力娜.神经网络在组合电路多故障测试生成算法中的应用 [J].电力科学与工程，2009，25（3）:37-41.

[9]吴丽华，王旭东，史芳芳，等.遗传优化三值神经网络多故障测试生成算法 [J].仪器仪表学报，2010，31（8）:1744-1749.

[10]许杰，涂小辉.基于改进遗传算法的组合电路测试生成[J].实验室研究与探索， 2012，31（7）:76-78.

[11]TANG X F， XU A Q， LI W H， et al.Fault Models of CMOS Gates:An empirical study based on mutation analysis[C]//Proceedings of IEEE International Conference on Software Engineering and Service Sciences.Beijing:IEEE，2014:916-920.

[12]赵莹，吴丽华，王轸.基于神经网络的数字电路多故障测试生成算法 [J].电机控制与学报，2006，10（5）:478-481.

[13]李鸣，彭大海，高娜，等.基于混沌和遗传算法的优化测试生成算法 [J].微计算机信息，2005，21（8）:125-127.

[14]康华光，皱寿彬，秦臻，等.电子技术基础[M].北京:高等教育出版社，2006.

Testing generation algorithm based on neural networks for mutated truth table fault model

DAI Jin-ling1，XU Ai-qiang2
（1.Graduate Student Team Two， Naval Aeronautical and Astronautical University，Yantai264001，China； 2.Department of Scientific Research，Naval Aeronautical and Astronautical University，Yantai264001，China）

TP407；TP301.6

A

1674－6236（2017）19-0174-05

2016-08-24稿件编号201608175

戴金玲（1991—），女，江苏溧阳人，硕士研究生。研究方向：电子信息系统测试与诊断技术。