基于改进型的交叉耦合双电机同步控制方法

2017-10-12陆梦羽张旭秀吴春梅

大连民族大学学报 2017年5期

关键词：同步控制论域补偿器

陆梦羽，张旭秀，刘影，吴春梅

(大连交通大学电气信息学院，辽宁大连 116028)

基于改进型的交叉耦合双电机同步控制方法

陆梦羽，张旭秀，刘影，吴春梅

(大连交通大学电气信息学院，辽宁大连 116028)

针对传统双电机同步控制精度低，难以实现同步控制的不足，以PMSM为被控对象，建立其数学模型，在传统交叉耦合控制的基础上提出基于模糊PID控制的交叉耦合控制策略。采用遗传算法对参数进行优化，确定改进模糊控制器的参数范围，实现参数自整定。仿真结果表明改进后的交叉耦合控制方法对双电机控制的同步性和抗干扰性都有所提高。

交叉耦合控制；模糊控制；双电机

Abstract:It is difficult to realize the synchronous control for the traditional double motor because of the low precision. Taking the permanent magnet synchronous motor (PMSM) as the controlled object, we set up its mathematical model, and propose the cross coupling control strategy based on fuzzy PID control on the basis of the traditional cross coupling control. The genetic algorithm is used to optimize the parameters, determine the parameter range of improved fuzzy controller, and realize the self-tuning of parameters. The simulation results show that the synchronization performance and anti-jamming performance of the improved cross coupling control strategy of double motor control are both improved.

Keywords:cross-coupling control; fuzzy control; double motor

如今工业技术与科技快速发展，电机已经成为不可缺少的器件，对电机系统的控制性能也提出了更高的要求。目前，传统的单电机驱动方案已经无法满足生产要求，很多领域都需要多台电机协同工作。多台电机之间在速度、位置等方面存在一定的约束关系，需要采取一定的控制策略，实现多台电机之间同步控制，满足高效率生产的要求。多台电机的同步控制问题受到国内外学者的广泛关注[1-3]。

为了提高双电机的同步精度和抗性性能，1980年Koren提出了交叉耦合方案，有效解决了双电机同步问题。文献[4-5]在补偿回路采用固定增益，对电机的跟踪采用传统PID控制，双电机间的转速误差响应和系统动态响应情况都没有达到理想标准，且同步性较差；文献[6-7]加入模糊PID控制，没有利用遗传算法对参数进行自整定，使得电机动态响应效果和跟踪效果不够理想。

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)是一个高耦合、非线性的数学模型，本文在双电机同步控制上采用交叉耦合的方式，在补偿增益上采用改进的模糊控制替代传统的固定增益控制。通过Matlab/Simulink实验平台搭建模型并进行仿真，实验证实改进后的方法其同步性和抗干扰性都有所提高。

1 永磁同步电机模型

为了便于分析，对永磁同步电机建立模型时做如下处理：假设磁饱和效应及铁心涡流、磁滞损耗为零；相绕组中感应反电势呈现正弦波状；电机电流为对称三相正弦波电流；永磁体没有阻尼作用；永磁材料的电导率为零；忽略温度、磁场变化对电机参数的影响。在定子电流给定的情况下，采取id=0的矢量控制。PMSM在d-q坐标下的数学模型为[8]

(1)

式中，ud、uq为定子电压在d、q轴上各自的分量；id、iq为定子电流在d、q轴上各自的分量；Ld、Lq为d、q轴的定子电感分量；ψd、ψq为d、q轴的定子磁链分量；R为定子电阻；ψf为转子上永磁体产生的磁链；P为极对数；TL为负载；B为转矩阻尼系数，与转速成正比。

2 基于改进的模糊控制速度补偿器设计

传统的交叉耦合控制如图1，K1、K2为耦合系数，K1、K2越高系统越不稳定，基于此提出一种基于模糊PID的交叉耦合控制方法。该方法采用PID补偿器来解决两电机受到干扰而速度发生变化的问题，同时将操作经验转化为模糊规则的优点，对两台电机实施控制作用。模糊控制器的两个输入分别为两电机之间的转速差和偏差变化率，同时用遗传算法对参数进行自整定，确定参数范围。

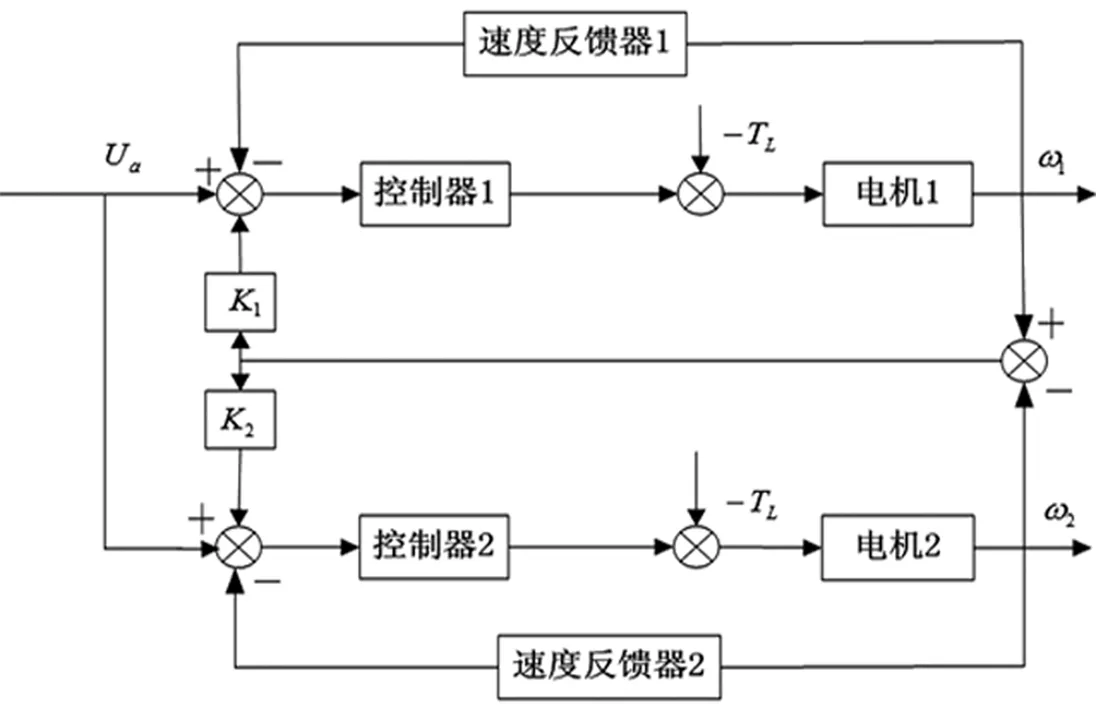
图1 交叉耦合控制流程图

2.1 基于模糊PID的交叉耦合多电机同步控制原理

模糊规则的建立是以人们的操作经验为基础，跟踪补偿两台电机的速度，再通过仿真对比得到相对最优算法。控制原理如图2。

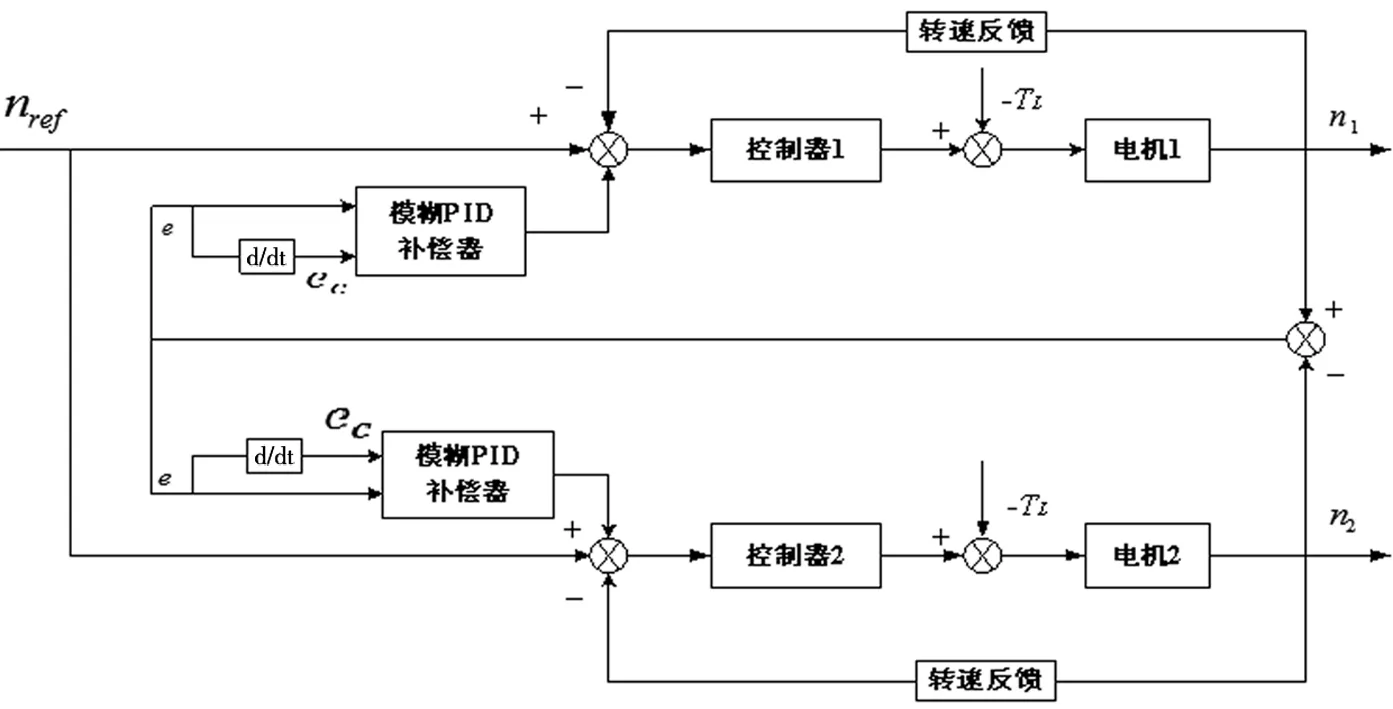
图2 模糊PID交差耦合多电机同步控制原理图

2.2 基于遗传算法的参数整定

本文中两电机速度补偿器的参数范围是通过遗传算法的优化，得到模糊PID补偿器参数范围。遗传算法参数整定流程如图3。

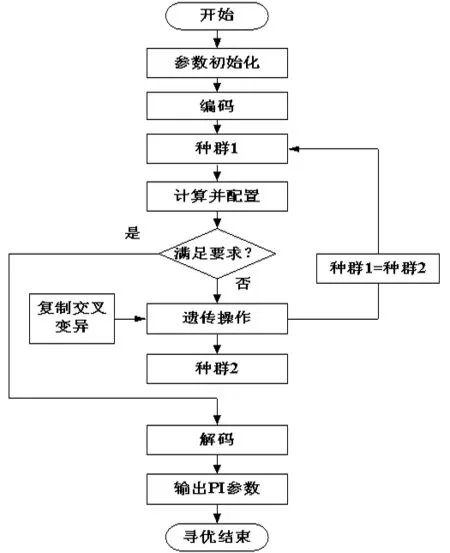
图3 遗传算法参数整定流程图

2.3 模糊PID补偿器的实现

(1)确定模糊PID补偿控制器的输入、输出及其基本论域。偏差e和偏差变化率ec作为输入，其中e的基本论域为[-3,3]，ec的基本论域为[-120,120]，即模糊控制器的位数为二维。同时确定Δkp、Δki的范围，kp、ki的取值范围根据遗传算法求得分别为[1,3]、[0,10]，Δkp、Δki的基本论域分别为[-5,5]、[-2,2]，模糊PID补偿器的初始值为kp=2，ki=5。

(2)输入变量模糊化:

a．确定输入变量e、ec和Δkp、Δki基本论域在模糊集上的论域：

E={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；

EC={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；ΔKP={-5,-4,-3,-2,-1,0,1,2,3,4,5}；

ΔKI={-2,-1,0,1,2}；

设模糊子集为：

E={NB,NM,NS,Z,PS,PM,PB}；

EC={NB,NM,NS,Z,PS,PM,PB}；

ΔKP={NB,NS,Z,PS,PB}；

ΔKI={NB,NS,Z,PS,PB}。

b. 确定变量隶属函数。文章采用三角形分布的隶属函数Trimf。ΔKP、ΔKI隶属度函数曲线也取为三角形分布。

(3)建立PID参数模糊控制规则表。本文的控制对象为两台转速同步的PMSM，根据专家知识和不断地试验，ΔKP、ΔKI的控制规则见表1、表2。

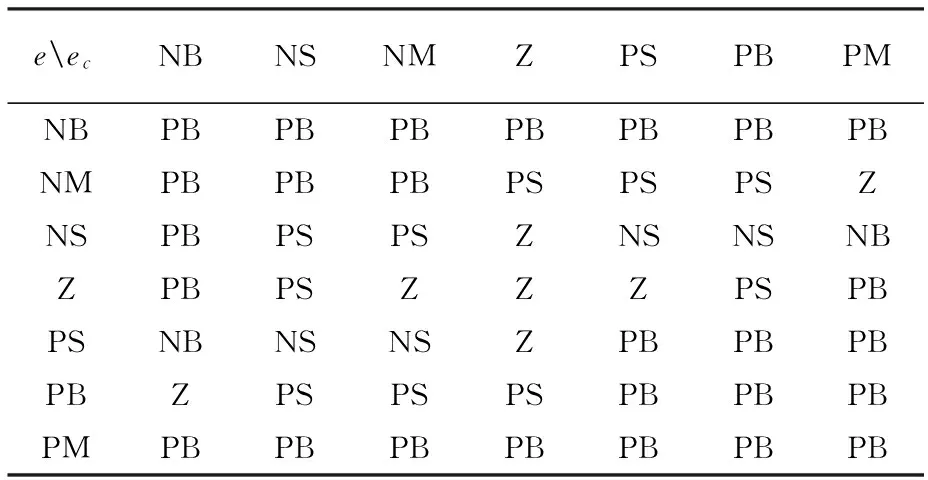
表1 ΔKP模糊控制表

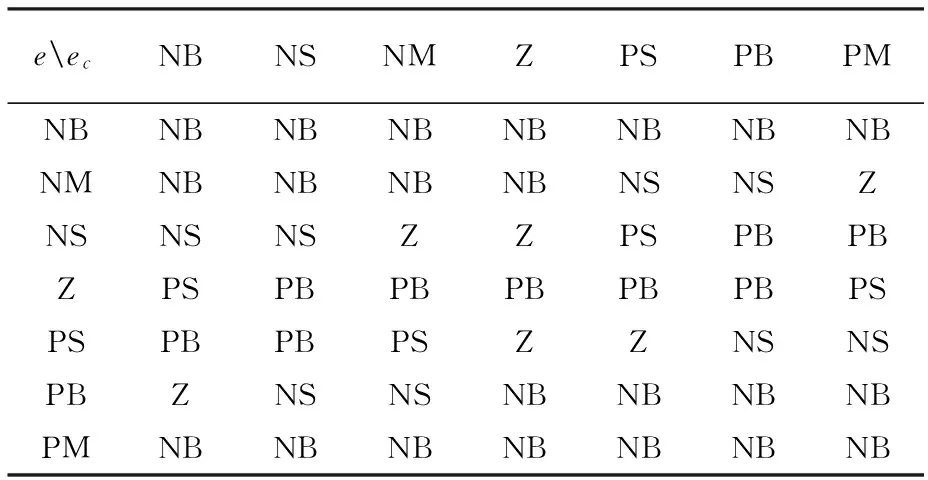
表2 ΔKI的模糊控制表

(4) 模糊推理及判决。由ΔKP的模糊规则表可得出以下的控制规则：

IfEisNBandEcisNBthenΔKPisPB；

⋮

IfEisNBandEcisPBthenΔKPisPB。

(5) 模糊PID控制算法。前文已经确定了E、Ec、ΔKP、ΔKI模糊子集的隶属度函数，模糊PID算法的核心是进行模糊推理，实现参数的自整定，通常将模糊规则表保存在程序存储器中供查询。参数KP、KI调整过程如下：

(2)

在两台电机实际运行过程中，通过计算机测控系统实时监测两台电机的实际转速值，并计算出它们之间的转速偏差，随之得出偏差变化率，通过模糊化得到E和EC，再查询模糊调整矩阵即可得到KP、KI参数的调整量，从而实现对控制器的整定。

3 系统仿真

在Simulink仿真环境下，根据前面所设计的基于模糊PID补偿器的交叉耦合多电机同步控制系统，采用两台PMSM搭建同步控制系统仿真，如图4。交流永磁同步电机参数如下：额定转速500 r·min-1，定子电阻2.875 8 Ω，交轴、直轴分别为Lq=Ld=8.5 mH,转动惯量J=0.008 5 kg·cm2，极对数P=4,额定转矩Te=5 N·m,转子磁通φf=0.175 Wb。

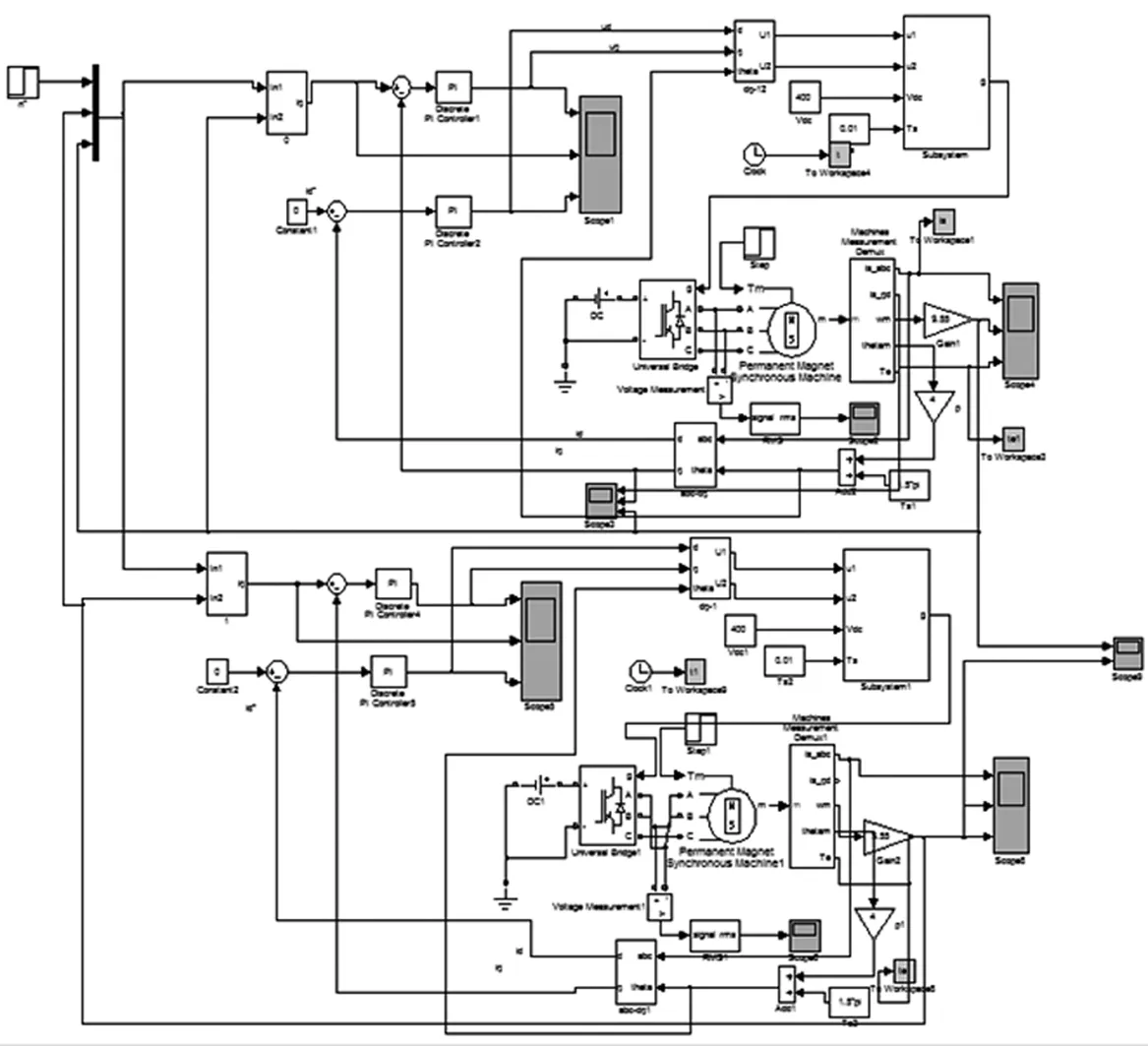
图4 基于模糊PID的交叉耦合多电机同步控制原理

把5 N·m的阶跃信号作为启动时的给定信号，两台电机启动时转速如图5(a)，从图中可以看出在t=0.01 s时，两台电机已经实现转速同步，在t=0.07 s时加10 N·m的扰动，仿真结果如图5(b)。

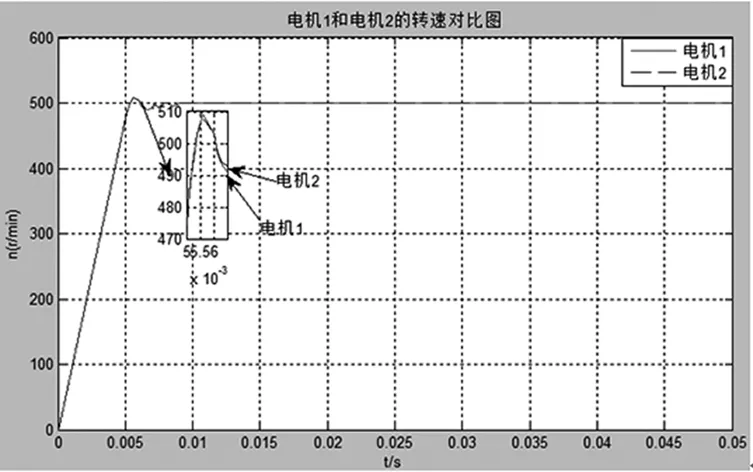
(a)带载启动

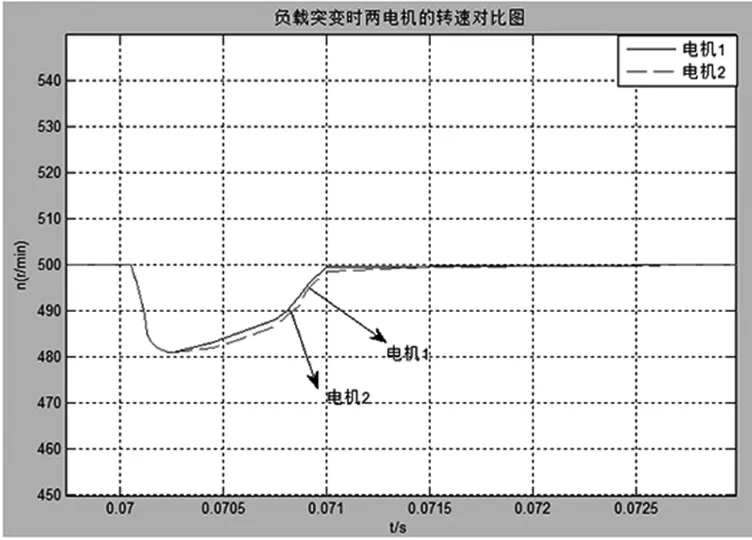
(b)负载突变

用比较两个控制系统的方式就会得到相对最优的方法，进行择优，提高控制效率，根据上面的分析结果得出两种控制方法的性能指标如下：传统交叉耦合控制下得到两台电机之间的同步误差Δnerror=0.32%，突加负载扰动后,电动机动态速降Δnmax=3.6%；模糊PID控制的交叉耦合同步控制下得到两台电机之间的同步误差Δnerror=0.12%，突加负载扰动后,电动机动态速降Δnmax=1.8%，是传统的动态速降的一半。这样会容易得到后者的同步性能以及抗扰动能力相对于前者的控制方法更优，可用于精度要求较高的场合。

在搭建的实验平台上进行测试，与传统PID补偿器速度跟踪情况进行比较，使两台电机在空载情况下对电机1突加20 N·m负载扰动，使用传统PID补偿器时两台电机速度响应曲线如图6，使用模糊PID补偿器时两台电机速度响应曲线如图7。

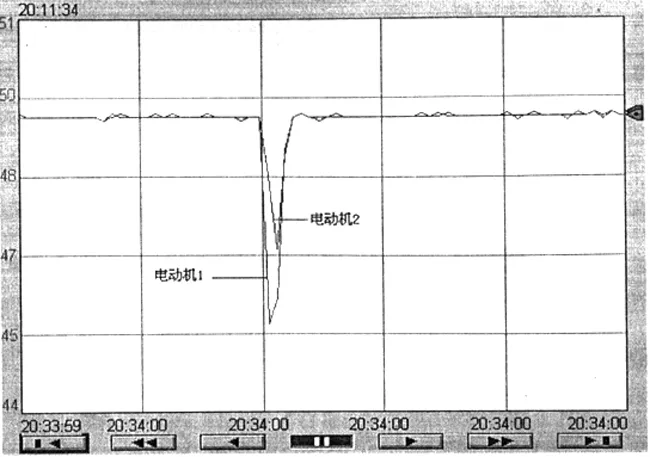
图6 传统PID补偿器时速度跟随曲线

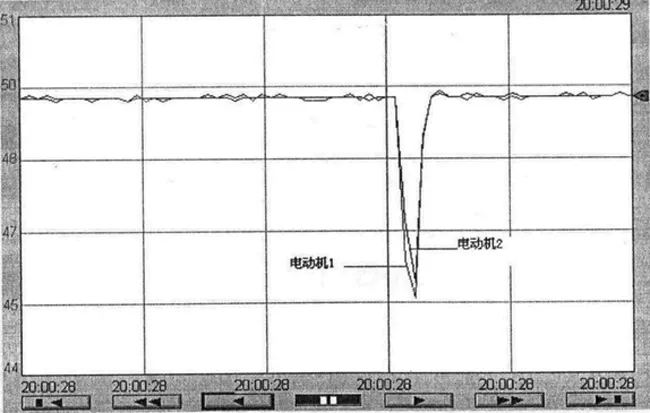
图7 模糊PID补偿器时速度跟随曲线

经对比模糊PID补偿器的交叉耦合同步控制方式有较好的同步精度，增强系统抗干扰性与对未知因素的适应性。

4 结语

本文首先分析永磁同步电机的数学模型，在传统的交叉耦合基础上提出基于模糊PID补偿器的交叉耦合同步控制方式，采用PID补偿器来解决两电机受到干扰而速度发生变化的问题，同时将专家操作经验转化为模糊规则的优点，对两台电机实施控制作用，并用遗传算法进行参数自整定确定参数范围，仿真结果表明基于模糊PID的交叉耦合控制方式具有更好的同步性和抗干扰性。

[1] 高德超. 多电机系统协同控制研究[D].济南：济南大学,2015:16-18.

[2] 范志龙.基于永磁同步电机的多电机同步控制系统的研究[D].长沙：湖南大学,2012:20-24.

[3] 姚武军.多电机同步控制策略研究[D].湘潭：湘潭大学,2013:35-39.

[4] 姜晓平,朱奕,伞冶.大功率随动试验台多永磁同步电机同步控制[J].电机与控制学报,电机与控制学报,2014(4):88-95.

[5] 胥小勇,孙宇,蒋清海.改进型相邻耦合结构的多电机比例同步控制[J].仪器仪表学报,2012(6):1254-1260.

[6] 王国亮.基于模糊PID补偿器的多电机同步控制策略研究[D].沈阳：东北大学,2006:56-61.

[7] 孙怡.基于模糊PID控制的多电机同步控制系统的研究[D].上海：华东理工大学,2012:57-63.

[8] 杨会玲. 永磁同步电机调速系统控制算法的研究[D].天津：天津大学,2009:45-47.

(责任编辑赵环宇)

SynchronousControlMethodofDoubleMotorbasedonImprovedCross-coupling

LUMeng-yu,ZHANGXu-xiu,LIUYing,WUChun-mei

(School of Electrical Information, Dalian Jiaotong University, Dalian Liaoning 116028, China)