基于粒子群的LMS算法在信号滤波降噪中的应用

赵轶骁, 汪镭(同济大学 电子与信息工程学院, 上海 201804)

基于粒子群的LMS算法在信号滤波降噪中的应用

赵轶骁, 汪镭
(同济大学 电子与信息工程学院, 上海 201804)

在自适应滤波算法中，LMS算法是最常用的算法之一，因为具备结构简单，易于实现，性能稳定，计算复杂度低等特点。然而，LMS算法也存在缺点，比如，收敛速度较慢，收敛精度低的问题，这就影响LMS算法在收敛性要求较高的领域中的应用。使用粒子群算法对LMS算法进行改进，可以将LMS滤波设计变成对LMS滤波参数优化的问题， 利用粒子群算法的优化能力，使得滤波参数得到全局最优解。以此可以提高LMS滤波算法的收敛性能，从而提高滤波性能。

自适应滤波; LMS算法; 粒子群算法

Abstract： In the adaptive filter algorithms, LMS algorithm is one of the most common algorithms because of its simple structure, facile realization and stability, low computational complexity. But， LMS algorithm has also some defects, for example, low rate of convergence and convergence precision. Those problems have impacted on the application in high convergence fields. PSO algorithm can be used to improve the LMS algorithm. The designation of the LMS filter can be transferred to optimization problem for the parameters of LMS filter. The optimization of PSO algorithm is utilized to get the global optimal solution of filter parameters. In this way, convergence of LMS algorithm can be improved, and the performance of filter also can be improved.

Keywords： Adaptive filter; LMS algorithm; PSO algorithm

0 引言

自适应滤波算法在目前数字信号处理应用中，是非常重要的组成部分。其中，基于最小均方差理论发展起来的LMS算法(Least mean square)是目前自适应滤波中应用最广泛的一种。它使用梯度下降的原理，让均方差达到最小。在LMS算法中，算法的收敛速度和收敛精度是自相冲突的指标，两者通过调整收敛因子μ达到平衡。所以，如何更好的提高LMS算法的收敛性能一直是被研究的问题。，诸如，变长LMS算法，变阶数LMS等等，这些改进一步步完善了LMS算法，但是只在特别的情况下有效果，通用能力弱。

粒子群算法是基于群体智能的搜索优化算法，通过在搜索空间内的对多点搜索，通过搜索到当前最优值来找到空间内的全局最优点。这种算法以其实现容易、精度高、收敛快等优点。文献[1]中将PSO运用到LMS中去，在多重模态的问题上，解决了收敛速度和收敛精度的冲突的问题。本文正是利用该算法的诸多优点，对LMS算法进行改进，弥补算法收敛性存在的不足能力，提高它的滤波性能，并将它用于信号降噪中去。

信号降噪是一直被广泛使用的技术，在尤其是声音信号的方面，也常被叫做语音增强，语音增强是指当语音信号被各种各样的噪声干扰、甚至淹没后，从噪声背景中提取有用的语音信号，抑制、降低噪声干扰的技术。一句话，从含噪语音中提取尽可能纯净的原始语音。

本文会将粒子群算法改进后的LMS滤波算法与其他常用的维纳滤波算法以及谱减算法进行减噪性能比对，以此来评估算法的降噪性能。

1 LMS自适应滤波算法

1.1 MS自适应滤波基本概念

1959年，有Widrow和Hoff在研究自适应线性元素的模式识别方案时提出了LMS算法，从而奠定了自适应滤波的理论基础。之后，各种各样的自适应滤波算法相继被提出，并是自适应滤波器在跟多领域中得以更为广泛的应用和发展。如，大约1965年，来自贝尔电话实验室的Kelly首先提出把自适应滤波器用于回音消除中。同年，Widrow和其他的自斯坦福大学的合作一起发明了自适应谱线增强器，它可用于消除译码器输出端的60Hz及心电图放大器等。

LMS滤波器的基本结构,如图1所示。

根据如图1所示，该图为LMS滤波器的基本原理框图。

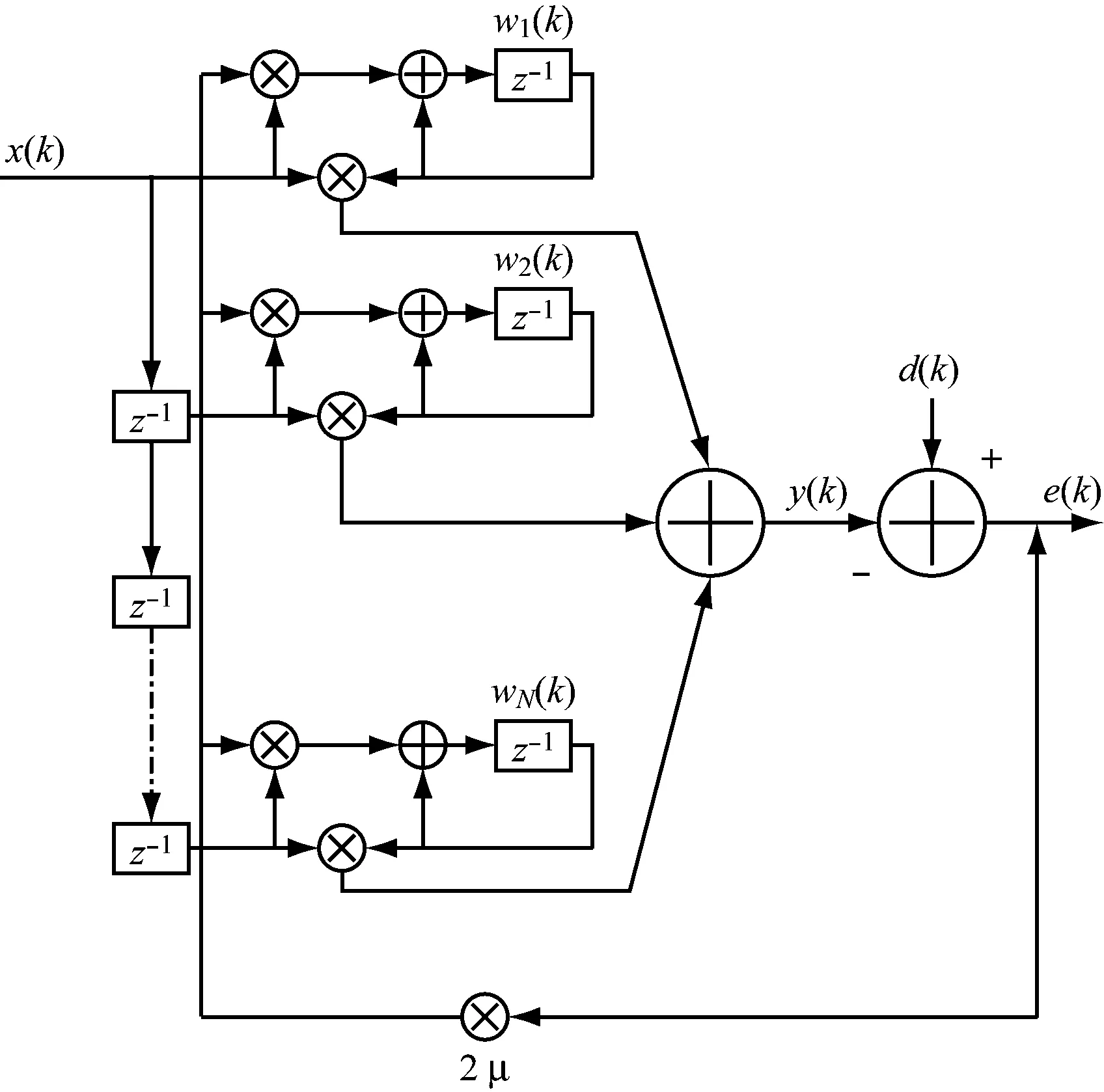
图1 LMS滤波器基本结构

初始化时，如式(1)。

w(0)=w(0)=[0 0 0 … 0]T

(1)

当k≥0时,如式(2)、式(3)。

e(k)=d(k)-xT(k)w(k)

(2)

w(k+1)=w(k)-2μe(k)x(k)

(3)

其中，(k)为瞬时的误差，μ为收敛因子，e(k)是误差信号，w(k)为的滤波器系数。按照梯度特性，w(k)在每次迭代运算中会自动调整，逐步是均值E[e2(k)]最小化，E[e2(k)]就是最小均方差。

1.2 自适应滤波在降噪中的应用

当自适应滤波被应用在降噪应用中是，它的结构框图,如图2所示。

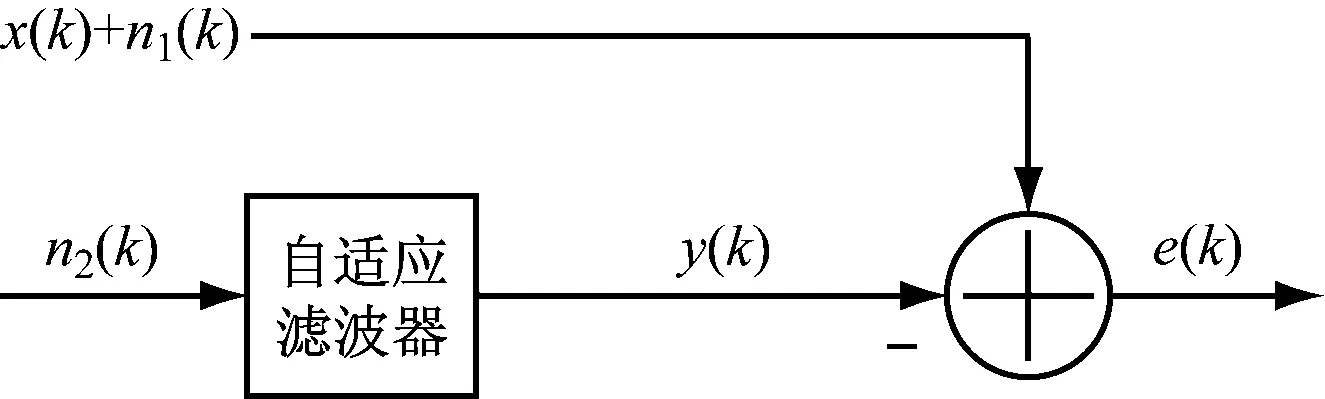
图2 信号降噪结构

与看见的自适应滤波器结构是不同的。信号x(k)受到噪声n1(k)的影响。而信号n2(k)是与噪声相关的信号，它可以被测量到的信号。n2(k)也作为自适应滤波器的输入信号，受到干扰的信号x(k)+n1(k)作为期望信号。

输出信号y(k)与输入信号n2(k)的数学关系式根据图1是式(4)

(4)

按照均方误差方程,可以得到式(5)。

E[e2(k)]=E[x2(k)]+E{[n1(k)-y(k)]2}

(5)

假如x(k)与n1(k)和n2(k)无关，那么该函数的最小MSE为式(6)。

ξmin=E[e2(k)]=E[x2(k)]

(6)

其中x(k)就是我们滤波所要得到的信号。

以该信号降噪模型和LMS基本滤波结构进行降噪滤波处理。以信噪比(Signal-Noise Ratio,SNR)评估。

收敛因子2μ=0.000 1，处理结果如下图3所示。

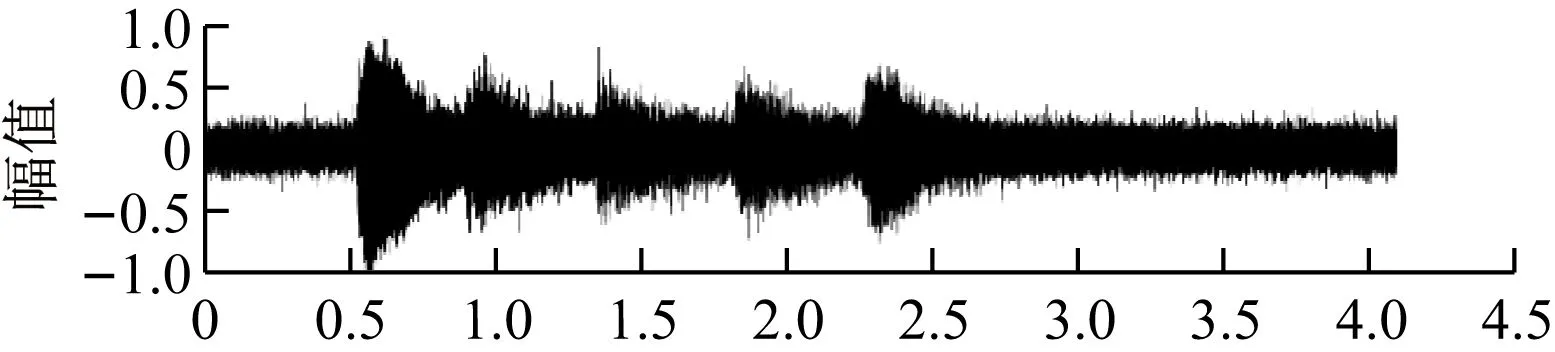
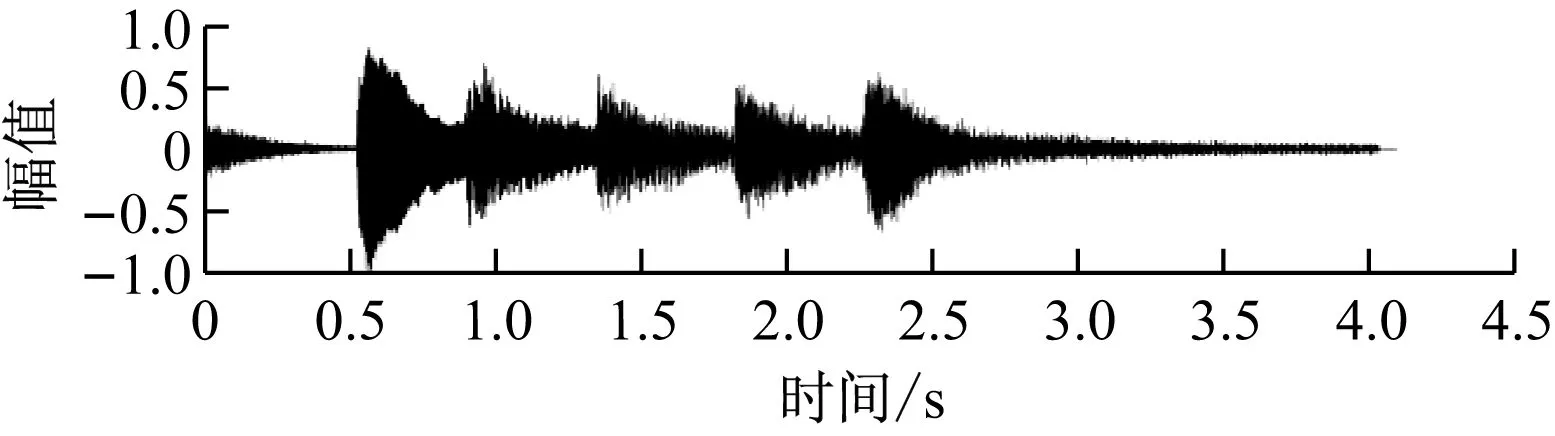
图3 普通LMS滤波效果(2μ=0.000 1)

设定带噪信号的SNR为5.0，LMS滤波后的信号的SNR为20.1。

可以很明显地看出，在使用LMS算法滤波后，噪声信号在信号的刚开始的部分仍然存在，而且噪音很大，但是后半段的信号滤波效果很好。如果提高的值，滤波信号前端噪音会有所减少，但是会造成整体的滤波效果不理想。

当收敛因子2μ=0.01，滤波效果,如图4所示。

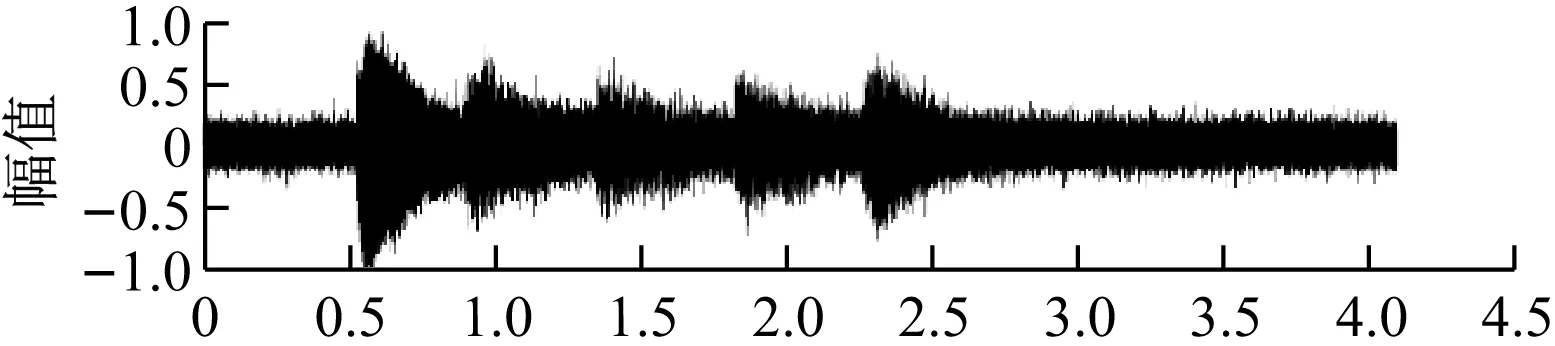
设定带噪信号SNR为5.0, LMS滤波后的信号的SNR为7.7。

可以看出,在使用LMS滤波后，前端的信号噪声消除了，但是之后的信号噪声仍然很大，说明收敛速度提升，会影响收敛的精度，滤波效果变得更差。

这就是收敛速度慢和收敛精度之间矛盾。提高收敛精度势必会造成收敛速度降慢，提高收敛速度结果造成收敛精度低。本文利用粒子群算法来解决这一矛盾。

2 粒子群算法

2.1 粒子群算法的基本概念

粒子群算法，也称粒子群优化算法(Particle Swarm Optimization)，缩写为PSO，是近年来发展起来的一种新的进化算法(Evolutionary Algorithm-EA)。PSO算法属于进化算法的一种，它是从随机解出发，通过迭代寻找最优解，它也是通过适应度来评价解的品质，但它比遗传算法规则更为简单，它没有遗传算法的“交叉”(Crossover)和“变异”(Mutation)操作，它通过追随当前搜索到的最优值来寻找全局最优。这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视，并且在解决实际问题中展示了其优越性。

假定搜索空间E内有N个粒子，i(i=1～N)对应搜索空间内一个粒子，设定粒子在该搜索空间E内对应的位置地址表示为xi=(xi1,xi2,…,xE-2,xE-1,xE)，设定粒子在该搜索空间E内的运动速度表示为vi=(vi1,vi2,…,viB,viE-1,viE)，建立所有粒子在搜索空间E内的速度和更新方程为式(7)、式(9)

vid(t+1)=ωvidI(t)+c1rand1[pid-

xid(t)]+c1rand2[pgd-xid(t)]

(7)

(8)

xid(t+1)=xid(t)+vid(t)

(9)

在式(7)中，t表示算法的迭代次数。c1和c2是加速因子(acceleration coefficient)，加速因子一般也设为恒定的常量。ω是惯性权重(inertia weight)，惯性权重一般设为一个恒定常量。pid代表粒子在之前的迭代进程中在搜索空间内最优的位置，而pgd代表当前迭代次数下粒子在搜索空间内最优的位置。通过计算pid和pgd与所有粒子现在所在位置xid(t)之差来更新接下去所有粒子在搜索空间内的速度与移动趋势，因此所有粒子能向着它现在最优位置和粒子群目前最优的位置运动。此外方程中设定了随机数rand1和rand2,它们是是在[0,1]之的随机数。通过设定随机数，从而让所有粒子更新带有一定的随机性。

基本的粒子群算法的工作流程是如下图5所示。

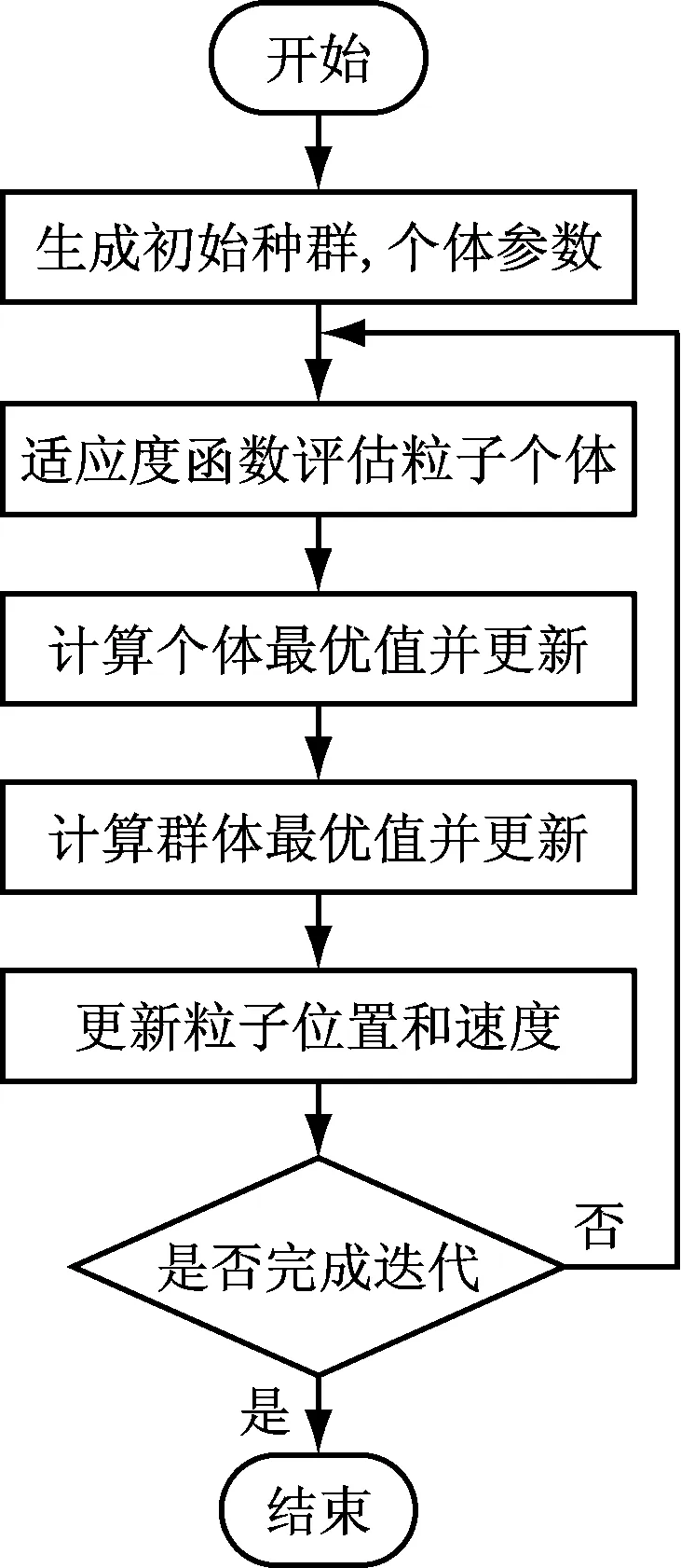
图5 粒子群算法基本流程

1)算法进入初始阶段，生成粒子群，在设定的空间范围内，对粒子的初始位置和速度赋值。

2)使用适应度函数对所有粒子进行评估值，记录个体历史上的最优值和群体中最优值。

3)根据更新方程，更新所有粒子的位置和速度。

4)判断迭代是否完成，或者达到计算的要求，如果没有完成或达到要求，转到第二步继续迭代操作。如果达到迭代上限，或者达到计算要求结束迭代。

5)输出评估出的最优结果，结束程序。

其中，适应度函数是用于评估粒子目前所在的位置。利用该函数可以评估出目前最优的粒子位置。

3 粒子群算法对LMS滤波算法的改进

式2和式3所示的更新方程是LMS算法的最重要的工作步骤。根据梯度特性E[e2(k)]会不断趋于最小均方差。其中。从式2能够推倒出下式(10)。

e(k+1)=d(k+1)-xT(k+1)[w(k)-2μe(k)x(k)]

(10)

e(k)是瞬时误差，根据式10所示，收敛因子2μ决定了E[e2(k)]的最小值。许多研究都是针对2μ，通过动态调整2μ使得E[e2(k)]值逐步达到最小，从而提高收敛性。而本文则使用粒子群算法优化能力，使得E[e2(k)]在每次迭代中做到最小化，实现LMS滤波的最优收敛效果，从而提升滤波降噪能力。

首先将收敛因子μ设为搜索空间内的粒子，那么对μ的调整操作就转换为寻找粒子在空间的最优位置。

根据式(10)，本文设定适应度函数，如下式(11)。

F=min(e(k+1))

(11)

该适应度函数能够实现瞬时误差的最小化，从而是最小均方差MSE达到最小。

本文将基于粒子群改进的LMS算法与其他滤波算法进行比对。

当使用PSO改进的LMS算法滤波是。效果如图6所示。

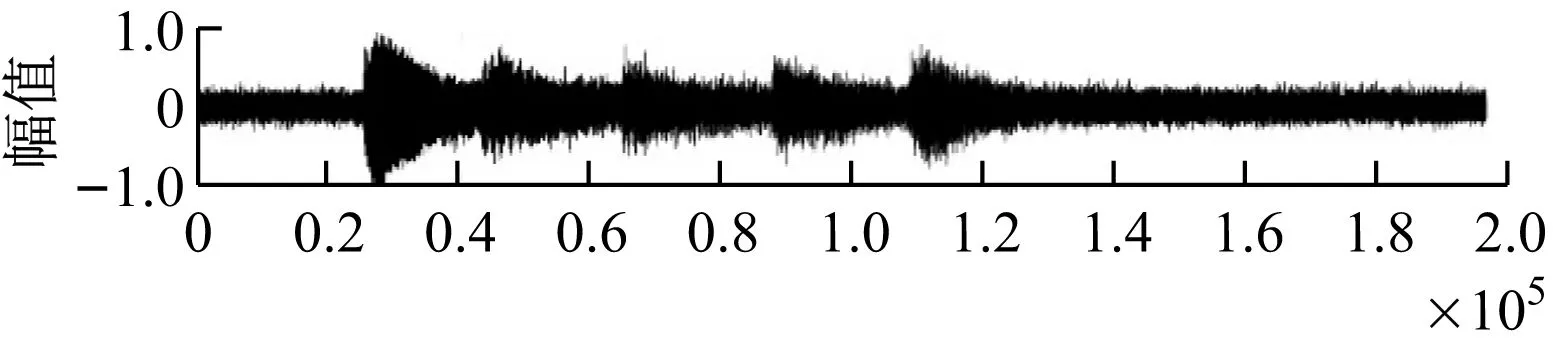
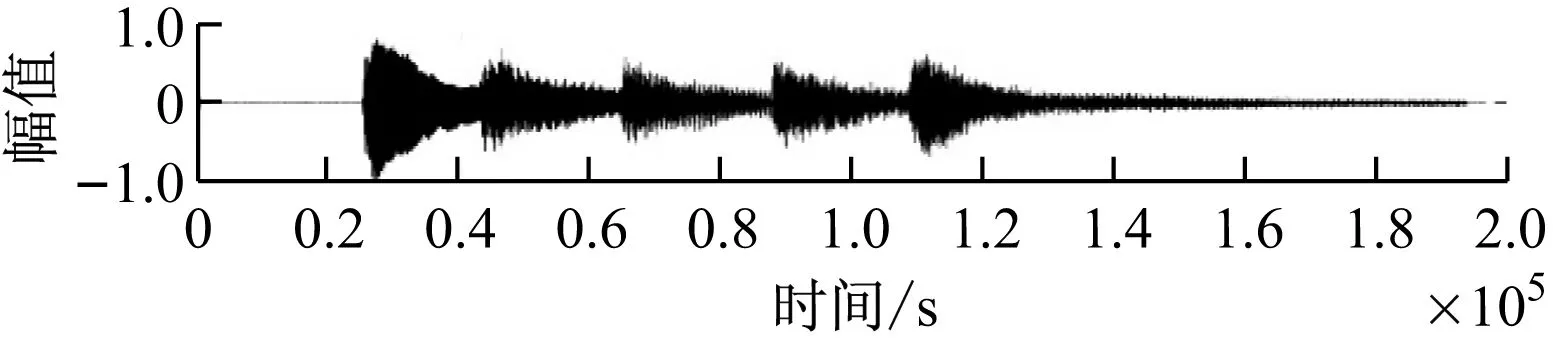
图4.1 基于PSO的LMS算法滤波效果

设定带噪信号SNR为5.0, LMS滤波后的信号的SNR为30.3。

当使用维纳滤波时，效果如图4.2所示。

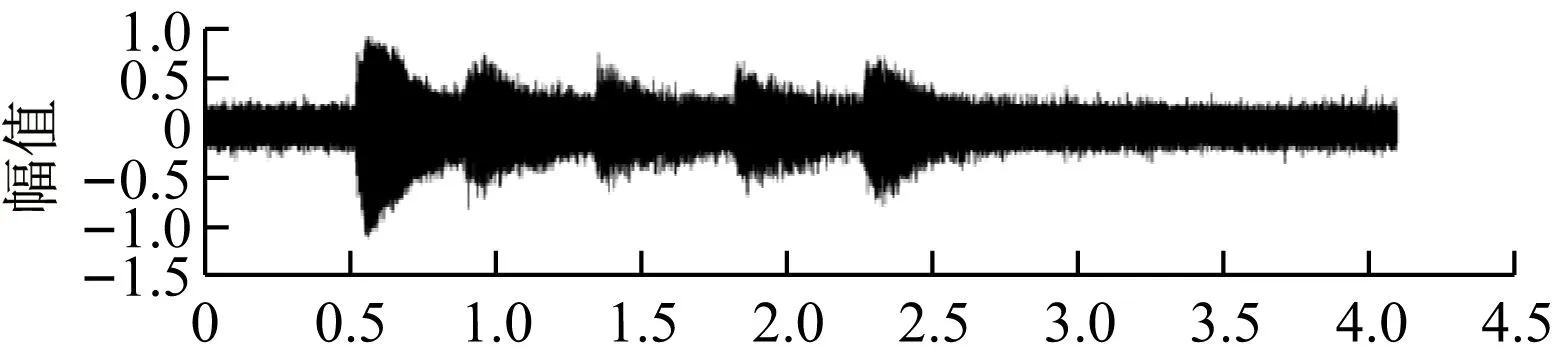
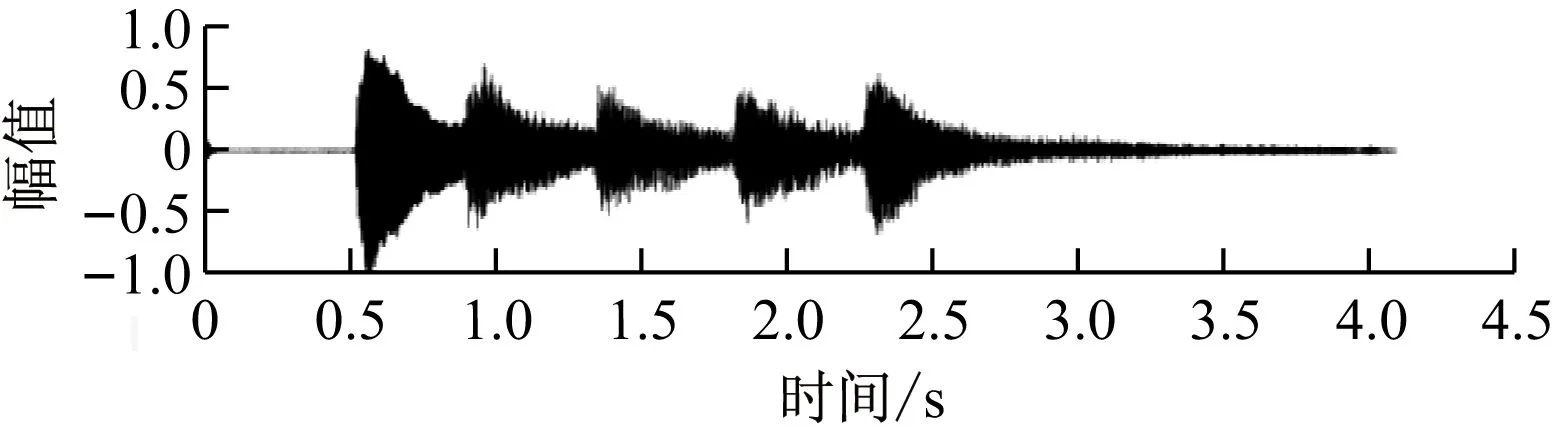
图6 维纳滤波效果

设定带噪信号的SNR为5.0，LMS滤波后的信号的SNR为17.2。

当使用谱减滤波时，效果如如图7所示。设定带噪信号的SNR为5.0，LMS滤波后的信号的SNR为14.8。

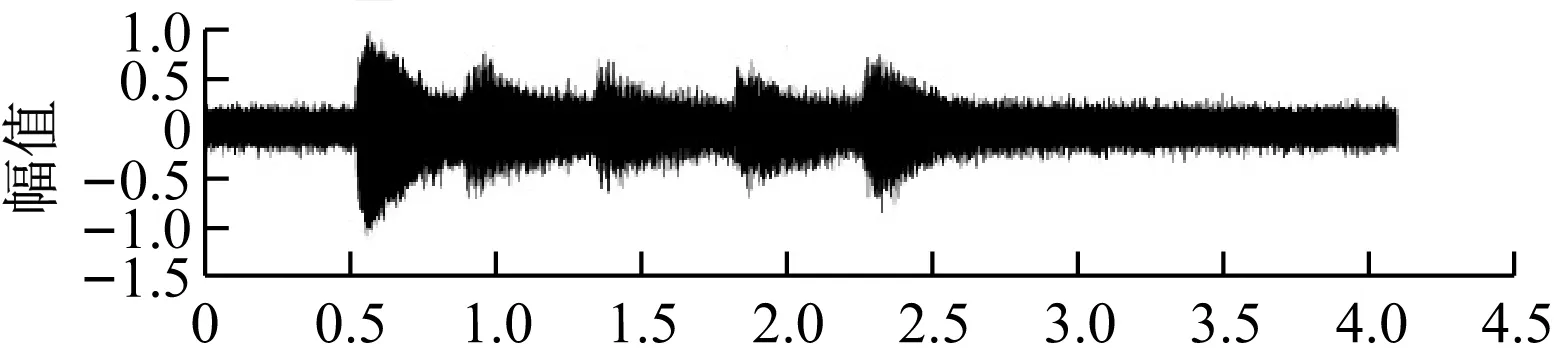
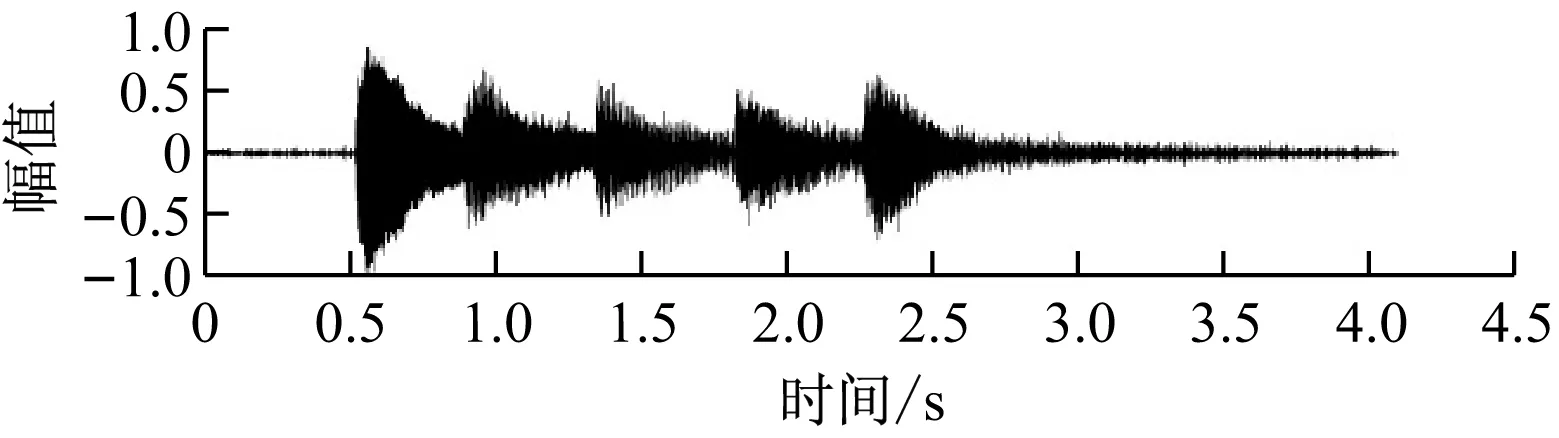
图7 谱减滤波效果

4 总结

基于PSO的LMS算法相比于其他算法，在滤波降噪上拥有更好的收敛性，更好的滤波效果。该算法能够在前期保证收敛速度，也能保证后期的收敛精度。

基于PSO的LMS算法拥有很好的收敛效果，能够有效地降低噪音信号，提取有用的信号数据。对于语音信号和音乐信号的提取还原有着非常大的作用。

[1] D. J. Krusienski, W. K. Jenkins. A Particle Swarm Optimizat ionleast Mean Squares Algorithm for Adap-

tive Filter[C]. IEEE 38th Asilomar Conference on, Signals, Systems and Computers, 2004, 1(11): 241-245.

[2] 李辉,张安,赵敏,等. 粒子群优化算法FIR数字滤器设计中的应用[J]. 电子学报, 2005, 33(7): 1338-1341.

[3] 黄媛媛,王友人,崔江,等.基于粒子群算法的自适应LMS滤波器设计及可重构硬件实现[J].佳木斯大学学报(自然科学版),2010,28(1):1-4.

[4] 吴怡.基于LMS算法的语音增强系统的研究[D]. 北京:北京邮电大学，2011.

[5] 宋智用. MATLAB在语音信号分析与合成中的应用[M]. 北京：北京航天航空大学出版社,2013.

[6] T.Mvsr, K.Meghashyam, A.Verma.Comprehensive Analysis of LMS and NLMS Algorithms using Adaptive Equalizers[C].IEEE 2014 International Conference on,Communications and Signal Processing (ICCSP), 2014,1101-1104.

[7] 迪尼. 自适应滤波算法与实现[M]. 刘郁林,译. 北京： 电子工业出版社，2014.

LMSAlgorithmBasedonPSOandApplicationintheFieldofNoise-reduceFilter

Zhao Tiexiao, Wang Lei
(Collge of Electronics and Engineering, Tongi University, Shanghai 201804, China)

TP393.04

A

2017.06.25)

赵轶骁(1990-)，男，工程硕士，研究方向：电子通信工程. 汪镭(1970-)，男，教授，研究方向:智能控制，智能计算，CIMS和系统工程方面.

1007-757X(2017)09-0071-03