基于改进模糊综合评估法大跨斜拉桥评估研究

(浙江省交通规划设计研究院, 浙江 杭州 310015)

基于改进模糊综合评估法大跨斜拉桥评估研究

邱国阳

(浙江省交通规划设计研究院, 浙江 杭州 310015)

对在役桥梁有一个合理的评估，可以为决策者提供良好的维修加固参考。针对模糊综合评估法合成算子的优缺点，提出一种新的合成算子，并采用模糊贴近度的对算法进行验证。通过对一座既有斜拉桥进行评估，证明了方法的可行性。

斜拉桥； 模糊综合评估； 模糊合成算子； 综合评估

0 引言

近年来，随着交通事业的蓬勃发展，我国修建了越来越多的大跨斜拉桥。这些桥梁的安全关系到人们日常出行及生命财产安全，在国家城市发展中起到至关重要的作用，如何对这些桥梁有一个正确的评估越来越得到学者的关注。目前桥梁综合评估的方法主要有：层次分析法、专家系统法、缺损状况指标法、灰色关联度评估法、模糊综合评估法、人工神经网络法等[1-3]。其中模糊综合评估方法能较好地解决事物的模糊性和算法的确定性这一矛盾，是对桥梁各部件及整体工作状态进行综合评估诊断的一种理想方法。在模糊综合评估法中权重的确定以及模糊合成算子一直是研究的热点，本文采用不确定AHP法确定各指标的权重向量，并提出一种新的模糊合成算子，采用“贴近度”的方法验证算子的可靠性。

1 建立桥梁综合评估模型

1.1 确定因素集

因素集即影响评判对象的各个因素，可表示为：U=[u1,u2,…,un]，ui代表各个影响因素。对于大跨斜拉桥影响其总体性能的各个因素如图1。

图1 大跨斜拉桥综合评估模型

1.2 建立评判集

评判集即确定评判因素的等级程度，无论评判目标有多少个，评判集仅有一个，设有n种判断所构成的评判集，则评判集V可表示为：V=(v1,v2,…,vn)。参考规范将桥梁工作状态划分为5个级别，设论域U=[0,100]，在U建立5个模糊集，分别为A=优级，B=良级，C=中级，D=差级，E=劣级。根据桥梁养护规范可以知道对应分数分别为88～100，60～88，40～60，20～40，0～20分。采用梯形分布函数作为隶属函数(如图2)。

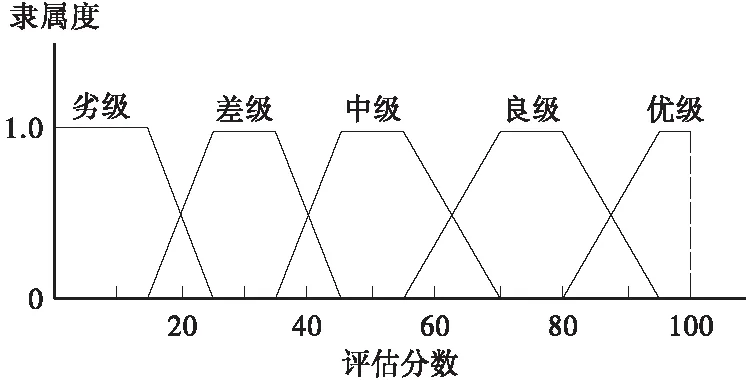
图2 大跨斜拉桥综合评估隶属函数

1.3 计算权重向量

对于因素集U=[u1,u2,…,un]，定义对于各因素ui的权重向量为：A=[w1,w2,…,wn]。权重向量采用专家讨论的方式确定。

1.4 建立模糊关系矩阵

假设有n种判断，某种判断有m个评价指标，则模糊关系矩阵R形式如下：

1.5 模糊综合评判

表1 常用模糊算子合成类型类型算子含义M(∨，∧)a∧b=min(a，b)a∨b=max(a，b)M(∗，∨)a∗b=a∗ba∨b=max(a，b)M(∧，⊕)a∧b=min(a，b)a⊕b=min(a+b，1)M(∗，⊕)a∗b=a∗ba⊕b=min(a+b，1)

模型M(∨,∧)和模型M(∧,⊕)由于首先需要进行“取大”和“取小”操作，这样就会舍去很多已有的信息，导致出现很多“盲点”。同时这2种算法将权重和指标评价的隶属度进行对比分析，将2个不同性质的物理量进行比较，会“淹没”太多的评估信息，故在桥梁综合评估中并不适用。模型M(*,∨)是一种“主因素突出型”，模型M(*,⊕)为“加权平均型”。在桥梁综合评估中既要考虑评估指标的全面性，并且也要兼顾一些特殊指标的突出性。因此本论文以“M(*,∨)算子”和“M(*,⊕)算子”为基础提出一种新的算子M(bj)。

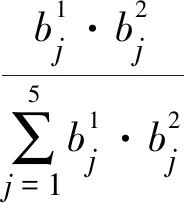
(1)

(2)

(3)

先利用公式：

(4)

(0.06,0.24,0.1,0.096,0);

(0.06,0.24,0.1,0.096,0)。

归一化可得：

根据式(1)可得：

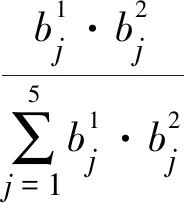
(0.025,0.799,0.113,0.063,0)

根据式(4)可得：

可见这种合成方法是比较合理的。

2 评估实例

对于底层指标评估，按照数据类型可以分为3类：①仅对桥梁构件的状态描述或进行简单的等级划分，而没有数值结果(如：砼裂缝，构件缺损等)；②检测结果为一数值(如：砼强度、保护层厚度等)；③检测结果为一数据序列(如：应力、挠度、索力等)。对第1类，采用现行有关桥梁养护规范及专家系统对缺损程度进行评价[5]；对第2类，可采用正指标、负指标和适度指标3种模型进行归一化转换；对于第3类，经过量纲归一化后，将实测数据分为均匀变化和非均匀变化两部分，采用底层指标评价值=均匀变化得分×非均匀性变化系数的形式确定其评估结果[6]。

2.1 监测指标评估

对于第1类和第2类评估指标评语集的确定比较简单，本文以浙江省某一斜拉桥监测挠度为例进行评估，说明第3类指标的评估方法。对于应力测点、挠度测点以及索力测点定义如表2评估标准[7,8]。

表2 大跨斜拉桥监测指标评估标准技术状况评定准则评分优级测点值在标准值以内88～100良级测点值在标准值和设计值之间60～88 中级测点值在设计值的110%以内40～60 差级测点值在设计值的110%～120%之间20～40 劣级测点值在设计值的120%～140%之间 0～20

1) 主梁挠度(表3)。

表3 主梁挠度评估结果测点编号监测值/mm标准值/mm设计值/mm评分1-6744-10359-145379222-3541-32474-939688673-8439-7709-1769038604-1256-123641-283757877

考虑监测数据中存在的均匀变化和非均匀变化，采用底层指标评价值=均匀变化得分×非均匀性变化系数的形式确定其评估结果，非均匀性变化系数采用灰色关联度γ(X0,Xi)进行确定，一般采用斜率关联度进行计算。

其中：

a(1)(x0(k+1))=x0(k+1)-x0(k),

k=1,2,…,n-1；

a(1)(xi(k+1))=xi(k+1)-xi(k),

k=1,2,…,N。

可以计算得到斜率关联度γ(X0,Xi)=0.95，由于各个挠度测点权重相同，则可得挠度最终评估值为：83.7分，模糊向量为(0.247，0.753，0，0，0)。

2) 主梁应力(表4)。

同理可得不均匀变化系数为：γ(X0,Xi)=0.96，可得应力评估最终得分为：84.8分，模糊向量为(0.32，0.68，0，0，0)。

表4 主梁应力评估结果测点位置应力/MPa标准值/MPa设计值/MPa评分1上缘-194-193-291877下缘22472334488842上缘-209-210-301883下缘18031854028833上缘-1445-155-369888下缘2136223596885

3) 索力(表5)。

可得不均匀变化系数为：γ(X0,Xi)=0.94，可得应力评估最终得分为：86.7分，模糊向量为(0.447，0.553，0，0，0)。

表5 斜拉索索力评估结果索号索力/kN标准值/kN设计值/kN恒载索力/kN评分15984639867375152714924248994946658421405608863405142774504443524691643458371544270629358920529013450138548269979686265127643314572129490172599292903266122417938

2.2 桥梁综合评估

针对离线指标，参考桥梁评定规范要求，采用缺损度评估方法对各构件状态进行评定。并结合本文监测指标的评估结果(见表6)，得出桥梁的综合评估结果为：V=(0.974,0.026,0,0,0)，根据最大隶属度原则可知，本斜拉桥评估结果为优级，桥梁状态良好。

表6 大跨斜拉桥综合评估结果二级指标权重评估结果综合评估主梁0221(0767，0232，0，0，0)索塔0242(1，0，0，0，0)斜拉索0312(0819，0181，0，0，0)(0974，0026，0，0，0)附属设施0201(0996，0004，0，0，0)下部结构0024(1，0，0，0，0)

3 结语

本论文对模糊综合法的模糊合成算子进行分析，提出一种新的合成算子，采用“贴近度”进行算法的验证，并对浙江省某一斜拉桥进行综合评估，验证了算法的可行性。同时针对桥梁监测数据的评估，由于规范中没有明确的规定，本论文给出详细的评估过程，为相应工程提供参考。

[1] 南宇宏，刘新，赵颂，等.既有桥梁评估方法探究[J].甘肃科技，2013，29(6):106-109.

[2] E.Zio.On the use of the analytic hierarchy process in the aggregation of expert judgments[J].Reliability Engineering and System Safety,1996,53:127-138.

[3] HitoshiFuruta,Jianhong He, EiichiWatanabe. A Fuzzy Expert System for Damage Assessment Using Genetic Algorithms and Neural Networks [J]. Journal of Computing in Civil Engineering,1996, 11: 37-45．

[4] 宋光兴，杨德礼.基于决策者偏好及赋权法一致性的组合赋权法[J].系统工程与电子技术，2004，26(9)：1226-1230，1290.

[5] JTG H11-2004，公路桥涵养护规范[S].

[6] 兰海，史家钧.灰色关联分析与变权综合法在桥梁评估中的应用[J].同济大学学报，2001，29(1)：50-54.

[7] 任远，黄侨，李辉.大跨度斜拉桥的综合评估理论体系研究[A]. 全国既有桥梁加固、改造与评价学术会议论文集[C].2008.

[8] 李毅.基于城市桥梁集群监测平台的系杆拱桥健康监测研究[D].杭州：浙江大学，2010.

1008-844X(2017)03-0135-04

U 448.27

A

2016-11-17

浙江省交通运输厅科研计划项目(2015B04)

邱国阳(1979-)，男，高级工程师 ，从事桥梁试验检测工作。