直孔掏槽一次成井的改进TOPSIS-CV掏槽方式评价模型

刘恺，李夕兵，李启月，王泽伟，谢晓锋



直孔掏槽一次成井的改进TOPSIS-CV掏槽方式评价模型

刘恺，李夕兵，李启月，王泽伟，谢晓锋

(中南大学资源与安全工程学院，湖南长沙，410083)

为了解决直孔掏槽一次成井中掏槽方式选择的难题，通过引入逼近理想解技术(TOPSIS)，并将垂面距离代替欧氏距离的正交投影法和传统TOPSIS相结合，提出一种基于改进TOPSIS法的综合评价模型。从安全、技术、经济3个方面综合考虑选取了7个评价指标，利用变异系数法(CV)确定指标权重，避免主观权重赋值法的人为因素干扰，使得权重赋值更加客观化。将该评价模型应用于某矿山一次成井治理采空区试验中，对初步设计的4种掏槽方式进行综合评价，并将最佳的掏槽方式用于工业试验。研究结果表明：计算出每个方案到正理想解的垂面距离分别为0.125 94，0.089 89，0.060 40，0.041 53，从而确定第4种方案为最优方案。与传统的TOPSIS法评价结果相比，改进的TOPSIS法评价结果的优劣程度更加明显，更加容易甄选出最佳方案。由最佳方案形成的天井上下贯通，达到设计规格，效果较好。

一次成井；掏槽方式；综合评价模型；改进TOPSIS法；变异系数法

天井掘进广泛应用于国防和民用工程当中。传统的普通法、吊罐法和爬罐法等天井掘进方法由于掘进速度慢，施工环境恶劣，安全系数低，成本高等缺点，已逐渐被淘汰[1]。起源于地下采矿VCR法的直孔掏槽一次成井技术具有安全、高效、低成本等优点，从而成为重点研究和推广应用的对象[2]。由前人的研究[3−4]可知，槽腔形成的大小是爆破一次成井成功与否的关键因素，而掏槽方式的选择决定着槽腔的形状和尺寸。传统的掏槽方式的设计一般由设计者根据现场试验和主观经验来确定，受主观影响较大。一方面，掏槽试验存在场地限制、试验成本高、耗时久、试验组数难以保证可靠度等问题。另一方面，槽腔的形成受岩体性质、孔偏率、掏槽参数等多种客观因素的影响，仅用经验或少量试验设计方法往往达不到最优设计的目的，因此需要一种客观可靠的，并考虑多因素的评价选取方法。直孔掏槽一次成井掏槽方式的评价选取是一个涉及多因素、多目标的决策过程，对此，逼近理想解技术(TOPSIS)具有较大优势。TOPSIS法已在矿井通风系统评价[5−6]、采矿方法优选[7−8]、岩爆预 测[9−10]、岩体质量评价[11]等领域运用广泛，如吴立云等[6]建立了基于熵权的多层次TOPSIS评价模型对矿井通风系统进行评价；王新民等[8]建立了AHP− TOPSIS综合评判模型，选择最佳采矿方法，解决了驻留矿体的开采难题；龚剑等[9]选取了多种评价指标，验证了AHP−TOPSIS评价模型在岩爆预测中应用的可行性；胡建华等[11]将TOPSIS法和粗糙集理论相结合，对地下岩体工程进行评价。然而上述研究中都是采用欧式距离作为计算方案到正理想解贴近度依据的传统TOPSIS法，其存在排序模糊导致评价失真的可能性，为此本文作者引入垂面距离代替欧式距离，采用正交投影法对传统的TOPSIS法进行改进。同时针对层次分析法、专家打分法等主观赋权法存在受决策者主观影响较大的缺点，利用客观权重赋值法—变异系数法(CV)确定指标权重。并将改进的TOPSIS法应用于直孔掏槽一次成井的掏槽方式优选中，为一次成井掏槽方式的选取提供新的路径。

1 变异系数法确定评价指标权重

变异系数法中权重的确定完全取决于指标数据本身的特点，不受决策者主观影响，具有客观性[12−13]。同时，变异系数法将评价指标的变异程度作为确定指标权重的依据，权重随着指标动态变化，因此，变异系数法是一种客观、动态的权重赋值法。若评价指标集，中某个指标h在待评价方案集，中变化范围较大，则该指标对待评价方案的优劣排序影响较大，反之，当指标h在待评价方案集中变化范围较小时，则该指标对待评价方案的优劣排序影响较小，其中当所以待评价方案的指标h相同无变化时，该指标对评价结果没有影响。因此，通过改变指标的变化范围，采用变异系数法确定指标权重。具体步骤为：

1) 构造评价指标的特征值矩阵(TOPSIS法中决策矩阵)：

式中：h为第个待选方案中第个指标的值。计算第项指标的平均值：

(2)

2) 计算第项指标的均方差：

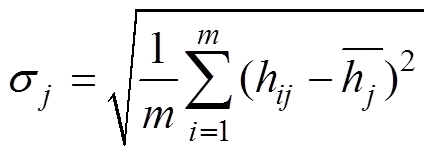
则第项指标的变异系数：

(4)

3) 第项指标的权重为

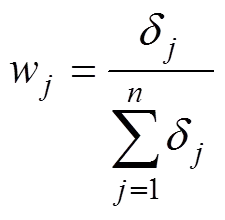
2 改进TOPSIS法掏槽方式评价模型

2.1 TOPSIS法基本原理

TOPSIS法由HWANG等[14]提出，解决了多目标决策问题。其基本原理为：在TOPSIS评价模型中，假设评价方案存在一个正理想解(最佳方案，方案内的所有评价指标都为最优值)和负理想解(最差方案，方案内的所有评价指标都为最差值)，通过评价方案到正负理想解的欧氏距离，计算出评价方案与正理想解的贴近度，然后根据贴近度对方案进行排序，若评价方案既离正理想解最近，又离负理想解最远，则该方案最佳，反之，方案最差。

传统的TOPSIS法采用欧式距离作为计算与正理想解的贴近度的依据，其中存在一个不容忽视的缺陷：在多个评价方案中，与正理想解欧氏距离更近的方案可能与负理想解的欧氏距离也更近，因此其评价结果不能完全反映方案之间的优劣性[15]。假设某评价体系中含有2个评价指标1和2，(1A，2A)，(1B，2B)，(1C，2C)和(1D，2D)分别为4个评价方案A，B，C和D的样本点，(，)和(，)分别为评价方案的正、负理想解，其中，连线、连线都为连线的垂线，如图1所示。采用传统的TOPSIS法评价，评价方案到正理想解的贴近度为

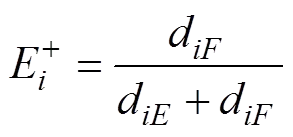
图1 垂面距离示意图

Fig. 1 Schematic diagram of vertical distance

2.2 改进的TOPSIS法

引进垂面距离代替欧式距离，采用正交投影法来计算垂面距离反映评价方案的贴近度，根据方案与正理想解的垂面距离来评价方案。垂面距离为在正负理想解连线两边存在点和，以为法向量，分别过点和作平面和，和之间的距离即为垂面距离。如图1所示，方案A和方案D在直线上的投影分别为和，因此方案A和方案D之间的垂面距离为点和之间的欧氏距离，也就是平面和之间的距离。

由垂面距离可知：方案A和方案B到正理想解的垂面距离相等为d，因此方案A和方案B具有相同的排序，同理可得方案C和方案D也具有相同排序。垂面距离的引入解决了欧式距离可能存在的排序不清的缺陷。

2.3 TOPSIS评价模型建立步骤

1) 建立直孔掏槽一次成井掏槽方式评价指标体系。直孔掏槽一次成井的掏槽方式选择受多个因素的影响和制约，主要分为安全、技术、经济3个方面。本文根据前人的研究和现场生产资料确定了方案实施难易(1)、槽腔横截面面积(2)、空孔数(3)、限制孔偏率(4)、成井高度(5)、炸药单耗(6)和天井掘进成本(7)共7个评价指标。

2) 变异系数法确定各指标权重。采用变异系数法计算出指标权重向量

3) 建立标准化决策矩阵。为了消除指标之间不同量纲的影响，对指标的特征值矩阵进行标准化处理，得到标准化决策矩阵。

对于效益型指标：

对于成本型指标：

(8)

式中：P为指标标准化处理后的值，max(h)为第项指标中的最大值，min(h)为第项指标中的最小值。

因此标准化决策矩阵为

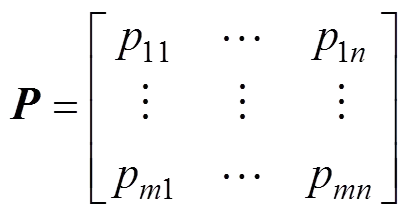
4) 建立加权决策矩阵。由标准化决策矩阵的每一列指标和权重向量中对应的指标权重相乘，得到加权决策矩阵：

(10)

5) 计算正理想解+和负理想解­。

式中：1为效益型指标集；2为成本型指标集。

6) 计算待评价方案的垂面距离。

设图1中，，，，的向量分别为，，，，则和的垂面距离为

(13)

式中：和分别为平移后的正、负理想解；为平移矩阵的第行向量。

7) 计算出每个待评价方案到正理想解的垂面距离d后，根据d进行排序，d越小，表示该方案越接近正理想解，方案越优，反之，则方案越差。

3 工程实例

某矿山经过30多年的地下开采，在露天开采境界内形成了大量的地下空区，共有空区体积2 000万m3，地下所有的空区均未进行充填，空区形态不规则、大小高低不一致，空区顶板连续暴露面积大，上下空区重叠交错，空区间隔层薄，甚至几层相互贯通，形态极其复杂，既危及企业生产安全，也限制大型设备使用，还扰乱企业生产组织，同时也降低了劳动生产效率和提高了生产经营成本。矿山原采用地表碎石充填与地表块石充填为主的处理采空区方案。但由于地表碎石充填孔径较小，充填效率较慢，空区治理周期较长，且需要对次品矿进行破碎，成本较高。为此，提出并设计直孔掏槽爆破一次成井块石充填技术处理采空区的试验方案，本文就直孔掏槽爆破成井的掏槽方式进行评价，优选出最佳掏槽方式。

3.1 待评价掏槽方式

根据采空区的形态特征、地质条件和现有施工技术，设计了4种掏槽方式进行综合评价，分别为单空孔螺旋掏槽、3空孔菱形掏槽、4空孔桶形掏槽和5空孔桶形掏槽，如图2所示，其评价指标见表1。

表1 各方案的评价指标值

3.2 变异系数法计算指标权重

从而可求得指标权重向量=(0.14，0.105，0.282，0.1578，0.173 5，0.069，0.072 7)。

3.3 改进TOPSIS法计算评价方案垂面距离

根据式(7)和式(8)将指标量纲一化，建立标准化决策矩阵：

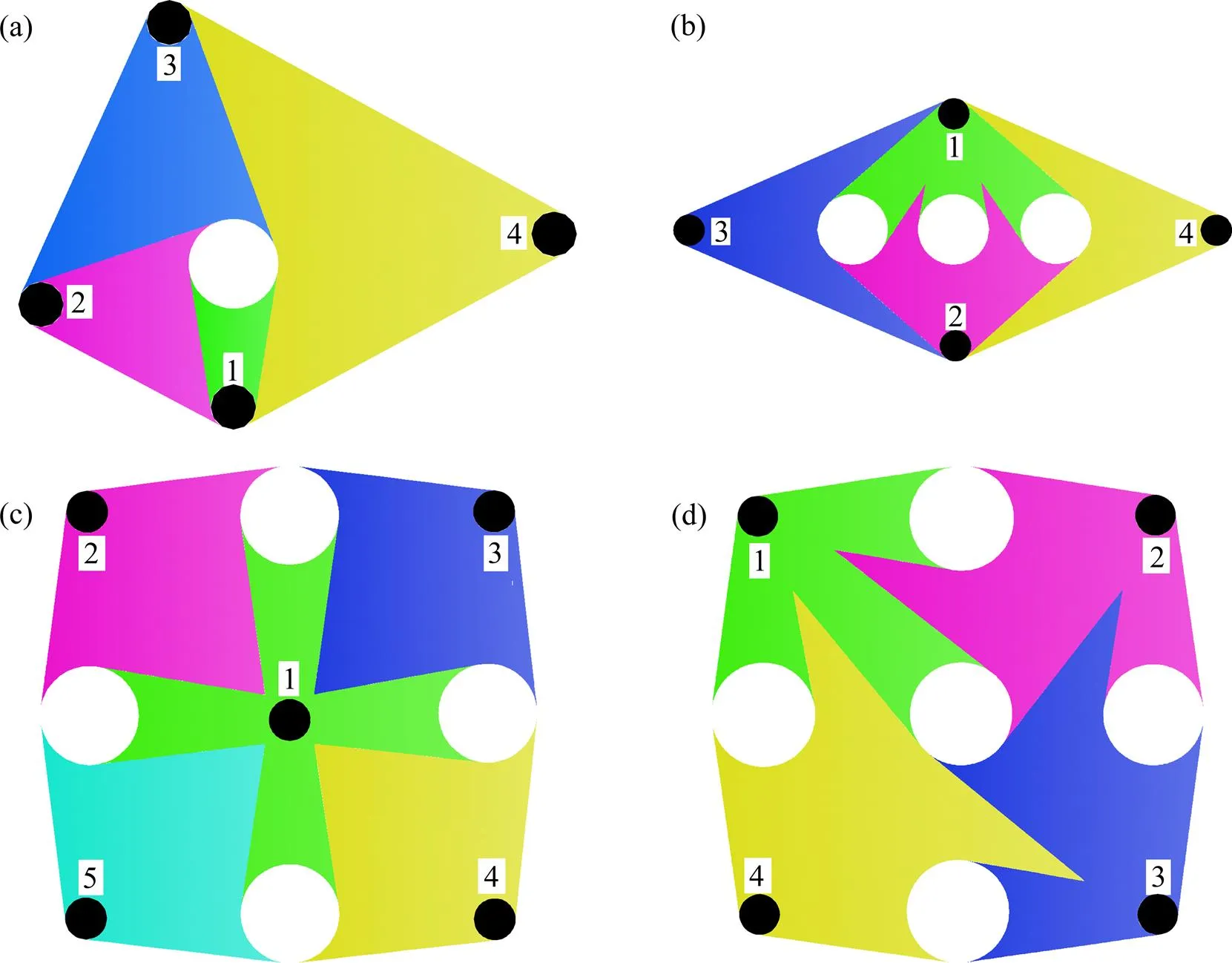
(a) 单孔螺旋掏槽；(b) 3空孔菱形掏槽；(c) 4空孔桶形掏槽；(d) 5空孔桶形掏槽

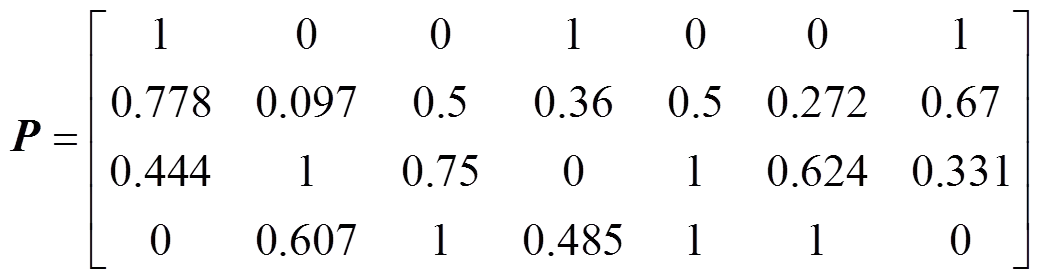
将矩阵中每项指标与其对应的权重相乘，得到加权决策矩阵：

指标1~5为效益型指标，指标6~7为成本型指标，因此方案的正理想解为：

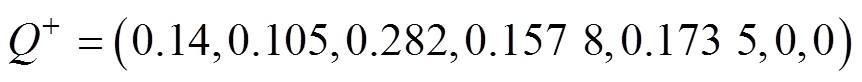
将正理想解移至坐标原点，得到平移矩阵：

根据式(13)计算出4个方案到正理想解的垂面距离分别为1=0.125 94，2=0.089 89，3=0.060 40，4=0.041 53。

3.4 评价结果分析

根据4个方案的垂面距离可知，方案的优劣程度从高到低为方案4、方案3、方案2、方案1，因此方案4的5空孔桶形掏槽最接近理想方案，为最优方案。

传统的TOPSIS法评价，得出4个方案的综合优越度分别为0.386 5， 0.486 1，0.606 0，0.659 3。将改进TOPSIS法和传统TOPSIS法的评价结果按照式(7)和式(8)进行量纲一化比较，其比较结果如表2所示。

表2 改进TOPSIS法和传统TOPSIS法评价结果比较

由表2可知：虽然传统TOPSIS法与改进TOPSIS法得到的方案优劣排序一致，但是改进的TOPSIS法能更加明显的区分方案之间的优劣程度，凸显出最佳方案的优越性，更加容易判断选择出最佳方案。

矿山采用5空孔桶形掏槽方式进行爆破一次成井试验，成井效果良好，规格达到设计要求，通过天井对采空区进行充填，消除了采空区对矿山正常生产的安全隐患，成功治理了矿山采空区。

4 结论

1) 建立了改进的TOPSIS法一次成井掏槽方式评价模型，该模型将传统TOPSIS法采用的欧式距离替换成垂面距离，弥补了传统TOPSIS法存在的排序模糊不清，方案优劣性不明显等不足，使得评价结果更加客观、科学。

2) 利用变异系数法确定指标权重，充分地挖掘、利用原始数据，尊重客观实际，避免了指标权重分配受决策人的主观意志和个人经验的影响，得到了更为符合客观实际的指标权重。

3) 采用改进的TOPSIS评价模型对一次成井的4个待选掏槽方案进行评价，计算出了每个方案的垂面距离，其中方案4的垂面距离最小，最接近正理想解，因此确定方案4为最优方案，并将其应用于一次成井试验中，获得了良好的效果。

[1] 李启月, 李夕兵, 范作鹏, 等. 深孔爆破一次成井技术与应用实例分析[J]. 岩石力学与工程学报, 2013, 32(4): 664−670. LI Qiyue, LI Xibing, FAN Zuopeng, et al. One time deep hole raise blasting technology and case study[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 664−670.

[2] 袁再武. 我国天井掘进技术现状[J]. 长沙矿山研究院季刊,1985, 5(1): 37−43. YUAN Zaiwu. The status of raise excavation in China[J]. Quarterly of Changsha Institute of Mining Research, 1985, 5(1): 37−43.

[3] 赵国彦, 赵井清, 李启月. 9孔桶形掏槽一次成井技术[J]. 科技导报, 2013, 31(16): 21−25. ZHAO Guoyan, ZHAO Jingqing, LI Qiyue. Nine-hole parallel cutting technology of the shaft excavation in one-step[J]. Science and Technology Review, 2013, 31(16): 21−25.

[4] STERK P V. Development of drop raise blasting at Homestake mine[C]// Proceedings of the 17th Annual Conference on Explosives and Blasting Technique. Las Vegas, NE: International Society of Explosive Engineers, 1991: 239−250.

[5] 董宪伟, 蔡嗣经, 杨鹏, 等. 矿井通风系统优化方案评价的逼近理想解方法[J]. 煤炭科学技术, 2008, 36(8): 58−61.DONG Xianwei, CAI Sijing, YANG Peng, et al. Approximated ideal explanation method for assessment on optimized plan of mine ventilation system[J]. Coal Science and Technology, 2008, 36(8): 58−61.

[6] 吴立云, 杨玉忠, 张强. 矿井通风系统评价的TOPSIS方法[J]. 煤炭学报, 2007, 32(4): 407−410. WU Liyun, YANG Yuzhong, ZHANG Qiang. TOPSIS method for evaluation on mine ventilation system[J]. Journal of China Coal Society, 2007, 32(4): 407−410.

[7] 赵国彦, 唐洋, 刘志祥, 等. 基于改进的AHP-TOPSIS评判模型的盛大铁矿采矿方法优选[J]. 科技导报, 2013, 32(3): 25−28. ZHAO Guoyan, TANG Yang, LIU Zhixiang, et al. Mining method optimization of Shengda iron ore based on improved AHP-TOPSIS evaluation model[J]. Science and Technology Review, 2013, 32(3): 25−28.

[8] 王新民, 秦健春, 张钦礼. 基于AHP-TOPSIS评判模型的姑山驻留矿采矿方法优选[J]. 中南大学学报(自然科学版), 2013, 44(3): 1131−1137. WANG Xinmin, QIN Jianchun, ZHANG Qinli. Mining method optimization of Gu Mountain stay ore based on AHP-TOPSIS evaluation model[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1131−1137.

[9] 龚剑, 胡乃联, 崔翔. 基于AHP-TOPSIS评判模型的岩爆倾向性预测[J]. 岩石力学与工程学报, 2014, 33(7): 1142−1148. GONG Jian, HU Nailian, CUI Xiang. Rockburst tendency prediction based on AHP-TOPSIS evaluation model[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(7): 1142−1148.

[10] 周科平, 雷涛, 胡建华. 深部金属矿山RS-TOPSIS岩爆预测模型及其应用[J]. 岩石力学与工程学报, 2013, 32(增2): 3705−3711. ZHOU Keping, LEI Tao, HU Jianhua. RS-TOPSIS model of rockburst prediction in deep metal mines and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(s2): 3705−3711.

[11] 胡建华, 尚俊龙, 雷涛. 基于RS-TOPSIS法的地下工程岩体质量评价[J]. 中南大学学报(自然科学版), 2012, 43(11): 4412−4419. HU Jianhua, SHANG Junlong, LEI Tao. Rock mass quality evaluation of underground engineering based on RS-TOPSIS method[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4412−4419.

[12] 刘培德, 关忠良. 属性权重未知的连续风险型多属性决策研究[J]. 系统工程与电子技术, 2009, 31(9): 2133−2136. LIU Peide, GUAN Zhongliang. Research on multiple attribute decision-making under risk with continuous random variable and weight unknown[J]. Engineering and Electronics, 2009, 31(9): 2133−2136.

[13] 何美丽, 刘浪, 王宏伟, 等. 基于集对分析的工程评标未知权重多属性决策[J]. 中南大学学报(自然科学版), 2012, 43(10): 4057−4062. HE Meili, LIU Lang, WANG Hongwei, et al. Unknown weight multiple attribute decision for engineering appraisal bidding based on set pair analysis[J]. Journal of Central South University (Science and Technology), 2012, 43(10): 4057−4062.

[14] HWANG C L, YOON K. Multiple attribute decision making methods and applications[M]. Berlin: Springer, 1981.

[15] YUE Z L. An extended TOPSIS for determining weights of decision marks with interval numbers[J]. Knowledge-Based Systems, 2011, 24(1): 146−153.

[16] 肖淳, 邵东国, 杨丰顺. 基于改进TOPSIS法的流域初始水权分配模型[J]. 武汉大学学报(工学版), 2012, 45(3): 329−334. XIAO Chun, SHAO Dongguo, YANG Fengshun. A model of initial water rights allocation in watershed based on improved TOPSIS method[J]. Engineering Journal of Wuhan University, 2012, 45(3): 329−334.

[17] 屈吉鸿, 陈南祥, 黄强, 等. 改进的逼近理想解在地下水资源承载力评价中的应用[J]. 水利学报, 2008, 39(12): 1309−1314. QU Jihong, CHEN Nanxiang, HUANG Qiang, et al. Improved TOPSIS method for evaluating groundwater carrying capacity[J]. Journal of Hydraulic Engineering, 2008, 39(12):1309−1314.

[18] 徐存东, 翟东辉, 张硕, 等. 改进的TOPSIS评价模型在河道整治方案优选中的应用[J]. 河海大学学报(自然科学版), 2013, 41(3): 222−228. XU Cundong, ZHAI Donghui, ZHANG Shuo, et al. Application of improved TOPSIS comprehensive evaluation model to optimization of river regulation schemes[J]. Journal of Hohai University (Natural Sciences), 2013, 41(3): 222−228.

(编辑 赵俊)

Improved TOPSIS-CV method of cut blasting mode evaluation in one-step raise excavation with burn cut

LIU Kai, LI Xibing, LI Qiyue, WANG Zewei, XIE Xiaofeng

(School of Resources & Safety Engineering, Central South University, Changsha 410083, China)

In order to optimize cylinder cut blasting mode for one-step raise excavation, an improved TOPSIS comprehensive evaluation model combining vertical projection approach was developed. Seven indexes considering the economy, technology and security were used, and the index weights were determined by coefficient of variance method to avoid the subjectivity. The improved evaluation model was applied to goaf dealing in a mine. Finally, the optimal scheme was applied in an industrial test. The results show that the best vertical distances between the scheme and positive of the four cutting modes were calculated and were 0.125 94, 0.089 89, 0.060 40 and 0.041 53 respectively, which indicate that the fourth scheme is optimal. Compared with the traditional TOPSIS, the improved TOPSIS tends to reveal clearer differences between schemes, which is convenient to optimize the scheme. The formed raise by optimal scheme is through up and down completely, and reaches the expected size.

one-step raise excavation; cutting mode; comprehensive evaluation model; improved TOPSIS method; coefficient of variance

10.11817/j.issn.1672-7207.2017.09.029

TD236

A

1672−7207(2017)09−2484−07

2016−09−04；

2016−12−18

国家自然科学基金资助项目(51374243)；中南大学博士研究生自主探索创新项目(2017zzts186) (Project(51374243)supported by the National Natural Science foundation of China; Project(2017zzts186) supported by the Cultivating Excellent PhDs of Central South University)

刘恺，博士研究生，从事非煤矿山采矿方法、岩土工程爆破、岩石力学等研究；E-mail: lkeason@csu.edu.cn