不同形状砂岩的动态力学特性

谢晓锋，陶明，吴秋红，王泽伟，尚雪义，刘恺



不同形状砂岩的动态力学特性

谢晓锋，陶明，吴秋红，王泽伟，尚雪义，刘恺

(中南大学资源与安全工程学院，湖南长沙，410083)

为研究横截面形状对岩石试样动态力学特性的影响，采用改进后的霍普金森压杆(SHPB)对砂岩圆柱试样、方形试样和厚壁圆筒试样进行冲击试验。研究结果表明：这3种试样的动态强度均随应变率的增大而增大，由于厚壁圆筒试样存在较大自由面，故其比圆柱试样和方形试样对应变率变化更敏感；横截面形状对岩石变形模量的影响较小，而对峰值应变的影响较大，峰值应变的应变率效应不明显；横截面形状和应变率对试样破坏形式的影响较明显，方形试样棱角处均出现明显的剪切面，应变率越大，试样破碎块度越小。

岩石力学；霍普金森压杆(SHPB)；动态性质；形状效应；应变率；强度

现代工程岩体常受到爆破振动和机械扰动等动载荷的影响，对此，许多学者采用不同的方式研究中高应变率对岩石力学特性的影响[1−4]。宫凤强等[3]分析了围压对砂岩动态冲击性能的影响，并讨论了冲击过程中岩石的破坏模式。LI等[5]对岩石在动静组合加载下的力学特征进行了研究。周子龙等[6]采用真三轴试验设备对花岗岩试样进行了多种轴向静载和侧向扰动作用下的破坏试验。研究发现岩石在中高应变率下的力学特性与准静态加载下有着显著的差别，其动态力学性质也常常受到许多因素的影响，试样的形状和尺寸便是主要影响因素之一。岩石的形状多种多样，并不是单一的圆形横截面，同一岩块上不同位置点的力学特性可能存在差异[7−8]。然而，以往对形状效应的研究集中在圆形截面下不同长径比对试样力学性能的影响，如李夕兵[9]采用SHPB设备对相同直径、不同长度的圆柱石灰岩进行了冲击试验，洪亮等[10]采用相同长度、不同直径的3种岩石进行了动态力学性质研究。OLSSON等[11−13]研究了不同长径比下岩石的动态强度变化情况，发现长径比对试样的动态抗压强度没有明显的影响。目前，人们对相同高径比下不同横截面形状对岩石动态力学特性的影响研究很少，大部分都是对金属类材料进行研究。LINDHOLM等[14]认为金属材料的动态性能应该考虑形状效应的影响；AHMAD等[15−16]通过试验和数值模拟研究了金属试样长度和直径对强度的影响；SEN等[17]推导了考虑形状效应的惯性公式，发现长度和横截面形状对金属试样的动态应力应变曲线基本没有影响。然而，实际岩体并不全是实心圆形截面，因此，研究横截面形状对岩石动态力学特性的影响具有理论意义和实际意义。为此，本文作者从同一块砂岩上加工圆柱试样、方形试样和厚壁圆筒试样，研究横截面形状对岩石动态力学特性的影响。

1 静载试验

1.1 试样特征

试验用砂岩产自四川省隆昌县，呈灰色，主要矿物成分为石英和长石，无肉眼可见缺陷。试样从同一块完整砂岩中钻取，圆柱试样直径为38 mm，方形试样边长为34 mm，厚壁圆筒试样外径为48 mm、内径为16 mm，3种试样的高度均为34 mm，分别用编号Y，F和H表示。试样端面不平整度小于0.05 mm，制备后在室内自然干燥7 d，视密度为2.315~2.396 t/m3，均值为2.360 t/m3，离散系数为1.04%，纵波波速为2.556~3.238 km/s，均值为2.805 km/s，离散系数为6.68%，可见砂岩试样的均质性较好。

1.2 试验结果

为了与冲击载荷下的动态力学特性进行对比，首先对试样进行单轴压缩静载试验，仪器为SAW−2000微机控制电液伺服岩石力学试验机。采用轴向变形控制方式，加载速率为0.01 mm/s。

图1所示为部分试样单轴压缩应力−应变全程曲线，表1所示为实验结果(其中，弹性模量指峰值前应力−应变曲线中近似直线部分的斜率，变形模量指峰值应力50%处的切线斜率)。从图1可以看出：单轴压缩时试样经历了压密、弹性、屈服和破坏4个阶段，其中压密阶段变形很大，说明试样内部存在许多初始裂隙，峰值后应力跌落较快，表现出明显的脆性特征。

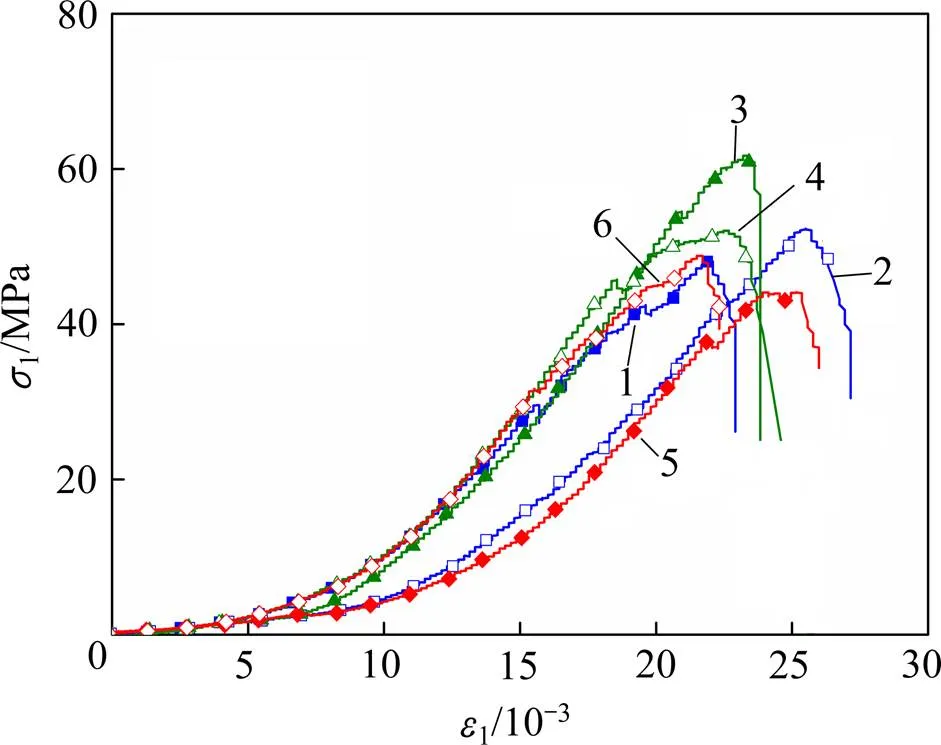
试样：1—Y1；2—Y2；3—F1；4—F2；5—H1；6—H2

圆柱试样、方形试样和厚壁圆筒试样的平均强度分别为52.4，55.8和47.7 MPa；弹性模量均值分别为4.1，4.7和4.0 GPa。圆柱试样与方形试样强度差别不大，厚壁圆筒试样强度较低，比圆柱试样强度低9%。这是因为厚壁圆筒试样存在较大的自由面，有助于岩石局部变形、屈服，而3种试样的弹性模量相差不大。

根据静态试验结果可知，较大的孔洞对其强度影响较大，而试样形状对弹性模量没有明显影响。

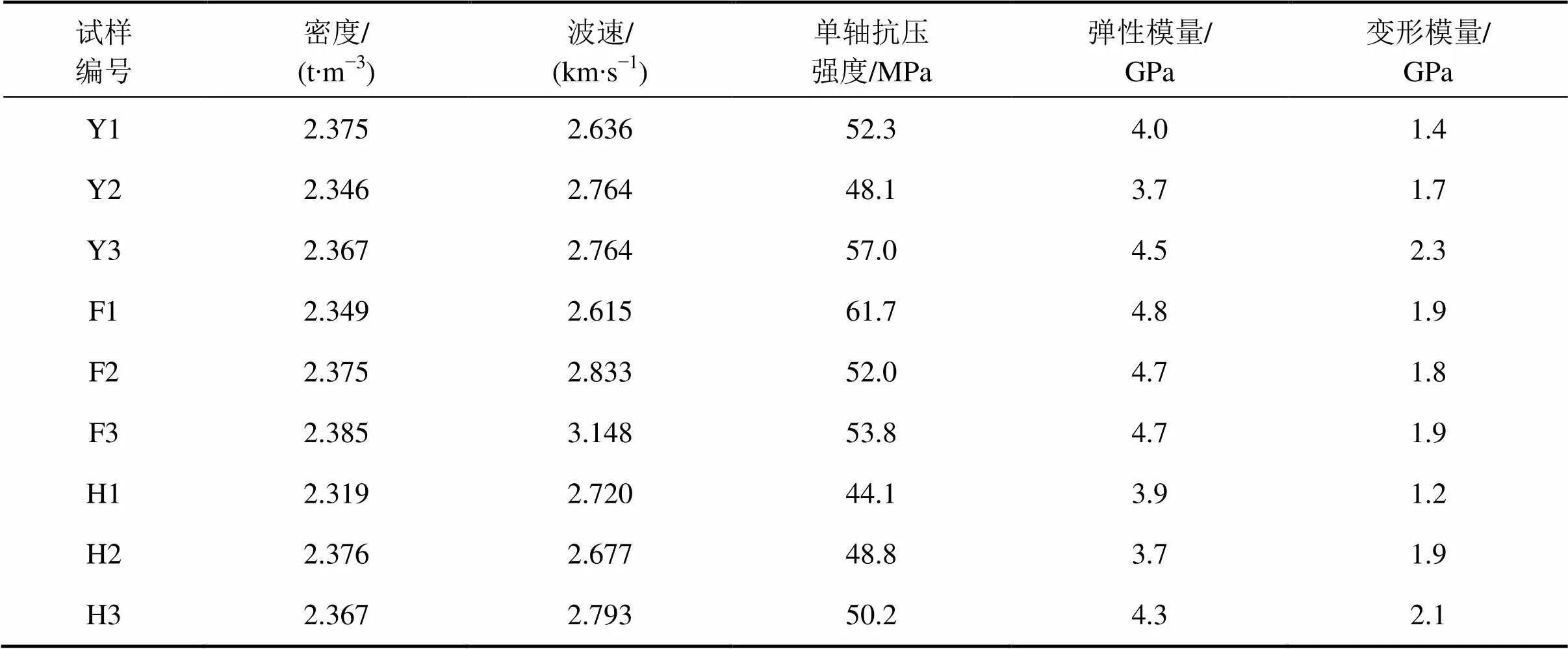
表1 试样单轴压缩试验结果

2 动态冲击试验

2.1 动态测试方法

冲击实验在中南大学冲击动力实验室进行，使用改进后的SHPB设备，如图2所示。SHPB压杆材质为40Cr合金钢，密度为7.810 t/m3，泊松比为0.28，动态弹性模量为250 GPa，纵波速度为5.410 km/s，入射杆长为2.0 m，透射杆长为1.5 m，直径为50.0 mm。子弹为线性变化的“纺锤型”冲头，产生半正弦应力波，由压杆上应变片记录的电压信号转算，数据采集处理系统由超动态应变仪、示波记录仪和计算机组成。

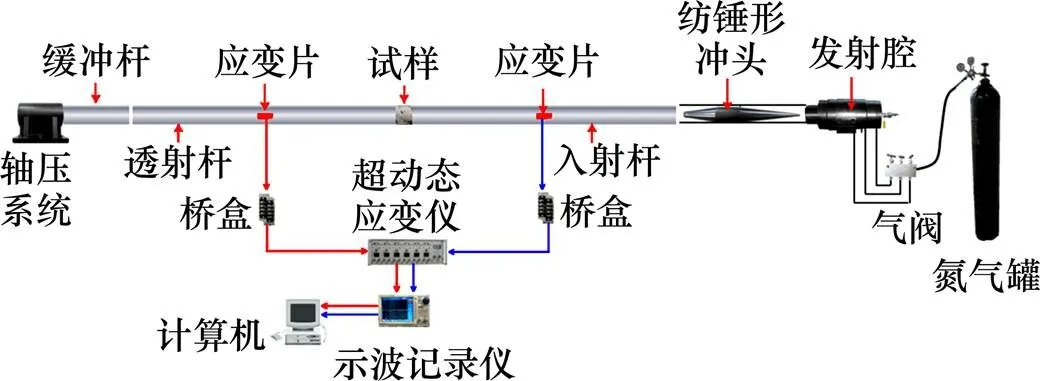
图2 SHPB装置示意图

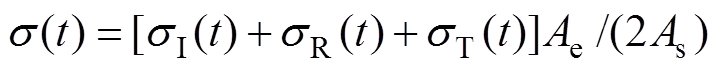
(2)

(3)

应力均匀条件为

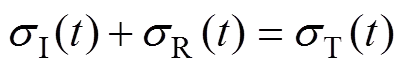
式(1)~(3)可简化为:

(5)

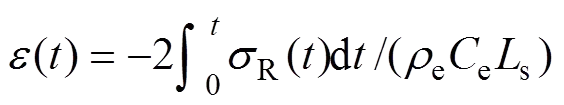
(7)

式中：e为弹性杆横截面面积；s为试样横截面面积；e为弹性杆密度；e为弹性杆波速；s为试样长度；为应力波持续时间；I()R()和T()分别为时刻的入射应力、反射应力和透射应力。式(5)~(7)即基于一维假定及均匀性假定的经典二波法数据处理公式。

2.2 动态应力平衡

SHPB试验结果可靠性保证的基本条件就是试样在破坏前达到应力均匀状态即应力平衡，这样才能有效消除波形弥散和惯性效应。

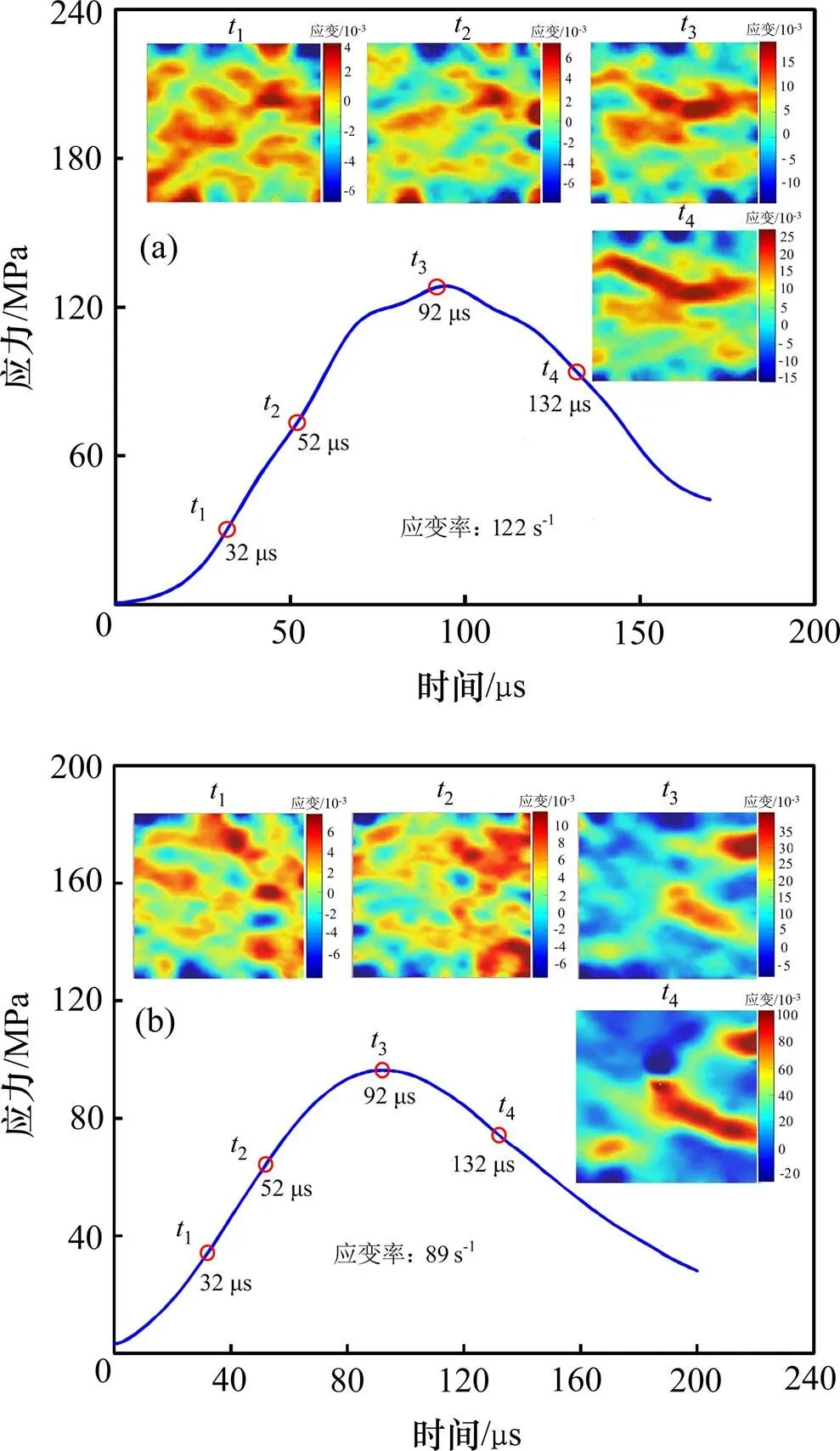
图3所示为试样典型的动态应力平衡曲线。由图3可知：试样在破坏之前，入射应力波和反射应力波之和与透射应力波达到平衡，说明应力波在试样两端多次透射、反射后，试样进入应力均匀状态。当加载到100 μs左右时，应力幅值超过试样的极限强度，试样破坏，透射应力逐渐减少，试样两端开始产生应力差，偏离平衡状态。但破坏前试样两端应力已均匀，破坏后的应力偏差不影响试验结果的可靠性。

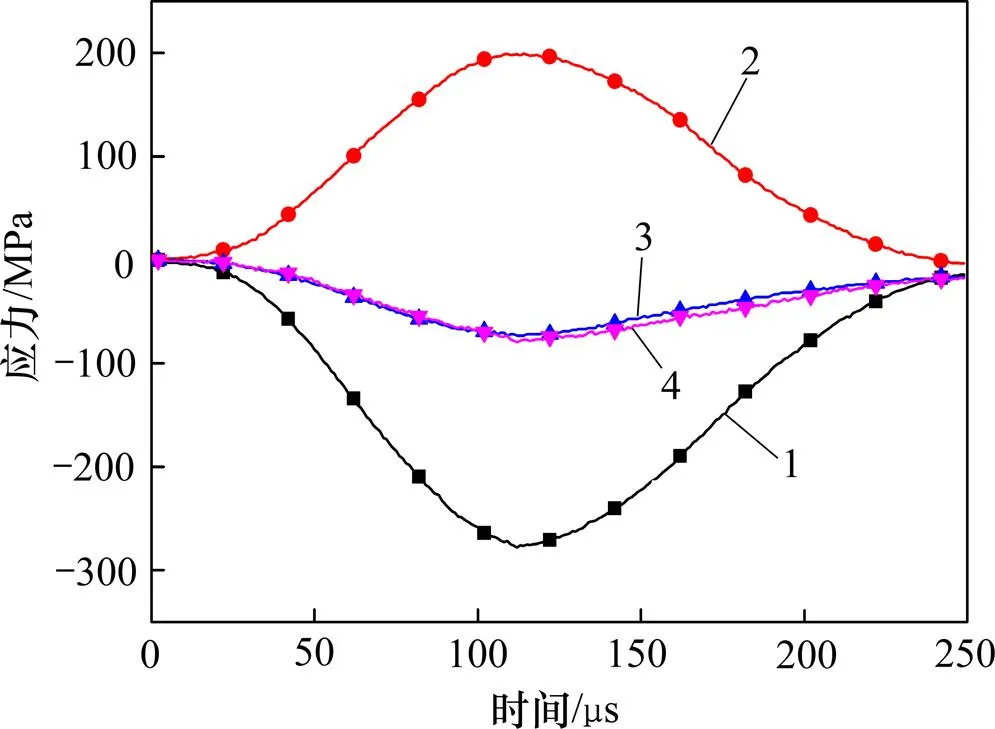
1—入射应力；2—反射应力；3—透射应力；4—入射应力+反射应力

3 动态冲击试验结果

3.1 动态应力−应变曲线

图4所示为冲击载荷下部分砂岩试样的应力−应变全程曲线，表2所示为实验结果。从图4可看出：试样在动载下没有经历压密阶段而直接进入近似弹性阶段。这是因为冲击载荷作用时间很短，试样从开始受力到破坏的时间只有100 μs左右，在这么短的时间内岩石内部的初始微裂隙还来不及闭合，随后试样进入非线性塑性阶段，直到试样发生宏观破坏为止。

当应变率较低时，应力−应变曲线出现回弹，即应变随着应力的减小而逐渐减小，如图4中曲线4所示。这是由于峰后试样并没有完全破坏，仍具有一定的承载能力，岩石内部释放的弹性能量大于加载能量。当应变率较高时，应变随着应力的减少而逐渐增大，试样破碎成块度较小的碎片，与文献[18]中的结论一致。

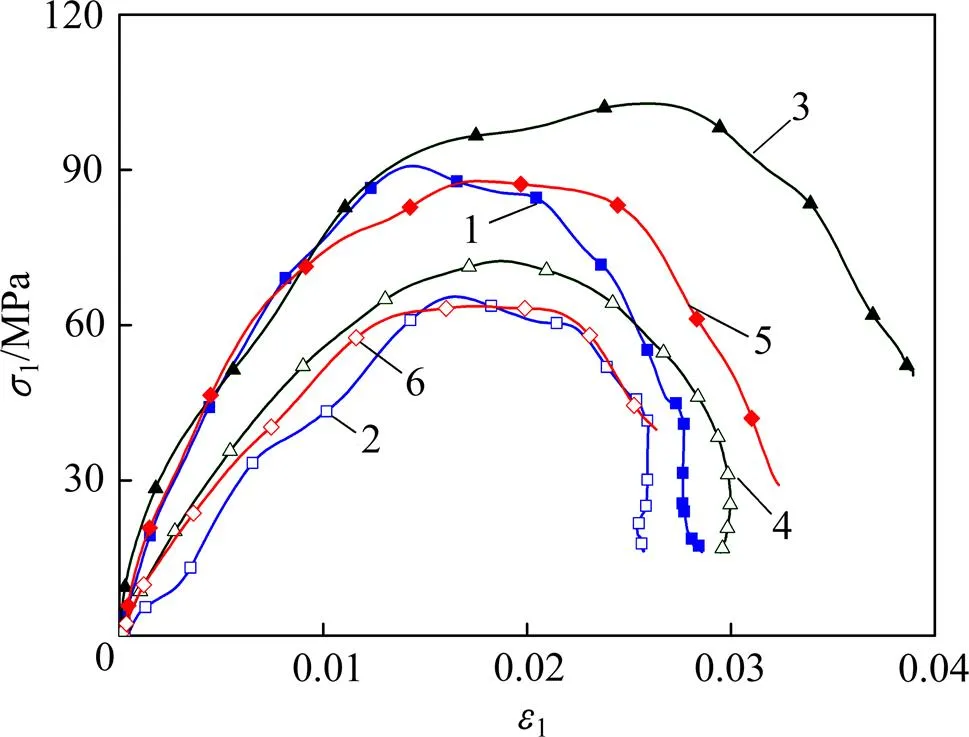
试样：1—Y4；2—Y5；3—F4；4—F5；5—H4；6—H5

表2 砂岩试样动态试验结果

3.2 强度特征

图5所示为试样应变率与动态强度的关系。从图5可看出：除H组1个试样的动态强度与静态强度相当外，其他试样的动态强度均高于静态强度。研究结果表明[19−21]：当应变率小于某值时，材料的动态抗压强度随着应变率的增大并不明显；当应变率大于该值时，动态抗压强度迅速增大，该值可称为临界应变率。由于本文实验应变率主要集中在70 s−1以上，结合静态实验结果，推算3种试样的临界应变率在70 s−1左右。总体来说，在本次试验的应变率范围内，试样的动态强度随着应变率的增大而逐渐增大，具有明显的应变率效应。

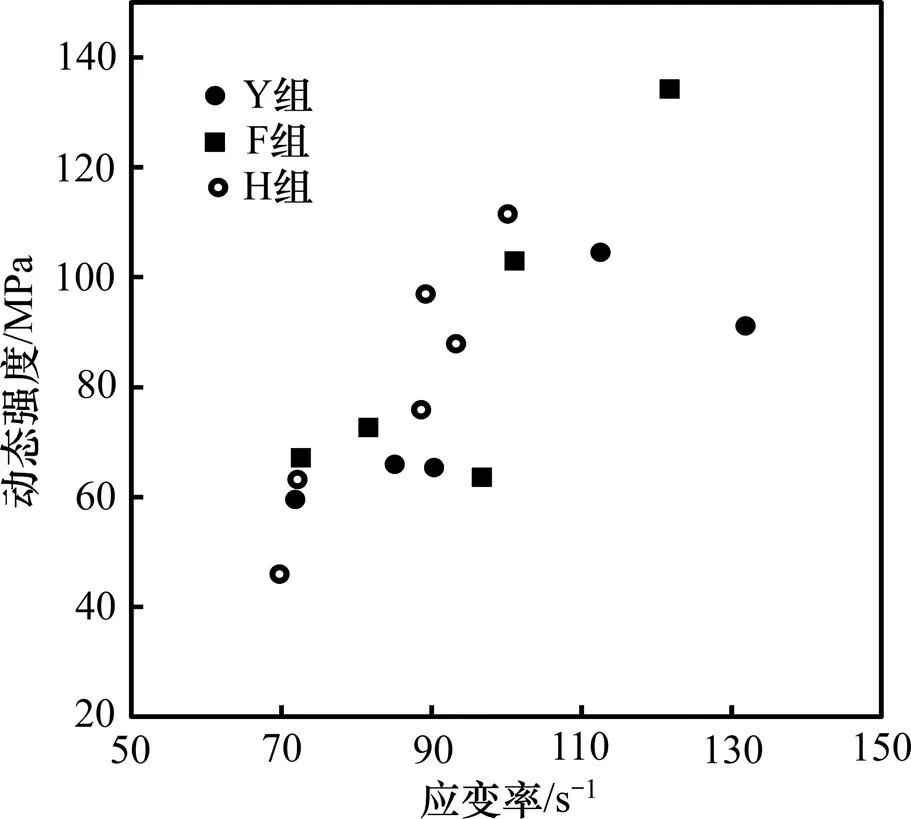
图5 动态抗压强度与应变率的关系

为了分析3种试样动态强度随应变率增长的变化趋势，采用动态强度增长因子即动态抗压强度与静态抗压强度的比值作为冲击荷载下试样抗压强度的增幅指标。动态强度增长因子与应变率的关系如图6所示。从图6可见：厚壁圆筒试样的动态强度增长因子的增速最快，圆柱试样的增速最小，方形试样的增速居中。这表明厚壁圆筒试样比另外2种试样对应变率变化更敏感，这是因为厚壁圆筒试样存在较大自由面，有利于岩石的局部失稳、屈服。

3.3 变形特征

岩样的动态应力−应变曲线直线段很短，没有明显的弹性变形阶段，因此，采用动态变形模量来分析横截面形状对岩石变形的影响。动态变形模量与应变率的关系如图7所示。由图7可知：在本实验的应变率范围内，3种试样的动态变形模量均有随应变率的增大而增大的趋势，但不明显；圆柱试样的变形模量为5.3~10 GPa，平均值为7.6 GPa；方形试样的变形模量为5.7~9.7 GPa，平均值为7.9 GPa；厚壁圆筒试样的变形模量为5.1~10.5 GPa，平均值为7.6 GPa。从表1可知：这3种试样的静态变形模量平均值都在2.0 GPa以下，说明岩石的动态变形模量远远高于静态变形模量。这是因为岩石内部存在许多初始微裂隙，静载下微裂隙闭合，内应力增加较缓，而动载作用时间短，微裂隙来不及闭合，内应力迅速增加。从图7还可知3种试样的动态变形模量随应变率变化的趋势基本一致，表明横截面形状对动态变形模量的影响很小。

图6 动态强度增长因子与应变率的关系

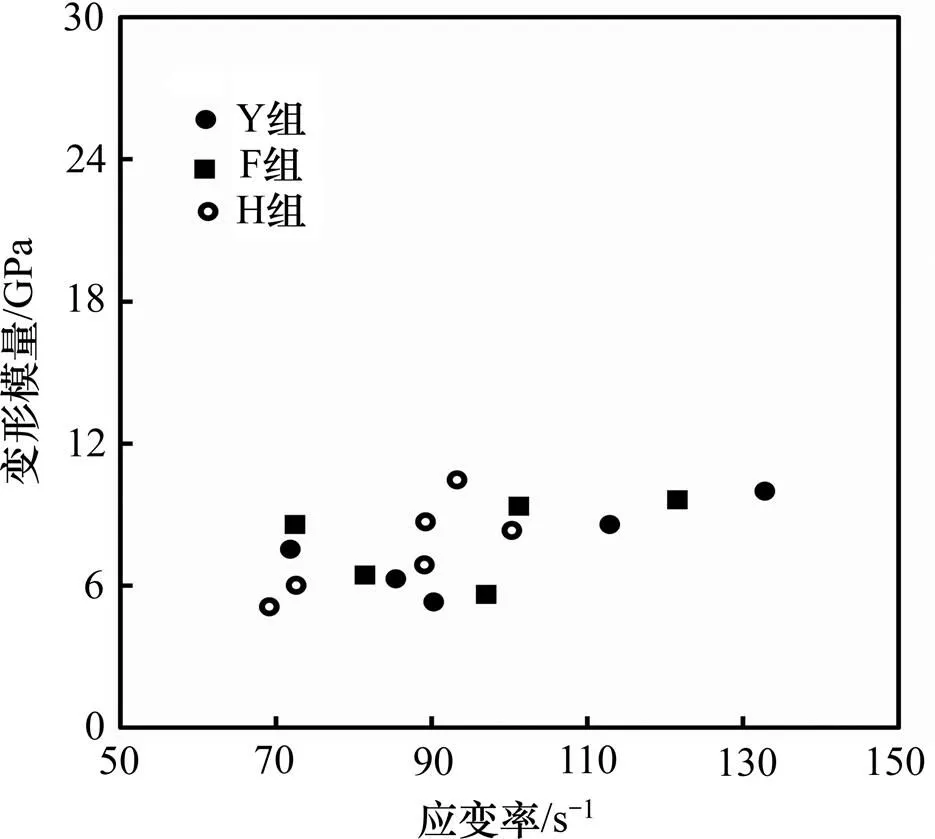
图7 动态变形模量与应变率的关系

图8所示为试样动态峰值应变与应变率的关系。在本实验的应变率范围内，圆柱试样峰值应变的变化范围为0.015~0.018，方形试样为0.016~0.026，厚壁圆筒试样为0.013~0.018。可知方形试样的峰值应变较大，厚壁圆筒试样的峰值应变较小。应变率对峰值应变的影响较离散，峰值应变随应变率变化的趋势不明显。

图8 动态峰值应变与应变率的关系

3.4 全场应变场测量

数字图像相关技术(DIC)作为一种测量变形信息的非接触光学技术已经广泛应用于实验力学领域[22−23]。DIC对光源、被测物体及环境的要求较低，可采用白光源，光路简单，散斑可以是人工散斑，也可以是自然纹理。DIC技术配合高速摄像，可以应用于不同应变率下岩石动态破坏过程的监测。

当前，DIC技术已经应用于岩石材料中[24]。ZHANG等[25]使用DIC技术研究了岩样在不同实验方法下的全场变形特征，CHEN等[26]采用DIC技术研究了3种脆性材料的动态拉伸变形场。然而，利用DIC技术研究半正弦应力波下不同横截面形状岩样变形场的研究成果很少。

为了研究岩石在冲击过程中的变形特征，本文利用数字图像相关技术(DIC)对试样在冲击破坏过程中表面变形场的变化情况进行直观描述。试验时，利用入射杆应变片产生的电压信号，同步触发高速摄像仪与示波器。高速摄像仪帧速设置为50 000 帧/s，即每20 μs拍摄1张，图片分辨率为288像素×256像素，计算区域均为试样表面32 mm×32 mm的方形区域，如图9所示。

利用DIC技术对变形场进行计算时，综合考虑图像分辨率和变形等因素[27]，采用相对较小的图像子区，区域为21像素×21像素，对计算区域进行全场逐点计算。

图10所示为方形试样和厚壁圆筒试样动态冲击过程中的竖向应变场。从图10可发现：32 μs时，方形试样F6在中间位置有明显的拉应力集中区域，中间位置应变明显比其他部位的大，52 μs时达0.007；随着作用动载增加，应变逐渐增大，拉应力集中区域逐渐向试样两端扩展；132 μs时，应变为0.25，在峰值应力时贯穿于整个试样。

图9 试样观测区域散斑图片

(a) F6；(b) H9

而厚壁圆筒试样H9不同，加载过程中拉应力集中区域首先出现在试样入射端，如图10(b)所示。当试样达到峰值强度时，试样右上角的应变最大，为0.025；随着荷载增加，拉应力集中区域逐渐向试样透射端扩展；132 μs时，试样中间位置和右上角应变为0.100，最终形成多个宏观的拉伸破坏面。

冲击荷载下应力波会在岩样中往返多次，产生大量方向不一的裂纹，不同区域的损伤程度不同，所以，用应变电测法来表征全场损伤非常困难。而DIC技术能够直观地描述试样整体变形场的非均匀性和不连续性，便于研究试样变形场的损伤演化过程。

3.5 破坏特征

试样破坏形式如图11所示。从图11可知：在静载下，试样以张拉复合破坏为主，如圆柱试样的劈裂面与轴向加载方向基本平行，不过厚壁圆筒试样内壁并没有出现预先破裂的迹象；在冲击荷载下，试样产生许多方向不一的裂纹，劈裂严重，破碎块度小。

试样：(a) F1；(b) H1；(c) Y1；(d) F7；(e) H9；(f) Y5

实验结果表明：方形试样出现张剪复合破坏，棱角处都会形成明显的剪切面。这可以理解为岩样端部与试验机压头间的摩擦作用使岩样处于三向受压状态，在端面菱角处形成应力集中，有利于裂纹的萌生、扩展、成核和贯通，容易产生剪切滑移。随着深度的增加，摩擦效应逐渐减少，产生剪切滑移且当试样中部的横向拉应力达到抗拉强度时，就会产生剪切和张拉的复合作用破坏形式。

图12所示为试样破碎块度与应变率的关系。从图12可见：随着应变率的增大，3种试样的破碎块度均变小，具有明显的应变率相关性。这是因为冲击入射能大于岩石失稳破坏所需能量，多余的能量促使形成更多的裂纹产生块度更小的岩块，或者转化为岩块弹射动能。

试样(应变率)：(a) Y8(72 s−1)；(b) Y5(90 s−1)；(c) Y4(133 s−1)；(d) F7(73 s−1)；(e) H8(89 s−1)；(f) H6(100 s−1)

4 结论

1) 圆柱试样、厚壁圆筒试样和方形试样的动态强度均随应力率的增大而增大。由于厚壁圆筒试样存在较大自由面，故其比完整试样和方形试样对应变率变化更敏感。

2) 横截面形状对岩石变形模量的影响较小，而对峰值应变的影响较大，峰值应变的应变率效应不明显。

3) 横截面形状和应变率对试样破坏形式的影响较明显，方形试样棱角处均出现明显的剪切面。应变率越大，试样破碎块度越小。

[1] LI X B, LOK T S, ZHAO J, et al. Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress−strain curves for rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(7): 1055−1060.

[2] LI Xibing, ZHOU Zilong, LOK T S, et al. Innovative testing technique of rock subjected to coupled static and dynamic loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 739−748.

[3] 宫凤强, 李夕兵, 刘希灵. 三轴SHPB加载下砂岩力学特性及破坏模式试验研究[J].振动与冲击, 2012, 31(8): 29−32. GONG Fengqiang, LI Xibing, LIU Xiling. Tests for sandstone mechanical properties and failure model under triaxial SHPB loading[J]. Journal of Vibration and Shock, 2012, 31(8): 29−32.

[4] LI Xibing, WU Qiuhong, TAO Ming, et al. Dynamic brazilian splitting test of ring-shaped specimens with different hole diameters[J]. Rock Mechanics and Rock Engineering, 2016, 49(10): 1−9.

[5] 李夕兵, 周子龙, 叶州元, 等.岩石动静组合加载力学特性研究[J]. 岩石力学与工程学报, 2008, 27(7): 1387−1395. LI Xibing, ZHOU Zilong, YE Zhouyuan, et al. Study of rock mechanical characteristics under coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(7): 1387−1395.

[6] 周子龙, 李国楠, 宁树理, 等.侧向扰动下高应力岩石的声发射特性与破坏机制[J]. 岩石力学与工程学报, 2014, 33(8): 1720−1728. ZHOU Zilong, LI Guonan, NING Shuli, et al. Acoustic emission characteristics and failure mechanism of high-stressed rocks under lateral disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(8): 1720−1728.

[7] ZHAO X G, CAI M, WANG J, et al. Strength comparison between cylindrical and prism specimens of Beishan granite under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 76(1): 10−17

[8] 吴秋红, 尤明庆, 苏承东. 各向异性花岗岩的力学参数及相关性[J]. 中南大学学报(自然科学版), 2015, 46(6): 2216−2220. WU Qiuhong, YOU Mingqing, SU Chengdong. Mechanical parameters and relativity of anisotropy granite[J]. Journal of Central South University (Science and Technology), 2015, 46(6): 2216−2220.

[9] 李夕兵. 冲击荷载下岩石能耗及破碎力学性质的研究[D]. 长沙: 中南大学资源与安全工程学院, 1986: 35-40. LI Xibing. A study on the dynamic properties and energy absorption of rocks[D]. Changsha: Central South University. School of Resources and Safety Engineering, 1986: 35-40.

[10] 洪亮, 李夕兵, 马春德, 等.岩石动态强度及其应变率灵敏性的尺寸效应研究[J]. 岩石力学与工程学报, 2008, 27(3): 526−533. HONG Liang, LI Xibing, MA Chunde, et al. Study on size effect of rock dynamic strength and strain rate sensitivity[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 526−533.

[11] OLSSON W A. The compressive strength of tuff as a function of strain rate from 10−6to 103/s[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1991, 28(1): 115−118.

[12] FREW D J, FORRESTAL M J, CHEN W. A split Hopkinson pressure bar technique to determine compressive stress-strain data for rock materials[J]. Experimental Mechanics, 2001, 41(1): 40−46.

[13] ZOU Chunjiang, WONG L N Y. Size and geometry effects on the mechanical properties of carrara marble under dynamic loadings[J]. Rock Mechanics & Rock Engineering, 2016, 49(5): 1695−1708.

[14] LINDHOLM U S, YEAKLEY L M. High strain-rate testing: tension and compression[J]. Experimental Mechanics, 1968, 8(1): 1−9.

[15] AHMAD I R, SHU D W. Effect of specimen diameter in compression at high strain rates[J]. Journal of Engineering Mechanics, 2011, 137(3): 169−174.

[16] GUNASEKERA J S, HAVRANEK J, LITTLEJOHN M H. The effect of specimen size on stress-strain behavior in compression[J]. Journal of Engineering Materials & Technology, 1982, 104(4): 274−279.

[17] SEN O, TEKALUR S A, MAITY P. On the use of non-cylindrical specimens in a split-Hopkinson pressure bar[J]. Journal of Strain Analysis for Engineering Design, 2011, 46(46): 866−878.

[18] 宫凤强, 李夕兵, 刘希灵, 等.一维动静组合加载下砂岩动力学特性的试验研究[J]. 岩石力学与工程学报, 2010, 29(10): 2076−2085. GONG Fengqiang, LI Xibing, LIU Xiling. Experimental study of dynamic characteristics of sandstone under one-dimensional coupled static and dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2076−2085.

[19] ZHANG Q B, ZHAO J.A review of dynamic experimental techniques and mechanical behaviour of rock materials[J]. Rock Mechanics & Rock Engineering, 2014, 47(4): 1411−1478.

[20] 宫凤强. 动静组合加载下岩石力学特性和动态强度准则的试验研究[D]. 长沙: 中南大学资源与安全工程学院, 2010: 96−100. GONG Fengqiang. Experimental study of rock mechanical properties under coupled static-dynamic loads and dynamic strength criterion[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2010: 96−100.

[21] 洪亮. 冲击荷载下岩石强度及破碎能耗特征的尺寸效应研究[D]. 长沙: 中南大学资源与安全工程学院, 2008: 78−82. HONG Liang. Size effect on strength and energy dissipation in fracture of rock under impact loads[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2008: 78−82.

[22] HILD F, ROUX S. Digital image correlation: from displacement measurement to identification of elastic properties: a review[J]. Strain, 2006, 42(2): 69−80.

[23] PAN B. Recent progress in digital image correlation[J]. Experimental Mechanics, 2011, 51(7): 1223−1235.

[24] SONG Haipeng, ZHANG Hao, KANG Yilan, et al. Damage evolution study of sandstone by cyclic uniaxial test and digital image correlation[J]. Tectonophysics, 2013, 608(6): 1343−1348.

[25] ZHANG Q B, ZHAO J. Determination of mechanical properties and full-field strain measurements of rock material under dynamic loads[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 60(8): 423−439.

[26] CHEN J J, GUO B Q, LIU H B, et al. Dynamic Brazilian test of brittle materials using the split Hopkinson pressure bar and digital image correlation[J]. Strain, 2015, 50(6): 563−570.

[27] YU Hai, GUO Rongxin, XIA Haiting, et al. Application of the mean intensity of the second derivative in evaluating the speckle patterns in digital image correlation[J]. Optics & Lasers in Engineering, 2014, 60(178): 32−37.

(编辑 陈灿华)

Dynamic properties of sandstones with different shapes

XIE Xiaofeng, TAO Ming, WU Qiuhong, WANG Zewei, SHANG Xueyi, LIU Kai

(School of Resources and Safety Engineering, Central South University, Changsha410083, China)

To evaluate the influence of cross-section shape on the dynamic mechanical properties of rock, impact tests on cylinder, prism and thick-walled hollow cylinder sandstone specimens were conducted using modified split Hopkinson pressure(SHPB) system. The results show that the dynamic compressive strength of three kinds of specimens increases with the increases of the strain rate. The strain rate effect of the thick-walled specimens increases more sharply than that of the other two specimens since the thick-walled specimens have larger free faces. Cross-section shape has small influence on rock deformation modulus but large influence on peak strain, and the strain rate effect of peak strain is not obvious. Cross-section shape and strain rate influence the failure mode significantly. Shear failure faces appear at the corners of the prism specimens, and the rock fragment size decreases with the increase of the strain rate.

rock mechanics; split Hopkinson pressure (SHPB); dynamic properties; shape effect; strain rate; strength

10.11817/j.issn.1672-7207.2017.09.024

TU458

A

1672−7207(2017)09−2441−08

2016−10−27；

2016−12−22

国家自然科学基金资助项目(51404303)；中南大学中央高校基本科研业务费专项资金资助项目(2015zzts084) (Project(51404303) supported by the National Natural Science Foundation of China; Project(2015zzts084) supported by the Fundamental Research Funds for the Central Universities of Central South University)

陶明，博士，副教授，从事岩石力学与采矿工程研究；E-mail: mingtao@csu.edu.cn