颗粒实际形状在PFC数值研究中的模拟方法

林呈祥，凌道盛



颗粒实际形状在PFC数值研究中的模拟方法

林呈祥1, 2，凌道盛1, 2

(1. 浙江大学建筑工程学院，浙江杭州，310058;2. 浙江大学软弱土与环境土工教育部重点实验室，浙江杭州，310058)

针对颗粒实际形状在PFC 数值研究中的模拟，总结4 种主要模拟方法。在简要介绍PFC 计算原理及其基本命令“Clump”的基础上，对每种模拟方法的主要步骤进行概述，并对比分析每种模拟方法的优缺点。研究结果表明：4 种模拟方法都需要先获得颗粒的表面轮廓，然后在其表面轮廓的基础上通过一定的方式把基本颗粒单元粘结在一起从而实现对颗粒实际形状的模拟，其中以“Clump”命令应用为主。构造颗粒实际形状所用的基本颗粒单元个数越多，数值模拟的精度就越高，但相应的计算时间也就越长，选择合适的颗粒形状模拟方法是平衡模拟精度和计算效率的关键。

颗粒材料；颗粒形状；离散元法；PFC数值研究

CUNDALL[1]在20世纪70年代初基于分子动力学原理提出离散元法(distinct element method，DEM)，其基本思想是把非连续介质看作一系列离散单元的集合，单元间存在相对运动，但不一定满足位移连续和变形协调条件，通过时步迭代求解各单元的运动方程，继而得到非连续体的整体运动形态[2]。颗粒流软件(particle flow code，PFC)[3−4]是美国ITASCA公司基于离散元法研发的程序，在计算过程中交替应用牛顿第二运动定律于颗粒单元，接触力−位移法则于颗粒接触上，实现循环计算，并能对颗粒的排列状态、接触力链、位移场等实时记录并提取。PFC数值研究具有计算速度快、费用低、操作性好、重复性强等优点，已被逐渐应用到土体渗透破坏、液化变形、剪切带形成等非连续变形问题的研究中[5]。PFC数值研究是离散元法中最为常用的方法，在不同领域的课题研究中都得到了广泛应用，尤其是在模拟研究颗粒材料时具有独特的优势。颗粒形状对颗粒材料的宏观性质如密实度、剪切特性，压缩特性及颗粒破碎特性等都着重要的影响[6]。而PFC中颗粒的默认形状为简单的圆形(2D)或球体(3D)，这和形状千差万别的实际颗粒存在巨大的差别，限制了PFC数值研究的进一步应用。为取得可靠的计算结果，提高数值模拟精度，需考虑颗粒实际形状这一影响因素进行PFC数值研究。在考虑颗粒形状的早期PFC数值研究中，椭圆(球)形、多边形(体)、超曲面等不规则形状常被用来对比模拟研究颗粒形状对力学性质的影响[7−14]；JIANG等[15]则在颗粒的接触模型中引入抗转动作用考虑颗粒实际形状的影响。砂土颗粒的形状量化及模型构造是PFC数值研究的难点[16−17]，随着计算机技术的迅猛发展以及扫描摄像技术的不断改善，对颗粒实际形状的模拟已成为可能，也成为PFC数值研究的一大热点[18−23]；而在国内，考虑颗粒实际形状影响因素的PFC数值研究报道较少。为此，本文作者在介绍PFC计算原理及“Clump”命令的基础上，总结国外相关文献中对颗粒实际形状进行PFC模拟的主要方法，并对它们的优缺点进行讨论与总结，以便为下一阶段考虑颗粒实际形状影响因素的PFC数值研究提供参考。

1 PFC计算原理

在PFC程序的每个计算时步(time-step)开始前，基于颗粒、墙体的位置确定接触，然后应用力−位移法则更新每个接触的接触力；再对每个颗粒运用牛顿第二定律，根据作用于颗粒上的接触力、体积力引起的合力、合力矩更新每个颗粒的速度和位置；交替重复这2个步骤，实现循环计算直至结束[3−4]。

图1 颗粒接触简化模型

1.1 力−位移法则及运动定律

颗粒接触简化模型如图1所示。PFC中颗粒间的接触力F可分解为法向接触力和切向接触力：

法向接触力随颗粒间重叠量的增大而线性增大，计算公式为

切向接触力以增量的形式来计算得到，如下式所示：

；(4)

颗粒的运动情况由颗粒上一点的线速度与角速度来描述，分别由作用于其上的合力和合力矩来决定：

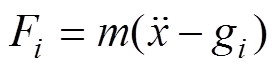
(6)

1.2 Clump命令

在PFC软件中，可以通过粘结基本颗粒形成一个“颗粒簇(cluster)”，也可以应用“Clump”命令让基本颗粒通过一定的排列方式粘结成为1个刚形体，来模拟不同形状的实际颗粒。由个基本颗粒通过“Clump”命令粘结而成的颗粒簇的质量和质心位置可由下式计算得出：

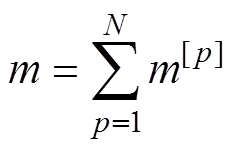
(8)

其中：上标[]表示各个单独颗粒；颗粒簇可看成是一种特殊的颗粒单元体，其运动情况仍可按式(5)和式(6)来描述。

2 对颗粒实际形状的模拟

MATSUSHIMA等[18−19]提出一种动态优化的离散元算法来模拟颗粒的实际形状，以2D模拟为例，其基本思路为：在颗粒的平面区域内随机生成一定数量直径不同的基本圆，在一般情况下，基本圆的半径比被模拟颗粒的小；在颗粒表面布置一组离散点，并假设离散点对基本圆有一种“虚力(virtual force)”，其作用方向在基本圆圆心和离散点的连线上并指向离散点，其大小正比例于离散点和基本圆间的距离，如图2(a)和2(b)所示；且每个离散点只对距离最近的基本圆有“虚力”作用，如图2(c)所示；在“虚力”作用下，基本圆产生平移、膨胀(或收缩)等运动，并在阻尼作用下趋于平衡；最后所有的基本圆通过“Clump”命令粘结成一个整体，即是对颗粒实际形状的模拟。

(a) 基本圆部分在颗粒形状轮廓外的受力情况；(b) 基本圆完全在颗粒形状轮廓里的受力情况；(c) 颗粒形状轮廓上的离散点只对最近的基本圆有作用力

当只有1个基本圆时，模拟结果只有1个，且与基本圆的起始位置和大小无关；而当有多个基本圆时，模拟结果并不唯一，而是会受到基本圆初始配置(位置和大小)的影响。因此，MATSUSHIMA等[18−19]提出了一种误差指数来评判模拟结果的精确程度：

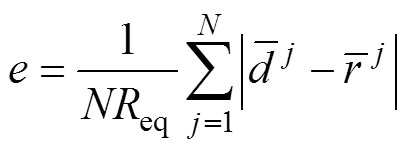
其中：为颗粒表面的离散点个数；eq为被模拟颗粒同面积圆的半径；为第个离散点和最近基本圆圆心的距离；为基本圆的半径。误差指数最小的即为颗粒形状的最优模拟结果。图3所示为采用10个基本圆对砂土颗粒形状的PFC 2D模拟图。

(a) 颗粒初始图像；(b) 十单元颗粒模型图

图3 对颗粒形状的PFC 2D模拟[18]

Fig. 3 PFC 2D simulation of particle shapes[18]

WANG等[20]在对路面颗粒材料进行DEM模拟研究时提出了一种对不规则形状颗粒的模拟方法，如图4所示。模拟过程大致可分为3步：在颗粒的数字图像上, 沿像素区间用一系列同半径的基本圆单元来填充；对相邻区域内的基本圆尽可能地用1个半径更大的圆来替代，以此来减少圆的总数；把所有圆粘结成一个整体。利用此方法既可以对平面形状，也可以对空间立体形状进行模拟，如图5和图6所示；FERELLEC等[22]利用此方法对一空间正八面体进行了模拟，结果如图7所示。

PRICE等[21]提出了一种以颗粒表面为导向(surface-driven)的3D模拟方法，先通过照相机对颗粒的各个方向进行拍照得到颗粒轮廓，然后通过空间黏聚合成可视立体外壳，并在颗粒外壳表面布置网格节点，最后依据网格节点来进行颗粒形状的模拟，如图8所示。

图4 平面不规则形状颗粒模拟过程[20]

(a) 平面正三角形原图；(b) 模拟图

(a) 原不规则形状颗粒；(b) 模拟图

图7 对正八面体的模拟[22]

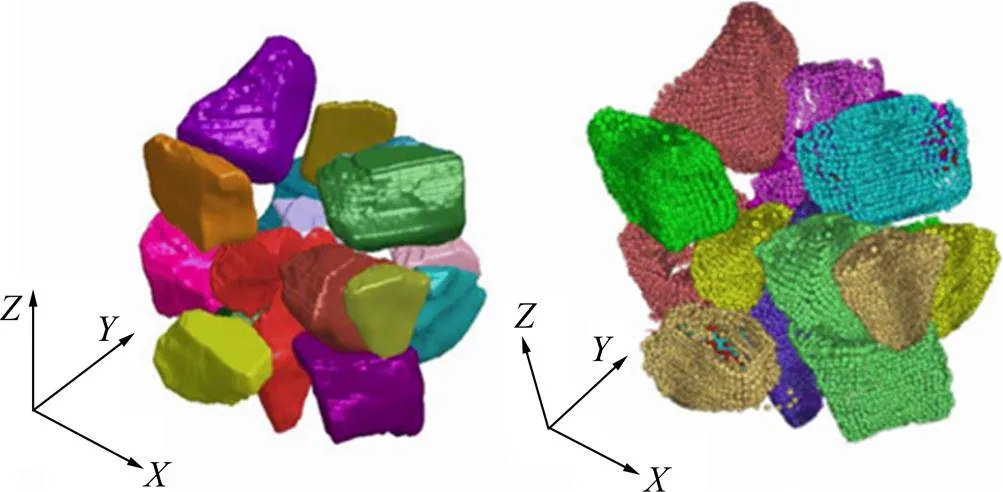
该方法包括“初始化”和“最优化”2个主要过程，初始化过程为：根据空间四点(非共面)只要满足其中任意3点都不在同一直线上就能确定1个球体的原则，在颗粒表面的网格节点上随机选取4点来确定1个基本球单元；对所有的网格节点都循环1遍直到颗粒的空间区域几乎被基本球单元所充满为止，如图8(a)所示；把颗粒表面的网格节点和与其距离最近的基本球单元对应起来，如图8(b)所示，左边的基本球单元对应实心黑点的这些表面节点；通过移动/涨缩基本球单元使其与这些对应颗粒表面节点的平均相对距离最小，从而达到最优配置，如图8(c)所示。图9所示为应用该方法对一些典型形状颗粒的3D模拟图。从图9可以看出，此方法能较好地模拟具有凸面形状特性的颗粒。

(a) 用基本球单元来填充颗粒的空间区域；(b) 把颗粒表面的网格节点和与其距离最近的基本球单元对应起来；(c) 移动/涨缩基本球单元达到最优配置

FERELLEC等[22−23]提出了一种相对更加简单快捷的方法来实现对颗粒实际形状的模拟，具体步骤为：通过镭射扫描或者立体摄影得到颗粒的表面离散网格，均匀布置网格节点；在节点上产生基本圆，并沿该节点的内法线方向在颗粒区域内尽可能膨胀，直至接触到颗粒的另一表面节点为止，如图10所示。对其余节点依次重复以上第2步，使得所有的节点都有相对应的基本圆；用“Clump”命令把所有基本圆粘结成一个整体，即可实现对颗粒形状的模拟。

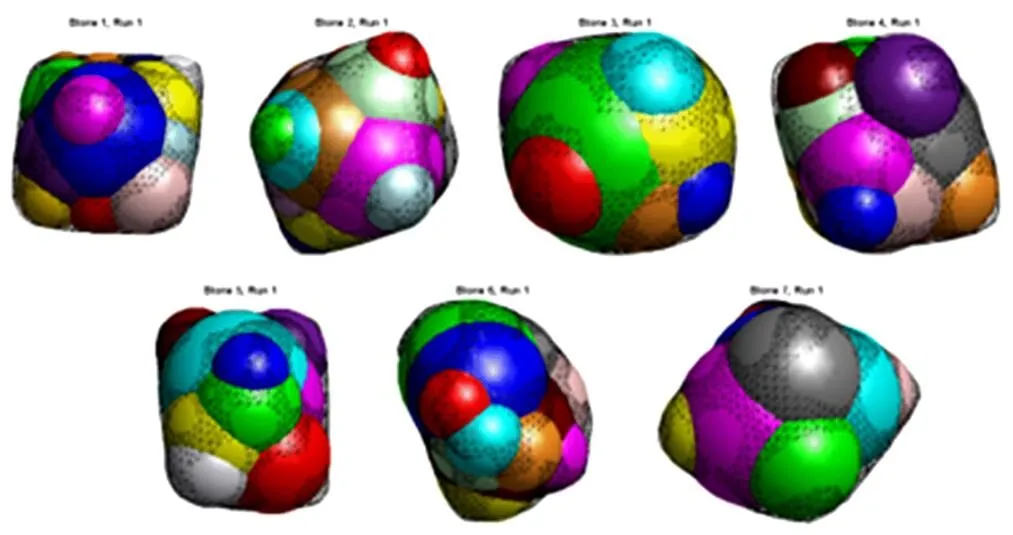
图9 典型颗粒的3D模拟图[21]

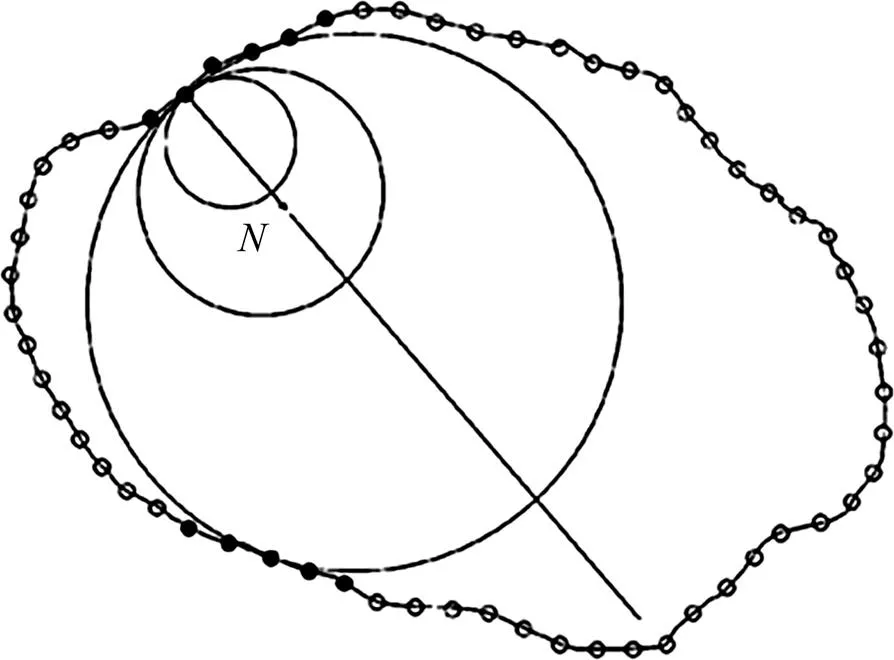
图10 沿节点内法线方向膨胀基本圆示意图[22]

颗粒表面的网格节点分布越密，最后产生的基本圆数量越多，颗粒形状的模拟精度越高，但最后模拟计算的时间也越长。实际上，并不一定要对所有的表面节点都要产生1个基本圆，如果表面节点和已有的基本圆距离很近(如图10中的实心黑点)，那么对它们就没有必要再产生新的基本圆；因此，可以先设定1个距离参数min，当节点和已有基本圆的距离小于min时，就不产生新的基本圆，这样就可以大大减少最后基本圆的总数量，从而节约计算时间。也可以设定最大节点百分比max来限制基本圆的数量，当随机选定的节点数达到一定百分比时就中断程序。另一个控制基本圆数量的方法就是删除半径过小的基本圆，当新产生的基本圆半径小于预设的临界值min时，将被自动删除。图11所示为当min=1.8 mm，max=1%，min=3 mm时对1个实际颗粒的PFC数值模拟图结果。

为了减少最后基本圆的总数量，以此来缩短计算时间提高计算效率，设置min，max和min这3个参数，但是，减少基本圆数量会相应地降低颗粒形状的模拟精度，如何平衡模拟精度和计算效率就需要根据具体的应用课题来决定。对于一些不需要考虑精确颗粒形状的定性研究来说，可以适当减少基本圆的数量来提高计算效率；而对于颗粒形状是重要研究因素的课题来说，就需要增加基本圆数量保证对颗粒实际形状的模拟精度。

(a) 颗粒立体图；(b) PFC模拟图

3 讨论

作为离散元法中重要的模拟手段，PFC数值方法在求解大变形、非线性等复杂问题中具有独特优势，尤其在研究颗粒材料细观力学方面表现尤为突出。如何采用一种高效快捷的方法对颗粒实际形状进行模拟是今后PFC数值研究的重点任务之一。文中列举了4种主要模拟方法，每种模拟方法都有各自的优缺点，具体如下。

1) MATSUSHIMA等[18−19]提出的方法是一个动态的模拟过程，减少了很多手动对基本颗粒圆的调整作业，但是其初始大小的选择以及位置的分布对模拟的结果有很大影响，需要不断地尝试才能找到合适的初始配置；初始基本圆的个数会直接影响到模拟的精度，但考虑到计算时间，并不是基本圆的个数越多越好，需要找到最优的基本圆个数。虚拟力参数的选取及基本圆的变形模量亦没有参考标准，难以推广应用。

2) WANG 等[20]提出的方法可直接利用颗粒数字图像的像素区间快速生成基本圆单元，也就是说，数字图像的像素精度决定了初始基本圆的半径；数字图像像素越高，基本圆的半径越小，颗粒实际形状的模拟精度越高。但是，该方法模拟所用的圆单元数量一般相对庞大，对一个普通形状颗粒的模拟至少也需要几千个圆单元，从而导致后续程序的计算时间较长，模拟效率相对较低。在模拟带棱角、勾角等复杂颗粒形状时，所得结果和实际结果相差较大，并且模拟的颗粒表面都较为粗糙。

3) PRICE等[21]提出的方法在确定基本球单元时需要对颗粒表面的每个网格节点进行循环定位计算，且要求初始选取的4个网格节点最好是位于同一侧区域，后续的距离计算及优化过程也较繁琐；当有多个不同颗粒形状时，整个模拟过程非常耗时，并且对于一些表面具有棱角、勾角等凹面结构的颗粒则很难模拟，因此，该方法不具有代表性。

4) FERELLEC等[22−23]提出的方法相对方便快捷，原则上能对任何不规则形状的颗粒都能模拟，并且可根据研究课题对形状模拟精度的需要适当选择网格节点的密度及调整min，max，min这3个参数的数值；但在模拟不同尺寸的颗粒时，3个参数需要重新选择，应用性不强。因此，需要在这3个参数的基础上提出相对应的量纲一的参数来模拟不同尺寸量级的颗粒，扩大其应用范围。

由于非圆形颗粒的引入，颗粒之间的接触关系判断变得复杂，也降低了PFC程序的计算速度，在分析颗粒数量较多的试样时需耗费大量的时间，从而会使得数值研究效率下降。一般来说，构造颗粒实际形状所用的基本颗粒单元个数越多，数值模拟的精度越高，但相应的计算时间也就越长；因此，如何选择合适的形状模拟方法以及合理的基本颗粒单元个数是平衡模拟精度和计算效率的关键。

4 结论

1) 颗粒空间表面轮廓的获取是对颗粒形状进行模拟的前提条件，文中所列的4种主要模拟方法需要先对颗粒进行扫描或者拍照等操作获得其空间表面轮廓，然后在其表面轮廓的基础上通过一定的方式把基本颗粒单元粘结在一起从而实现对颗粒实际形状的模拟，其中以“Clump”命令应用为主，让基本颗粒单元相互重叠成一个刚形体。

2) 非圆形颗粒的引入使颗粒之间的接触关系判断变得复杂，降低了数值模拟的研究效率。一般来说，构造颗粒实际形状所用的基本颗粒单元个数越多，数值模拟的精度就越高，但相应的计算时间也就越长，选择合适的颗粒形状模拟方法是平衡模拟精度和计算效率的关键。

[1] CUNDALL P A. A computer model for simulating progressive large scale movements in blocky rock systems[C]// MULLER L, ed. Proceeding of the Symposium of the International Society for Rock Mechanics. Rotterdam: Balkama A A, 1971: 8−12.

[2] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Geo-technique, 1979, 29((1): 47−65.

[3] Itasca Consulting Group, Inc. The manuals of particle flow code in 2 dimension. Version 3.0[M]. Minneapolis: Mill Place, 2002.

[4] Itasca Consulting Group, Inc. The manuals of particle flow code in 3 dimension, Version 4.0[M]. Minneapolis: Mill Place, 2008.

[5] ZHU H P, ZHOU Z Y, YANG R Y, et al. Discrete particle simulation of particulate systems: a review of major applications and findings[J]. Chemical Engineering Science, 2008, 63(23): 5728−5770.

[6] 孔亮, 彭仁. 颗粒形状对类砂土力学性质影响的颗粒流模拟[J]. 岩石力学与工程学报, 2011, 30(10): 2112−2119. KONG Liang, PENG Ren. Particle flow simulation of influence of particle shape on mechanical properties of quasi-sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2112−2119.

[7] ROTHENBURG L. Micromechanical features of granular assemblies with planar elliptical particles[J]. Geo-technique, 1992, 42(1): 79−95.

[8] LIN X, NG T T. A three-dimensional discrete element model using arrays of ellipsoids[J]. Geo-technique, 1997, 47(2): 319−329.

[9] CHANG Y L, CHU B L, LIN S S. Numerical simulation of gravel deposits using multi-circle granule model[J]. Journal of the Chinese Institute of Engineering, 2003, 26(5): 681−694.

[10] ROTHENBURG L, BETHURST R J. Numerical simulation of idealized granular assemblies with plane elliptical particles[J]. Computers and Geotechnics, 1991, 11(4): 315−329.

[11] TING J M, MEACHUM L R, ROWELL J D. Effect of particle shape on the strength and deformation mechanisms of ellipse-shaped granular assemblages[J]. Engineering Computations, 1995, 12(2): 99−108.

[12] JENSEN R, EDIL T, BOSSCHER P, et al. Effect of particle shape on interface behaviour of DEM-simulated granular materials[J]. International Journal of Geo-mechanics, 2001, 1(1): 1−19.

[13] VU-QUOC L, ZHANG X, WALTON O R. 3D discrete-element method for dry granular flows of ellipsoid particles[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 187(3): 483−528.

[14] LIZCANO A A, ALONSO M F, HERRMANN H J. Biaxial test simulations using a packing of polygonal particles[J]. International Journal for Numerical and Analytical Method in Geomechanics, 2008, 32(1): 143−160.

[15] JIANG M J, YU H S, HARRIS D. A novel discrete model granular material incorporating rolling resistance[J]. Computers and Geotechnics, 2005, 32(4): 340−357.

[16] 刘清秉, 项伟, BUDHU M, 等. 砂土颗粒形状量化及其对力学指标的影响分析[J]. 岩土力学, 2011, 32(增刊1): 190−197. LIU Qingbing, XIANG Wei, BUDHU M, et al. Study of particle shape quantification and effect on mechanical property of sand [J]. Rock and Soil Mechanics, 2011, 32(S1): 190−197.

[17] 张程林, 周小文. 砂土颗粒三维形状模拟离散元算法研究[J]. 岩土工程学报, 2015, 37(增刊1): 115−119. ZHANG Chenglin, ZHOU Xiaowen. Algorithm for modeling three-dimensional shape of sand based on discrete element method[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S1): 115−119.

[18] MATSUSHIMA T, SAOMOTO H. Discrete element modeling for irregularly-shaped sand grains[C]// Proc NUMGE 2002: Numerical Methods in Geotechnical Engineering. Paris: LCPC, 2002: 239−246.

[19] KATAGIRI J, MATSUSHIMA T, YAMADA Y. Simple shear simulation of 3D irregularly-shaped particles by image-based DEM[J]. Granular Matter, 2010, 12(5): 491−497.

[20] WANG L, PARK J, FU Y. Representation of real particles for DEM simulation using X-ray tomography[J]. Construction and Building Materials, 2007, 21(2): 338−346.

[21] PRICE M, MURARIU V, MORRISON G. Sphere clump generation and trajectory comparison for real particles[C]// Proceedings of the Fourth International Conference on Discrete Element Methods (DEM). Brisbane, 2007: 105−113.

[22] FERELLEC J F, MCDOWELL G R. A simple method to create complex particle shapes for DEM[J]. Geomechanics and Geoengineering: An International Journal, 2008, 3(3): 211−216.

[23] FERELLEC J F, MCDOWELL G R. A method to model realistic particle shape and inertia in DEM[J]. Granular Matter, 2010, 12(5): 459−467.

(编辑 赵俊)

Simulation of real particle shape in PFC numerical analysis

LIN Chengxiang1, 2, LING Daosheng1, 2

(1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China;2. Key Laboratory of Soft Soils and Geo-environmental Engineering of Ministry of Education,Zhejiang University, Hangzhou 310058, China)

For the simulation of real particle shape in PFC numerical analysis, four main methods were summarized. The calculation theory of PFC, as well as its basic command “Clump”, was briefly introduced before the main steps of each method were outlined. Afterwards, the advantages and disadvantages of all the four methods were compared and discussed. The results show that in all the four methods, the surface profile of particles needs to be obtained at first. On the basis of surface profile, basic elements are bonded together through a certain way to simulate the real particle shape, among which the “Clump” command is mostly used. The higher the number of the basic elements used, the higher the simulation accuracy is; meanwhile, the longer time it takes to calculate. Taking an appropriate method to simulate the real particle shape plays decisive role in balancing the simulation precision and the computational efficiency.

granular material; particle shape; discrete element method; PFC numerical analysis

10.11817/j.issn.1672-7207.2017.09.022

TU443

A

1672−7207(2017)09−2425−07

2016−11−04；

2017−02−25

国家自然科学基金资助项目(51278451)；浙江省自然科学基金资助项目(LZ12E09001) (Project(51278451) supported by the National Natural Science Foundation of China; Project(LZ12E09001) supported by the Natural Science Foundation of Zhejiang Province)

凌道盛，博士，教授，从事月壤力学、土动力学、计算力学及数值模拟研究；E-mail: dsling@zju.edu.cn