基于岩体蠕变试验的Burgers改进模型

唐佳，彭振斌，何忠明



基于岩体蠕变试验的Burgers改进模型

唐佳1, 2，彭振斌1，何忠明3

(1. 中南大学地球科学与信息物理学院，湖南长沙，410083；2. 中国电建集团中南勘测设计研究院有限公司地质工程处，湖南长沙，410007；3. 长沙理工大学交通运输工程学院，湖南长沙，410076)

以湖北潘口水电站进水口边坡岩体为研究对象进行室内蠕变试验，得到岩样的应力−应变曲线和相应的力学参数；对本构模型进行分析，提出改进方法。在Mohr−Coulomb准则(M−C准则)基础上引入新的M−C塑性元件，提出Burgers改进蠕变模型。研究结果表明：白云石英片岩和绿泥钠长片岩具有明显的蠕变特性，在不同级别的荷载力加载下，加载应力与应变以比例方式增大；这2种岩体材料同时具有黏塑、瞬塑、瞬弹和黏弹特性，这4种特性随着应力增大也呈增强趋势；这2种岩体材料在饱和状态下蠕变现象更明显；Burgers改进蠕变模型能够对黏弹塑性偏量特征及弹塑性体积进行模拟。

岩体；蠕变特性；M−C塑性元件；改进模型

岩体应变随着时间的推移会逐渐呈现出明显的蠕变性。岩体常常具备非常强的时间效应，岩体初期应力在总体上较大，之后，应力随着时间增加而不断增大，随后进入应力调整期，此时，增加速度不断降低，最后进入一个持续时间较长的平衡期[1−4]。徐平等[5]认为岩石是一种蠕变体，必须考虑边坡岩体在长期荷载作用下的稳定性。李连崇等[6]认为，由于岩体的流变特性，岩体强度参数随时间的推移而逐渐衰减，致使边坡稳定程度降低。刘光廷等[7]指出，与干燥状态相比，软岩泡水后除了瞬时变形模量大幅度降低外，流变也很显著。佘成学等[8]提出流变瞬时强度概念，建立了岩石和节理面的非线性黏塑性流变破坏模型的一般形式。王明芳等[9]采用五元件黏弹性剪切流变模型对花岗岩流变的黏弹性流变曲线进行拟合，得到模型的流变参数。刘东燕[10]等通过分级加载蠕变试验得出在相同围压下，有无孔隙水压岩石蠕变都可能存在1个相同的应力强度阀值，当应力强度超过该阀值时便会出现加速蠕变破坏。杨振伟等[11]基于颗粒流理论和Burgers模型，采用颗粒离散元方法进行岩石二维离散元虚拟单轴蠕变试验，研究颗粒粒径、摩擦因数、颗粒法向与切向刚度比对流变特性模拟值的影响。然而，这些研究主要针对自然状态下岩石的蠕变特性，而对于水化环境下岩体力学性能的时间效应研究较少。为此，本文作者以湖北省潘口水电站进水口边坡岩体为研究对象，通过室内蠕变试验得到岩样的应 力−应变曲线，通过数据处理方法得到相应的力学参数，并对本构模型进行分析，提出改进方法，以便为岩体边坡稳定性的时间效应研究提供参考。

1 岩体蠕变试验

1.1 试验设备及岩样制备

岩体蠕变试验设备为RYL−600微机控制岩石剪切流变仪，配以德国DOLI全数字伺服控制系统(EDC)。通过试验可以检测出岩石的抗压强度、剪切强度，实时得出岩石单轴压缩的应力−应变全过程 曲线。

试验选取湖北省潘口水电站进水口边坡白云石英片岩和绿泥钠长片岩2种岩体，现场进行岩样切割、钻芯、打磨，试验参数见表1。为了研究库水对岩体力学性质的影响，将试样分别置于自然状态下和浸泡水溶液中。试样在水溶液中浸泡20 d以上。当试样的质量保持稳定不变时，认为其达到饱和。

表1 试样参数

1.2 试验流程

根据试验设备条件、技术要求及有关因素，本次蠕变试验采用分级增量加载。将试样置于加载台中间，下降加载头至接触试样(预加荷载为300~500 N)，调整底板直至试样与加载装置充分接触为止。加载初始荷载10 kN，分级荷载增量为40 kN，以0.3 kN/s的加载速率加载至预定荷载，将载荷保持稳定。在此过程中，计算机适时记录数据并保存为相应文件。持续观测试验数据，在24 h内，当岩样的轴向变形量小于0.001 mm时，认为其蠕变变形达到稳定状态。循环进行下一级蠕变试验，直至试样最终破坏为止。

1.3 试验结果分析

白云石英片岩在自然状态下的蠕变试验曲线见图2。从图2可见：在荷载作用瞬间，应变与时间的关系呈线性特征；随着时间增加，岩样进入蠕变阶段；当加载应力为5.0 MPa、时间超过25 h时，蠕变加载曲线呈现出较明显的波动现象，岩体处于细微缺陷压密阶段；当加载应力为25.0 MPa时，岩体内部结构受到压密，岩体微裂隙被闭合，绝大部分微缺陷被压密；当加载应力为45.0 MPa时，3 h内岩样变形基本完成；当加载应力增加至65.0 MPa时，岩样内部结构受到破坏，但未产生明显的损伤弱化，蠕变曲线仍较稳定。

(a) 单载加载；(b) 分级增量单调加载；(c) 分级增量循环加卸载

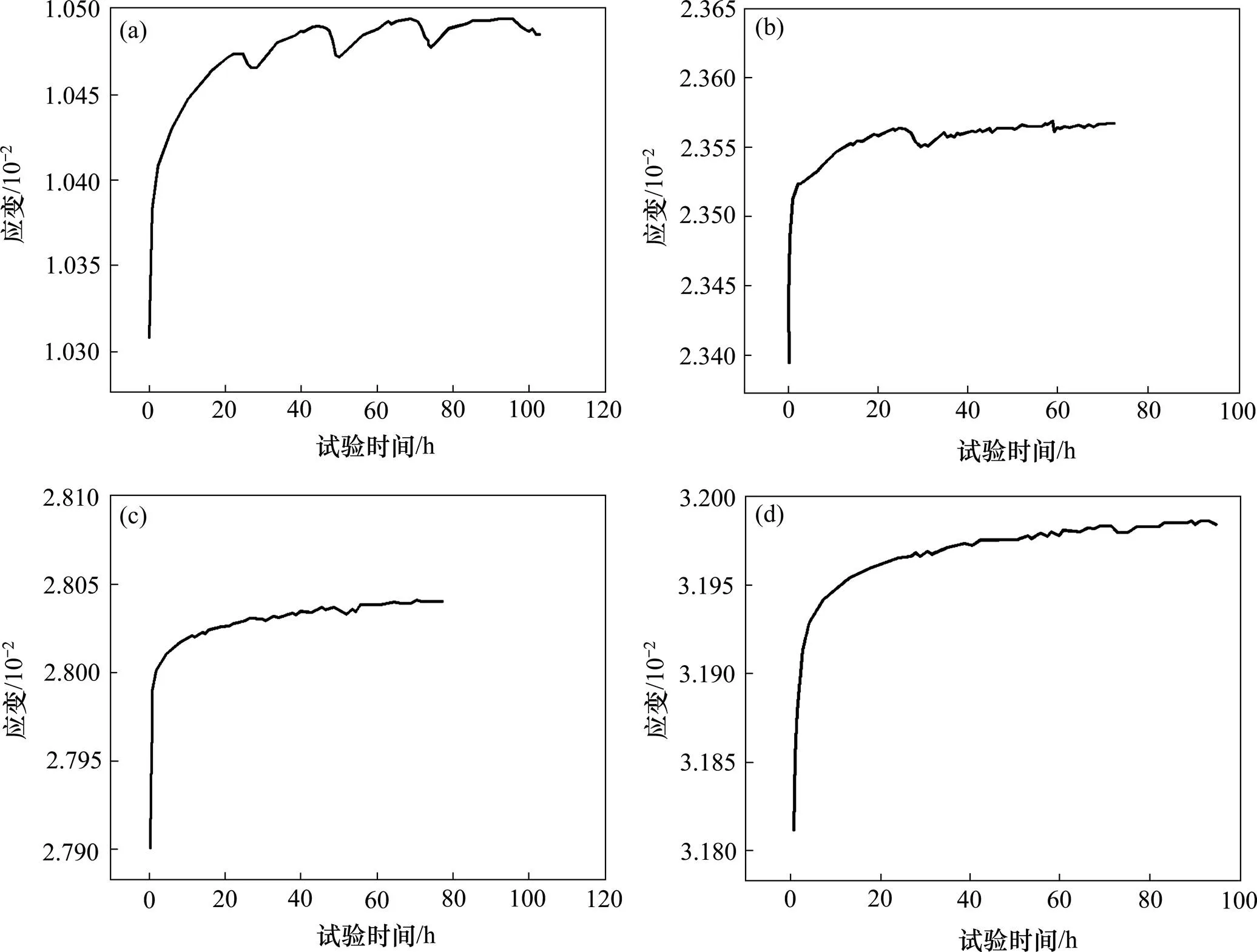
试验压力/MPa：(a) 5.0；(b) 25.0；(c) 45.0；(d) 65.0

白云石英片岩在饱水状态下的蠕变曲线见图3。从图3可见：在饱水状态下，岩样的强度较自然状态下有所降低；当加载应力为5.0 MPa时，曲线呈波动递增，与自然状态下的曲线类似；在加载应力为25.0 MPa时，试件很快进入稳定蠕变阶段，蠕变应变增量较小，经过65 h后轴向应变为1.5×10−2；当加载到45.0 MPa时，岩样出现较明显的加速蠕变现象，在外部压力和水共同作用下，原始缺陷发展成宏观裂纹，在很短时间内试件发生破坏。

绿泥钠长片岩在自然状态下的蠕变曲线见图4。从图4可见：在第1级加载应力5.0 MPa作用下，内部原生缺陷不断调整，114 h后对应轴向应变为0.7×10−2；当加载应力为25.0 MPa时，试样存在显著衰减蠕变，保持荷载达到70 h后其轴向应变较稳定；当达到加载应力45.0 MPa时，试样达到稳态蠕变， 90 h后相应的轴向应变达1.7×10−2；当达到第4级加载应力65.0 MPa时，试样加速蠕变，发生破坏。

绿泥钠长片岩在饱水状态下的蠕变曲线见图5。由图5可知：在加载应力5.0 MPa作用下，43 h后轴向应变稳定于0.98×10−2；在加载应力为25.0 MPa时，试件进入到稳定蠕变阶段，53 h后轴向应变稳定于1.77×10−2；当加载应力达到45.0 MPa时，岩样出现显著的加速蠕变特征，但该现象持续时间不长，约0.25 h后试样即遭破坏；当加载应力为65.0 MPa时，岩样出现快速蠕变现象，仅维持不到0.5 h就发生了破坏。

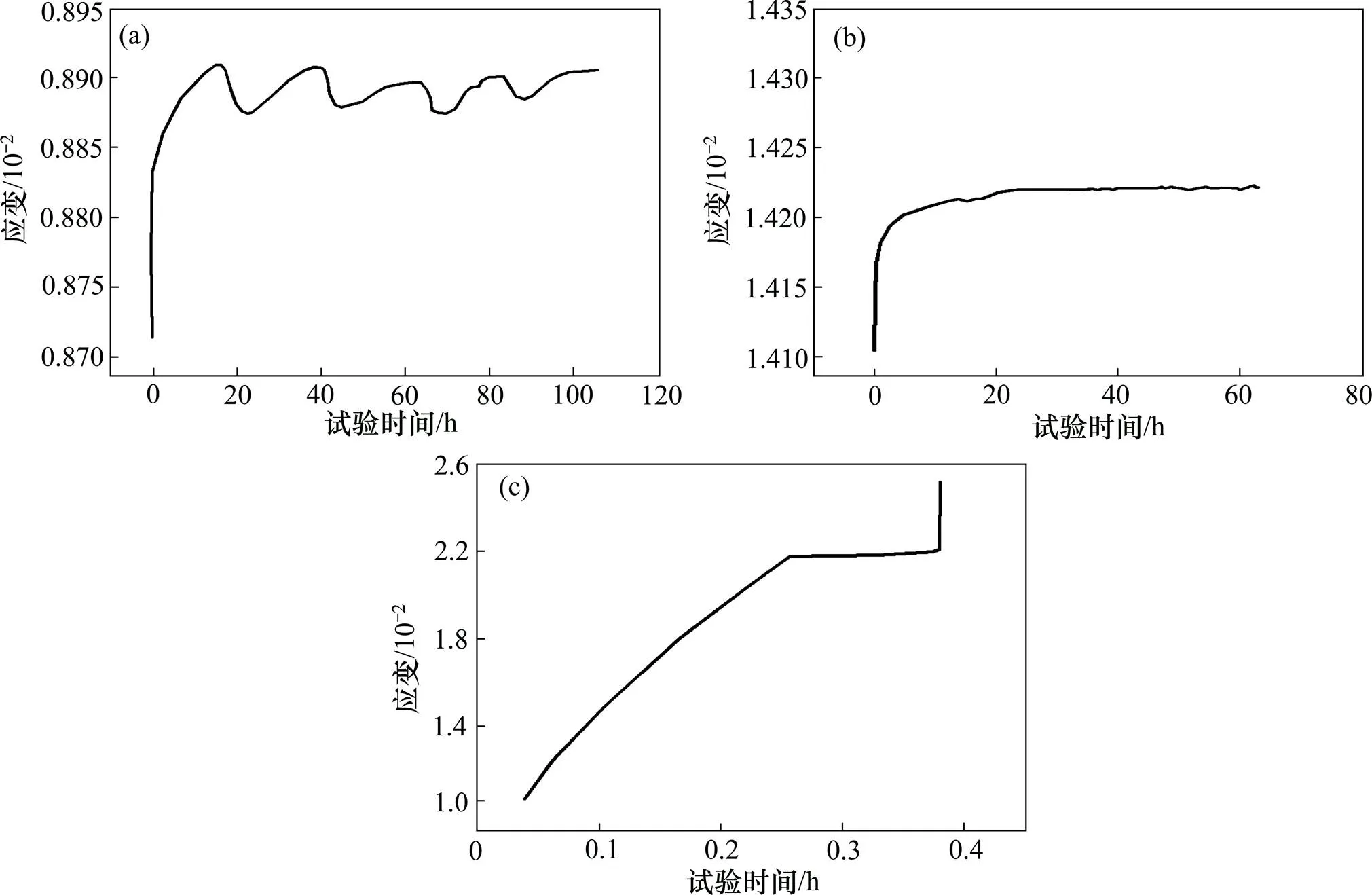
试验压力/MPa：(a) 5.0；(b) 25.0；(c) 45.0

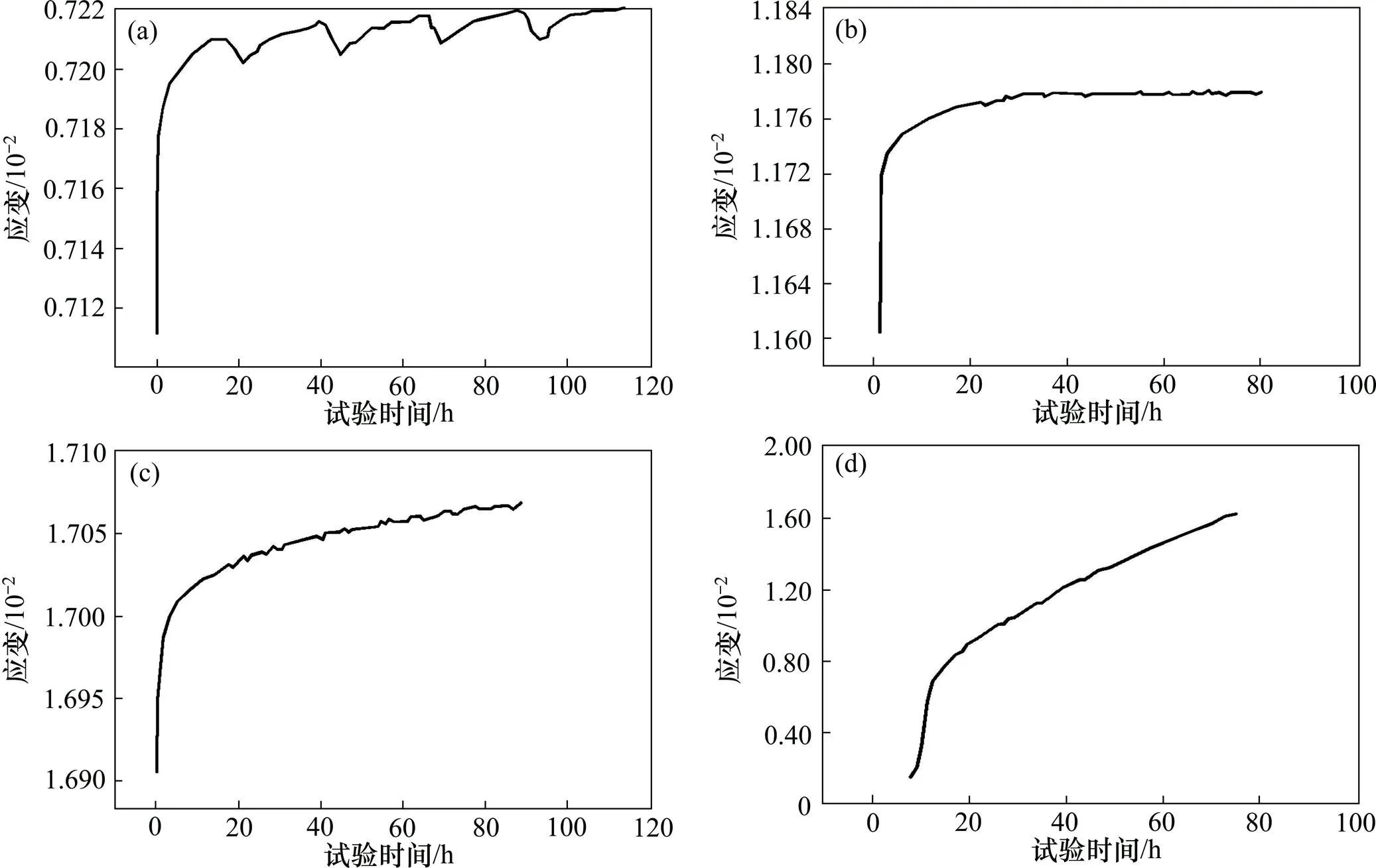
试验压力/MPa：(a) 5.0；(b) 25.0；(c) 45.0；(d) 65.0

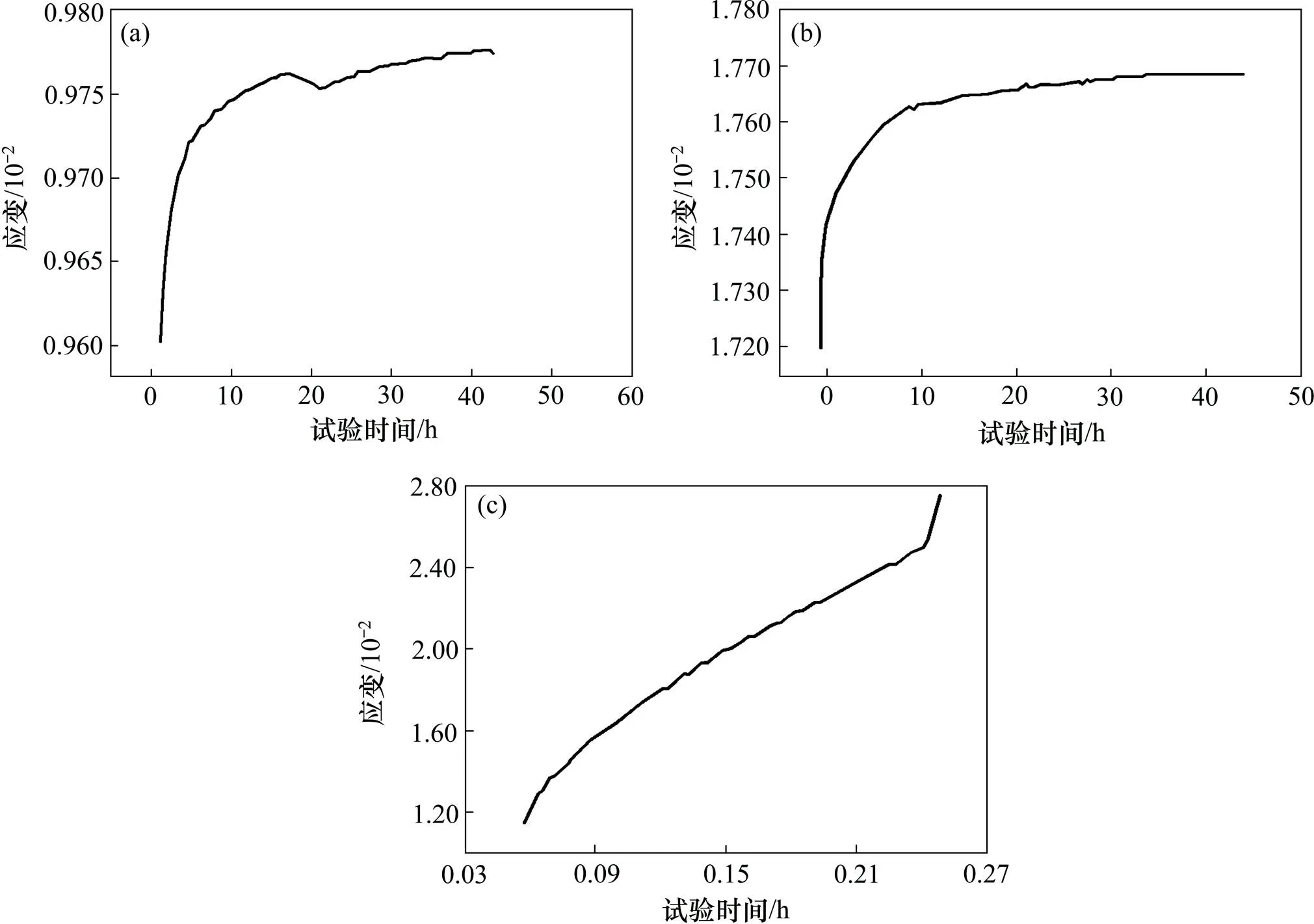
试验压力/MPa：(a) 5.0；(b) 25.0；(c) 45.0

2 岩体蠕变应力应变特征

2.1 岩体蠕变模型

通过分析不同岩样饱水与自然状态不同加载应力下蠕变试验曲线可知：

1) 在每一级荷载或位移施加瞬间，试件均产生一定的瞬时变形或应力，且应力与应变呈线性关系，说明在蠕变应力应变模型中存在弹性元件。

2) 应变随荷载增大而增大，然后越来越稳定。但当施加荷载小于岩体的长期强度时，蠕变速率慢慢减小并渐渐接近零；相反地，蠕变速率维持稳定不变，岩体材料具有黏性，相关黏性元件也存在于蠕变模型中。

3) 岩体同时产生了弹性应变和残余变形，同时拥有随时间可以恢复的黏弹性应变和不可恢复的黏塑性的应变，塑性元件应包含在流体模型中。

4) 在应力水平较低时，岩体材料表现为典型的弹性特征；而当应力水平较高时，典型的黏弹塑性特征在试样上开始出现。

2.2 非线性黏弹塑性蠕变模型

2.2.1 非线性黏塑性体

引用文献[12]中的NVPB(非线性黏性体)模型(图6)来反映岩体蠕变过程中加速蠕变特性。该模型在恒应力0作用下蠕变方程为

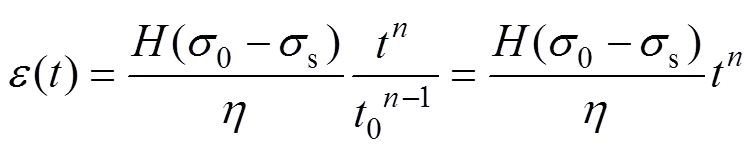
(2)

非线性黏塑性蠕变模型曲线如图7所示。从图7可见：当=1时，NVPB模型中的应变与时间呈线性关系，该蠕变方程在西原模型中，是塑性体和黏性体的并联组合；当＜1时，随着时间增长，应变速率(曲线斜率)不断减小，表现为衰减蠕变现象；当＞1时，随着时间增长，应变速率(曲线斜率)则逐渐增大，呈现出其非线性加速蠕变特性。当蠕变指数取值不同时，NVPB(非线性黏塑性体)模型在描述岩体的蠕变全过程曲线上非常有效。

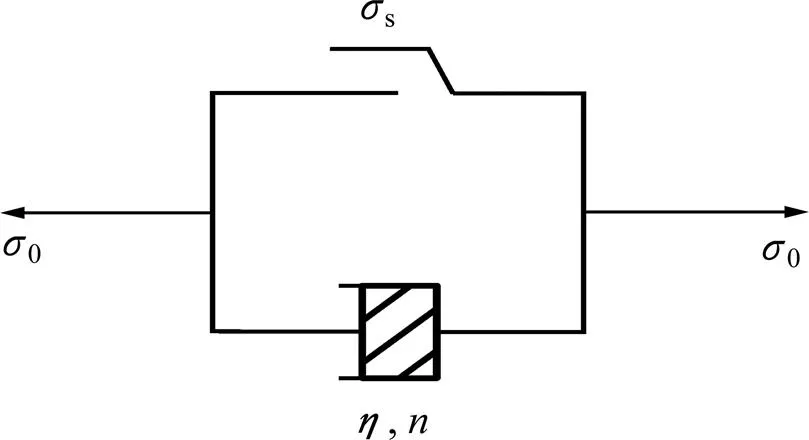
图6 非线性黏塑性模型

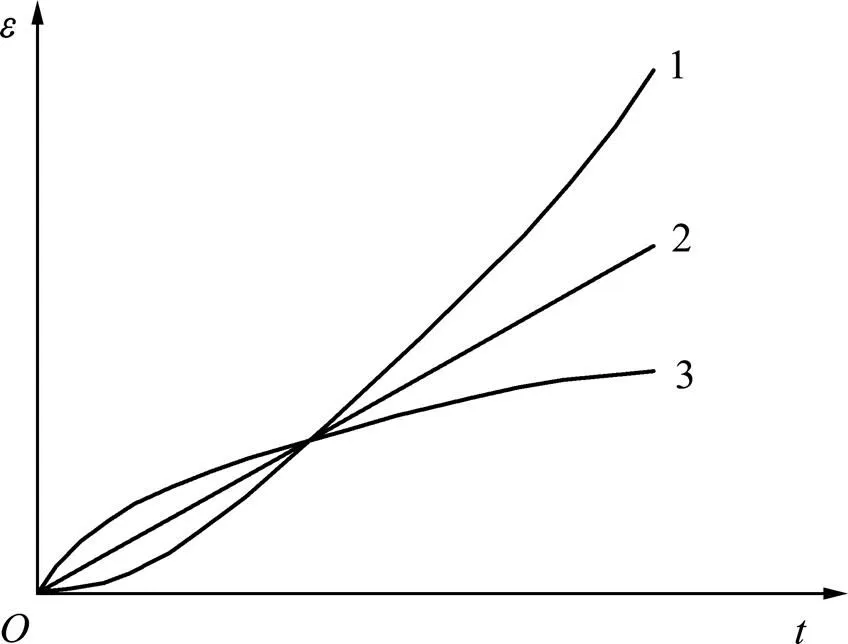
1—n＞1；2—n=1；3—n＜1。

2.2.2 非线性黏弹塑性蠕变模型

潘口水电站进水口边坡岩体具有黏、弹、塑三性共存的特点，并且在高应力作用下呈现出明显的非线性加速蠕变现象，同时具有应力阀值。当应力水平高于应力阀值时，岩体发生蠕变变形。为能较好地描述岩体的非线性加速蠕变特性且充分反映岩体的应力阀值，提出一种新的的岩体非线性黏弹塑性蠕变模型，如图8所示。图8中：和分别为模型的总应力和总应变；1，2，3和4分别为第1~4部分对应的应力；1，2，3和4分别为第1~4部分对应的应变；1，2和3分别为第1~3级材料的弹性参数；1，2和3分别为第1~3级材料的黏性参数；为蠕变指数；s1为岩体的应力阀值；s2为岩体的屈服应力或长期强度。NVPB模型能反映岩体的非线性加速蠕变性质，塑性元件s1为应力阀值，用以保证岩体蠕变变形随时间而增大。

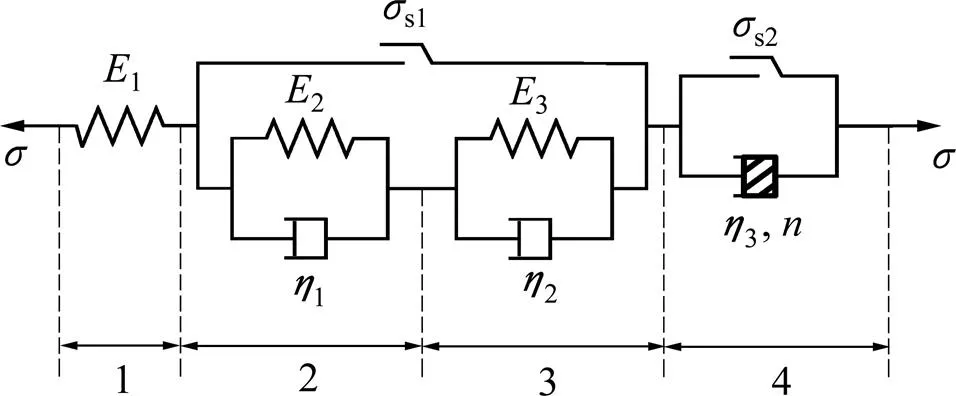
图8 岩体非线性黏弹塑性蠕变模型

1) 当应力0＜＜s1＜s2时，仅第1部分参与作用，此时处于弹性阶段，蠕变模型为虎克模型，相应的本构方程为

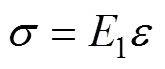
若施加应力，且0≤s1，应力0保持不变，则此时模型不发生蠕变，应变恒等于01。

若施加一应变0且10≤s1，使应变保持不变，则岩体无松弛特征，应力恒等于10。

2) 当应力0＜s1＜＜s2时，第1，2和3部分参与作用，此时，为考虑应力阀值的线性黏弹性蠕变模型，相应的状态方程为

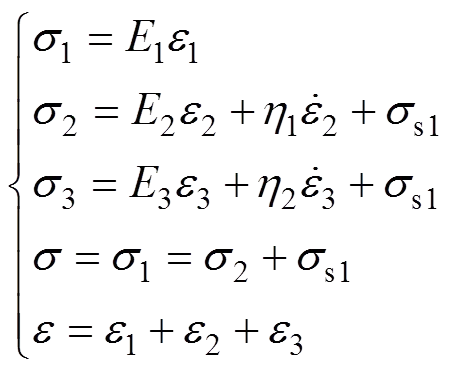
本构方程为

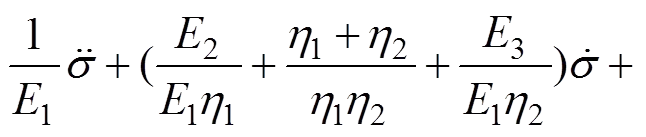
(5)

若施加一应力0，且s1＜≤s2，应力0保持不变，据式(4)和(5)并考虑初始条件进行Laplace变换及Laplace逆变换，可得蠕变方程：

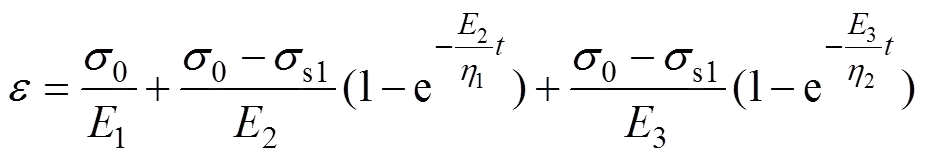
此时，在该模型中发生瞬时弹性和蠕变变形，且当时间增加时，蠕变速率不断减小，最终变形量趋于定值。

若施加一应变0，且0＜s1＜10＜s2，则使应变保持不变，则据式(4)和(5)并考虑初始条件，通过Laplace变换及Laplace逆变换，可得松弛方程：

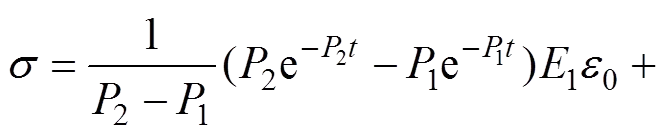
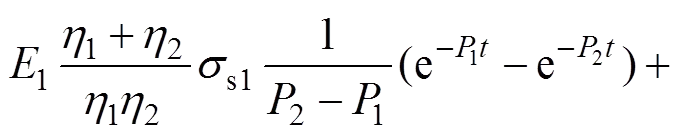
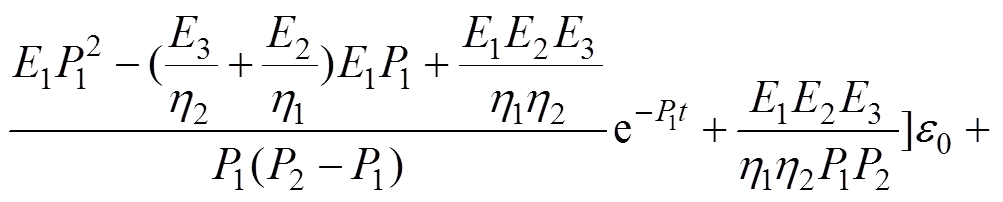
(7)

其中：

；

；

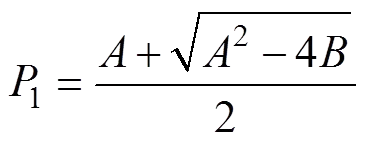
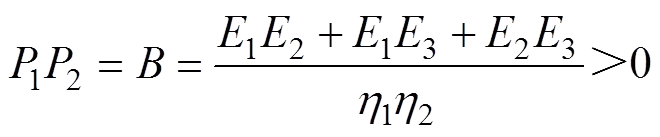
3) 当应力0＜s1＜s2＜时，第1~4部分均产生作用，因此，对应的状态方程为

(8)

此时，本构方程为

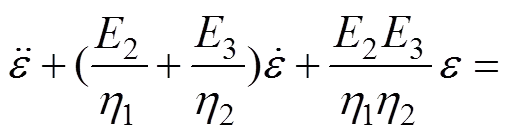
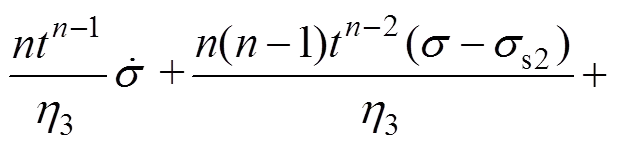
(9)

若施加一应力0，且0＞s2，应力0保持不变，根据式(9)并考虑初始条件，进行Laplace变换及Laplace逆变换，可得蠕变方程：

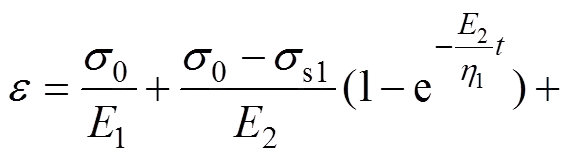
(10)

在＝1时，蠕变模型不能反映加速蠕变，只能反映初始蠕变和稳定蠕变；当＞1时，定二阶导数小于0的蠕变模型用于描述岩体初始蠕变阶段，大于0的蠕变模型用于描述稳定蠕变阶段，等于0的蠕变模型用于描述加速蠕变阶段。在加速蠕变阶段，蠕变变形量随指数的变化而变化，随时间增长而迅速增大。岩体非线性黏弹塑性蠕变曲线见图9。对岩体施加应变0，且0＜s1＜s2＜10，可保持应变不变。因为NVPB模型没有具备松弛的特性，不管在什么时刻，应力和长期强度相等，此时，岩体的松弛特征与只有第1，2和3部分的松弛特性相似。当趋于无穷大时，。

1—σ0＜σs1; 2—σ0＜σs1≤σs2; 3—σ0＞σs2, n=1; 4—σ0＞σs2, n＞1。

3 考虑岩体蠕变数值计算单元

3.1 岩体蠕变模型分析

对于软岩，当应力为恒定0时，其典型蠕变曲线可分为3个部分[13]，如图10所示。从图10可见：

1)段上凸曲线为初期蠕变，曲线的斜率逐渐减小，表征岩体的蠕变速率逐渐降低；若施加的应力在这一阶段内骤降为0 kN，曲线则形成形态，且Fe，为0时的加载瞬时弹性应变；随着试验继续进行，岩样变形消失，材料依然保持弹性。

2)段为近似直线，其各点的斜率大致相同，为等速蠕变阶段。若将施加的应力在这一阶段骤降为0 kN，则曲线沿着曲线路径发展，该阶段存在不可恢复的塑性变形。

3)段为第3蠕变阶段。此阶段试样材料内部发生破坏，应变速率明显增大直至材料发生破坏。

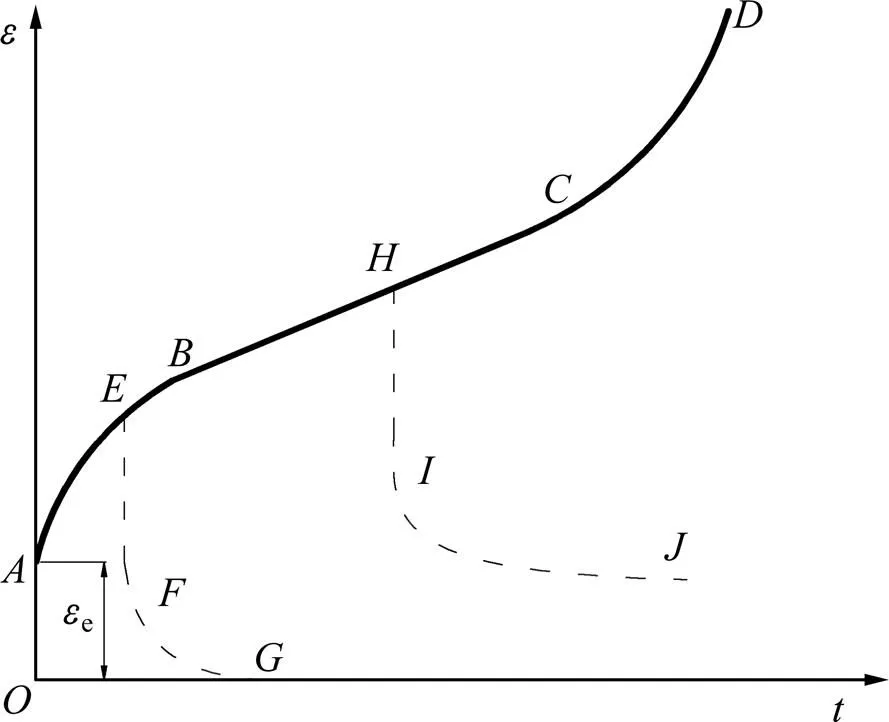
图10 典型蠕变曲线

一般地，瞬时变形都发生在蠕变曲线开始时。随着剪应力(以指数递减)速率增大，应变速率会逐渐稳定。通过实验结果可知，试样的变形特征与Burgers模型的蠕变曲线特征较吻合。如图11(a)所示，对于Maxwell模型与Kelvin模型组合成的Burgers模型，轴向应变受轴向应力作用时为

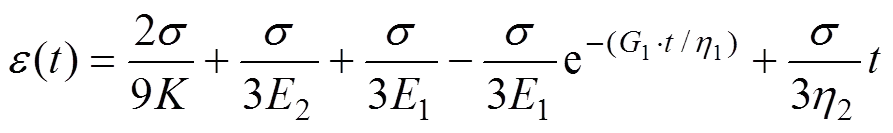
式中：为试样体积模量；1，2，1和2为Burgers模型中的黏弹性常量。

(a) 典型Burgers蠕变模型；(b) 蠕变曲线

图11 典型Burgers蠕变模型及其蠕变曲线

Fig. 11 Typical Burgers creep model and curve

3.2 黏弹对应性原则

在准静态载荷和小变形时，若用本构方程(积分型)来描述黏弹性体，则应力与应变、位移必须满足以下基本方程组。

平衡方程：

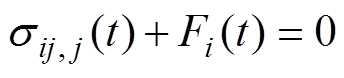
边界条件：

(13)

几何方程：

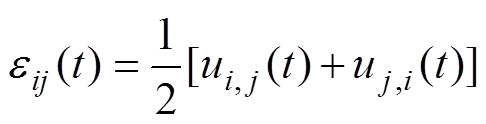
畸变方程：

(15)

体变方程：

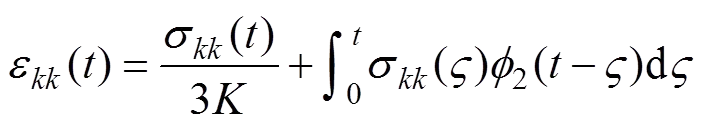
式中：S为的偏张量分量；e为ε的偏张量分量；2与分别为弹性的剪切模量和体积模量；1为剪切蠕变核；2为体变蠕变核(也称为记忆函数，为单元应力下的蠕变速度)。

对式(12)~式(16)分别通过单边拉普拉斯变换，得平衡方程：

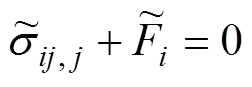
边界条件为

(18)

几何方程为

畸变方程为

(20)

体变方程为

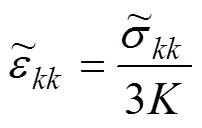
(22)

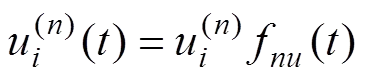
式中：为Ⅰ，Ⅱ和Ⅲ分别代表Ⅰ型裂纹，Ⅱ型裂纹和Ⅲ型裂纹；f()与f()分别为外加应力及位移的时间因子；为0时瞬时裂纹前缘应力；为0时瞬时裂纹前缘位移。可见：黏弹性的问题最后都可以由时间因子(()())的解来表示，时间因子因边界和蠕变模型不同而有所不同。

3.3 Burgers蠕变模型的数值计算

为反映软岩瞬弹性、瞬塑性、黏弹性及黏塑性特征共存的蠕变全过程，本文在Mohr−Coulomb准则的基础上提出一种新的塑性元件，称为M−C元件。在应力没有达到摩尔−库仑破坏准则时，该元件屈服应力s为0 MPa，而当≥s时，该元件则完全服从摩尔−库仑塑性流动规律。通过串联Burgers模型与该元件，形成了Burgers改进蠕变模型。该改进模型能够对黏弹塑性偏量特征及弹塑性体积进行模拟。各个元件具体的连接方式如图12所示。

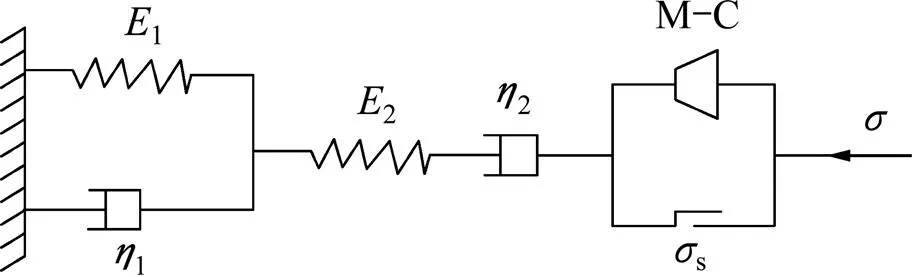
图12 Burgers改进蠕变模型

1) 当＜s时，黏弹塑性数值模型即为典型的Burgers蠕变模型。

2) 当≥s时，Burgers蠕变数值模型偏量行为可由以下关系描述。

总应变率：

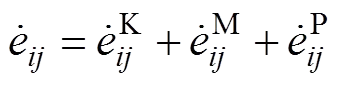
Kelvin体：

(25)

Maxwell体：

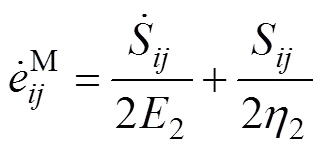
M−C元件体：

(27)

(29)

3.4 模型参数及验证

Burgers改进蠕变模型包含了典型Burgers元件的5个参数和M−C元件的黏结力С、内摩擦角和抗拉强度σ。其中，M−C元件的参数可通过材料的常规试验得到。

为得到Burgers蠕变模型的5个参数，假定各参数不随时间而变化，则应变速率在时间较大时即为常数。第2期蠕变曲线的渐近线即蠕变曲线为1条直线，有以下方程：

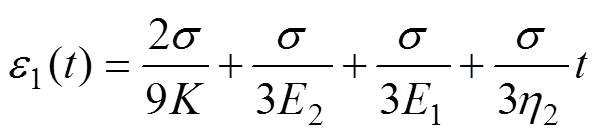
式中：当=0时，可得到该曲线在应变坐标轴上的截距为ε()。令为蠕变曲线和相应的渐近线之间的距离，容易从它们的几何关系得到

(31)

式中：为轴向应力；()为轴向应变；为蠕变时间。在半对数空间中，式(31)所示图形为1条直线，通过()和，可得到作用下的1和1，通过式(30)得到2。

为得到岩样的体积应变，可测量试验过程中岩样的轴向应变1和侧向应变2，即Δ/=1+22，应力平均值为/3，则

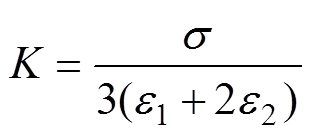
基于岩体蠕变试验结果，并通过上述方法，可得到岩体蠕变模型的各个参数，结果如表2所示。利用Burgers改进蠕变模型对岩样蠕变全程曲线进行拟合，并将拟合结果与蠕变试验结果进行对照。Burgers改进蠕变模型拟合曲线与蠕变试验曲线见图13。从图13可知：本文所建立的Burgers改进蠕变模型能较好地拟合岩体蠕变试验曲线，说明该模型具有一定的合 理性。

表2 模型拟合参数

注：为应力；1和2为弹性模量；1和2为黏滞系数；为体积模量；为黏聚力；为内摩擦角；t为抗拉强度。

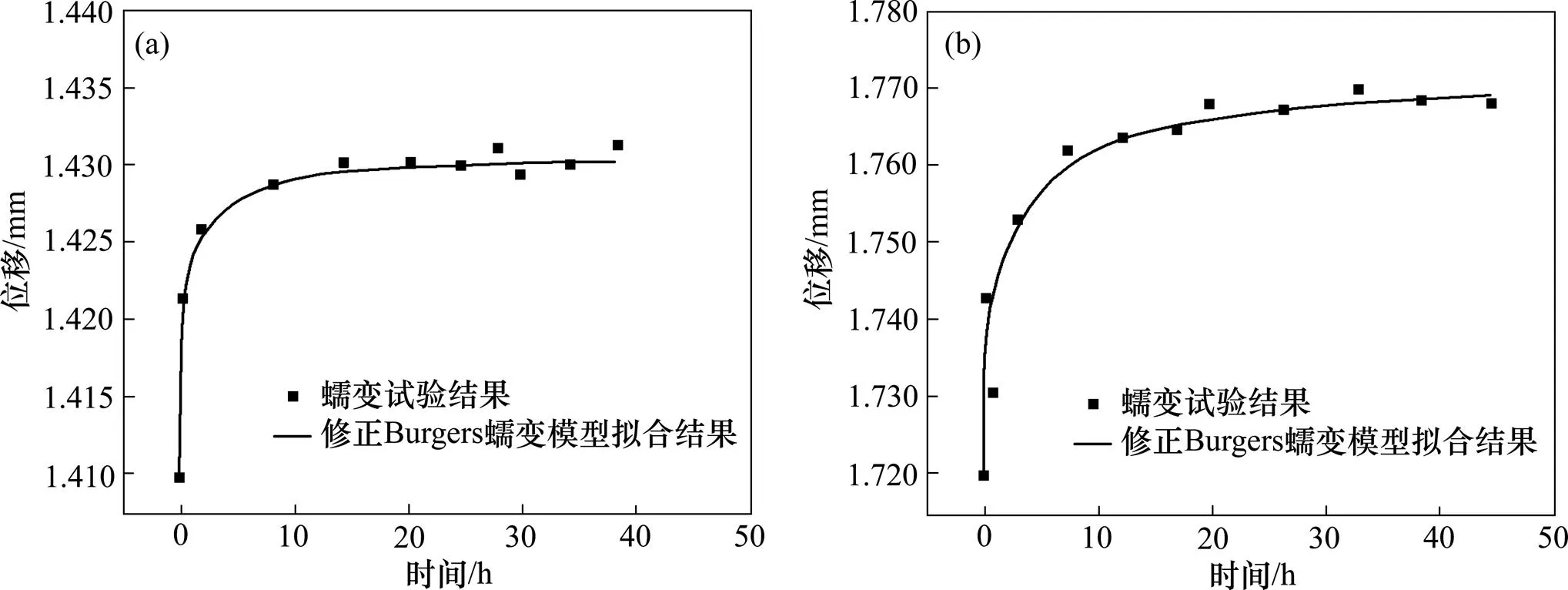
岩样类型：(a) 饱和白云片岩；(b) 饱和绿泥片岩

4 结论

1) 白云石英片岩和绿泥钠长片岩这2种岩样试件有明显的蠕变特性。在不同级别的加载下，加载应力与应变以比例方式增加。在较小应力下，这2种岩体材料的初始应变较明显，随着加载应力的增大而 增大。

2) 这2岩体材料同时具有黏塑、瞬塑、瞬弹和黏弹特性，这4种特性随着应力增加更加明显。

3) 这2种岩体材料饱水状态岩体蠕变现象更明显。在自然状态下，岩体材料处于稳定的蠕变范围，但在稳定状态临界点有较明显的加速蠕变现象。

4) 在Mohr−Coulomb准则基础上提出一种新的M−C塑性元件，串联Burgers模型与该元件，形成Burgers改进蠕变模型。该改进模型能对黏弹塑性偏量特征及弹塑性体积进行模拟，为岩体边坡稳定性的时间效应研究提供了理论依据。

[1] 陈有亮, 孙钧.岩石的流变断裂特性[J].岩石力学与工程学报, 1996, 15(4): 323−327. CHEN Youliang, SUN Jun. Creep fracture of rook[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(4): 323−327.

[2] 杨淑碧, 徐进, 董孝璧. 红层地区砂泥岩互层状斜坡岩体流变特性研究[J]. 地质灾害与环境保护, 1996, 7(2): 12−24. YANG Shubi, XU Jin, DONG Xiaobi. Rheological feature of slope rockmass composed of alternating beds of sandstone and mudstone in redbeds area[J]. Journal of Geological Harzards and Enviroment Preservation, 1996, 7(2): 12−24.

[3] 赵永辉, 何之民, 沈明荣. 润扬大桥北锚碇岩石流变特性的试验研究[J]. 岩土力学, 2003, 24(4): 583−586. ZHAO Yonghui, HE Zhimin, SHEN Mingrong. Testingstudy on rockrheologicalcharacteristic of northanchor block of Runyang bridge[J]. Rock and Soil Mechanics, 2003, 24(4): 583−586.

[4] SUN Jun, HU Yuyin. Time-dependent effects on the tensile strength of saturated granite at Three Georges Project in China[J]. International of rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1997, 34(3): 381−384.

[5] 徐平, 夏熙伦. 三峡枢纽岩体结构面蠕变模型初步研究[J]. 长江科学院院报, 1992, 9(1): 42−46. XU Ping, XIA Xilun. A study on the creep model of rock mass discontinuity of the three gorges project[J]. Journal of Yangtze River Scientific Research Institute, 1992, 9(1): 42−46.

[6] 李连崇, 李少华, 李宏. 基于岩石长期强度特征的岩质边坡时效变形过程分析[J]. 岩土工程学报, 2014, 36(1): 47−56. LI Lianchong, LI Shaohua, LI Hong. Time-dependent deformation of rock slopes based on long-term strength characteristics of rocks[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 47−56.

[7] 刘光廷, 胡昱, 陈凤岐, 等. 软岩多轴流变特性及其对拱坝的影响[J]. 岩石力学与工程学报, 2004, 23(8): 1237−1241. LIU Guangting, HU Yu, CHEN Fengqi. Rheological property of soft rock under multiaxial compression and its effect on design of arch dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1237−1241.

[8] 佘成学, 孙辅庭. 节理岩体黏弹塑性流变破坏模型研究[J]. 岩石力学与工程学报, 2013, 32(2): 231−238. SHE Chengxue, SUN Futing. Research on visco-elastoplastic rheological failure model of jointed rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 231−238.

[9] 王明芳, 胡斌, 蒋海飞. 花岗岩剪切流变力学特性试验与模型[J]. 中南大学学报(自然科学版), 2014, 45(9): 3111−3120. WANG Mingfan, HU Bin, JIANG Haifei, et al. Experiment and model investigation on shear rheological mechanical properties of granite[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 1916−1922.

[10] 刘东燕, 蒋海飞, 李东升, 等. 高围压高孔隙水压作用下岩石蠕变特性[J]. 中南大学学报(自然科学版), 2014, 45(6): 3111−3120. LIU Dongyan, JIANG Haifei, LI Dongsheng, et al. Creep properties of rock under high confining pressure and high water pore pressure[J]. Journal of Central South University (Science and Technology), 2014, 45(6): 1916−1922.

[11] 杨振伟, 金爱民, 周喻, 等. 伯格斯模型参数调试与岩石蠕变特性颗粒流分析[J]. 岩土力学, 2015, 36(1): 240−248. YANG Zhenwei, JIN Aimin, ZHOU Yu, et al. Parametric analysis of Burgers model and creep properties of rock with particle flow code[J]. Rock and Soil Mechanics,2015, 36(1): 240−248.

[12] 杨圣奇. 岩石流变力学特性的研究及其工程应用[D]. 南京: 河海大学水利水电学院, 2006: 33−54. YANG Shenqi. Study on the rheological properties of rock and its engineering application[D]. Nanjing: Hohai University. College of Water Conservancy and Hydropower Engineering, 2006: 33−54.

[13] 徐志英. 岩石力学[M]. 北京: 中国水利水电出版社, 1997: 23−135. XU Zhiying. Rock mechanics[M]. Beijing: China Water and Power Press, 1997: 23−135.

[14] 张淳源. 黏弹性断裂力学[M]. 武汉: 华中理工大学出版社, 1994: 49−149. ZHANG Chunyuan. Viscoelastic fracture mechanics[M]. Wuhan: Huazhong University of Technology Press, 1997: 49−149.

[15] 袁龙蔚, 智荣斌, 李之达. 流变断裂学基础[M]. 北京: 国防工业出版社, 1992: 40−59. YUAN Longwei, ZHI Rongbin, LI Zhida. Rheological fracture theory[M]. Beijing: National Defend Industry Press, 1992: 40−59.

[16] 韩旭, 吴立, 李波, 等. 考虑蠕变效应的软岩特大断面隧道围岩抗力系数计算[J]. 科学技术与工程, 2014, 14(21): 146−151. HAN Xu, WU Li, Li Bo, et al. Calculation on rock resistant coefficient of large section soft rock tunnel considering creep effect[J]. Science Technology and Engineering, 2014, 14(21): 146−151.

(编辑 陈灿华)

Research on improved Burgers model based on rock mass creep test

TANG Jia1, 2, PENG Zhenbin1, HE Zhongming3

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;2. Geological Engineering Department, Powerchina Zhongnan Engineering Corporation Limited, Changsha 410007, China;3. School of Traffic and Transportation Engineering, Changsha University of Science and Technology, Changsha 410076, China)

Taking Hubei Pankou hydropower station intake rock slope as object, creep test in laboratory was made to obtain the stress strain curve of rock mass and the corresponding mechanical parameters. The constitutive model was analyzed and an improvement method was proposed. A new M−C plastic component was introduced and the Burgers improved creep was proposed. The results show that muscovite quartz schist and sodium chlorite schist have obvious creep properties. At different levels of load stress, load stress and strain increase proportionately, and the two kinds of rock mass materials possess the characteristics of viscous-plastic, instantaneous-plastic, instantaneous-elastic and viscous-elastic. The four properties improve with the increase of the stress. The creep phenomenon of the two kinds of rock mass materials is more obvious in saturation condition. The Burgers improved creep can simulate the viscoelastic plastic displacement characteristics and the elastic-plastic volume behavior.

rock mass; creep property; M−C plastic component; improved model

10.11817/j.issn.1672-7207.2017.09.021

TU457

A

1672−7207(2017)09−2414−11

2016−10−09；

2016−12−07

国家自然科学基金资助项目(51508042) (Project(51508042) supported by the National Natural Science Foundation of China)

彭振斌，教授，博士生导师，从事地质工程、岩土工程研究；E-mail: zbp9040@sina.com