Structural Design Exploration on Double Intersecting Spheres Manned Pressure Hull of Full Ocean Depth

LI Hao,WANG Fang,CUI Wei-cheng(.China Ship Scientific Research Center,Wuxi 408,China;.Hadal Science and Technology Research Center,College of Marine Science,Shanghai Ocean University(Shanghai Engineering Research Center of Hadal Science and Technology),Shanghai 0306,China)

Structural Design Exploration on Double Intersecting Spheres Manned Pressure Hull of Full Ocean Depth

LI Hao1,WANG Fang2,CUI Wei-cheng2
(1.China Ship Scientific Research Center,Wuxi 214082,China;2.Hadal Science and Technology Research Center,College of Marine Science,Shanghai Ocean University(Shanghai Engineering Research Center of Hadal Science and Technology),Shanghai 201306,China)

Abstract:Titanium alloy spherical pressure hull is widely used for deep-sea manned submersible.However,due to constraint of strength of titanium alloy,if full-ocean-depth submersible is designed to have enough volume to take three occupants and Ti-6Al-4V ELI is used,pressure hull thickness will exceed current manufactural ability of most countries.To solve this problem and explore possible form of full-ocean-depth manned pressure hull,based on finite element analysis(by ANSYS),a novel pressure hull structure of double intersecting spheres is proposed,and an optimization for this structure is carried out.Strength under operating pressure and ultimate strength are used as design constraints to ensure structural strength of the whole structure.Also,a comparison between pressure hull forms of the double intersecting spheres and traditional single sphere is presented.

Key words:deep manned submersible;pressure hull;titanium alloy;Ti-6Al-4V ELI;full ocean depth;double intersecting spheres

0 Introduction

Deep-sea manned submersible is the core equipment of ocean scientific research at deepsea space.Significant advantages of deep-sea manned submersibles comparing to unmanned submersibles are strong operational abilities at deep seabed and allowing researchers to be personally on the scene.Up to now several 4 500-7 000 m level deep-sea submersibles have already been used to carry out routine scientific research.Based on achievements of building 4 500-7 000 m level manned submersibles,more and more researchers pay attention to fullocean-depth manned submersible(FODMS)which is a logically derivative of 4 500-7 000 m level submersible,and the idea of‘Third-generation Full-ocean-depth Manned Submersible(third-generation FODMS)’is purposed[1].The most significant characteristics of the thirdgeneration FODMS which distinguish it from its previous counterparts include its strong operational ability and its capability to dive down and float up with a vertical speed of at least 3 knots.The first-generation FODMSs have no or very weak scientific operational ability and move slowly in ocean while the second-generation FODMSs dive down and float up with a vertical speed of less than 2 knots.

These new characteristics,or called requirements,for FODMS bring new challenges to submersible designers.For design of manned pressure hull,it is required that manned pressure hull should have enough volume to contain 2-3 occupants to ensure operational ability of submersible and be strong enough to resist water pressure at full-ocean-depth seabed.It is also important to balance hull’s size and hydrodynamic performance of submersible due to high requirement for diving speed.To solve these new challenges,some organizations came up with novel ideas[2-4]on design of manned pressure hull,for example,full glass pressure hull,half glass-half titanium alloy pressure hull,carbon fiber pressure hull,and so on.

Double intersecting spheres manned pressure hull(DSMPH)is also a promising design form of interests.Compared with single spherical hull and cylindrical hull,which are widely used on current manned submersibles,DSMPH has some important advantages.Firstly,it combines small volume density,the advantage of sphere hull,with high space utilization rate,the advantage of cylinder hull.Secondly,compared with single spherical hull of the same volume,DSMPH’s each spherical hull has smaller radial size and smaller hull thickness which makes manufacture easier.Thirdly,compared with single spherical hull of the same volume,DSMPH has a smaller length-diameter ratio,which is good for hydrodynamic performance and general arrangement of submersible.Fourthly,it is easy to insulate crew from dangerous equipment in DSMPH.

Due to the advantages of DSMPH,some researchers have investigated possible structural forms of DSMPH.Liang et al[5]investigated a pressure hull optimum design of 3 000 m multiple intersecting spheres.This hull consisted of shells and shell stiffeners.Stresses,displacement,and ultimate strength of the structure were all calculated by analytical formulas in their research.Jen and Lai[6]further studied the transient response of this pressure hull subjected to underwater explosion in shallow water.Based on finite element analysis,Wu[7]presented a pressure hull design of three intersecting spheres.Formulas were proposed for calculating maximal stress and ultimate strength.Characteristic of Wu’s design was that there were not any stiffeners on both spherical hull and connecting part,and the whole hull consisted of smooth arc shell of uniform thickness.

In this paper,a novel structural design of DSMPH with titanium alloy Ti-6Al-4V ELI is proposed.Referring to Refs.[8-9],the strength and ultimate strength of pressure hull are checked by finite element analysis(using ANSYS).Subjected to constraints of strength and ultimate strength,with geometry parameters of pressure hull as variables and mass of structure as optimization objective,optimization of DSMPH is carried out(using Isight).Basic properties of optimized DSMPH are compared with those of a single sphere pressure hull of the same effectivevolume at the end.

1 Design of DSMPH and strength analysis standard

1.1 Pressure hull design of titanium alloy double intersecting spheres

A standard design of 7 000 m-level manned pressure hull with a hatch is presented in Fig.1.This design form has been studied by many researchers,came into use for years and was proved reliable.The merit of this design is that if geometry parameters of transition part between hatch and main spherical hull are well designed,ultimate strength of main sphere will not be obviously damaged by the existence of hatch[10].

Fig.1 Design of 7 000 m-level deep-sea manned pressure hull with a hatch

Based on the design in Fig.1,a design of titanium alloy DSMPH consisting of two spherical hulls and connecting part is presented in Fig.2.For spherical hulls,geometry parameters are inner radiuses R1,R2and thickness t1,t2.For connecting part,geometry parameters include those representing the sizes of connecting part(length L,inner radius R,thickness T,θ1,θ2)and those representing the transition part between connecting part and spherical hulls(α1,α2,β1,β2).

Fig.2 (a)Geometry design of DSMPH

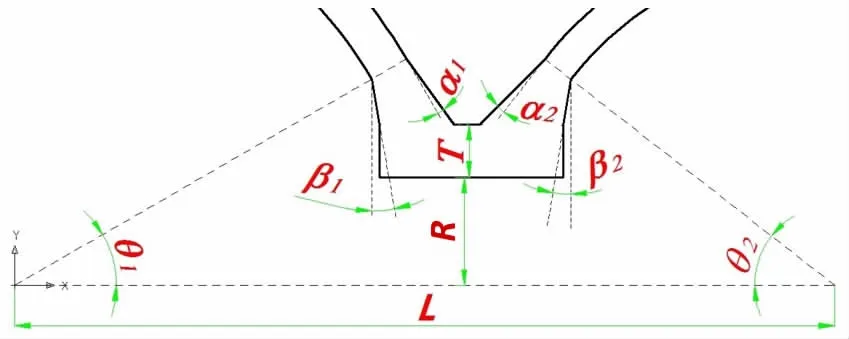
Fig.2 (b)Geometry parameters of connecting part

1.2 Basic input parameters

The maximum operating pressure:

The maximum operating pressure for FODMS at 11 000 m-depth seabed is calculated by

P= ρmgh=1 052×9.8×11 000=113.4 MPa

where ρmis seawater density,kg/m3.

Material:

The material used in this investigation is Ti-6AL-4V ELI(See Tab.1).σyis the yielding stress,σuis the ultimate tensile stress.E is Young’s modulus.

Tab.1 Material properties of Ti-6Al-4V ELI

1.3 Strength analysis standard

Referring to Rules for Building and Classing of Diving System and Submersible of China Classification Society(CCS)[8]and Ref.[9],herein strength and ultimate strength are used as strength analysis standard to check structural design of DSMPH.It is required as follows.

Requirement on ultimate strength:

Re.1 The ultimate strength of the whole structure should be greater than 1.5×P,i.e.,the safety factor for the ultimate strength is 1.5,where P is maximum operating pressure.

Requirements on strength,or called stress limitations:

Re.2 The average shell membrane stress at maximum operating pressure will be limited to 2/3 of the yield strength of material.

Re.3 The highest combined value of average shell membrane stress and bending stress(excluding effects of local stress concentrations)at maximum operating pressure will be limited to 3/4 of the yield strength of material.

Re.4 The maximum compressive peak stress at any point of the hull,including effects of local stress concentrations,will be limited to 4/3 of the yield strength of material and will not exceed the ultimate strength of material.The maximum tensile peak stress at any point of the hull,including effects of local stress concentrations,will be limited to the yield strength of material.

Re.5 For cylindrical part of connecting part,average circumferential stress at midpoint of cylinder should be less than 0.85 of yield strength of material.

Re.6 For cylindrical part of connecting part,average axial stress at endpoints of cylinder should be less than 1.15 of yield strength of material.

Res.1-6 form the complete strength standard,or called strength constraints,for design of DSMPH.Similar standard is also used to check strength of a single sphere pressure hull in Chap.3 of this paper.

1.4 Determination of some parameters

Considering practical need of containing 2-3 occupants,the radii of spheres are set to be R1=800 mm and R2=650 mm.The bigger hull can contain two occupants and the smaller one can hold one occupant.

Since additional parts like penetration holes and hatches will break the intactness of spherical hull and more or less damage the strength of spherical hull,the thickness of each spherical hull should be greater than minimal thickness of its intact counterpart.Tab.2 shows the minimal thickness of intact spherical hulls under constraint of just ultimate strength(Re.1),which is done using ANSYS.Thus,t1≥84 mm,t2≥68 mm.

Tab.2 Minimal thickness of intact spherical hull under constraint of ultimate strength

Inner radius of connecting part R is another important parameter,which decides to what extent the intactness of original intact spherical hull will be damaged.Based on 10 trial optimizations(similar to the optimization in Chap.2),it is found that optimization algorithm always prefer the smallest R in its variation range(for example 270-360 mm),which means the greater the value of R is,the heavier the structure is.So,it is reasonable to choose the smallest value of R,which also make it easy for occupants to go through the connecting part.Herein,R is set to be 285 mm.

2 Optimization

The mass of manned pressure hull makes up more than 1/3 of total mass of submersible.Decreasing mass of manned pressure hull has important contribution to realize the two core characteristics of the third-generation FODMS mentioned in Chap.0.Thus,reducing mass is a main goal of DSMPH design.

In Chap.2,a design of DSMPH and a strength analysis standard are presented.However it is not easy to manually find a good set of parameters which satisfies strength analysis standard and is also material-saving.So,an optimization problem needs to be solved to find a goodset of parameters with which the DSMPH has small mass and strong structural strength.This optimization problem is summarized as follows.

Objective:Minimizing mass

Constraints:Stress distributions at maximum operating pressure(Res.2-6)

Variables and range:Listed in Tab.3.

Tab.3 Optimization variables and upper and lower bound

It should be noted that Re.1 is used to calculate the lower bound of the sphere thickness t1and t2and then it is excluded from the constraints of this optimization problem.This could greatly reduce computational burden because calculating ultimate strength is a nonlinear problem and is time-consuming which costs about 50 minutes for one case.

However,Re.1 is still a very important requirement for structural design.The way to make Re.1 satisfied is the following.For ultimate strength of each spherical hull,previous experience reveals if each originally intact spherical hull satisfied Re.1,existence of connecting part will not obviously damage ultimate strength of spherical hull as long as the whole structure satisfy strength requirement,that is,Res.2-6.For ultimate strength of connecting part,it is observed that size of connecting part is much smaller than those of two spherical hulls,which means the stability of it should be better than that of spherical hulls.As long as Res.2-6 are satisfied for connecting part,which to a large extent ensures the ultimate strength of connecting part,it is more likely that final collapse will first occur on spherical hulls.To double check ultimate strength of final optimized design,ultimate strength of the whole structure of optimized design is calculated(see Fig.3,Tab.5-b).

The minimum values of variation range of t1,t2in Tab.3 are greater than their counterparts in Tab.2.It is because that trial calculation reveals that,for DSMPH and spherical models of this paper,strength requirement(Res.2-6)is stricter than ultimate strength requirement(Re.1).Thus,in order to satisfy Res.2-6,t1,t2are set to be greater than 84 mm and 68 mm correspondingly.

In this optimization problem,relationship between the variables is complicated.And optimization space is discontinuous,because for some combination of variables,it fails to set up geometry model.To handle the complication of this optimization problem,Multi-Islands Genetic Algorithm(MIGA)is used,which has a strong ability to explore the whole optimization space and thus can prevent the calculation from dropping into local optimal solution too early.A widely accepted optimization software,Isight,is chosen to control the whole procedure(see Fig.3).

The optimization parameters of MIGA are shown in Tab.4.MIGA explores 14002 cases and the history of optimization objective is illustrated in Fig.4.The optimal point is obtained at the 12900th run(marked by a star in Fig.4).

Tab.4 Optimization parameters for Multi-Island Genetic Algorithm

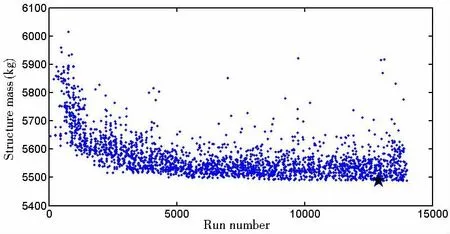
Fig.4 History of structural mass(kg).Star is the optimized point

3 Result and discussion

The design of final optimized point is shown in Fig.5 and Tab.5.It is observed from optimization history(not shown in this paper)that the core constraint which makes most unfeasible cases fail is Re.4.And the area with maximal stress is inner surface of connecting part.Some calculation details can be referred to Ref.[11].It means that a main work of designingDSMPH done by Isight is to configure a good set of geometry parameters to make the stress level of inner surface of connecting part small enough.

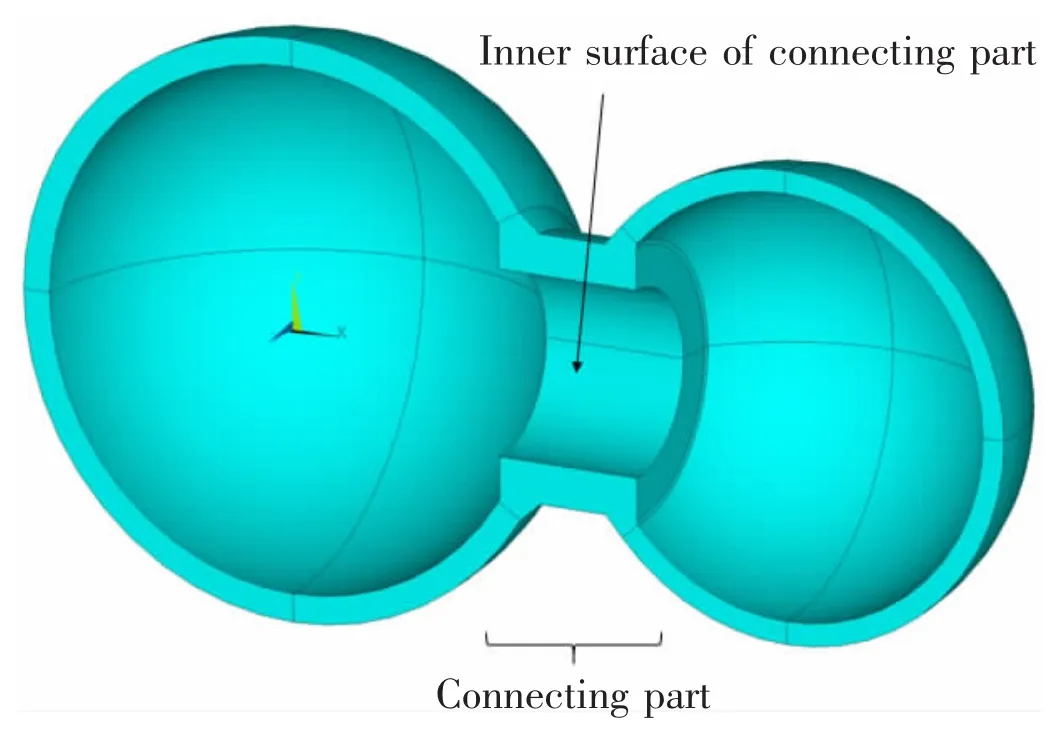
Fig.5 Optimized DSMPH

Tab.5 -a Optimized DSMPH

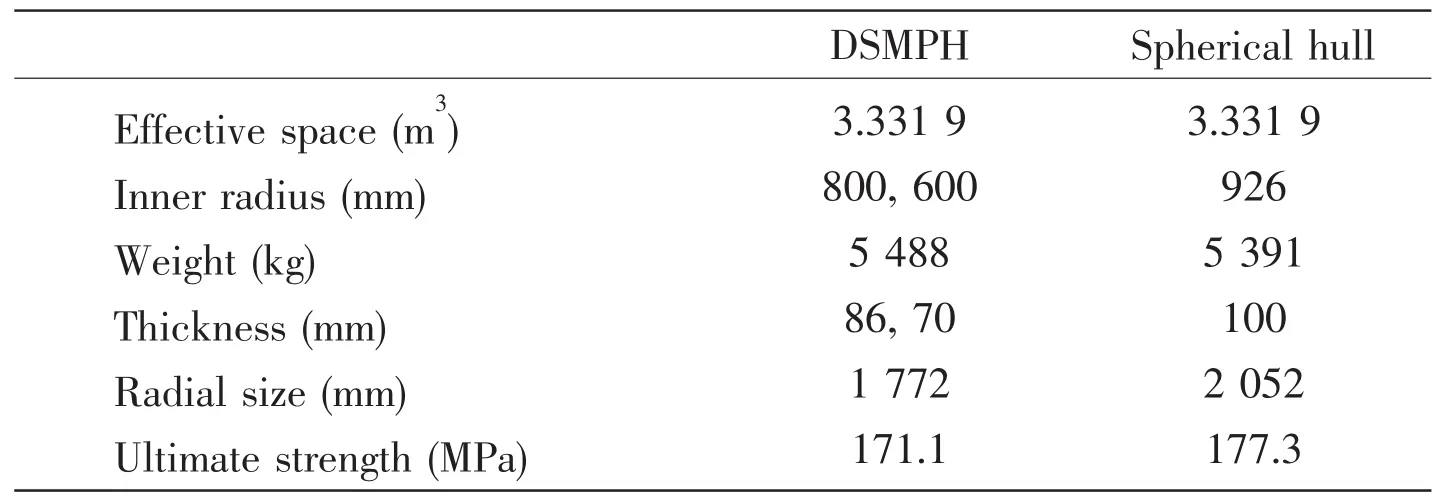
Tab.5 -b Optimized DSMPH and optimized spherical hull with the same effective volume

Optimized DSMPH provides 3.331 9 m3effective volume.To further study DSMPH,optimized DSMPH is compared with an optimized spherical hull(see Tab.5-b),which has the same effective volume.The thickness of spherical hull is determined by the same optimization procedure shown in Fig.3,with constraints Res.1-6,optimization objective-structural mass.From Tab.5,the optimized DSMPH is heavier than the optimized single spherical hull by 1.8%.In this case,adopting DSMPH can reduce radial size of pressure hull by 13.6%.The hull thickness of DSMPH is thinner than that of single spherical hull by 14 mm.All of these indicate that DSMPH can significantly benefit hydrodynamic performance and manufacture of submersible,and it increases mass by just 1.8%.

Comparing Tab.5 with Tab.2,it is observed that optimized design subjected to the strength requirements,that is,Res.2-6,can satisfy the requirement of ultimate strength,that is,Re.6,with a significant allowance.The same thing can also be found by checking optimization historyof variables(not shown in this paper)in the case of DSMPH.It means that it is a reasonable way to design and optimize full-ocean-depth pressure hull by strength requirements,and finally check the optimized design by ultimate strength.In this way,nonlinear problem needs just be solved once,and designers can focus on linear analyses which are much easier.

Acknowledgment

Professor Hu Yong and Doctor Pan Binbin both from Shanghai Ocean University,and Mr.Yu Jun,from China Ship Scientific Research Center,provided useful suggestions and help.We thank all of them.

[1]Li Z W.Research on part of key technologies for the third generation of manned submersibles with full ocean depth[D].M.Sc thesis,China Ship Research and Development Academy,Beijing,China,2013.(in Chinese)

[2]Jamieson A J,Fujii T,Mayor D J,Solan M,Priede I G.Hadal trenches:The ecology of the deepest places on Earth[J].Trends in Ecology&Evolution,2010,25(3):190-197.

[3]Hawkes G.The old arguments of manned versus unmanned systems are about to become irrelevant:New technologies are game changers[J].Marine Technology Society Journal,2009,43(5):164-168.

[4]Taylor L,Lawson T.Project deepsearch:An innovative solution for accessing the oceans[J].Marine Technology Society Journal,2009,43(5):169-178.

[5]Liang C C,Shiah S W,Jen C Y,Chen H W.Optimum design of multiple intersecting spheres deep-submerged pressure hull[J].Ocean Engineering,2004,31:447-457.

[6]Jen C Y,Lai W H.Transient response of multiple intersecting spheres of deep-submerged pressure hull subjected to underwater explosion[J].Theoretical and Applied Fracture Mechanics,2007,48:112-126.

[7]Wu L.The response analysis and optimum design of great deep-submerged pressure hulls[D].Huazhong University of Science and Technology,Wuhan,China,2007.(in Chinese)

[8]Rules for the classification and construction of diving systems and submersibles[S].China Classification Society(CCS),Beijing,China,2013.(in Chinese)

[9]Pan B B,Cui W C.Structural optimization for a spherical pressure hull of a deep manned submersible based on an appropriate design standard[J].IEEE Journal of Oceanic Engineering,2012,37(3):564-571.

[10]Lu B.Ultimate strength analysis of pressure spherical hull in deep-sea manned submersibles[D].Shanghai Jiao Tong U-niversity,Shanghai,China,2004.(in Chinese)

[11]Li H.Research on resistance performance and structure of manned pressure hull of the third-generation full-oceandepth manned submersible[D].M.Sc Thesis,China Ship Research and Development Academy,Beijing,China,2014.(in Chinese)

全海深双球连接耐压舱的结构设计探索

李 浩1，王 芳2，崔维成2
（1.中国船舶科学研究中心，江苏 无锡214082；2.上海海洋大学 深渊科学技术研究中心（上海深渊科学工程技术研究中心），上海201306）

钛合金耐压球壳被广泛地应用于大深度载人潜水器。但是，由于受到材料强度的限制，若采用成熟的Ti-6Al-4VELI来设计3人型的全海深载人舱，其壁厚将超出很多国家的现有制造能力。为了解决这一矛盾，该文提出了一种新的双球连接的方案，并以中国船级社最新的强度标准作为优化约束条件，用有限元分析法对这种结构形式进行了优化设计。最后，对双球结构方案与传统单球方案作了比较。

载人深潜器；载人舱；钛合金；Ti-6Al-4V ELI；全海深；双球连接壳

U661.4

A

李 浩（1988-），男，中国船舶科学研究中心硕士研究生；王 芳（1979-），女，博士，上海海洋大学副研究员；崔维成（1963-），男，博士，上海海洋大学教授，博士生导师。

10.3969/j.issn.1007-7294.2017.09.010

Article ID： 1007-7294（2017）09-1160-10

Received date：2017-03-03

Foundation item:Supported by the State Key Program of National Natural Science of China(Project No.51439004);The general Program of National Natural Science Foundation of China(Project No.51679133);The scientific innovation program project by the Shanghai Committee of Science and Technology(Project No.15DZ1207000)

Biography：LI Hao(1988-),male,master student of China Ship Scientific Research Center,E-mail:lihaocq@umich.edu;WANG Fang(1979-),female,Ph.D.,associate professor of Shanghai Ocean University;CUI Wei-cheng(1963-),male,Ph.D.professor/tutor of Shanghai Ocean University.