Using a Simple Method for Singularity Avoidance in Thrust Allocation for Marine Vessels

XU Sheng-wen,WANG Xue-feng,WANG Lei,LI Bo,ZHOU Li

(1.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE),Shanghai 200240,China;3.School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;4.School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang,212003,China)

Using a Simple Method for Singularity Avoidance in Thrust Allocation for Marine Vessels

XU Sheng-wen1,2,3,WANG Xue-feng1,2,3,WANG Lei1,2,3,LI Bo1,2,3,ZHOU Li4

(1.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE),Shanghai 200240,China;3.School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;4.School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang,212003,China)

Abstract:The vessel with singular configuration may suddenly loses its position since the required forces cannot be timely achieved.In this paper,a simple method which can avoid singularity configuration in thrust allocation is proposed.The performance of the new method was demonstrated by a time domain simulation for a semi-submersible.The simulation employed two different singularity avoidance methods including the new method and a typical method that was widely used in literature.The results show that the new proposed method can achieve the same good performance as the aforementioned typical method.And using the simple method,the elapsed time for simulation is largely suppressed,although the consumed power has a slight rise.The higher efficiency of the simple method can ensure this method more adaptive in real-time thrust allocation of dynamic positioning for marine vessels.

Key words:thrust allocation logic;singularity avoidance;simple method;real-time

0 Introduction

A dynamically positioned(DP)vessel is by the International Maritime Organization(IMO)and the certifying class societies(DNV,ABS,LR,etc.)defined as a vessel that maintains its position and heading(fixed position or pre-determined track)exclusively by means of active thrusters.Over the last five decades,dynamic positioning system(DPS)in deep water has been used in the marine sector,oil and gas industries,military services in many tasks such as drilling,oil and gas floating production platforms,cable and pipe laying,docking and towing,side by side arrangement of FPSO and shuttle tanker,see Mahfouz and El-Tahan(2006)[1].Each of these operations benefits from a DPS’s ability to include precise position-keeping,freedom from the restrictions of mooring spread systems,the ability to move quickly from one site to another,apply easily to any depth of water and track-keeping capabilities.

Thrust allocation logic,as an essentially important module of DPS,allocates the commanded thrust forces generated by the higher level controller among all available thrusters.Thrust allocation problem has been studied by many researchers in literature.A survey of control allocation methods for ships and underwater vehicles can be found in Fossen and Johansen(2006)[2].Thrust allocation problem has been formulated as a constrained optimization problem,where the objective is to minimize power consumption and the gap between commanded forces and achieved forces,subjected to constraints such as thruster position limits,see Enns(1998)[3],Bodson(2002)[4]and Durham(1993)[5].Further,the solving of the constrained optimization problem in real time has been addressed by Harkegard(2002)[6]and Johansen(2004)[7].

In thrust allocation,a singular configuration is when the orientation of the thrusters makes it impossible to produce generalized thrust forces in all directions.Singularity problem particularly exists in thrust allocation for vessels with low rotation speeds thrusters.Thus,the response time of the thrusters to changes in the commanded generalized force may be too slow.There are several methods in literature to avoid singularity configuration,see Johansen(2004)[7]and Ruth(2008)[8].However,the present methods may be time-consuming since the criterion of the thrust allocation problem becomes rather complicated when employing these methods.Since the thrust allocation problem should be solved at every sample time,the efficiency of solving the problem is very important for a safety-critical real time system with limiting processing capability and high demands for program reliability.

The main objective of this paper is that the criterion of the thrust allocation problem includes a simple term that penalizes the singular configuration.For thrust system with only azimuth thrusters,the particular singularity configuration is that all thrusters have one same direction.The simple method can penalize the situation when the thrusters has equal directions.However,the simple method here is not limited to be applied for thrust system with only azimuth thrusters,since any thruster can be seen as an azimuth thruster when its thrust force and direction at the specific sample are provided.

The simple method is expected to make the thrust allocation problem to be more efficient than that with existing methods.The performance of the simple method was demonstrated by a time-domain simulation for a semi-submersible with 8 azimuth thrusters.The simulation employed two different singularity avoidance methods including the new method and a typical method that has been addressed by Johansen(2004)[7].

This paper is logically constructed in 6 chapters.Chap.1 contains an introduction to the singularity configuration in thrust allocation.In Chap.2,the thrust allocation logic considering singularity avoidance is presented by an explanation of Johansen’s method.An analysis on the computation effort of this method is also addressed.Chap.3 gives a simple method for singularity avoidance in thrust allocation logic,followed by an analysis on the computation effort.Chap.4 is about a time domain simulation for a semi-submersible.In Chap.5,the simulation results and corresponding discussions are presented.Finally,conclusions are drawn in Chap.6.

1 A singular configuration

1.1 Coordinate

The coordinate system is fixed to the vessel body with the origin located at the mean oscillatory position in the average water plane with X axis points towards bow,Y axis points towards port and Z axis points towards upwards.The relative environmental force angle,α,is positive anti-clockwise starting from the stern.Moments are positive anti-clockwise.The coordinate system is illustrated in Fig.1.

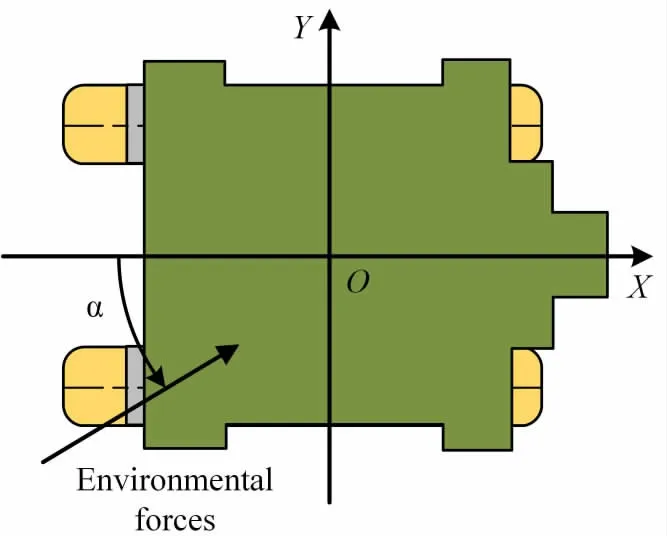
Fig.1 Coordinate of the vessel

1.2 3-DOF configuration

A characteristic feature of thrust allocation problems is that there are more thrusters than enough to generate the commanded forces and moment,such that there are many feasible solutions to supply the forces and moment.Thrust allocation logic must be employed to determine the best one among all feasible solutions.

Considering a marine vessel equipped with m azimuth thrusters,the generalized force vectorproduced jointly by the thrusters is given by

The location of the i-th thruster in the vessel isin the body-fixed coordinate system.

1.3 A singularity configuration

In thrust allocation of DPS,a singular configuration is when the orientation of the thrusters makes it impossible to produce generalized thrust forces in all directions.Singularity problem particularly exists in thrust allocation for vessels with low rotation speeds thrusters.Thus,the response time of the thrusters to changes in the commanded generalized force may be too slow.In moderate sea states,the singularity configuration has the advantage of saving energy since the thrust force directly compensates the environmental forces.However,in severe seastates,a sudden drift off may occur when the required thrust force cannot be attained in one of generalized directions.A singular configuration is crucially dangerous in thrust allocation from this point.

Mathematically,the thruster configuration matrixdoes not have full rank indicates the configuration is singular.Particularly,for vessel with only azimuth thrusters,the singularity configuration is that all thrusters have one same direction,as shown in Fig.2.In this circumstance,the rank of the configuration matrixis at most 2,which is less than the full rank 3.In order to avoid singularity configuration,this situation should be penalized in thrust allocation logic.

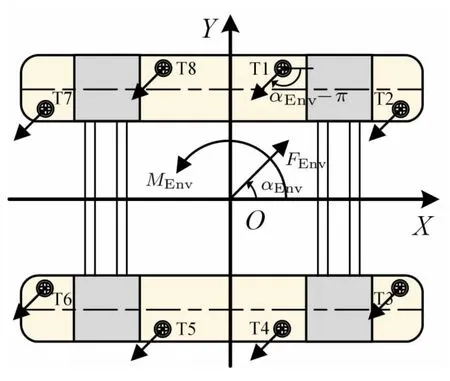
Fig.2 An example of singularity configuration for vessel with only azimuth thrusters

2 Thrust allocation logic

2.1 Johansen’s method

Thrust allocation problem can be formulated as an optimization problem,where the objective is typically to minimize the use of the control power and the gap between the commanded and achieved forces subjected to thruster rate and other operational constraints.The commanded forces(including moment)come from the corresponding control law.

Johansen(2004)[7]proposed a constrained nonlinear control allocation method with singularity avoidance.The method penalizes the situation that a singular configuration occurs or nearly occurs.In a near singular configuration,some thruster may be easily saturated and the commanded generalized force cannot be attained.In order to make the thrust allocation robust and avoid near-singular configurations,is not close to singular is introduced in the criterion of the optimization problem.The item that should be included in the criterion can be represented by

where ε＞0 is required to avoid numerical problems and ρ＞0 is a weighting parameter.The item(Eq.(3))should be minimized subjected to thruster constraints.When the configuration is near singular configuration,the item becomes very large since detis near to 0.And the near singular configuration will then be excluded from the solution.

The optimization problem becomes a nonlinear problem since the item in Eq.(3)is nonlinear.It requires a significant amount of computation at each sample to solve the nonlinearproblem.In order to implement this singularity configuration adequately,a locally convex quadratic programming(QP)reformulation is suggested.And the following optimization problem is defined.

where Wiand uiare the i-th thruster’s consumed power and thrust force,respectively.△α,△u are the azimuth thruster’s angle and thrust difference between this sample and the last sample,respectively.The second termin Eq.(4)penalizes the error between the commanded and achieved forces.The maximum and minimum forces by the thrusters are specified through the constraints in Eq.(6).The azimuth angles α,are required to be constrained to given sectors defined by the vectors with lower and upper bounds, αminand αmaxin Eq.(7).Moreover,the rate-of-change in azimuths is constrained in Eq.(8)and minimized by the third term in the criterion.Singularity is avoided through the last term in the criterion,where ε＞0 is required to avoid numerical problems and ρ＞0 is a weighting parameter.

The above optimization problem has been demonstrated to be effective in thrust allocation with singularity avoidance.However,the last term in Eq.(4)is very complicated and timeconsuming to be solved.

2.2 Computation effort of Johansen’s method

The computation effort of the last term for singularity avoidance is analyzed here.Assume the amount of thrusters is m,the thruster configuration matrixis a 3×m matrix.The ith column ofgiven by Eq.(2)can be represented by

where Ai,Ci,Diand Eirepresent different items inThe square matrixmatrix.The number of adding items in elements ofcan be represented by a matrix

its determinant can be represented by

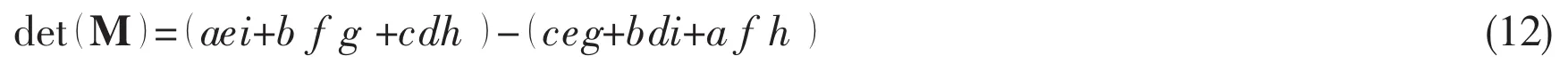
Thus,the determinant of the matrixadding terms.Suppose m=8,the termhas 11 264 adding terms.Therefore,it is really time-consuming to compute the last term in Eq.(4),since it contains the termA simple method to avoid singularity configuration is proposed in the following section.Less computation effort is expected using the simple method.

3 A simple method for singularity avoidance

In order to suppress the computation time when solving a thrust allocation problem with singularity avoidance,a simple method is presented.For a thrust system with only azimuth thrusters,the singularity configuration particularly means all thrusters has the same direction.The variance of all thrusters’angles(directions)is applied in the criterion.The variance of a set of m equally likely values can be equivalently expressed,without directly referring to the mean,in terms of squared deviations of all points from each other,see Zhang(2012)[9],

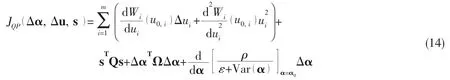
the constraints are the same as those in Johansen’s method.

Employing the simple method,the computation time of the thrust allocation problem with singularity avoidance can be expected to be dramatically suppressed.The less process time canensure the thrust allocation logic to be more efficient.

4 Time domain simulation

In order to validate the performance of the simple method,a time domain simulation for a semi-submersible with 8 azimuth thrusters was conducted.The total simulation time was 12 600 s.And the sample time was 1 s.Parameters of the semi-submersible are tabulated in Tab.1.Thruster configurations are the same as given in Fig.2.Particularities of all thrusters were the same.The maximum thrust each thruster can supply was 800 kN.The maximum change of thrust in a sample was 50 kN.The maximum change of azimuthal speed in a sample was 2°/s.

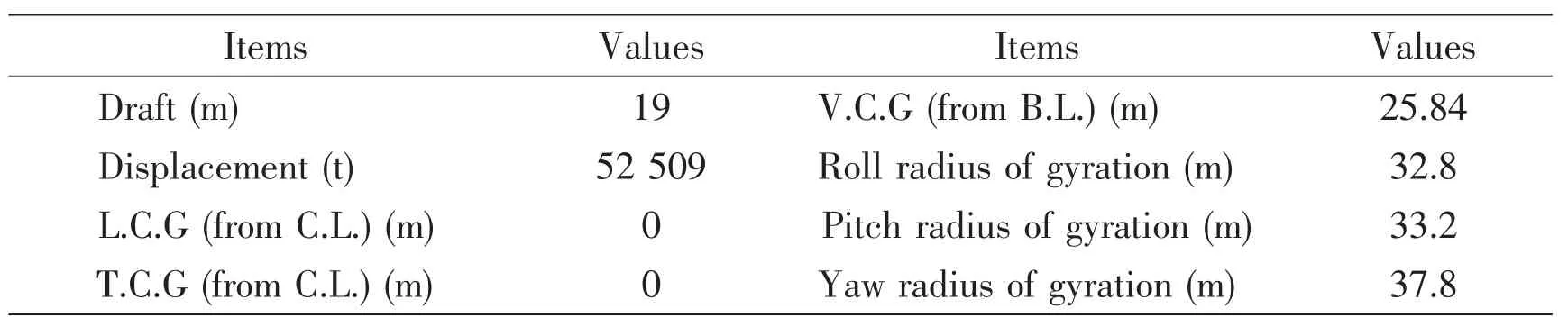
Tab.1 Parameters of the semi-submersible

The simulation was performed on a dynamic positioning time domain simulation program,DPTDSP,which was developed in SKLOE,SJTU.The structure of the program is given in Fig.3.The environmental condition and the set-position are the input.The time traces of the motion of the vessel,consumed thrust,and thruster angles can be output.The controller module computes the required forces to position the vessel based on the position error between the real-time position of the vessel and the desired position.The thrust allocation module al-locates the commanded forces among all available thrusters of the vessel.The vessel kinetics module computes the real time position of the vessel based on low-frequency motion function and wave frequency RAO,given the environmental forces and the achieved thrust forces.The observer module filters off the high-frequency and wave-frequency motions,which should not be compensated by the dynamic positioning system.

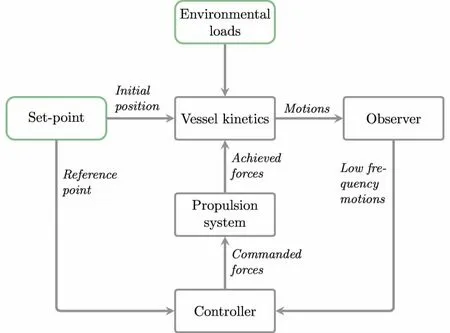
Fig.3 Structure of the DP simulator

Wind and current forces were not considered in the simulation.The irregular wave was generated based on JONSWAP spectrum with peak shape parameter 3.3,significant wave height 5.27 m,and peak period 13.4 s.Three different headings 120°,135°and 150°were considered in the simulation.

5 Results and discussions

Time traces of the motion of the vessel for 135°heading are given in Fig.4.The presented segment is taken from 1 800～2 300 s out of 0～12 600 s.The beginning 1 800 s has been excluded from the results,in order to avoid transient effect.The same rules are applied to the following presented results.

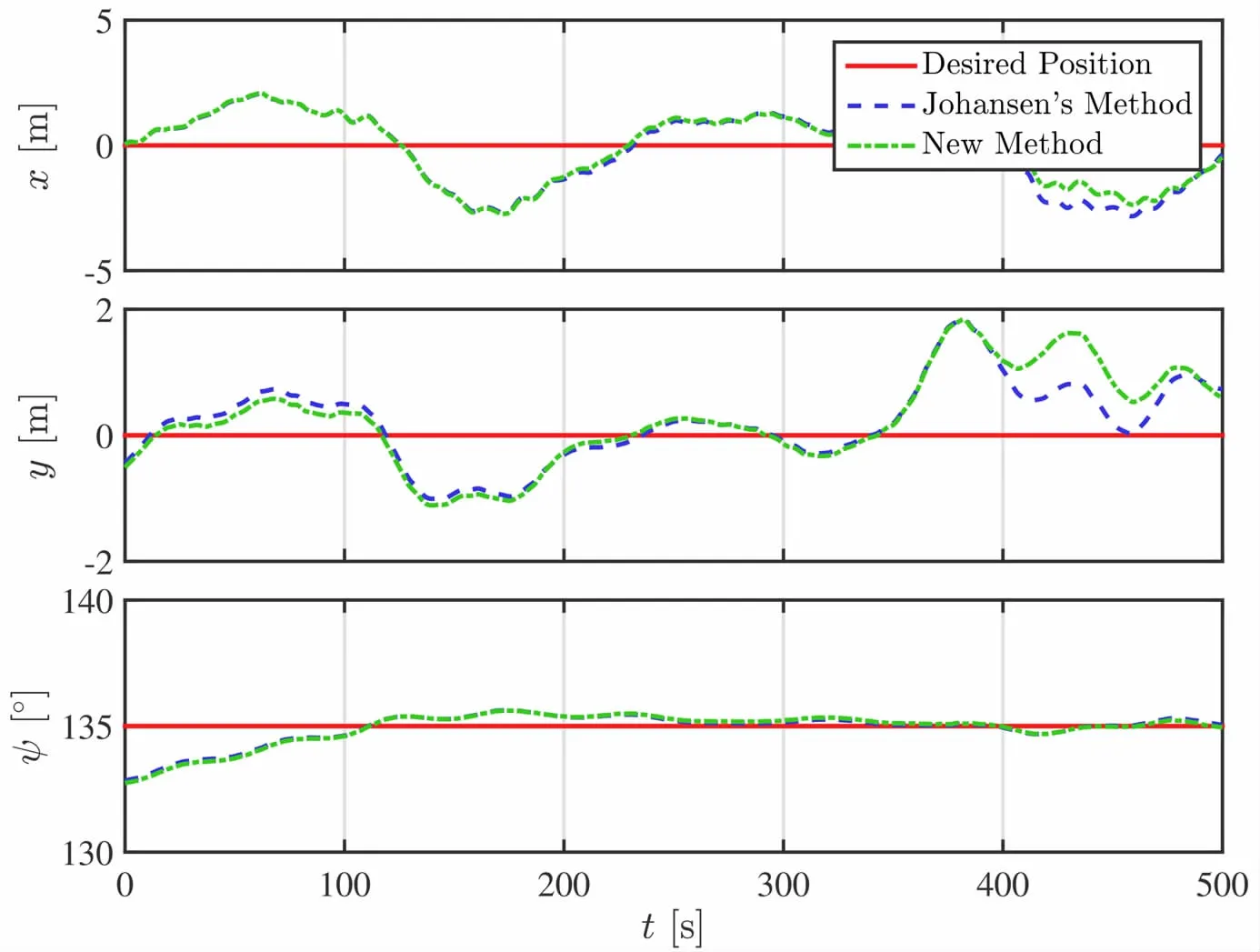
Fig.4 Time traces of the motion of the vessel for 135°heading

Time traces of the semi’s motion are almost the same when employing Johansen’s method and the simple method in thrust allocation during the simulation.The surge motion has a slightly larger deviation of the desired position using Johansen’s method than that utilizing the new method from 400～500 s.While the sway motion has a slightly smaller deviation of the desired position using Johansen’s method than that utilizing the new method in this time interval.However,the deviations are small enough to be accepted.The results also show that the mo-tion of the semi is near the desired position,especially for the yaw motion.Thus,the simple method can achieve as excellent positioning performance in DP simulation as Johansen’s method can achieve.The results of cases of the other two headings are not presented here,since they are quite similar to the results in Fig.4.

Time traces of commanded force and achieved force using two different methods in thrust allocation are presented in Figs.5-7.For 120°heading(Fig.5),the achieved forces employing the two methods in thrust allocation coincide very well with the commanded force.However,for 135°heading(Fig.6),the achieved forces employing the two methods in thrust allocation have a slight difference with the commanded force around 200 s and 400 s.The difference between the commanded force and achieved force may be one of the reason that causes motion deviations from 400～500 s in Fig.4.It can also be seen that the deviation between the achieved force and the commanded force using Johansen’s method is smaller than that using the new method,especially for the yaw moment.For 150°heading(Fig.7),similar phenomenon can be found as for 135°heading.The deviation between the achieved force and the commanded force using Johansen’s method is smaller than that using the new method,especially from 100～150 s.It can be concluded that the achieved forces using the two different methods in thrust allocation coincide very well with the commanded forces most times.And sometimes,the deviation between the achieved force and the commanded force using Johansen’s method is smaller than that using the new method.

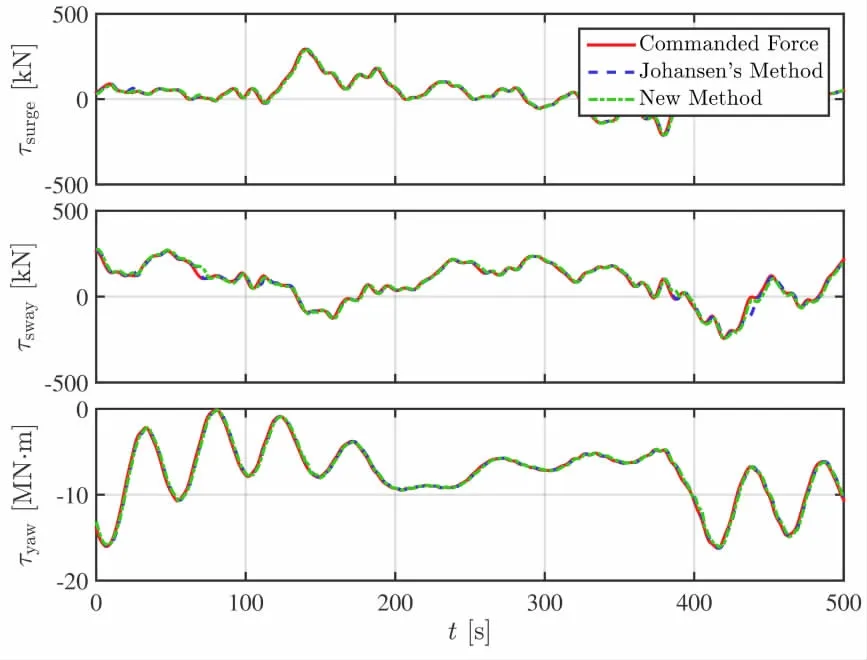
Fig.5 Time traces of commanded force and achieved force using two different methods in thrust allocation for 120°heading

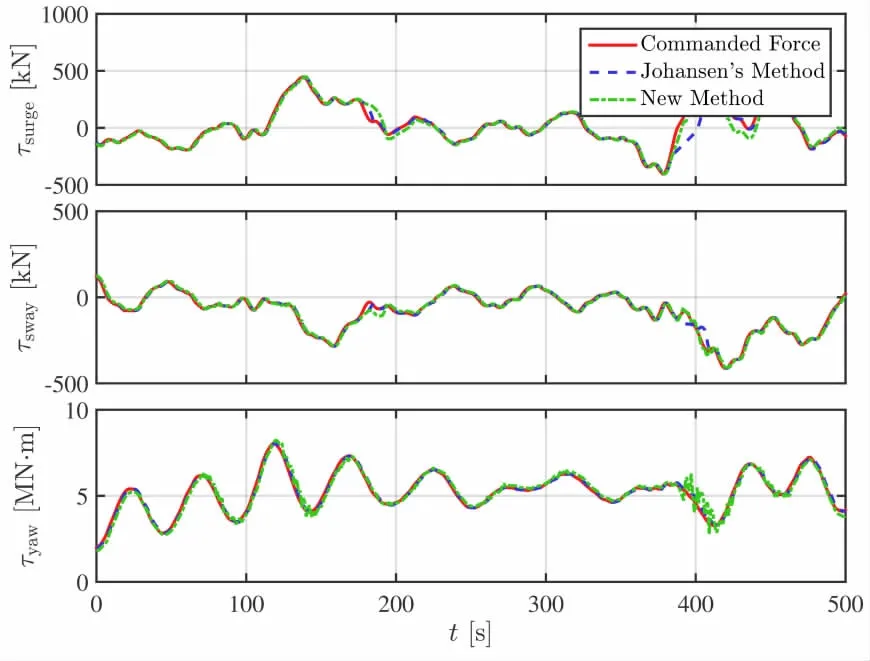
Fig.6 Time traces of commanded force and achieved force using two different methods in thrust allocation for 135°heading

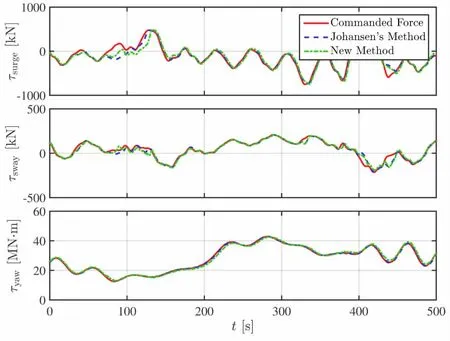
Fig.7 Time traces of commanded force and achieved force using two different methods in thrust allocation for 150°heading

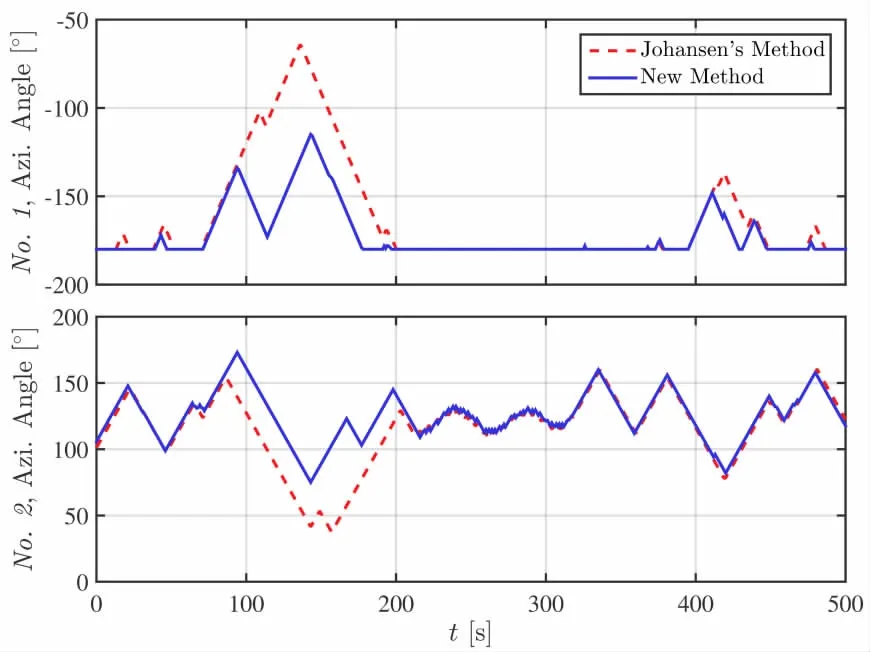
Fig.8 Time traces of the azimuth angles of thrusters No.1 and No.2 for 150°heading

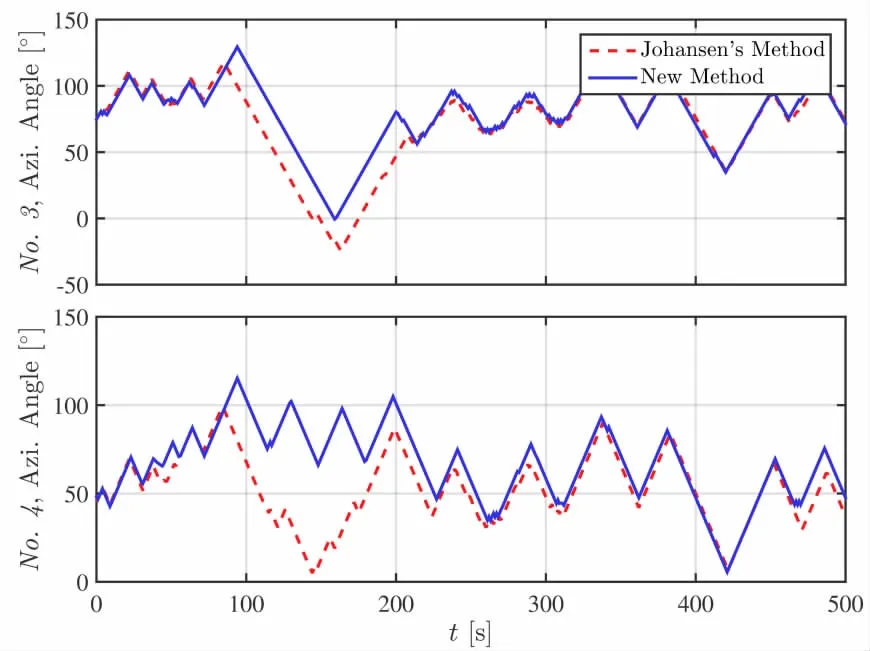
Fig.9 Time traces of the azimuth angles of thrusters No.3 and No.4 for 150°heading

Fig.10 Time traces of the azimuth angles of thrusters No.5 and No.6 for 150°heading

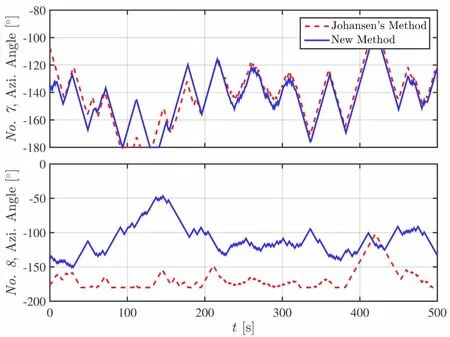
Fig.11 Time traces of the azimuth angles of thrusters No.7 and No.8 for 150°heading

Time traces of the azimuth angles of thrusters for 150°heading are presented in Figs.8-11.The results of the other two headings are quite similar to that of 150 heading.And they are not presented here for brevity.It can be seen from the results that sometimes the thrusters have the same angles while sometimes they have different angles during the simulation when the DPS employs the two different thrust allocation methods,although the two corresponding whole thrust systems supply the similar thrust forces.Moreover,no singular thruster configuration occurred during the simulation when employing the two different methods in thrust allocation.

The consumed mean and total thrust for all thrusters using the two different methods in thrust allocation during the simulation are shown in Tab.2.The statistic results were calculated from the 1 800～12 600 s out of the total simulation time 12 600 s.The consumed mean thrust of all thrusters for all cases is normal since no incredible small and large thrust is observed.This indicates that the thrust allocations with the two different singularity avoidance methods are reasonable.The total consumed thrust for all thrusters using the new method is a little(at most 4%for 150°heading)larger than that utilizing Johansen’s method.

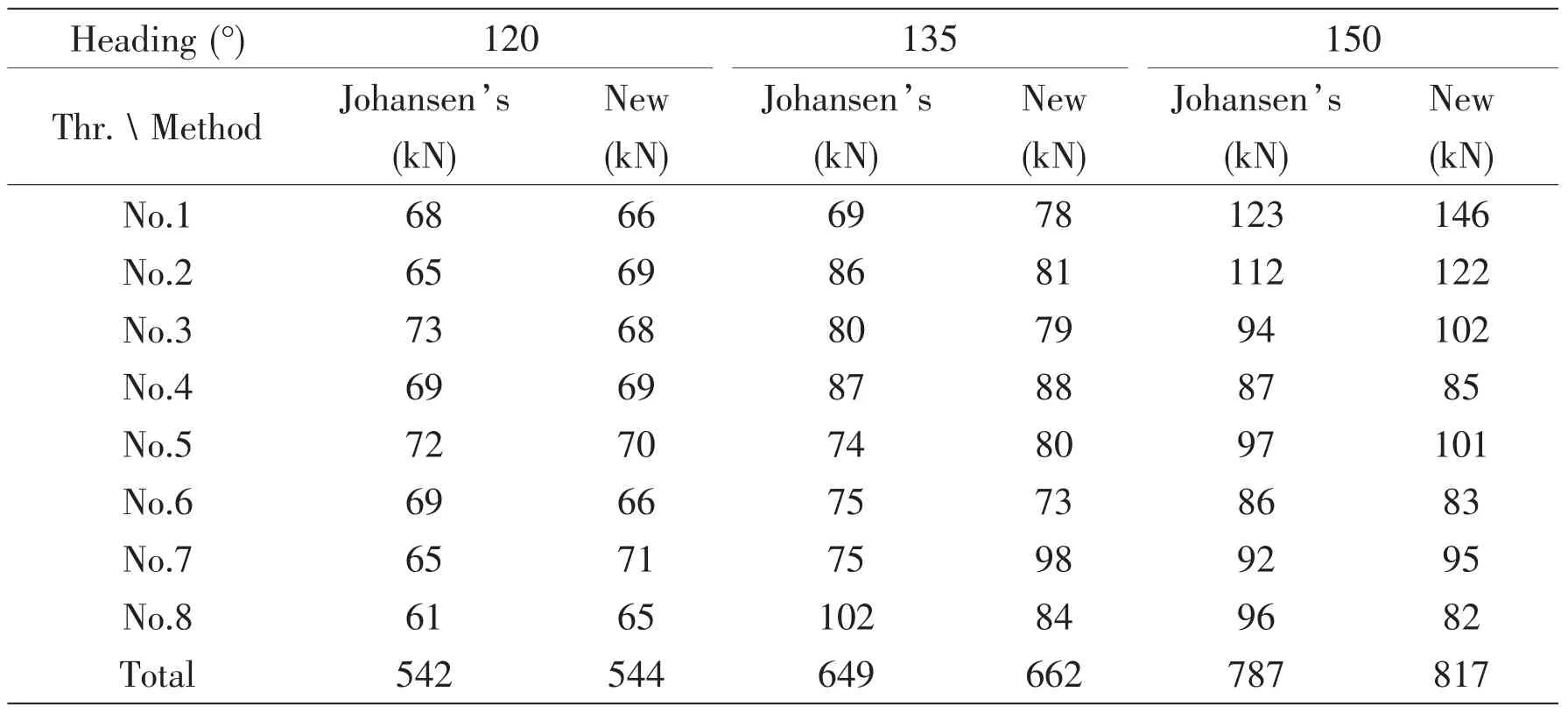
Tab.2 Consumed mean and total thrust for all thrusters using the two different methods in thrust allocation

Tab.3 Elapsed time for all cases using the two different methods in thrust allocation

The elapsed time for conducting all cases using the two different methods in thrust allocation is shown in Tab.3.tJohindicates the elapsed time employing Johansen’s method in thrust allocation for simulation.And tNewindicates the elapsed time employing the new method in thrust allocation for simulation.It is obvious that the elapsed time for simulation using the new me-thod is much(at least 12%)less than that utilizing Johansen’s method.That is the main advantage of the new method when considering singularity avoidance in thrust allocation.And it is also the main motivation of this paper.

Employing the new method in thrust allocation,the elapsed time for simulation is demonstrated to be dramatically suppressed as expected in Chap.3.The less process time can ensure the DPS to be more robust and safe,especially for a safety-critical real time system with limiting processing capability and high demands for program reliability.

6 Conclusions

In this study,a simple and new method which can avoid singular configuration in thrust allocation is proposed.The simple method is expected to be more efficient compared with existing methods.The performance of the new method was demonstrated by a time domain simulation for a semi-submersible with 8 azimuth thrusters.The simulation employed two different singularity avoidance methods including the new method and Johansen’s method.Some conclusions were drawn and summarized as follows:

(1)The simple method can achieve as excellent positioning performance in DP simulation as Johansen’s method can achieve.

(2)The achieved forces using the two different methods in thrust allocation coincide very well with the commanded forces most times.And sometimes,the deviation between the achieved force and the commanded force using Johansen’s method is slightly smaller than that using the simple method.

(3)No singular thruster configuration occurred during the simulation when employing the two different methods in thrust allocation.

(4)The thrust allocations with the two different singularity avoidance methods are reasonable.

(5)The total consumed thrust for all thrusters using the simple method is a little larger than that utilizing Johansen’s method.

(6)Employing the simple method in thrust allocation,the elapsed time for simulation is dramatically suppressed.It is the main advantage of the simple method.The less process time can ensure the DPS to be more robust and safe.

[1]Mahfouz A B,El-Tahan H W.On the use of the capability polar plots program for dynamic positioning systems for marine vessels[J].Ocean Engineering,2006,33:1070-1089.

[2]Fossen T I,Johansen T A.A survey of control allocation methods for ships and underwater vehicles,in:Control and Automation,2006[C].14th Mediterranean Conference on,IEEE,2006:1-6.

[3]Enns D.Control allocation approaches[C]//in:Proceedings of AIAA Guidance,Navigation,and Control Conference.Boston,MA,1998.

[4]Bodson M.Evaluation of optimization methods for control allocation[J].Journal of Guidance,Control,and Dynamics,2002,25:703-711.

[5]Durham W C.Constrained control allocation[J].Journal of Guidance,Control,and Dynamics,1993,16:717-725.

[6]Harkegard O.Efficient active set algorithms for solving constrained least squares problems in aircraft control allocation.in:Decision and Control[C].Proceedings of the 41st IEEE Conference on,IEEE,2002:1295-1300.

[7]Johansen Tor A,Fossen Thor I B S P.Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J].Control Systems Technology,IEEE Transactions,2004,12:211-216.

[8]Ruth E.Propulsion control and thrust allocation on marine vessels[D].Ph.D.thesis.Department of Marine Technology,Norwegian University of Science and Technology(NTNU),Trondheim,Norway,2008:203.

[9]Zhang Y,Wu H,Cheng L.Some new deformation formulas about variance and covariance,in:Modelling,Identification&Control(ICMIC)[C].Proceedings of International Conference on,IEEE,2012:987-992.

一个在船舶推力分配中避免奇异结构的简单方法

徐胜文1，2，3， 汪学锋1，2，3， 王 磊1，2，3， 李 博1，2，3， 周 利4
（1.上海交通大学 海洋工程国家重点实验室，上海200240；2.高新船舶与深海开发装备协同创新中心（船海协创中心，上海 200240；3.上海交通大学 船舶海洋与建筑工程学院，上海200240；4.江苏科技大学 船舶与海洋工程学院，江苏 镇江212003）

处在奇异结构的船舶可能会突然失位，因为无法及时提供船舶所需的推力。文章提出了一个在船舶推力分配中避免奇异结构的简单方法。为了验证这个简单方法的效果，进行了一个半潜平台的时域模拟。时域模拟中用到了两种避免奇异结构的方法，包括新提出的方法和文献中经常提到的典型方法。从结果中可以得出，这个新方法具有和典型方法同样好的推力分配效果。用这个简单方法，虽然消耗的能量有少量增加，但时域模拟所花的时间大大地缩减了。这个简单方法的高效率可以保证它在船舶动力定位的实时推力分配中得到更广的应用。

推力分配逻辑；避免奇异结构；简单方法；实时

U661.3

A

徐胜文（1986-），男，博士，上海交通大学助理研究员；汪学锋（1966-），男，上海交通大学教授；王 磊（1971-），男，上海交通大学副教授；李 博（1987-），男，博士后。周 利（1983-），男，博士，教授。

10.3969/j.issn.1007-7294.2017.09.005

Article ID： 1007-7294（2017）09-1099-15

Received date：2017-03-30

Foundation item:Supported by the Ministry of Industry and Information Technology(Mooring position technology:floating support platform engineering(II)),the National Key Research and Development Program of China(Grant No.2016YFC0303405)and the Shanghai Sailing Program(Grant No.17YF1409700)

Biography：XU Sheng-wen(1986-),male,Ph.D.,researcher fellow;WANG Xue-feng(1966-),male,Ph.D.,professor,E-mail:wangxuef@sjtu.edu.cn.