钢筋混凝土梁破坏的数值模拟
2017-10-11
(武汉船舶职业技术学院,湖北武汉 430051)
钢筋混凝土梁破坏的数值模拟
万杰
(武汉船舶职业技术学院,湖北武汉 430051)
针对钢筋混凝土梁破坏的问题,本文采用大型有限元软件ANSYS建立了4组分离式非线性有限元模型,通过数值模拟结果与理论计算结果对比发现,采用位移加载方式和不考虑压碎的SOLID65单元可以准确计算钢筋凝土简支梁的极限荷载,并且考虑SOLID65单元形函数的附加项时,可以准确模拟钢筋混凝土简支梁的破坏过程。
钢筋混凝土;破坏;模拟方法
钢筋混凝土结构是土木工程行业中应用最广泛的结构。钢筋混凝土是由钢筋和混凝土两种不同的材料组成的,充分发挥了混凝土抗压和钢筋抗拉的特性。关于钢筋混凝土结构的计算理论,目前大多数国家采用的是以概率理论为基础的极限状态设计方法,按照这一方法计算构件具有明确的可靠度指标。但极限状态设计方法基于大量的试验,而且有些试验研究具有局限性,因此准确的数值模拟方法对于大量的钢筋混凝土结构分析具有重要意义。
本文选用商业软件ANSYS进行数值模拟,ANSYS有限元软件具有功能强大的建模能力、求解能力、网格划分能力以及非线性分析能力,可进行几何非线性、材料非线性和单元非线性分析,对于钢筋混凝土的非线性行为具有良好的效果。但钢筋混凝土结构非线性程度较高、计算过程较为复杂,单元选项、本构关系、混凝土压碎的设置、网格密度、加载方式、收敛准则与精度等均对计算过程的收敛性与计算结果的准确性有很大的影响。因此本文建立了不同加载方式、混凝土压碎设置和单元选项的模型进行对比研究,得到了在满足收敛性条件下能准确模拟钢筋混凝土破坏的数值模拟方法。
1 钢筋混凝土梁模型
钢筋混凝土简支梁的尺寸为150 mm×300 mm×2 000 mm,钢筋布置形式如图1所示。混凝土采用C30混凝土,钢筋全部采用HRB335钢筋。

图1 钢筋混凝土简支梁构造图
1.1 单元选择
一般钢筋混凝土结构主要有分离式、组合式和整体式三种有限元模型,而在ANSYS软件中主要有分离式和整体式两种模型。在建模和计算时,分离式模型建模比较复杂,而且计算不容易收敛,但计算结果更加准确;而整体式模型建模比较简单,计算也容易收敛,但结果没有整体式模型精确。对于钢筋混凝土简支梁单个构件,可以采用分离式模型进行有限元分析,以便获得更为符合实际的结果,因此将混凝土与钢筋作为不同的单元来处理。混凝土采用SOLID65单元,钢筋采用LINK8单元。
1.2 材料性质
1)混凝土材料
C30混凝土立方体抗压强度标准值为30 MPa,弹性模量为3×104MPa,泊松比为0.2。当采用SOLID65单元模拟混凝土材料的开裂和压碎时,还需要输入张开裂缝的剪力传递系数C1、闭合裂缝的剪力传递系数C2、单轴抗拉强度C3,单轴抗压强度C4,双轴抗压强度C5,围压C6,围压下的双轴抗压强度C7,围压下的单轴抗压强度C8以及拉应力释放系数C9。
张开裂缝的剪力传递系数C1对计算结果影响很大,此值根据经验在钢筋混凝土简支梁中取0.5;闭合裂缝的剪力传递系数C2一般取值为0.95;单轴抗拉强度C3取C30单轴抗压强度设计值14.3 MPa;单轴抗压强度C4取单轴抗拉强度设计值1.43 MPa。在考虑混凝土压碎时C5、C6、C7、C8与C9均采用默认值。
混凝土单轴应力应变关系上升段采用《混凝土结构设计规范》(GB 50010-2002)规定的公式,下降段一般采用Hongnestad的处理方式。但混凝土本构关系一般采用ANSYS软件中多线性等向强化模型MISO模拟,由于ANSYS目前版本中多线性等向强化模型MISO无法输入下降段,因此本次研究不考虑单轴应力应变关系中下降段的影响,而采用水平线代替,如图2所示。按照(GB 50010-2002)规范规定ε0=0.002,εcu=0.003 3。

图2 混凝土的应力应变关系曲线
2)钢筋
HRB335钢筋的屈服强度为300 MPa,弹性模量为2×105MPa,泊松比为0.3,钢筋的应力应变关系采用双线性等向强化模型BISO模拟,如图3所示。

图3 钢筋的应力应变关系曲线
1.3 有限元模型
钢筋混凝土结构计算最大的问题在于正常收敛,本文为研究不同因素对计算过程收敛性与准确性的影响,建立不同有限元模型进行对比。考虑的因素包括:
(1)加载方式:力加载和位移加载。
(2)SOLID65单元的KEYOPT选项:KEYOPT(1)=0或1分别表示考虑或不考虑形函数的附加项,一般不考虑形函数的附加项容易收敛,但可能对计算结果有一定的影响。
(3)混凝土压碎的设置:当C4=-1时不考虑混凝土压碎,计算过程更容易收敛,但对计算结果的准确性未知,因此需要分别建立模型进行对比研究。
(4)收敛准则和精度:当计算过程非正常的不收敛时,将调整默认的力收敛准则和位移收敛准则为位移收敛准则,并适当放宽收敛精度。建立的有限元模型如图4所示。
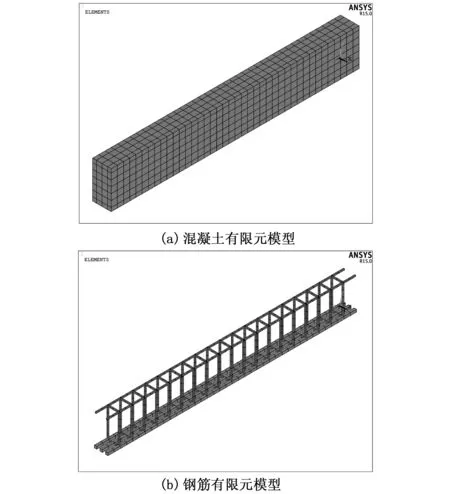
图4 有限元模型
2 计算结果及分析
2.1 力加载方式
对于力加载方式,通过在简支梁跨中施加集中荷载180 kN,然后提取跨中节点位移,得到荷载与位移曲线。
1)不考虑混凝土压碎
图5为力加载方式,不考虑混凝土压碎时KEYOPT(1)=0和1的荷载与位移曲线图。当KEYOPT(1)=0时采用位移收敛准则得到极限荷载为166.2 kN,与理论极限荷载161.54 kN误差仅为2.89%,但曲线末端不正常。当KEYOPT(1)=1时采用默认收敛准则得到极限荷载为168.1 kN,与理论极限荷载161.54 kN误差为4.1%,在达到极限荷载以后曲线缓慢上升至荷载等于180 kN。
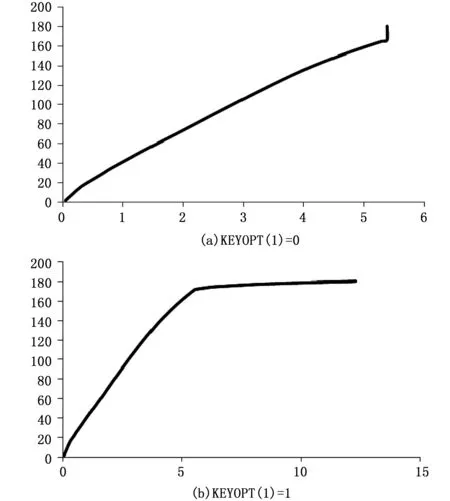
图5 荷载与位移曲线图
2)考虑混凝土压碎
图6为力加载方式,考虑混凝土压碎时KEYOPT(1)=0和1的荷载与位移曲线图。KEYOPT(1)=0和1采用位移收敛准则得到极限荷载分别为72.6 kN和109.9 kN,都与理论极限荷载161.54 kN误差很大,且曲线末端都不正常。
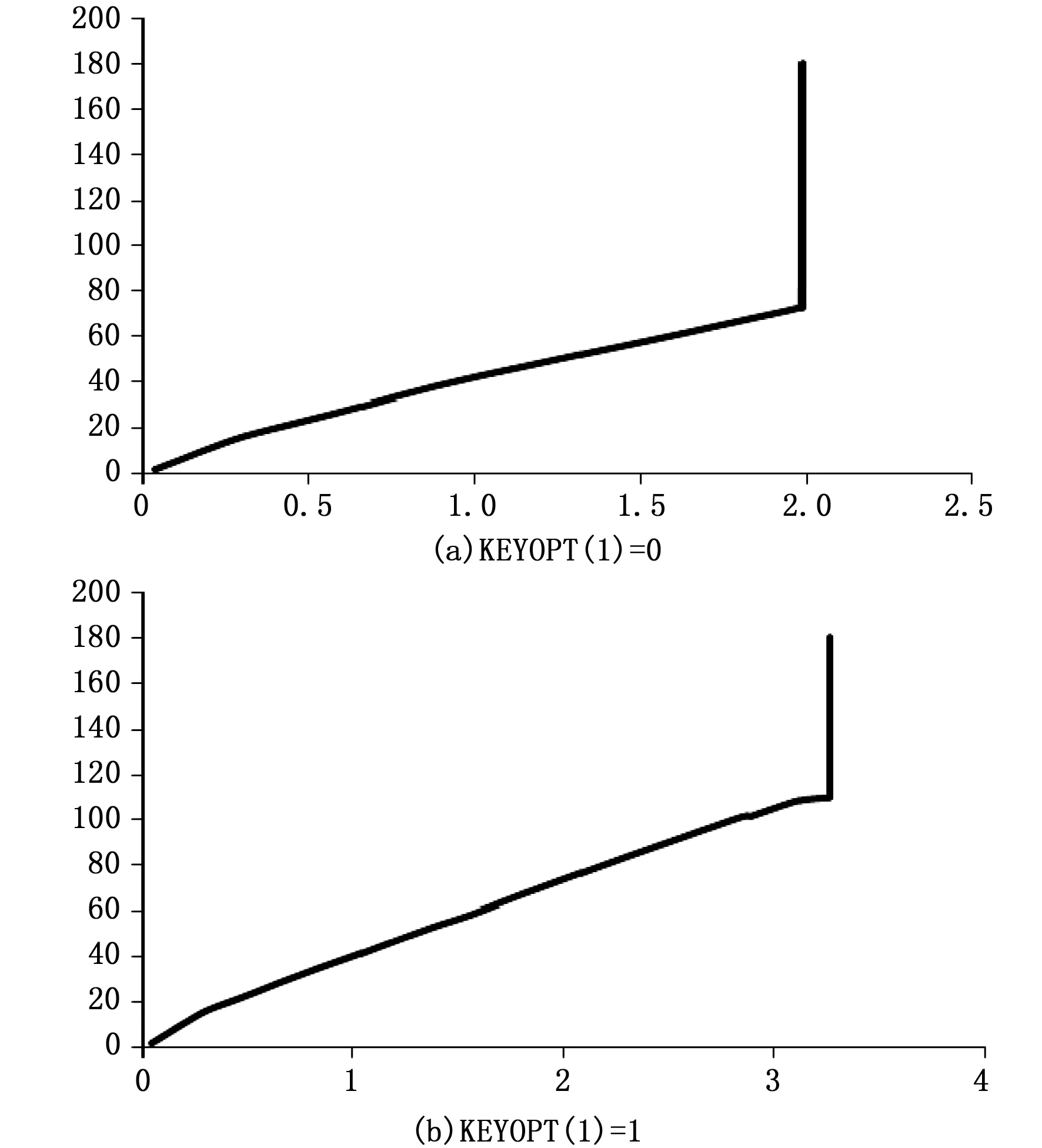
图6 荷载与位移曲线图
2.2 位移加载方式
对于位移加载方式,通过在简支梁跨中施加节点强制位移10 mm,然后提取节点支座反力,得到荷载与位移曲线。
1)不考虑混凝土压碎
图7为位移加载方式,不考虑混凝土压碎时KEYOPT(1)=0和1的荷载与位移曲线图。当KEYOPT(1)=0时采用默认收敛准则得到极限荷载为162.0 kN,与理论极限荷载161.54 kN误差为0.3%,在达到极限荷载以后曲线基本保持水平直至位移等于9.0 mm计算结束,表示构件破坏失效。当KEYOPT(1)=1时采用默认收敛准则得到极限荷载为161.67 kN,与理论极限荷载161.54 kN误差为0.1%,在达到极限荷载以后曲线缓慢上升至位移等于10 mm。
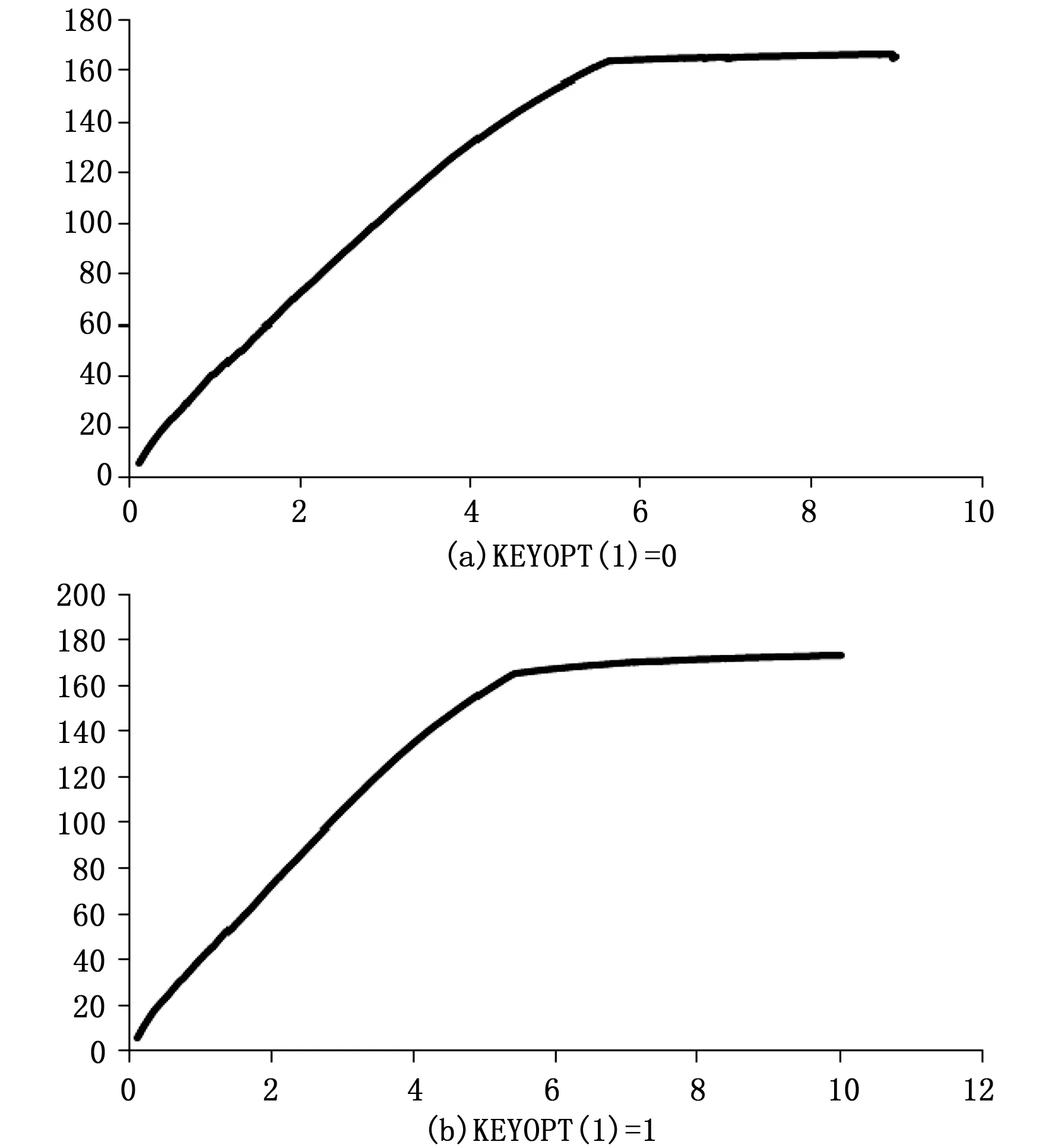
图7 荷载与位移曲线图
2)考虑混凝土压碎
图8为位移加载方式,考虑混凝土压碎时KEYOPT(1)=0和1的荷载与位移曲线图。KEYOPT(1)=0和1采用位移收敛准则得到极限荷载分别为80.2 kN和104.3 kN,都与理论极限荷载161.54 kN误差很大。

图8 荷载与位移曲线图
2.3 计算结果分析
从第二组和第四组有限元模型计算结果中可以得到,无论是力加载方式还是位移加载方式,考虑混凝土压碎后采用位移收敛准则得到的极限荷载都与理论极限荷载误差很大,曲线末端也不正常。因此模拟钢筋混凝土梁破坏过程时建议不考虑混凝土压碎。
通过对比第一组和第三组有限元计算结果可以看出,采用位移加载方式可以更为准确得到钢筋混凝土梁破坏的极限荷载。当采用位移加载方式不考虑混凝土压碎时,无论KEYOPT(1)=0或1,都能在默认收敛准则条件下准确得到极限荷载,但当KEYOPT(1)=0即考虑形函数附加项时,能从荷载与位移曲线中反映钢筋混凝土梁达到极限荷载后的破坏失效过程。因此模拟钢筋混凝土梁破坏过程时建议采用位移加载方式,并且考虑形函数附加项的影响。
3 结 语
本文通过建立不同加载方式、混凝土压碎设置和单元选项的4组钢筋混凝土简支梁有限元模型,通过数值模拟结果与理论计算结果对比得到采用位移加载方式和不考虑压碎的SOLID65单元可以准确计算钢筋凝土简支梁的极限荷载,并且考虑SOLID65单元形函数的附加项时可以准确模拟钢筋混凝土简支梁的破坏过程。
由于本文采取ANSYS程序中多线性等向强化模型MISO模拟混凝土的应力应变关系,无法考虑混凝土应力应变曲线中下降段的影响,因此应力应变曲线中下降段对模拟结果的影响有待进一步研究。
1 杨勇,郭子雄.基于ANSYS程序的钢筋混凝土梁非线性数值模拟[J].福建工程学院学报,2005, 3(6):628-632.
2 王萱. 基于ANSYS 的钢筋混凝土结构三维实体建模技术探讨[J]. 山东农业大学学报 (自然科学版),2004,35(1):113-117.
3 王新敏.ANSYS工程结构数值分析[M].北京,人民交通出版社,2007:482-485.
4 江见鲸. 钢筋混凝土结构非线性有限元分析[M].西安,陕西科学技术出版社,1994:91-128.
Abstract: In order to study the numerical simulation method of reinforced concrete beam failure, four sets of separated nonlinear finite element models are established by ANSYS software. By comparing the numerical simulation results with the theoretical results , it is found that using displacement loading method and SOLID65 element without consideration of crushing can accurately calculate the ultimate load of reinforced concrete simply supported beam, and consider the additional function of SOLID65 element shape function can accurately simulate the failure process of reinforced concrete simply supported beam. This research provides an effective simulation method for the failure of reinforced concrete structures.
Keywords:reinforced concrete;failure; simulation method
(责任编辑:谭银元)
ResearchontheNumericalSimulationforReinforcedConcreteBeamFailure
WANJie
(Wuhan Institute of Shipbuilding Technology, Wuhan 430051,China)
TU52
A
1671-8100(2017)03-0043-05
2017-04-11
万 杰,主要从事工民建方面的教学和科研工作。
