95°～135°不规则Z形弯管应力变化规律

2017-10-11平飞王飞王国伟雷勇刚

华侨大学学报（自然科学版） 2017年5期

关键词：管径曲率转角

平飞，王飞，王国伟，雷勇刚

(太原理工大学环境科学与工程学院，山西太原 030024)

95°～135°不规则Z形弯管应力变化规律

平飞，王飞，王国伟，雷勇刚

(太原理工大学环境科学与工程学院，山西太原 030024)

假设管道材料为无限弹性体，采用ANSYS有限元分析软件，对95°～135°范围内不规则Z形直埋供热弯管进行数值模拟,并绘制各种参数下弯管最大应力变化曲线图和DN1 200不规则Z形弯管在95°～135°转角下的线算图.模拟结果表明：随着膨胀垫厚度、壁厚、管径的增加，弯管应力最大值逐渐减小；随着补偿弯臂、曲率半径的增加，弯管应力最大值先减小后增大；DN1 200不规则Z形弯管的补偿能力随着转角角度的增加而削弱.

直埋供热； Z形弯管；补偿弯臂；弯管应力；数值模拟

Abstract： The pipeline was assumed to be an infinite elastic solid, and the ANSYS software for finite element analysis was applied to conduct numerical simulation analyzing the irregular Z-shaped directly-buried heating elbow which was between 95° and 135°. The graph was drawn to describe the change of maximum stress on elbow with the various parameters, and the alignment chart was drawn to describe the DN1 200 irregular Z-shaped elbow with a curvature of 95°-135°. The simulation results showed that, the increase of the thickness of expansion cushion, thickness of pipe wall and pipe size will lead to a decreasing of the maximum stress on elbow; along with the compensation bent arm and radius of curvature increasing, the maximum stress on elbow first decreases then increases; and the increase of the elbow angle will give rise to weaken the compensation ability of the DN1 200 irregular Z-shaped elbow.

Keywords： directly-buried heating; Z-shaped elbow; compensation bent arm; elbow stress; numerical simulation

目前,城市集中供热设计温度已达150 ℃，设计压力达2.5 MPa，管径也达到1 400 mm[1].管道敷设过程中，由于规划路由和施工场地条件的约束，不规则Z,L和Π形直埋弯管被大量使用.然而，CJJ/T 81-2013《城镇供热直埋热水管道技术规程》(以下简称《规程》)中仅规定了针对转角角度为90°的Z形补偿管段的计算方法和使用依据[2]，并没有与其相关的技术应用标准.自上世纪70年代以来，学者们针对90°弯头强度进行研究，给出了弯头强度计算的解析方法[3-5].李明强等[6],姚红等[7]通过对规则Z形补偿弯管的数值分析，解决了补偿弯臂直管段在0～2倍弯头变形段长度变化过程中，其应力变化规律及弯管应力计算模型的问题.从目前的研究看，对不规则Z形直埋弯管的研究鲜有报道.工程中,盲目地增设补偿器和固定墩等附件对弯管进行保护，一方面，增加了工程投资，另一方面，也增加了供热直埋管道的事故危险点，降低管网的可靠性.因此，本文采用ANSYS有限元分析软件，分别在补偿弯臂长度、管道壁厚、膨胀垫厚度、管径、曲率半径等结构尺寸变化条件下，对95°～135°范围内的不规则Z形直埋供热弯管应力大小和最大允许被补偿臂长进行模拟分析.

1 管道应力的数学模型

将单元体位移、应变及应力利用节点的位移表征.首先，针对于连续体分析时，应对单元中唯一的分布给出相应的假设，即将位移假设为坐标的某种简单函数，并将这种简单函数称作位移函数(形函数)，表达式为

式(1)中：u为单元内任意一点的位移列阵；N为形函数列阵；δe为单元节点位移列阵.

其次，根据几何方程，将单元应变的关系式通过位移表达式进行表达，利用节点的位移表征,即

式(2)中：ε为单元内任意一点的应变列阵；B为应变矩阵.

再根据物理方程，将单元应力的关系式通过应变表达式进行表达，利用节点的位移表征,即

式(3)中：σ为单元内任意一点的应力列阵；D为单元材料有关的弹性矩阵.

根据虚功原理建立刚度方程(平衡方程)，即作用在单元上节点力和节点位移二者之间的关系式为

式(4)中：Ke为单元刚度阵；Re为单元上的节点力列阵.

最后,计算相邻单元边界的等效节点力，针对整个结构建立刚度方程进行有限元计算，即将所有单元的刚度方程集合，求解节点的位移及计算单元应力.

2 水平对称不规则Z形补偿弯管的数值模拟

2.1物理参数

不规则Z形直埋供热弯管,如图1所示.图1中:L1为补偿弯臂长度；L2为补偿弯臂直管段长度；L3和L4为被补偿臂长度；φ为转角角度；Rc为弯头曲率半径.

图1 不规则Z形直埋供热弯管Fig.1 Irregular Z-shaped directly-buried heating elbow

管道材料选用Q235B，并假设为理想的弹塑性材料，杨氏弹性模量E=198 GPa；线膨胀系数α=12.4 μm·(m·℃)-1；泊松比υ=0.3；工作压力Pn=2.5 MPa；循环最高温度θ1=130 ℃；循环最低温度θ2=10 ℃；循环温差ΔT=120 ℃；土壤摩擦系数为0.2[5]；管顶埋深h=1.5 m.

2.2几何参数

管道基本数据[8],如表1所示.表1中：D0为外径；Di为内径；Dc为保温管外径；Le为弯头变形段长度,计算式[5]为

表1 管道基本数据表Tab.1 Basic data table of pipeline m

式中：k为与土壤特性和管道刚度有关的参数，m-1；C为土壤横向压缩反力系数，N·m-3；E为钢材的弹性模量，MPa；Ip为直管工作管横截面的惯性矩，m4.

2.3模型简介

综合基床系数根据文献[9]的方法进行计算.在总结文献[6-7]研究成果的基础上，通过增加模型表面效应单元STRUCTURAL154模拟管土之间摩擦力的作用，解决应力值偏大的问题[10].根据文献[7]中表5提供的模拟条件，得到改进后的模拟值，结果如表2所示.表2中：L1为补偿臂长.

表2 模型改进前后弯管应力最大值比较Tab.2 Comparison of maximum stress on elbow of model before and after improvement

文中被补偿臂长度取L3=L4=50 m，网格间距0.05 m.由于管道与土壤的耦合作用，需要每个管道模型节点与土弹簧单元节点一一对应，因此，体网格划分采用体扫略的方式.荷载和边界条件的施加参见文献[6-7].

3 结果与分析

表3为模拟工况.表3中：δ为弯头壁厚；s为膨胀垫厚度.选择模拟转角角度在95°～135°变化范围内，按照表3所列的变量和工况，分析各变量对不规则Z形直埋供热弯管最大应力的影响.

表3 模拟工况Tab.3 Simulated conditions

在研究最大允许被补偿臂长随转角角度的变化时，模拟工况为Pn=2.5 MPa，h=1.5 m，ΔT=120 ℃，管径DN1 200，δ=14 mm，L1=1.5Le，Rc=6.0DN，s=40 mm.其最大应力值位于弯头中性面与对称截面相交位置处，如图2所示.

图2 不规则Z形直埋供热弯管应力云图Fig.2 Stress nephogram of irregular Z-shaped directly-buried heating elbow

3.1补偿弯臂长度对弯管应力大小的影响

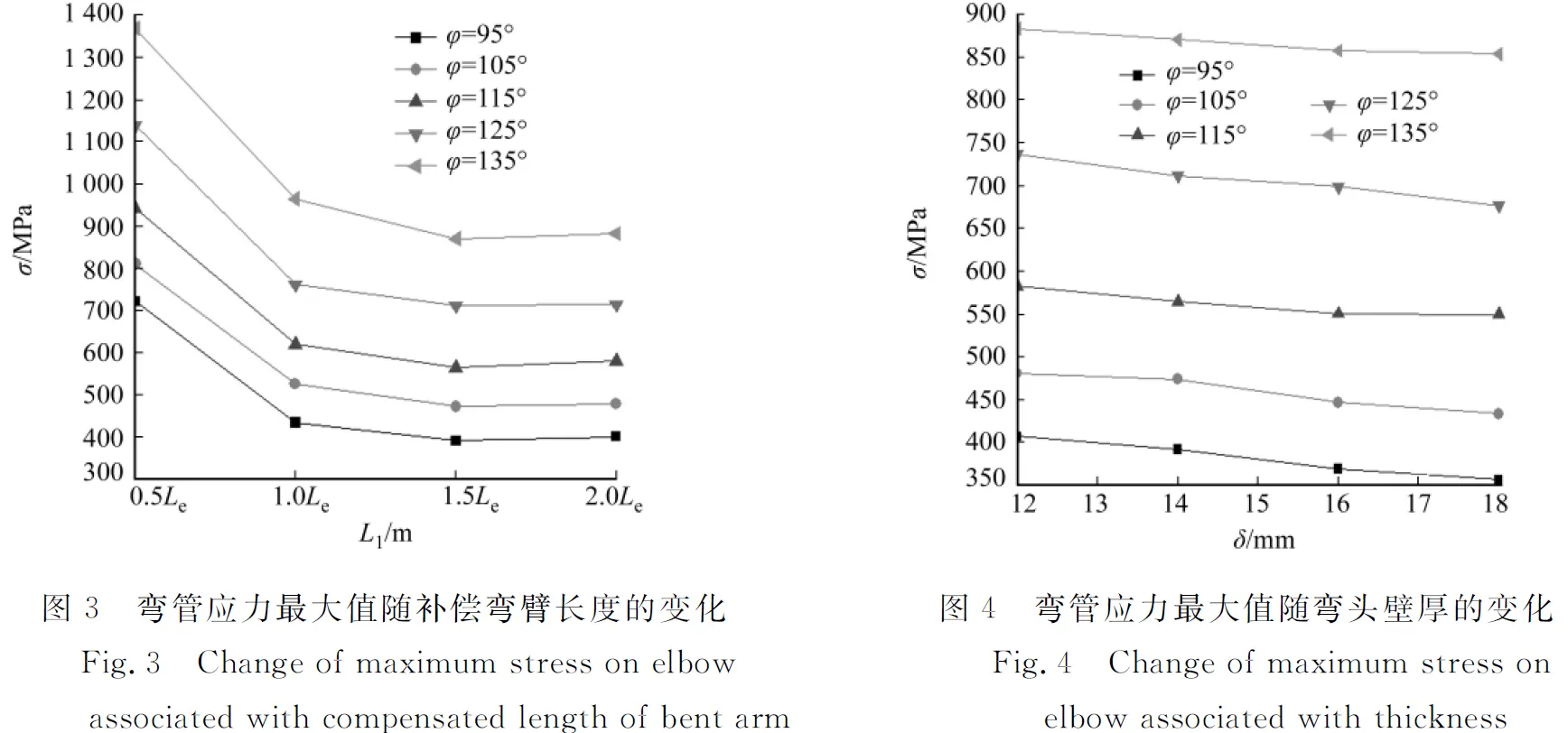
弯管应力最大值(σ)随补偿弯臂长度(L1)的变化规律,如图3所示.由图3可知：对于95°～135°范围内的不规则Z形直埋供热弯管，随着补偿弯臂L1的增加，弯管应力最大值逐渐减小.这是由于在不规则Z形直埋供热弯管中，某侧弯臂的轴向热膨胀是通过另一侧弯臂的横向位移吸收的，如果补偿弯臂过短，无法保证补偿弯臂产生足够的横向位移，不具备良好的侧向变形能力，导致弯管应力增大，最终使弯管应力最大值增大.但是，在由L1=1.5Le增加到L1=2.0Le的过程中，补偿弯臂向弯头处释放的热膨胀量增大，导致弯管最大应力值略有增加.当转角角度分别为95°，115°，135°时，补偿臂长从1.5Le增加到2.0Le的过程中，其应力最大值分别增加了2.56%，2.83%，1.38%.

由此可见，在一定范围内，增加补偿弯臂长度能提高弯管补偿能力，但如果单纯增加L1，会导致弯管最大应力值不降反增.在同一补偿弯臂长度的条件下，随着转角角度的增加，弯管应力最大值显著增大，说明不规则Z形直埋供热弯管随转角角度的增加，补偿能力下降.

3.2弯头壁厚对弯管应力大小的影响

弯管应力最大值(σ)随弯头壁厚(δ)的变化规律，如图4所示.由图4可知：对于95°～135°范围内的不规则Z形直埋供热弯管，随着弯头壁厚的增加，弯管应力最大值逐渐减小，且这种影响随着转角角度的增大而逐渐减弱，这种变化趋势与文献[11]阐述的相同.究其原因，在其他模拟工况一定时，随着弯头壁厚的增大，弯头断面的抗弯矩增大，而弯管的应力加强系数减小，导致弯管应力减小，最终使弯头处应力最大值减小.当转角角度分别为95°，115°，135° 时，壁厚δ从12 mm增加18 mm的过程中，其应力最大值分别减小了50，33，30 MPa.说明对于较大转角的不规则Z形直埋供热弯管，增加壁厚对于减小弯管的最大应力效果不大.在同一壁厚的条件下，随着转角角度的增加，弯管应力最大值显著增大，说明不规则Z形直埋供热弯管随转角角度的增加，补偿能力下降.

3.3弯头处膨胀垫厚度对弯管应力大小的影响

弯管应力最大值(σ)随弯头处膨胀垫厚度(s)的变化规律，如图5所示.由图5可知：对于95°～135°范围内的不规则Z形直埋供热弯管，随着膨胀垫厚度的增加，弯管应力最大值逐渐减小，且随着转角角度的增加，弯管应力最大值减小的幅度逐渐增大.这是由于在弯头两侧放置膨胀垫块，随着膨胀垫厚度的增加，综合基床系数越小，即土壤对弯管的压缩反力减小，导致弯管的应力减小，最终使弯头处应力最大值减小.当膨胀垫厚度从0 mm增加到120 mm的过程中，φ=95°时的弯管应力最大值减小了44 MPa；φ=115°时的弯管应力最大值减小了71 MPa；φ=135°时的弯管应力最大值减小了108 MPa.说明转角角度越大，增加膨胀垫厚度对降低弯管最大应力越有效.在同一膨胀垫厚度的条件下，随着转角角度的增加，弯管应力最大值显著增大.

3.4管径对弯管应力大小的影响

弯管应力最大值(σ)随管径(DN)的变化规律，如图6所示.由图6可知：对于95°～135°范围内的不规则Z形直埋供热弯管，随着管径的增大，弯管应力最大值逐渐减小，这种变化规律与文献[11]阐述的相同.究其原因，当其他模拟工况一定时，随着管径的增大，弯管的应力加强系数及弯头断面的抗弯矩均增大，但抗弯矩增加速度较应力加强系数的增加变化快，导致弯管应力减小，最终使弯头处应力最大值减小.当φ=105°时，管径DN800,DN1 000,DN1 200的应力最大值分别为574，535，481 MPa.

可以发现，增大管径可以有效地减少弯管的应力最大值.因此，对大口径不规则Z形直埋供热弯管的应用，应充分发挥其补偿能力.在同一管径条件下，随着转角角度的增加，弯管应力最大值显著增大.

3.5弯头曲率半径对弯管应力大小的影响

弯管应力最大值(σ)随曲率半径(Rc)的变化规律，如图7所示.由图7可知：对于95°～135°范围内的不规则Z形直埋供热弯管，不同转角角度均在Rc=6.0DN处出现拐点，当Rc<6.0DN时，弯管应力最大值随着曲率半径的增大而显著减小；当Rc>6.0DN时，弯管应力值随着曲率半径的增大逐步增大.当转角角度分别为115°，125°，135° 时，曲率半径从Rc=1.5DN增加到Rc=6.0DN，其应力最大值分别减小了35.75%，39.47%，39.38%；当曲率半径从6.0DN增加到15.0DN时，其应力最大值分别增大了33.88%，20.19%，8.71%.

由此可得，在Rc=6.0DN范围内，增加曲率半径可以提高弯管的补偿能力.这是由于在其他模拟工况一定时，随着曲率半径在6.0DN范围内增大，弯管的尺寸系数增大，导致弯管的应力加强系数减小，弯矩作用条件下的弯管应力减小，最终使弯管应力最大值减小.但如果超过Rc=6.0DN，弯管最大应力不降反增，即对于不规则Z形直埋供热弯管，当补偿臂长L1保持不变，弯管曲率半径无限增大的同时，等量缩短直臂L2来增加弯头的承载能力没有任何意义.在同一曲率半径的条件下，随着转角角度的增加，弯管应力最大值显著增大.

3.6弯管最大允许被补偿臂长随转角角度的变化

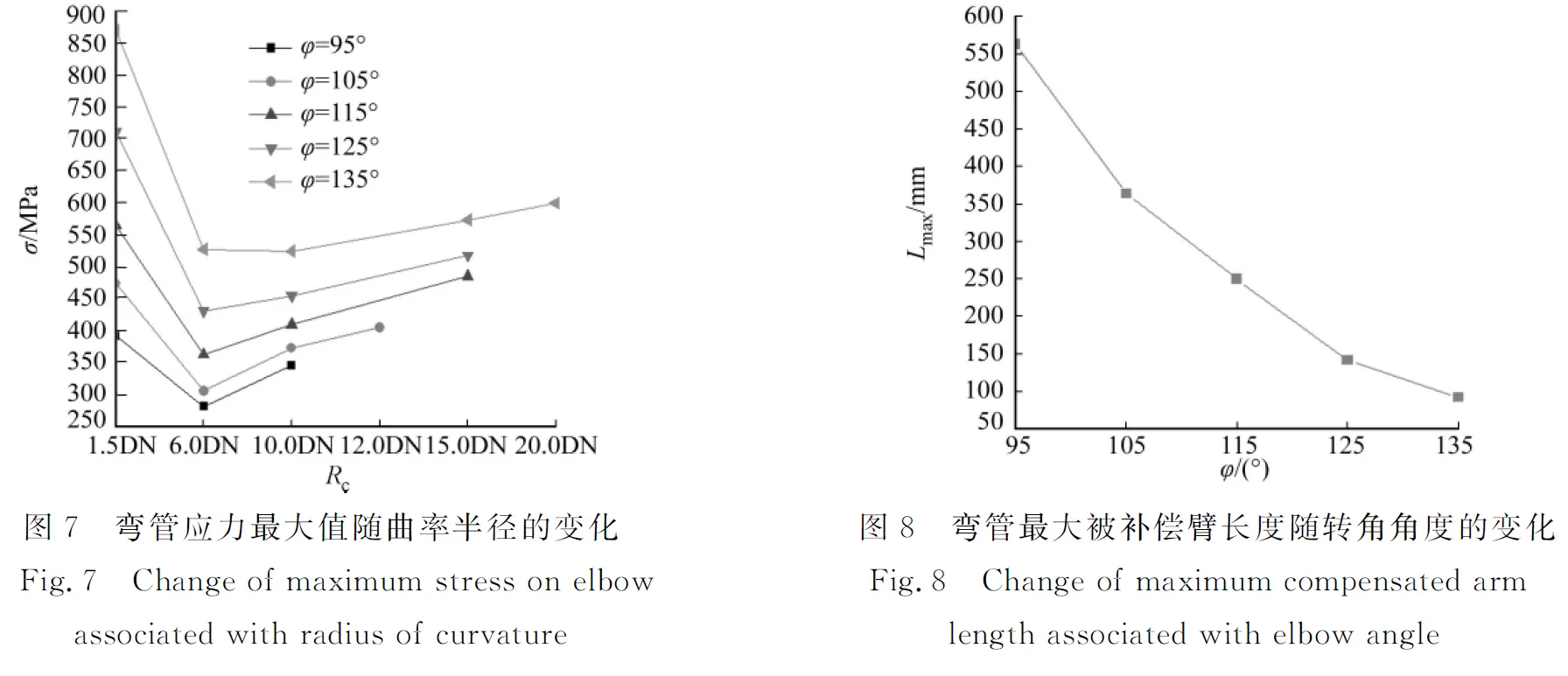
选择管径为DN1 200时，弯管最大被补偿臂长度(Lmax)随转角角度(φ)的变化，如图8所示.由图8可知：管径为DN1 200的不规则Z形直埋供热弯管，随着转角角度的增加，最大允许被补偿臂长呈显著减小的趋势.究其原因，当其他模拟条件一定时，随着转角角度的增加，弯头处产生较大应力，能够吸收热膨胀变形的能力逐渐减弱，最终导致弯管的补偿能力下降.当转角角度分别为95°，115°，135°时，管径DN1 200的最大允许被补偿臂长度分别为563，250，93 m，依次分别减少了55.60%和83.48%.由此可得，随着转角角度的不断增大，不规则Z形直埋供弯管补偿能力逐渐下降.