采用自适应模糊PID控制的多级齿轮振动主动控制
2017-10-11张锋李海燕汪涵孙文豪罗顺安
张锋, 李海燕, 汪涵, 孙文豪, 罗顺安
(华侨大学 机电及自动化学院, 福建 厦门 361021)

采用自适应模糊PID控制的多级齿轮振动主动控制
张锋, 李海燕, 汪涵, 孙文豪, 罗顺安
(华侨大学 机电及自动化学院, 福建 厦门 361021)
针对齿轮传动系统在动态激励的作用下产生的多谐波复杂振动,设计一种在低速轴和高速轴分别安装有压电促动器的主动控制结构;提出一种将传统PID控制和自适应算法相结合的自适应模糊PID算法,抑制能量较高的多个谐波振动.在ADAMS平台建立齿轮传动系统虚拟样机,作为被控对象子模块,并在MATLAB/Simulink平台上加载控制算法对系统进行联合仿真.仿真结果表明:在不同转速下,自适应模糊PID控制算法对谐波振动具有良好的控制效果,且优于经典PID控制.
齿轮传动系统; 振动主动控制;自适应模糊PID控制;控制逻辑;谐波振动
Abstract: Aiming at controlling multi-harmonic complex vibration generated by dynamic excitation of gear transmission system, an active control structure with piezoelectric actuators mounted on low-speed shaft and high-speed shaft was designed. A controller which was based on the fuzzy adaptive PID algorithm combined with traditional PID control and adaptive algorithm was proposed to suppress the energy of multiple harmonic vibrations. The virtual prototype of the gear transmission system was established as a controlled object on the ADAMS platform, and the system was simulated by loading the control algorithm on the MATLAB/Simulink platform. The simulation results show that the adaptive fuzzy PID control algorithm has a good control effect on the harmonic vibration at different rotational speeds, and it achieves better control performance than the classical PID control algorithm.
Keywords: gear transmission system; active vibration control; adaptive fuzzy PID control; control logic; harmonic vibration
随着航空、航天、机器人等领域的不断发展,对于齿轮精度、齿轮振动与噪声的要求也越加苛刻.降低齿轮振动[1-2]可以改善工作环境,显著地提高机械装备的工作寿命和可靠性.齿轮传动为非线性时变系统,单靠被动控制无法解决齿轮系统的振动问题,需加入主动控制算法才能更有效地限制齿轮系统的振动.齿轮传动系统的内部激励是具有周期性的,产生的振动能量主要集中在齿轮啮合频率及其谐波频率处,因此,降低主要频率处的振动就能抑制齿轮系统整体的振动,国内外已有学者对此展开研究.Guan等[3]提出采用单只压电促动器构建齿轮主动控制结构,利用促动器的主动控制力来抑制齿轮的啮合振动.Belanger等[4]建立了一个直升机传动系统的有限元模型,利用压电促动器来控制齿轮箱的振动传播.李以农等[5]利用FxLMS算法对齿轮系统进行主动控制.范振华[6]设计了单级齿轮传动系统,搭建振动主动控制平台,并采用PID控制和模糊控制作为控制器核心.以上研究主要是围绕单级齿轮传动的主动控制进行的.多级齿轮的振动耦合更为复杂,除了单轴模态和轴间耦合模态外,还派生出新的模态,使得振型分布较密,振动频率成分复杂.本文在齿轮系统的输入轴和输出轴上各安装压电促动器,提出一种自适应模糊PID(adaptive fuzzy PID,AFPID)控制策略来抑制箱体的振动,并验证这种主动控制对于抑制齿轮传动过程中的径向振动的有效性.
1 多级齿轮传动机构的主动控制结构建模
齿轮加工误差、齿轮刚度的时变性、外载荷的变化,以及啮合冲击等因素都会产生影响齿轮传动的啮合激励[7].在激励源附近添加一个控制力,可以有效地降低啮合激励.文中设计一种内置压电促动器的齿轮传动主动控制结构,如图1所示.图1中:调速驱动电机满足速度大范围可调、速度波动较小的要求;测功机包括磁粉制动器和转矩传感器两部分构成;压电促动器是一个利用压电陶瓷的逆压电效应,通过施加外部电场,将电能转化为机械能的装置[8].图2为主动控制机构内部的放大图.图2中:压电促动器支撑机构由促动器支架、防载棒和支撑轴承构成.促动器支架固定于箱体内部,促动器的尾端固定在促动器支架上以限制其移动,前端与齿轮轴的衔接处添加一支撑轴承,针对齿轮轴的径向振动输出控制力,从而衰减齿轮轴的弯曲振动.通过传动系统的设计与校核,得到各级齿轮的基本数据,如表1所示.


表1 各级减速器齿轮参数Tab.1 Reducer gear parameters at all levels
2 自适应模糊PID的控制原理
PID控制的核心是对PID控制器的3个参数进行整定,使其输出达到最优,使控制达到所期望的控制效果.但随着控制系统被控对象的复杂化,很多时候被控对象的精确模型无法建立,PID控制的3个参数无法保持最优解的状态[9].将模糊控制[10]与传统PID控制算法相结合,形成模糊PID(FPID)复合控制,可以弥补模糊控制器消除稳态误差较差的缺点.但FPID由于积分控制和微分控制的相互影响,控制规则不易设计,对专家经验的依赖较大.
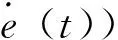

图3 AFPID控制器原理图Fig.3 AFPID controller schematic
由此可得,控制器的输出为

AFPID算法可分为PI型、PD型和PID型.PI型模糊控制器的控制过渡过程较差,PD型模糊控制器产生输出存在稳态误差,相比之下,PID型自适应模糊控制器具有更好的控制效果.
3 自适应模糊PID控制器的设计
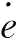
3.1模糊化
总而言之,将3.0T MRI应用在生长激素缺乏矮小儿童垂体病变中,可较为准确地显示出各种垂体病变的特点,提高诊断的准确率,临床应用价值较高。
3.2建立模糊控制规则
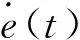
表2 ΔKP的模糊规则表
Tab.2 Fuzzy rules table for ΔKP

JZ(〛EECNBNSZOPSPBNBPBPBPBPSZONSPBPSPSZONBZOPSPSZONSNBPSPSZONSNSNBPBZONSNSNBNB
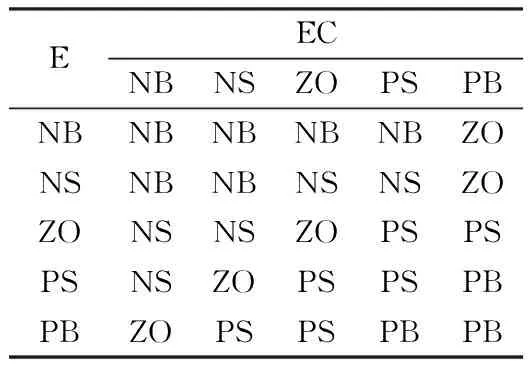
表3 ΔKI的模糊规则表Tab.3 Fuzzy rules table for ΔKI
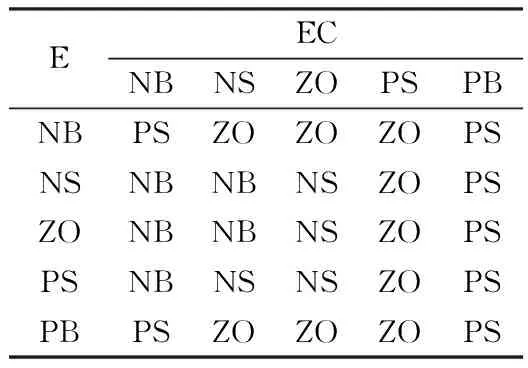
表4 ΔKD的模糊规则表Tab.4 Fuzzy rules table for ΔKD
3.3清晰化
模糊规则推理的结果是一个模糊集,不能直接用来作为被控对象的控制量,需要把它变成可以执行的精确量,这个过程被称为清晰化[13].清晰化的目的是根据模糊推理的结果,得到最能反映控制量的实际分布.文中采用具有直观合理和计算方便的最大隶属度法来进行这个过程.
4 虚拟样机的建立
在ADAMS软件中,碰撞力的定义为
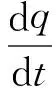
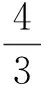
两对齿轮材料均取45钢,其泊松比v1=v2=0.27,杨氏模量E1=E2=0.207 TPa,结合表1数据,经计算,高速级齿轮碰撞刚度系数K高=0.527 MN·mm-3/2;低速级齿轮碰撞刚度系数K低=0.554 MN·mm-3/2.在撞击过程中力的变化主要是由弹簧控制,由于阻尼器所吸收的能量是撞击总能量很小的一部分,因此,阻尼系数C一般取得较小[14-16],C=50,碰撞指数e=1.5,渗透深度d=0.1 mm.动摩擦系数为0.05,静摩擦系数为0.08.为使启动时转速不发生突变,采用STEP函数使转速在0.1 s内提升到2 500 r·min-1,STEP(time,0,0°,0.1,15 000°),输出轴上增加一个负载转矩为1.0 kN·mm.
将齿轮轴进行柔性化处理,ADAMS平台中的柔性轴处理与有限元不同,是把一根刚性轴分离成若干柔性相连的短刚性轴,创建出柔性连接件,其实质仍是刚体.
5 ADAMS/MATLAB联合仿真
在ADAMS平台中针对建成的多级齿轮传动系统模型各部件之间的关系,添加相应约束,最终得到齿轮传动系统虚拟样机.ADAMS和MATLAB的联合仿真是在ADAMS中建立齿轮传动虚拟样机模型,输出成为具备系统方程与相关参数的模块,在MATLAB中将模块中的数据与建立的控制方案结合起来,由ADAMS求解系统方程,MATLAB求解控制方程,共同完成整个仿真过程.
为验证多级齿轮传动的AFPID控制的可行性,采用MATLAB/Simulink进行仿真,观察齿轮传动系统控制前后的现象.分析AFPID控制针对齿轮啮合频率和谐波频率处振动的控制效果,并且与经典PID控制进行对比,如图4,5所示.

图4 基于AFPID控制的主动控制联合仿真Fig.4 Active simulation of active control based on AFPID control
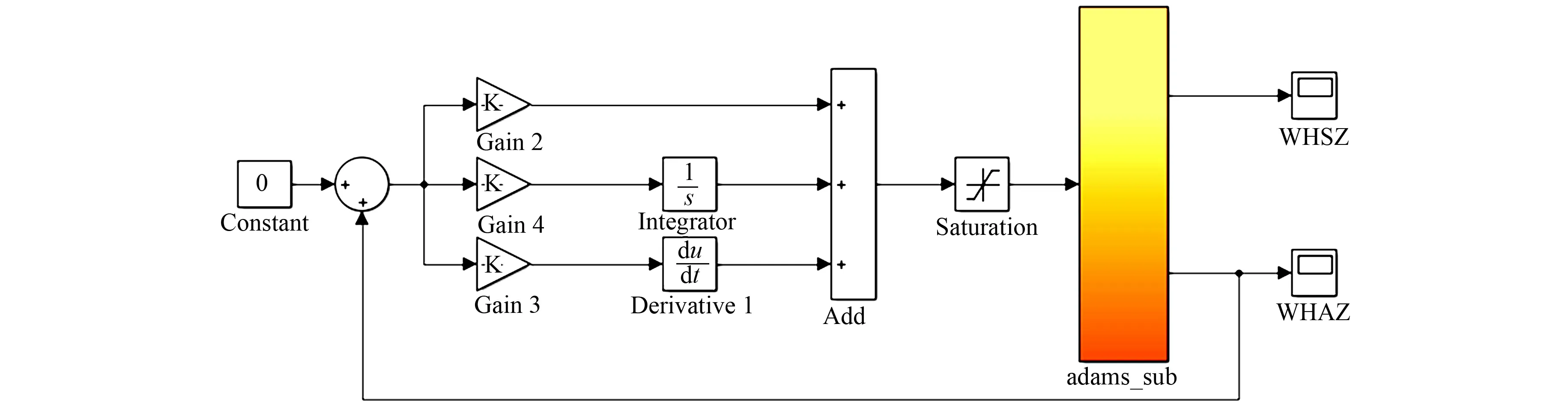
图5 基于PID控制的主动控制联合仿真Fig.5 Active simulation of active control based on PID control
在输出轴齿轮的啮合频率分别为400,500 Hz,即转速为2 028,2 535 r·min-1,负载为1 000 N·mm条件下,进行齿轮传动振动主动控制的仿真对比分析,如图6所示.图6中:a为振动加速度;t为时间;DSP为功率谱密度;f为频率.由图6的时域图可知:两种控制方法都能有效地降低齿轮传动系统的振动,但AFPID控制具有更好的控制效果.由图6的频域图可知:齿轮系统在啮合频率和谐波处的振动能量分布最大,PID控制和AFPID控制都能使各阶主要频率处的幅值明显减小.
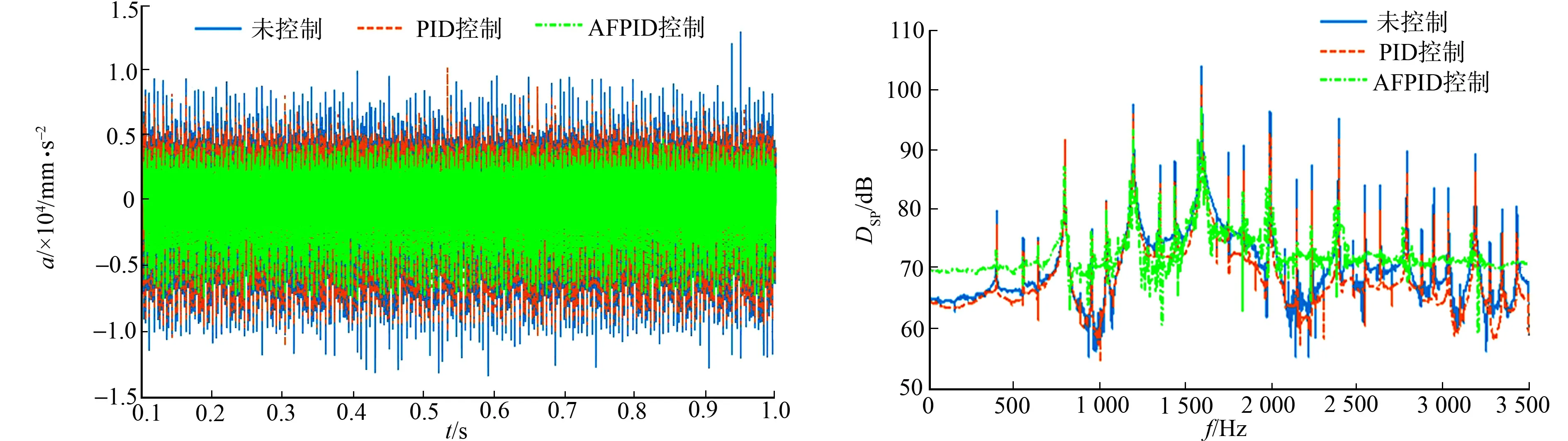
(a) 转速为2 028 r·min-1的时域图 (b) 转速为2 028 r·min-1的频域图
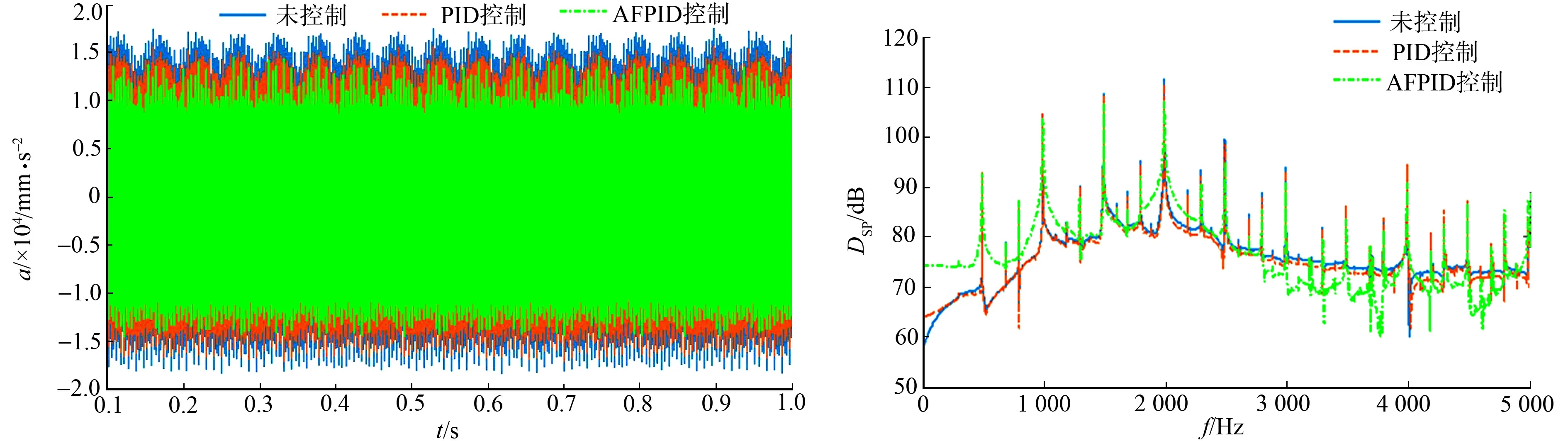
(c) 转速为2 535 r·min-1的时域图 (d) 转速为2 535 r·min-1的频域图图6 不同转速下输出轴时域振动主动控制的仿真分析Fig.6 Simulation analysis of active vibration control of output vibration in output shaft at different speeds
通过对比相同负载、不同转速下的时域图和频域图的控制效果,可以发现当负载等其他条件相同而转速在一定范围内增大时,从时域图可以看出振动幅值有所增大,从频域图上可以看出两种控制算法在各阶频率处的控制效果有所减弱,如表5,6所示.由表5,6可知:对于在齿轮的啮合频率和谐波处的控制效果,AFPID控制优于经典PID控制.当转速为2 028 r·min-1时,齿轮传动系统在三阶谐波处的振动最大,AFPID控制将振动降低了7 dB,降低6.7%;当转速为2 535 r·min-1时,齿轮传动系统同样在三阶谐波处的振动最大,AFPID控制将振动降低了4.4 dB,降低3.9%.
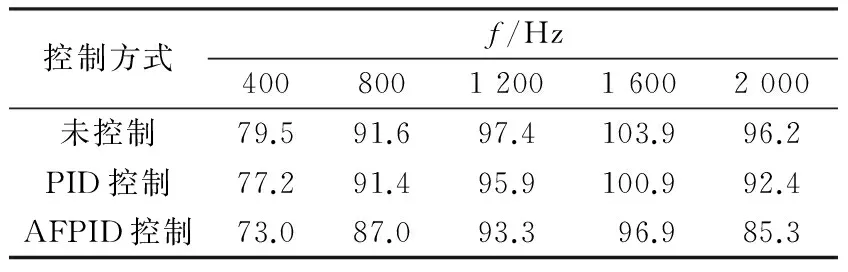
表5 转速为 2 028 r·min-1输出轴 振动在主要频率处的幅值Tab.5 Speed of 2 028 r·min-1 output shaft vibration amplitude at main frequency out

表6 转速为2 535 r·min-1输出轴 振动在主要频率处的幅值Tab.6 Speed of 2 535 r·min-1 output shaft vibration amplitude at main frequency out
6 结论
为了控制齿轮传动系统由于内部激励造成的振动及噪声,采用AFPID控制方法进行主动控制,得到以下3点主要结论.
1) 应用AFPID控制算法在联合仿真中进行主动控制,结果表明,AFPID控制有效地抑制了多个谐波频率上的振动,证明了控制算法正确性及应用在主动控制上的有效性.
2) 将PID控制和AFPID控制进行对比仿真,结果表明,AFPID具有更好的控制效果,在啮合频率和谐波处更有效地抑制了振动,证明了AFPID控制的优越性.
3) 随着电机转速的增大,齿轮传动系统的振动也增大,算法对振动的控制难度也有所提高,即AFPID在低速传动中具有更好的控制效果.
[1] LI Yongzhuo,DING Kang,HE Guolin,etal.Vibration mechanisms of spur gear pair in healthy and fault states[J].Mechanical Systems and Signal Processing,2016,81:183-201.DOI:10.1016/j.ymssp.2016.03.014.
[2] 房怀英,洪尚任,杨建红,等.克林贝格螺旋锥齿轮的建模与仿真[J].华侨大学学报(自然科学版),2004,25(1):67-70.DOI:10.3969/j.issn.1000-5013.2004.01.017.
[3] GUAN Y H,LIM T C,Jr SHEPARD S W.Experimental study on active vibration control of a gearbox system[J].Journal of Sound and Vibration,2005,282(3/4/5):713-733.DOI:10.1016/j.jsv.2004.03.043.
[4] BELANGER P,BERRY A,PASCO Y,etal.Multi-harmonic active structural acoustic control of a helicopter main transmission noise using the principal component analysis[J].Applied Acoustics,2009,70(1):153-164.DOI:10.1016/j.apacoust.2007.12.007.
[5] 李以农,张锋,丁庆中,等.齿轮啮合振动的主动控制方法与实验研究[J].振动工程学报,2014,27(2):215-221.DOI:10.16385/j.cnki.issn.1004-4523.2014.02.004.
[6] 范振华.直齿圆柱齿轮传动弯曲振动主动控制研究[D].重庆:重庆大学,2010:29-37.
[7] 李以农,张锋,王雷,等.次级通道在线辨识的齿轮啮合振动主动控制[J].振动与冲击,2013,32(16):7-12.DOI:10.13465/j.cnki.jvs.2013.16.019.
[8] 李朋志,葛川,苏志德,等.基于动态模糊系统模型的压电陶瓷驱动器控制[J].光学精密工程,2013,21(2):394-399.DOI:10.3788/OPE.20132102.0394.
[9] NIU Jiangchuan,SHEN Yongjun,YANG Shaopu,etal.Analysis of uffing oscillator with time-delayed fractional-order PID controller[J].International Journal of Non-Linear Mechanics,2017,92:66-75.DOI:10.1016/j.ijnonlinmec.2017.03.014.
[10] 郑涛,袁飞,王燕萍,等.基于模糊控制的快速无盲区的频移式孤岛检测法[J].电力系统保护与控制,2014,42(23):38-40.
[11] LIU Xiaoping,WANG Huanqing,GAO Chuang,etal.Adaptive fuzzy funnel control for a class of strict feedback nonlinear systems[J].Neurocomputing,2017,241:71-80.DOI:10.1016/j.neucom.2017.02.030.
[12] ASKARI M R,SHAHROKHI M,TALKHONCHEH M K,etal.Observer-based adaptive fuzzy controller for nonlinear systems with unknown control directions and input saturation[J].Fuzzy Sets and Systems,2017,314:24-45.DOI:10.1016/j.fss.2016.05.004.
[13] DONG Jiuxiang,HOU Junteng.Output feedback fault-tolerant control by a set-theoretic description of T-S fuzzy systems[J].Applied Mathematics and Computation,2017,301:117-134.DOI:10.1016/j.amc.2016.12.017.
[14] 龙凯,程颖.齿轮啮合力仿真计算的参数选取研究[J].计算机仿真,2002,19(6):87-88.DOI:10.3969/j.issn.1006-9348.2002.06.028.
[15] FARSHIDIANFAR A,SAGHAFI A.Identification and control of chaos in nonlinear gear dynamic systems using Melnikov analysis[J].Physics Letters A,2014,378(46):3457-3463.DOI:10.1016/j.physleta.2014.09.060.
[16] KURUSHIN M I,BALYAKIN V B,KURUSHIN S A.Methods of vibration control in elastic systems with gears[J].Procedia Engineering,2015,106:192-201.DOI:10.1016/j.proeng.2015.06.024.
(责任编辑: 陈志贤英文审校: 崔长彩)
Multi-StageGearVibrationActiveControlUsingAdaptiveFuzzyPIDControl
ZHANG Feng, LI Haiyan, WANG Han, SUN Wenhao, LUO Shun′an
(College of Mechanical Engineering and Automation, Huaqiao University, Xiamen 361021, China)
10.11830/ISSN.1000-5013.201704047
2017-04-16
张锋(1979-),男,讲师,博士,主要从事机械振动与噪声控制、汽车系统动力学的研究.E-mail:zhangfeng@hqu.edu.cn.
国家自然科学基金资助项目(51405169); 福建省自然科学基金面上资助项目(2015J01636)
TB 535; N 945.13
A
1000-5013(2017)05-0619-06
