区域崩塌和滑坡规模参数频率分布研究——以秦巴山地宁强县为例*

曹璞源，邱海军，胡 胜，杨冬冬

(1. 西安市地质环境监测站，陕西 西安 710007；2. 西北大学 城市与环境学院，陕西 西安 710127；3. 西北大学 地表系统与灾害研究院，陕西 西安 710127)

区域崩塌和滑坡规模参数频率分布研究
——以秦巴山地宁强县为例*

曹璞源1，邱海军2,3，胡 胜2,3，杨冬冬2,3

(1. 西安市地质环境监测站，陕西 西安 710007；2. 西北大学 城市与环境学院，陕西 西安 710127；3. 西北大学 地表系统与灾害研究院，陕西 西安 710127)

基于假设提出崩塌和滑坡灾害长、宽和厚等规模参数频率分布呈负指数关系，并通过变换负指数关系提出面积和体积等规模参数频率分布简单而有效的计算公式。以秦巴山区宁强县为例，对所提出的公式进行验证。结果表明：①特大型和巨型滑坡、崩塌在控制滑坡、崩塌总面积和总体积中起着重要的作用；②崩塌、滑坡规模参数(长、宽和厚)频率分布符合更简单的指数关系，且用指数关系拟合的规模参数频率曲线不会产生“偏转效应”， 地质灾害参数不仅符合对数正态分布(Normal)，而且符合对数韦伯(Weibull)和Logistic分布；③对于崩塌和滑坡面积与体积规模参数，其实质是长、宽和厚等参数的平方级和立方级，因此，对于其规模参数频率分布求解的一个简单的方法是对面积和体积开平方根和立方根后再用指数分布对其拟合，事实证明其确实呈现一种指数分布；④文中所提出的规模参数频率负指数分布，简捷而有效，便于推广应用。

频率分布；规模参数；区域崩塌；滑坡；陕西宁强

在灾害学研究领域，地质灾害规模参数的频率分布往往具有一定的规律性。尤其是区域崩塌和滑坡的规模参数频率分布曲线对于正确估算任意规模崩塌和滑坡发生的概率非常必要，特别是探索一种简捷而有效的分布方程，对于其推广和应用显得尤为重要[1]。国内外众多地质灾害案例研究表明崩塌、滑坡灾害的面积、体积与其数量呈幂律关系，当这些灾害的体积和面积增大时，它们的数量却急剧减少。也有研究证明当这些灾害规模较小时，崩塌、滑坡在双对数曲线上会出现“偏转效应”，许多研究者也给出了原因解释[2-6]。当然，一些国外研究者力图采用分布曲线来拟合它们的关系，如Malamud等发现截断反伽马(Truncated Inverse Gamma)分布可以很好地描述滑坡面积概率函数[7]；Stark and Hovius认为double Pareto概率分布可以更好的表征新西兰和台湾地区滑坡面积的概率密度函数[8]。而国内这方面的研究较少，只有许强[9]、姚令侃[10]、戴福初[11]等人探索性地研究了规模参数频率的幂指数关系。邱海军等发现用幂函数拟合(即双对数坐标下)的确会出现“偏转效应”，必须用分段函数才能拟合[12]。

综上，对于规模参数频率分布的研究主要集中于面积和体积的频率分布，并且在规模较小时“偏转”严重，拟合效果很不理想。目前还没有学者研究长、宽和厚的规模参数频率分布，而事实上，面积是长和宽参数的平方级，体积是长、宽和厚参数的平方和立方级。显然，这毫无疑问地增加了崩塌、滑坡规模参数频率分布曲线的弯曲程度，客观上也增加了拟合难度系数，“偏转效应”现象由此而生。

众所周知，越是重大的事件其发生的频率和次数反而越低，著名古登堡-里查德(Gutenberg-Richter)关系就符合这一规律[13]，即地震震级越大，发生次数越少，具体来说，震级m与>m的地震频数N满足LogN(>m)=a-bm的数学关系。相似地，崩塌、滑坡的发生是自然和人类活动共同作用的结果[14]，它们的频率分布是否也满足特定的关系呢？这是本文将要解决的科学问题。

本文以崩塌、滑坡的长、宽和厚基本规模参数为基础，分析其规模参数频率的分布特征，并假设长、宽和厚等基本规模参数的频率分布符合最简单的指数分布。而面积、体积参数分别是长、宽和厚等基本规模参数的平方级和立方级，因此，本文又假设面积和体积的平方根和立方根分别符合指数分布。最后通过秦巴山区区域崩塌和滑坡进行验证。

1 研究区概况

宁强县地处秦巴山区，位于陕西省汉中市西南角，地理坐标在105°21′10″～106°35′18″E、32°37′06″～33°12′42″N之间(图1)，国土面积3 246.8 km2，总人口33.96 万人。这里山高谷深、地形起伏大，属于北亚热带湿润性季风气候，降雨充沛。由于受新构造运动影响，宁强县地质环境十分复杂，深大断裂发育，地质灾害(如崩塌、滑坡、泥石流、地面塌陷等)频发，是陕西省地质灾害重灾县。崩塌、滑坡灾害约占地质灾害总数的97%，以滑坡为主。

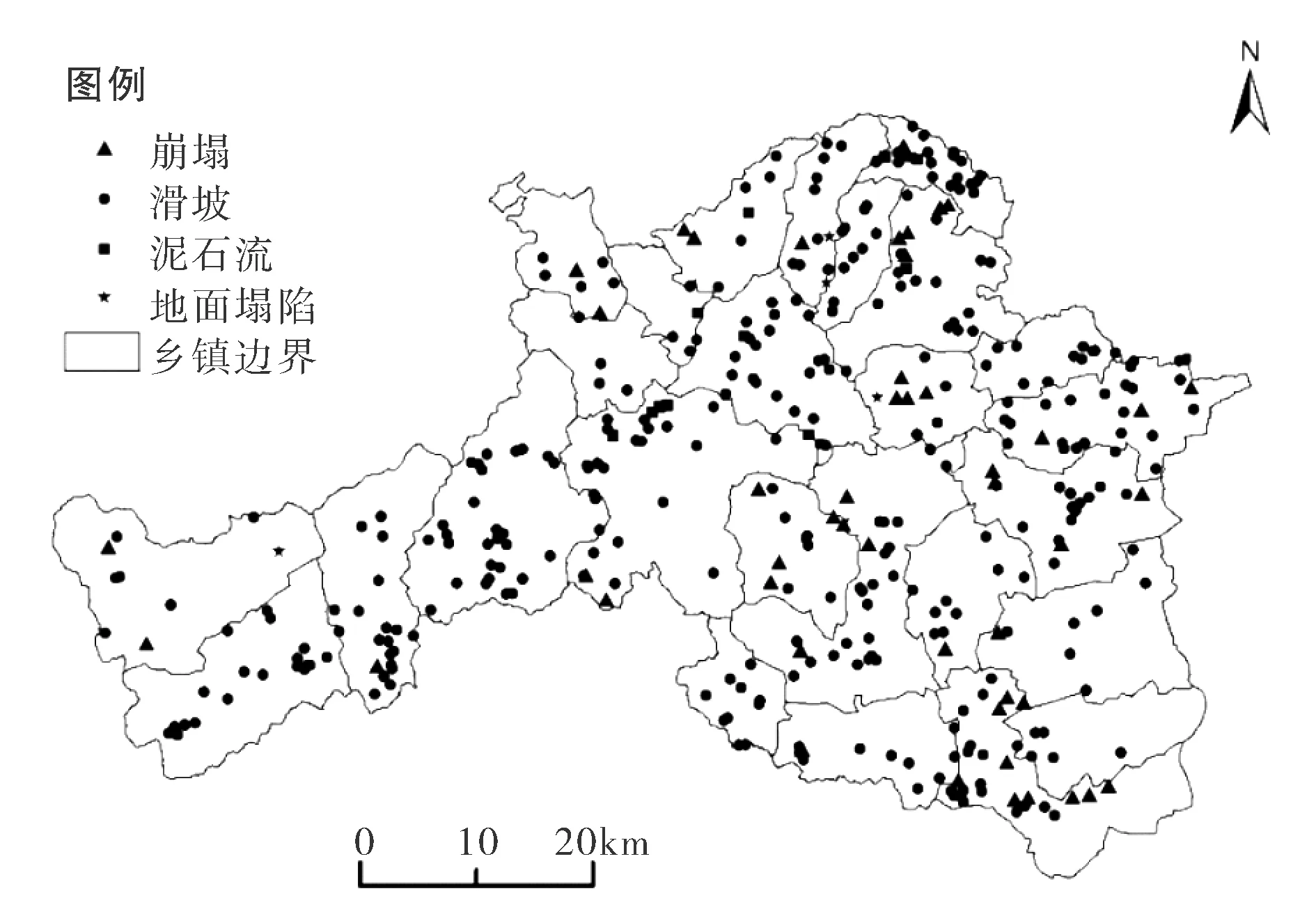
图1 研究区位置与地质灾害分布

2 数据来源与方法

2.1 数据来源

地质灾害数据一部分来源于宁强县国土局，一部分来源于室内遥感解译和野外灾害调查。最终将二者整合，建立了宁强县地质灾害数据库，详细记录了地质灾害的地理位置、数量多少、分布情况、规模大小等数据，研究区共有滑坡329个，崩塌48个(图1)。

2.2 研究方法

崩塌和滑坡的长、宽和厚是描述崩塌和滑坡规模的最基本参数，类比地震学中著名的古登堡-里查德(Gutenberg-Richter)定律，提出崩塌和滑坡长、宽和厚等规模参数的指数分布公式：

lnN=aM+b。

(1)

式中：M为崩塌和滑坡某一规模参数，N为大于或等于该规模参数的崩塌和滑坡个数。

笔者以往的研究已经证实，宁强县滑坡和崩塌规模参数之间存在着幂律相依性。即规模参数体积、面积与长和宽等参数之间符合幂函数关系，在已知其中任何一个参数的情况下都可以通过幂函数求出其它参数[12]。与之类似，面积与体积都能通过一次或二次求幂函数还原到长、宽和厚等参数形式上，从而使其符合上述公式。但是，为了使公式更加简捷，对面积(体积)求平方根(立方根)之后，其规模-频率分布也符合负指数分布。

面积规模参数频率分布：

(2)

体积规模参数频率分布：

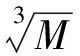
(3)

3 崩塌和滑坡规模参数频率分布分析

3.1 区域崩塌和滑坡规模参数概述

利用宁强县地质灾害编录数据库进行统计后发现(如图2和图3)，特大型和巨型滑坡、崩塌在控制地质灾害的总面积和总体积中扮演着重要角色[15-16]。最大的1个滑坡就可以占到所有滑坡总面积的6.16%，滑坡总体积的26.08%；而最大的15个滑坡就占到总面积的35.6%和总体积的54%(图2)。同样，占总数仅2%的1个最大崩塌却占到崩塌总面积的15%和总体积的30%；而占总数仅10.4%的最大5个崩塌却占到崩塌总面积的55%和总体积的74%(图3)。

3.2 规模参数频率分布实例验证

3.2.1 崩塌和滑坡长、宽和厚频率分布

为了检验崩塌、滑坡的长、宽和厚等规模参数是否真正服从指数分布，我们以秦巴山区宁强县的329处滑坡和48处崩塌为样本，对上述假设进行验证。宁强县地质灾害的长、宽和厚参数在半对数坐标系中表现出负指数的分布规律。从图4、图5和图6不难看出在该坐标系下，崩塌、滑坡的长、宽和厚与累计频率的确表现为指数分布趋势。通过最小二乘法拟合，可以拟合出最佳方程：

滑坡长与频率关系最佳拟合方程为：

lnN=-0.0091M+0.1373，(R2=0.9806，P<0.05)。

(4)

崩塌长与频率关系最佳拟合方程为：

lnN=-0.0332M+0.1235，(R2=0.9792，P<0.05)。

(5)

滑坡宽与频率关系最佳拟合方程为：

lnN=-0.0088M+0.0743，(R2=0.9795，P<0.05)。

(6)

崩塌宽与频率关系最佳拟合方程为：

lnN=-0.0142M-0.1856，(R2=0.9604，P<0.05)。

(7)

滑坡厚与频率关系最佳拟合方程为：

lnN=-0.3679M+0.6604，(R2=0.9461，P<0.05)。

(8)

崩塌厚与频率关系最佳拟合方程为：

lnN=-0.0176M-0.0366，(R2=0.9446，P<0.05)。

(9)

3.2.2 崩塌、滑坡的面积与体积频率分布

对崩塌、滑坡的面积(体积)求平方根(立方根)后，再用指数分布对其拟合可以求解出它们规模参数的频率分布(图7、图8)。

图7、图8表明滑坡、崩塌灾害面积(体积)的平方根(立方根)与累计频率的确也满足负指数分布。

图2 滑坡面积(左)与体积(右)累计图

图3 崩塌面积(左)与体积(右)累计图

图5 滑坡(左)和崩塌(右)的宽与频率的关系图

图6 滑坡(左)和崩塌(右)的厚与频率的关系图

图7 滑坡(左)和崩塌(右)的面积平方根和频率关系图

图8 滑坡(左)和崩塌(右)的体积立方根和频率关系图

滑坡面积与频率关系最佳拟合方程为：

(10)

崩塌面积与频率关系最佳拟合方程为：

(11)

滑坡体积与频率关系最佳拟合方程为：

(12)

崩塌体积与频率关系最佳拟合方程为：

(13)

本文对面积和体积频率分布曲线经过简单的取其平方根和立方根就可以转化为指数分布形式，简捷而有效，便于推广和应用。同时，对于特定的区域a是一个定值，那么a值就可以作为反映这一地区崩塌和滑坡灾害规模和强度的一个值，或者说可以作为这一地区崩塌和滑坡灾害的宏观表征。

3.3 崩塌、滑坡频率与强度的关系

对于频率与强度的关系，相关研究表明虽然截断逆伽马(truncated inverse gamma)分布和double Pareto概率分布在一定情况下能够较好地模拟出崩塌、滑坡面积或者体积规模[12]。然而，这两个分布牵扯太多的参数(有些参数很难获取)，故在某种程度上阻碍了其应用和推广。为了检验宁强县崩塌、滑坡面积与体积对数是否符合正态分布，我们引入统计学中常用的对数正态分布，Q-Q图则是常用的检验模型。Q-Q图(图9)分析表明宁强县崩塌、滑坡面积与体积对数完全符合对数正态性，证明了地质灾害的面积和体积参数具有对数正态分布的特征。通过正态分布检验后，就能轻松实现正态(Normal)、韦伯(Weibull)和Logistic分布的拟合，结果如图10。

图9 崩塌、滑坡面积与体积对数Q-Q图

图10 崩塌、滑坡面积与体积对数分布图

4 结论与讨论

崩塌和滑坡规模-频率分布曲线有助于我们科学认识崩塌、滑坡等地质灾害的分布规律。本文基于最大熵原理首次在理论上推导出崩塌、滑坡灾害的长、宽和厚等规模参数频率负指数分布特征，给出了计算公式，在此基础上，通过对崩塌、滑坡灾害的长、宽和厚等规模参数频率负指数分布公式的修正，给出了面积与体积的规模参数频率分布公式，以秦巴山区宁强县为例，对所提出的公式进行验证，结果表明：

(2)对于特定的区域系数a是一个定值，那么a值就可以作为反映这一地区崩塌和滑坡灾害规模和强度的一个值，或者说可以作为这一地区崩塌和滑坡灾害的宏观表征。崩塌、滑坡面积与体积对数不仅符合对数正态分布(Normal)，而且符合对数韦伯(Weibull)和Logistic分布。

(3)本文推导的规模参数频率分布曲线方程方法虽然简单，但却十分有效，对于揭示崩塌和滑坡频率分布的本质有着重要的意义，也便于推广应用。

为了进一步验证公式的正确性，在未来的研究中，我们将以其他区域崩塌和滑坡为例再次进行验证。同时以沙堆模型进行模拟，测量其长、宽、厚、周长、面积和体积等一系列参数，证明其自组织临界性，并验证其是否符合本文提出的简捷而有效的公式。

[1] Guthrie R H, Evans S G. Magnitude and frequency of landslides triggered by a storm event, Loughborough Inlet, British Columbia[J]. Natural Hazards & Earth System Sciences, 2004, 4(3): 475-483.

[2] Pelletier J D, Malamud B D, Blodgett T, et al. Scale-invariance of soil moisture variability and its implications for the frequency-size distribution of landslides[J]. Engineering Geology, 1997, 48(3/4): 255-268.

[3] Stark C P, Hovius N. The characterization of landslide size distributions[J]. Geophysical Research Letters, 2001, 28(6): 1091-1095.

[4] Guzzetti F, Malamud B D, Turcotte D L, et al. Power-law correlations of landslide areas in central Italy[J]. Earth & Planetary Science Letters, 2002, 195(3/4): 169-183.

[5] Brardinoni F, Church M. Representing the landslide magnitude-frequency relation: Capilano River basin, British Columbia[J]. Earth Surface Processes & Landforms, 2004, 29(1): 115-124.

[6] Eeckhaut M V D, Poesen J, Govers G, et al. Characteristics of the size distribution of recent and historical landslides in a populated hilly region[J]. Earth & Planetary Science Letters, 2007, 256(3/4): 588-603.

[7] Malamud B D, Turcotte D L, Guzzetti F, et al. Landslide inventories and their statistical properties[J]. Earth Surface Processes & Landforms, 2004, 29(6): 687-711.

[8] Stark C P, Hovius N. The characterization of landslide size distributions[J]. Geophysical Research Letters, 2001, 28(6): 1091-1094.

[9] 许强, 黄润秋. 地质灾害发生频率的幂律规则[J]. 成都理工大学学报(自科版), 1997(S1): 93-98.

[10] 姚令侃, 黄艺丹, 杨庆华. 地震触发崩塌滑坡自组织临界性研究[J]. 四川大学学报(工程科学版), 2010, 42(5): 33-43.

[11] Dai F C, Lee C F. Frequency-volume relation and prediction of rainfall-induced landslides[J]. Engineering Geology, 2001, 59(3/4): 253-266.

[12] 邱海军, 曹明明, 刘闻. 地质灾害的幂律相依性：以宁强县为例[J]. 地质科技情报, 2013, 32(3): 183-187.

[13] Bak P, Tang C. Earthquakes as a self-organized critical phenomenon[J]. Journal of Geophysical Research Solid Earth, 1989, 94(B11): 15635-15637.

[14] Eeckhaut M V D, Poesen J, Govers G, et al. Characteristics of the size distribution of recent and historical landslides in a populated hilly region[J]. Earth & Planetary Science Letters, 2007, 256(3/4):588-603.

[15] Hovius N, Stark C P, Allen P A. Sediment flux from a mountain belt derived by landslide mapping[J]. Geology, 1997, 25(3): 231-234.

[16] Guzzetti F, Reichenbach P, Cardinali M, et al. Probabilistic landslide hazard assessment at the basin scale[J]. Geomorphology, 2005, 72(1/4): 272-299.

Abstract:On the assumption that size distribution of landslide and collapse about length, width, and thickness fit negative exponential distribution, this paper put forward the formula about them. Further through modifying the formula of size distribution of length, width and thickness, the paper put forward the formula of size distribution of area and volume. At last, taking Ningqiang County as an example to verify the formula. The result showed that:①Very large and giant landslide and collapse play an important role in controlling their area and volume; ②The frequency distribution of collapse and landslide's scale parameters conforms to a exponential function, and the curve fitted by exponential function does not generate deflection effect. Geological hazard parameters not only conforms to logarithmic Normal distribution (Normal), but conforms to logarithmic Weibull and Logistic distribution. ③For the size parameters of area and volume of landslide, its essence is the parameters such as length, width, and thickness of square and cube, therefore, a simple way to solve the size distribution of the area and volume was fitted after open square root and cube root distribution. It showed that they meet negative exponential distribution, and the fitting effect is good. ④Negative exponential distribution of scale parameter frequency that we proposed is so simple and effective that it is convenient for popularization and application.

Key words:frequency distribution; size distribution; regional collapse; landslide; Ningqiang; Shaanxi

Research on Scale Parameter Frequency Distribution of Regional Collapse and Landslide in Ningqiang County

CAO Puyuan1, QIU Haijun2, 3, HU Sheng2, 3and YANG Dongdong2, 3

(1.MunicipalGeologicEnvironmentMonitoringStationofXi’an,Xi’an710007,China; 2.CollegeofUrbanandEnvironmentalScience,NorthwestUniversity,Xi’an710127,China;3.InstituteofEarthSurfaceSystemandHazards,NorthwestUniversity,Xi’an710127,China)

曹璞源，邱海军，胡胜，等. 区域崩塌和滑坡规模参数频率分布研究——以秦巴山地宁强县为例[J]. 灾害学，2017，32(4)：126-131. [CAO Puyuan, QIU Haijun, HU Sheng,et al. Research on Scale Parameter Frequency Distribution of Regional Collapse and Landslide in Ningqiang County[J]. Journal of Catastrophology，2017，32(4)：126-131.

10.3969/j.issn.1000-811X.2017.04.022.]

X43；P694

A

1000-811X(2017)04-0126-06

2017-02-27

2017-05-05

中国科学院国际合作局对外合作重点项目(131551KYSB20160002)；国家自然科学基金资助项目(41401602)；陕西省自然科学基金(2014JQ2-4021)；西北大学研究生自主创新项目(YZZ15011)

曹璞源(1985-)，男，陕西西安人，助理工程师，从事地质灾害防治与防治研究. Email:76567956@qq.com

邱海军(1983-)，男，陕西神木人，博士，副教授，从事灾害和土地利用研究.Email:rgbitxpl@163.com

10.3969/j.issn.1000-811X.2017.04.022