基于MATLAB的某越野车悬架系统参数计算与仿真分析研究
2017-10-11王红钢徐磊周喻陈晓
王红钢,徐磊,周喻,陈晓
(1.中国汽车工程研究院股份有限公司,重庆 401122;2.重庆长安工业(集团)有限公司,重庆 401120)
基于MATLAB的某越野车悬架系统参数计算与仿真分析研究
王红钢1,徐磊1,周喻2,陈晓1
(1.中国汽车工程研究院股份有限公司,重庆 401122;2.重庆长安工业(集团)有限公司,重庆 401120)
根据车辆参数进行悬架系统受力分析,得到螺旋弹簧所受压缩力;然后结合悬架系统关键参数计算公式和MATLAB/Guide模块,完成GUI界面创建和回调函数程序编写,运行得到刚度、阻尼系数和偏频等参数;最后借助Simulink建立1/2车辆五自由度动力学模型,从车辆垂直振动加速度、悬架动扰度和车轮动载荷3个方面对悬架系统进行仿真分析。引入MATLAB实现了多轴越野车悬架系统参数计算和仿真分析程序化、模块化,对提高设计效率和悬架系统性能分析具有重要意义。
越野车;悬架系统;参数计算;仿真分析
0 引言
多轴越野车具有整车质量大、离地间隙高和行驶路况复杂等特点,因此,设计安全可靠的悬架系统对于多轴越野车具有重要意义。螺旋弹簧为弹性元件、双筒式液压减振器为阻尼元件、不等长叉臂为导向和传力机构的独立悬架是高机动越野车悬架系统的首选。在悬架系统的设计过程中,存在螺旋弹簧和减振器设计计算复杂、悬架系统整车性能匹配分析困难。MATLAB集科学计算、程序编写(Editor)、可视化(Guide)和仿真(Simulink)于一体,对悬架系统参数计算和仿真分析具有快速、准确的特点。作者借助MATLAB工具完成某6×6越野车悬架系统螺旋弹簧、减振器、悬架的参数计算,并对整车行驶性能进行仿真分析。
1 悬架参数计算
某6×6越野车质量为15 776 kg,一桥轴荷为5 008.5×9.8 N,二桥轴荷为5 160×9.8 N,三桥轴荷为5 292.9×9.8 N。将双横臂悬架简化为四连杆机构,如图1所示。
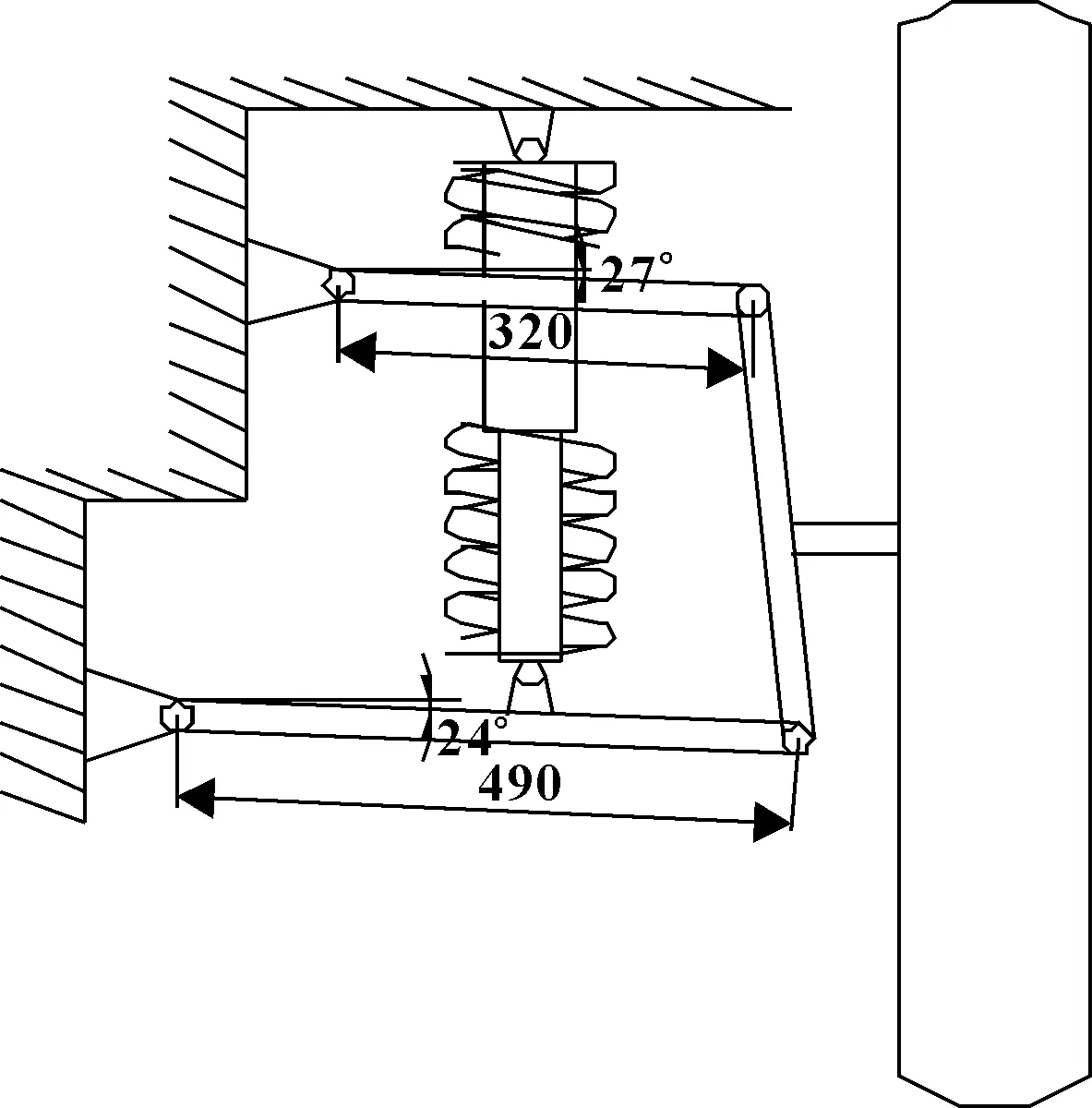
图1 双横臂式独立悬架简图
对图1所示机构简图进行受力分析,可分别得到各桥螺旋弹簧所受压力的大小:一桥为FS1=21 325 N;二桥为FS2=21 876 N;三桥为FS3=22 496 N。结合越野车行驶情况和车辆布置,考虑选取弹簧行程为s=±70 mm,自由高度H0=520 mm。螺旋弹簧材料选择60Si2CrVA弹簧钢,其许用应力为σb=1 863 MPa,弹性模量G=80 000 N/mm2。
MATLAB/GUI可根据设计要求创建GUI应用程序,并且自动生成M文件框架,用户根据M文件框架编制应用程序。根据参数输入输出要求,完成GUI界面布局见图2。
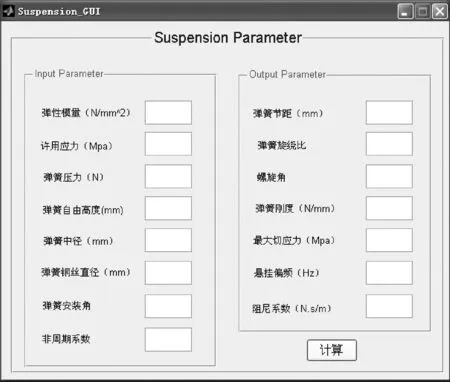
图2 GUI界面布局
运行图2所示的GUI界面,可得一桥弹簧刚度k1=3×105N/m,阻尼系数c1=3.5×104N·s/m;二桥弹簧刚度k2=3.1×105N/m, 阻尼系数c2=3.65×104N·s/m;三桥弹簧刚度k3=3.2×105N/m,阻尼系数c1=3.71×104N·s/m。
2 整车仿真分析
越野车辆悬架要求保证车辆具有良好的行驶平顺性和稳定的轮胎动扰度,因此,基于MATLAB/Simulink建立1/2车辆五自由度模型,从车辆垂直振动加速度、悬架动扰度和车轮动载荷3个方面对悬架系统进行仿真分析。

表1 动力学模型参数表
2.1 路面白噪声模型
路面不平度模型随路面等级和车辆行驶速度变化而变化,且后轮不平度模型相对于前轮不平度模型存在延时效应。依据Laplace变换及传递函数qf、qm和qr,推导路面模型为:
(1)
式中:δ为由空间频率和路面等级决定的常值;v为汽车的行驶速度;w(t)为零均值白噪声随机信号,其强度T=2δvρ2;qf、qm、qr分别为一桥、二桥和三桥的路面激励位移。
鉴于越野车辆路面情况恶劣,拟选择D级路面谱作为激励,将参数带入路面模型,借助Simulink搭建三轴车辆路面仿真模型,如图3所示。
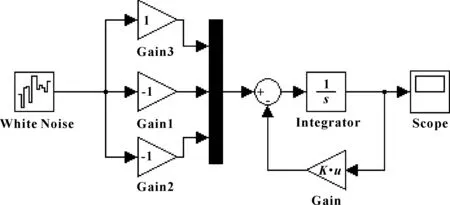
图3 路面激励的Simulink模型
运行图3所示的路面激励模型,可得各轮胎路面激励谱,见图4。

图4 各轮胎路面谱曲线
2.2 车辆仿真分析
文中主要研究越野车车身的垂直振动特性和俯仰特性,因此建立1/2车辆五自由度模型,见图5。

图5 1/2车辆五自由度模型
根据图5所示的越野车模型,可得到下式:
公司将秉承“矿业报国,振兴民族经济”的核心价值观努力发展,将成为世界500强的国际化大型矿业资源跨国公司作为企业目标。

(2)
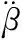
(3)

(4)

(5)

kr(z3-qr)=0
(6)
将动力学方程写成矩阵形式为:

U=[0 0qfqmqr]T;M=diag[mJm1m2m3]
则可以将上式表示为:

(7)
基于1/2车辆五自由度动力学模型和Simulink模块建立1/2车辆仿真模型,见图6。
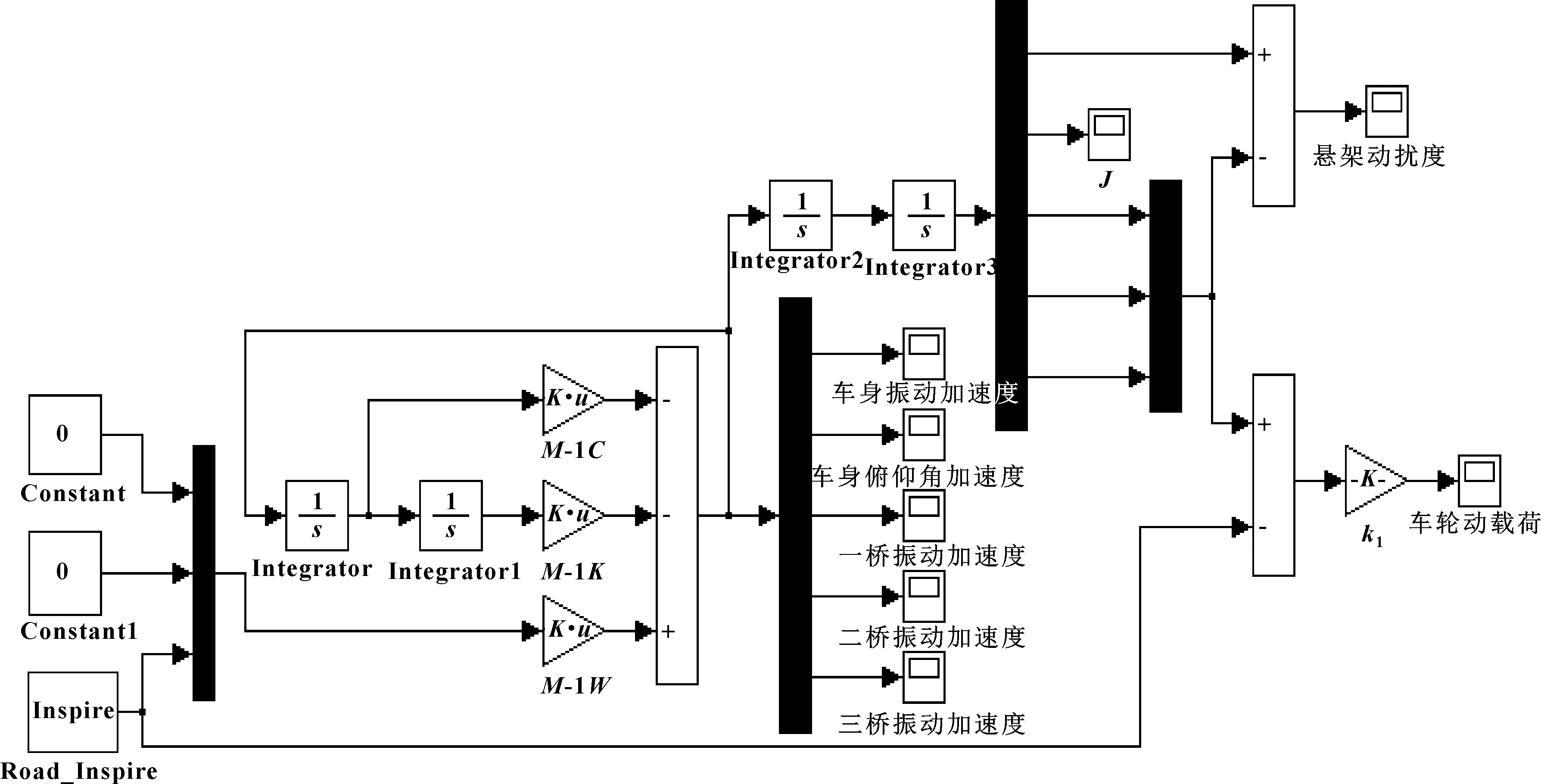
图6 1/2车辆Simulink仿真模型
将表1中的参数带入Simulink中,可分别得到车身垂直振动加速度、悬架动扰度和车轮动载荷,见图7。
由图7所示:车身最大垂直振动加速度amax<6 m/s2,符合越野车辆D级路面车身振动要求;一桥和二桥悬架动行程Zdi

图7 车身加速度、悬架动行程、车轮动载荷时间历程
3 结论
引入MATLAB软件进行悬架参数计算和仿真分析,对于推进悬架系统设计程序化、模块化、集成化具有重要意义。
(1)借助GUI界面实现了悬架参数可视化和程序化计算,能有效提高悬架设计效率。
(2)建立了多轴越野车辆1/2车辆五自由度动力学模型,为研究越野车辆振动特性提供理论基础。
(3)通过搭建Simulink仿真模型,对车辆垂直振动加速度、悬架动扰度和车轮动载荷3个方面进行仿真分析,验证了悬架系统关键参数的合理性。
[1]张英会,刘辉航,王德成,等.弹簧设计手册[M].北京:机械工业出版社,2006.
[2]袁涌,蔡静.Matlab/GUI在钢板弹簧悬架设计中的应用[J].湖北汽车工业学院学报,2011,25(2):16-19. YUAN Y,CAI J.Application of Matlab/GUI in Leaf Spring Suspension Design[J].Journal of Hubei Automotive Industries Institute,2011,25(2):16-19.
[3]彭佳,何杰,李旭宏,等.路面不平度随机激励时域模型的仿真比较与评价[J].解放军理工大学学报(自然科学版),2009,10(1):78-82. PENG J,HE J,LI X H,et al.Simulation Comparison and Evaluation of Common Time Domain Models under Road Irregularity Excitation[J].Journal of PLA University of Science and Technology(Natural Science Edition),2009,10(1):78-82.
[4]于英.多轴越野车辆油气悬架系统参数仿真[J].农业机械学报,2005,36(11):25-28. YU Y.Parametric Simulation of Multiaxile Off-road Vehicle with Hydro-pneumatic Suspension[J].Transactions of the Chinese Society of Agricultural Machinery,2005,36(11):25-28.
[5]吴龙,闻霞.6自由度半车悬架解耦及其分层振动控制的研究[J].汽车工程,2010,32(2):148-154. WU L,WEN X.A Research on the Decoupling of 6 DOF Half Vehicle Suspension and Its Hierarchical Vibration Control[J].Automotive Engineering,2010,32(2):148-154.
ResearchonParametersCalculationandSimulationAnalysisoftheSuspensionSystemofaCertainWheeledArmoredVehicleBasedonMATLAB
WANG Honggang1,XU Lei1,ZHOU Yu2,CHEN Xiao1
(1.China Automotive Engineering Research Institute Co., Ltd., Chongqing 401122, China;2.Chongqing Chang’an Industry(Group) Co., Ltd., Chongqing 401120,China)
The compressive strength of the spiral spring was gotten through force analysis of the suspension system based on the parameters of the vehicle.The interface of the Guide was established and the callback function procedure was compiled combining with computational formula of the key parameter of the suspension system and MATLAB/Guide module,and the parameters of the stiffness, damping coefficient and deviation frequency were gotten.Then,the 5-DOF dynamical model of the 1/2 vehicle was established through Simulink,the simulation analysis was carried out on the suspension system from three aspects including the vertical vibration acceleration, suspension dynamic vehicle immunity and wheel dynamic load. The introduction of MATLAB achieved programmed and modularization for the parameter calculation and simulated analysis of the suspension system of multi-axle wheeled armored vehicle;meanwhile, it’s of great significance on improving the design efficiency and performance analysis of the suspension system.
Wheeled armored vehicle; Suspension system;Parameter calculation;Simulated analysis.
TTJ81
A
1674-1986(2017)09-033-04
10.19466/j.cnki.1674-1986.2017.09.007
2017-08-21
王红钢(1984—),男,研究生,工程师,研究方向为整车测试评价。E-mail:xuleijy@126.com。
