多元函数微分的变量代换
2017-10-10林美琳
林美琳
(莆田学院 数学学院,福建 莆田 351100)
数理研究
多元函数微分的变量代换
林美琳
(莆田学院 数学学院,福建 莆田 351100)
学生在学习多元函数微分的变量代换时,相对比较困难.针对教材,从三个方面归纳总结了这类型题目的解题方法,这样使学生能够全面地掌握这一部分的内容,并能做到举一反三.
多元函数;变量代换;自变量;因变量
目前,本学院用的《数学分析》的教材是复旦大学数学系主编的,此教材在介绍多元函数微分的变量代换时,只有一个例题,而课后关于这方面的练习题倒比较多.很多同学在学这一内容时比较困难,他们觉得很抽象,做题目无从入手.而这一部分内容特别是对考研的同学尤为重要.纵观各高校的考研题,此类型题目出现的机会也是很经常的.而且工科学生在研究生入学考试中,遇到此类题目也感到束手无策.因此,本文从三个方面归纳了多元函数微分的变量代换题型的解题方法.这样可以使学生比较系统的学习这一部分内容,做起题目可以得心应手,并能做到举一反三.
1 在含有导数的式子中的变量代换
在式子 F=Φ(x,y,y',y",…)中,需要把 x,y转换成新的变量:t(自变量)和u(因变量),由x=f(t,u),g=g(t,u)进行微分得到:

类似地可以表示出高阶导数y",….


例 2 设 x=rcosθ,y=rsinθ,变换方程

2 在含有偏导数的式子中自变量的代换

以此类推,可以算出高阶偏导数.
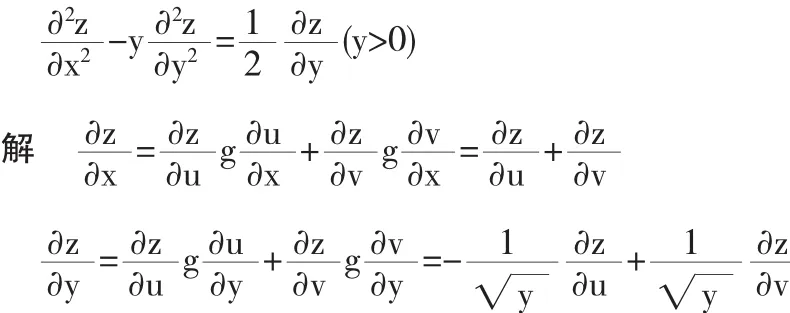


3 在含有偏导数的式子中自变量和因变量的代换
这种情况下,一般是由方程w=w(x,y,z)解出z=f(x,y,w),然后两边同时对x,y求偏导得





〔1〕滕兴虎,郑琴,周华任,廖洪林.吉米多维奇数学分析习题集精选详解(下册)[M].南京:东南大学出版社,2011.
〔2〕钱吉林.数学分析题解精粹[M].武汉:崇文书局,2003.
〔3〕欧阳光中,朱学炎,金福临,陈传璋.数学分析(第三版)[M].北京:高等教育出版社,2007.
O175.25
A
1673-260X(2017)09-0001-02
2017-05-16
