碳纤维增强重组竹梁的极限挠度计算方法

周爱萍，王超,刘睿，沈玉蓉，周梦婕，袁吉，张苏鹏，陶洁

(1.南京林业大学土木工程学院； 2.江苏省林业资源高效利用协同创新中心，南京 210037; 3.南京工业大学建筑学院，南京 211800)

碳纤维增强重组竹梁的极限挠度计算方法

周爱萍1,2，王超1,刘睿1，沈玉蓉1,2，周梦婕3，袁吉1，张苏鹏1，陶洁1

(1.南京林业大学土木工程学院； 2.江苏省林业资源高效利用协同创新中心，南京 210037; 3.南京工业大学建筑学院，南京 211800)

重组竹力学性能优于木材，非常适用于装配式梁柱结构。重组竹抗压强度高于普通混凝土材料，受压应力-应变关系非线性特征明显，但其弹性模量仅为混凝土弹性模量的1/2左右。采用碳纤维(CFRP)增强重组竹梁可充分利用重组竹的抗压性能，提高梁的承载能力，但其非线性变形更加显著。考虑重组竹的受压非线性本构关系，提出计算梁极限挠度的弹性理论修正计算方法。该方法将梁简化为带塑性铰的杆件，假设非线性变形仅发生在塑性铰区域，杆件其余部分始终处于弹性工作状态，将梁的变形分为弹性变形与塑性变形。通过截面应变分析，得到塑性变形的计算公式，进而得到CFRP增强重组竹梁的非线性变形计算公式。CFRP增强重组竹梁的四点弯曲试验表明，所提出的计算方法具有足够的精度。

碳纤维；重组竹；非线性变形；力学模型

竹子作为建筑结构材料受到了越来越多的关注，但原竹不规则的外形与变异性很大的力学性能限制了其在建筑结构材料领域的广泛应用[1-3]。重组竹(parallel strand bamboo，PSB)是一种竹基复合材料，由原竹丝束顺纹组坯热压而成。重组竹的几何形状规则，物理力学性能一致、稳定，可满足现代建筑结构的需求。由于在制造过程中剔除了原竹的缺陷，因此，重组竹具有良好的力学性能，许多指标优于木材，是一种优良的建筑结构材料[4-6]。

重组竹的抗压强度约为60 MPa，远超C30混凝土的抗压强度；而弹性模量约为11 GPa，刚度远低于混凝土和钢材，仅为C30混凝土的1/2、钢材的1/20左右[7-8]。因此，在极限状态时，重组竹梁的挠度远大于相同边界与荷载条件的混凝土梁或钢梁。此外，由于重组竹材料受压本构关系的非线性特性，重组竹梁的荷载-挠度曲线呈显著的非线性特征。碳纤维(CFRP)增强重组竹梁可充分利用重组竹的抗压性能，提高梁的承载力，但其变形的非线性特征更加明显。考虑重组竹材料的受压非线性，建立CFRP增强重组竹梁的极限挠度，是重组竹梁极限状态设计的关键问题，也是重组竹梁非线性分析面临的挑战。全球几乎所有的现行木结构设计规范均采用线弹性理论计算木构件的挠度，这种计算方法对于正常使用状态的变形验算是适用的，但在极限状态下，梁的荷载-挠度曲线早已超出承载力与变形比例极限，故极限变形的计算应采用非线性分析方法。近20年，人们对CFRP增强木构件的承载能力和破坏模式等开展了大量研究[9-14]，但鲜见其极限挠度计算方法的相关报道。

笔者基于线弹性理论，考虑重组竹材料的受压非线性本构关系，提出了一种CFRP增强重组竹梁极限变形的弹性理论修正计算方法，并通过简支梁四点受弯试验，验证计算模型的合理性。

1 材料本构关系

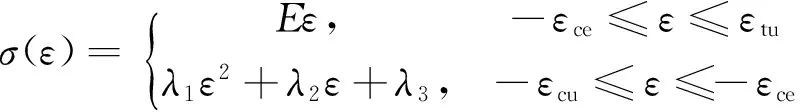
(1)

式中:E为重组竹的弹性模量;λ1、λ2和λ3为材料常数；下标t表示受拉、c表示受压、e和u分别表示弹性极限和最终极限状态。根据连续性和相容性条件,σ(εce)=σce,σ(εcu)=σcu,d(εcu)/dε=0,可以得出:

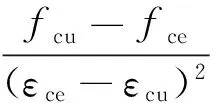
(2)

式中:ftu(公式(1)中当ε=εtu时，f=Eεtu=ftu)和εtu、fce和εce、fcu和εcu分别为重组竹的拉压强度和相应的应变。参照ASTM D143-2014中单轴受拉、受压试验的相关要求,将试验分为A、B两组,每组12个试件测定重组竹材料参数,结果见表1。

表1 PSB顺纹力学参数Table 1 Mechanical properties of PSB in parallel-to-grain direction

CFRP的抗拉本构关系可表示为:

σ(ε)=Erε, 0≤ε≤εrtu

(3)

式中:Er为CFRP的弹性模量;frtu(当ε=εrtu时,σ(ε)=frtu)和εrtu分别为抗拉强度与相应的应变。CFRP的力学参数可参照ASTM D3039/D3039M-2014进行测定,结果见表2。重组竹与CFRP的应力-应变关系曲线如图1所示。

表2 CFRP力学参数Table 2 Mechanical properties of CFRP

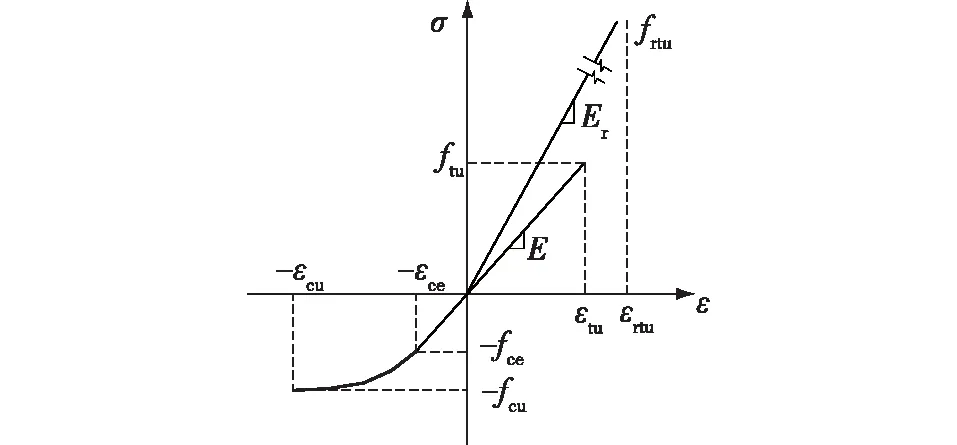
图1 PSB顺纹及CFRP抗拉本构关系Fig.1 Parallel-to-grain constitutive relation of PSB and CFRP

2 极限变形计算模型

当荷载超过比例极限后,梁受压区的重组竹进入受压屈服工作状态,材料的应力-应变关系不再保持线性关系。相应地,CFRP梁的荷载-挠度曲线偏离原直线状态。梁在非线性工作阶段会产生受压区纤维局部屈曲、裂纹萌生与扩展、CFRP脱黏等复杂损伤机理。事实上,梁发生破坏时,仅在破坏截面附近一定范围内发生非线性损伤,而在此范围之外的大部分区域,梁仍处于弹性工作阶段。因此,计算梁挠度时,可将梁简化为带塑性铰的杆件,杆件始终处于弹性工作状态,而非线性变形仅发生在塑性铰上。在塑性铰区域,进一步假定:①塑性铰具有一定长度,其变形符合平截面假定;②CFRP与PSB黏结牢固,无滑移现象;③当试件破坏时,CFRP的应变与PSB梁受拉区最外层极限抗拉应变保持一致。

PSB梁变形分析模型见图2。根据图2b所示破坏截面的极限状态,设最终的极限状态可以分两步达到:①假设受弯截面的中性轴保持在弹性弯曲状态位置不变,增加荷载至极限承载力Fu。根据平截面假设,此时截面的应变分布如图2b中的虚线所示。由于在假想受力状态时材料处于完全弹性工作状态,因此,梁的挠度可采用弹性理论计算。② 保持荷载值Fu不变,放松塑性铰,让其转动至真正的极限状态。此时,破坏截面的中性轴下移,受拉区应变值εtu保持不变,受压区应变值增加至极限应变,截面的应变分布如图2b中的实线所示。因此,梁的极限挠度δu可分为假想弹性挠度δe和假想塑性挠度δp两个部分,即:

δu=δe+δp

(4)

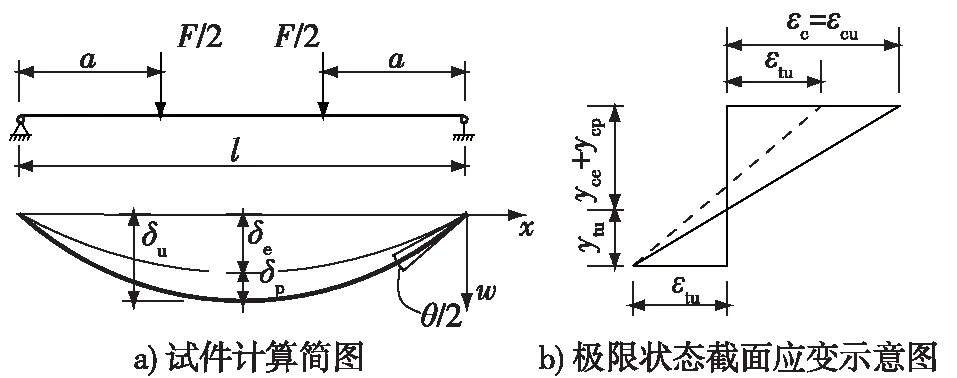
图2 PSB梁变形分析模型Fig.2 Calculation model of PSB beam for deflection analysis

对于图2a所示的四点弯曲梁,基于欧拉理论,弹性变形可以表达如下:

(5)

式中：w为梁的挠度；E′为CFRP增强PSB的等效模量；I′为截面等效惯性矩;E′I′为试件等效抗弯刚度；l为梁的跨度。E′I′=M/Φ,其中,M和Φ分别为梁的弯矩和曲率,公式(5)结合边界条件和连续性条件积分可得:

(6)

分别以Φ=Fx/(2E′I′)和Φ=Fa/(2E′I′)代入公式(6)中的w1和w2，可得:

(7)

因此,跨中弹性变形可以采用下式表示:

(8)

对于假想塑性挠度的计算,设塑性铰段对应于假想弹性状态和极限状态的曲率分别为Φe和Φu,根据截面所在位置梁的曲率与截面应变分布之间的关系可得:

Φe=εtu/(h/2),Φu=εtu/ytu

(9)

式中,ytu和h分别为截面受拉区高度和截面高度。若保持外荷载不变,则使截面发生假想塑性转动引起的曲率变化为:

ΔΦ=Φu-Φe=εtu(1/ytu-2/h)

(10)

考虑塑性铰内一长为ds的微段,则其由假想塑性转动引起的转角为:

dθ=ΔΦds

(11)

梁的假想塑性转动为:

(12)

式中,Lp为塑性铰长度。由几何关系的杆件可知杆端转角为θ/2(图2a),则梁跨中假想塑性挠度为:

(13)

由公式(13)可以看出,假想塑性挠度取决于塑性铰的长度。但由于破坏机理的复杂性,塑性区域实际上是不规则的,也不存在所谓的塑性铰长度。计算表明,若假设塑性铰长度等于梁的截面高度,即得到较好的结果:

(14)

3 试验验证

3.1 试验方案

为验证上述计算方法,进行了A、B两组共6根重组竹梁的四点弯曲试验。每组有1根对比梁,其余2根为CFRP增强梁。两组梁分别采用不同的截面尺寸,试件参数见表3。CFRP的粘贴参照GB 50367—2013《混凝土结构加固设计规范》和CECS 146:2003《碳纤维片材加固混凝土结构技术规程》(2007版)的相关要求进行,需严格控制CFRP与重组竹之间的粘贴工艺,确保试件加载期间不发生滑移现象。

表3 试件参数Table 3 The parameters of specimens

注：U、R分别代表无、有CFRP。

参照ASTM D198-15的相关要求进行梁的四点弯曲试验,试验装置见图3。采用300 kN电液伺服加载试验机进行单调加载,以2.5 mm/min加载速度位移控制加载,确保试件在20 min左右破坏,以忽略材料蠕变的影响。在试件跨中下方布置YHD-50型激光位移计,测定梁跨中位移。在梁跨中沿着截面高度平均分布5个电阻应变片(尺寸为3 mm×20 mm,灵敏系数为2.06),测定试件加载截面变形情况,以验证平截面假定。荷载、位移和截面应变均由TDS-530数据采集仪同步采集,采集频率为1 Hz。

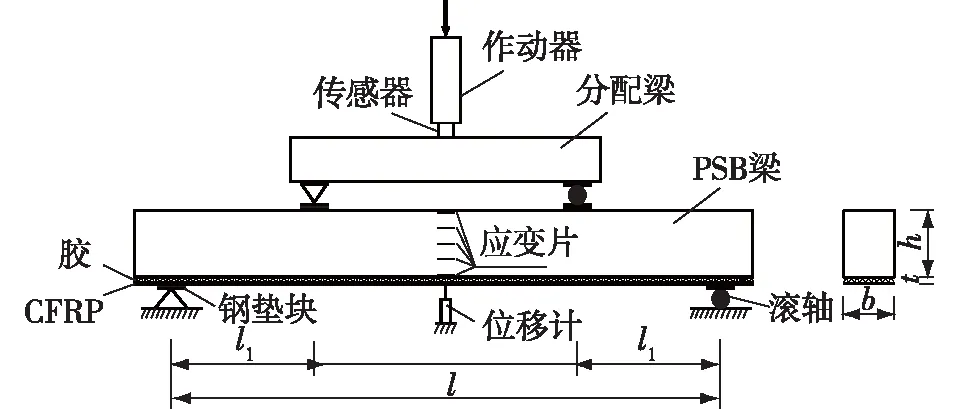
图3 四点弯曲试验装置示意图Fig.3 Test setup of four-point bending experiments

3.2 试验结果与分析

典型的破坏形态与跨中荷载-位移曲线分别见图4和5。由图4可以将CFRP增强重组竹梁的破坏机理简单概括如下:当梁受压区最外层的应力达到材料的抗压比例值时,梁开始进入非线性工作状态;随着加载的持续,受压区的非线性区域不断向内扩展,梁受拉区开始不断出现裂纹,导致梁的刚度持续衰减。在此过程中,截面中和轴开始不断偏离梁截面几何中心,向梁受拉区移动,裂纹不断扩展、延伸;最后,梁受拉区最外层应力达到材料抗拉强度极限值,跨中底部纤维断裂,CFRP与重组竹剥离、断裂。从典型的试件破坏形态中可以看出,断裂的竹纤维导致CFRP撕裂破坏,并非CFRP达到极限抗拉强度而拉断。因此,CFRP的强度未得到充分利用,对重组竹梁的增强作用有限。

图4 破坏形态Fig.4 The failure mode

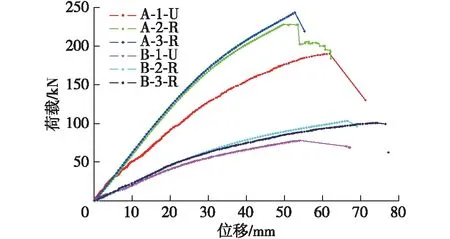
图5 跨中荷载-位移曲线Fig.5 Mid-span load-deflection curves of specimens

从图5中可以看到,荷载-位移曲线经历了线性阶段和非线性强化阶段,梁最后的极限状态处于非线性状态。第一阶段,当荷载低于抗压比例极限值时,构件处于弹性工作阶段,比例极限荷载值约为极限荷载的1/3～1/2;第二阶段,随着不断地加载,梁顶部受压区应力超过抗压比例值,最外层受压区开始进入塑性阶段,处于非线性状态;随着加载的持续,塑性区不断向梁受压区内部扩展,而梁的受拉区始终处于弹性工作阶段。当荷载增加至一定值时,梁底部开始不断出现细微裂缝,刚度开始衰减;最后,随着裂缝不断扩展延伸,梁底部跨中竹纤维断裂,CFRP与PSB剥离,并随之断裂,试件也随之破坏。

跨中挠度试验值与计算值的对比见表4。从表中可以看到,二者吻合良好,表明笔者提出的计算方法有足够的精确度。同时,CFRP增强对梁刚度的提高作用不是很显著,原因可以从上述破坏机理分析中得到,即CFRP并非由应力达到受拉强度极限值而断裂,而是被重组竹梁底部受拉区断裂的竹纤维撕裂。因此,CFRP的增强作用受到了限制。

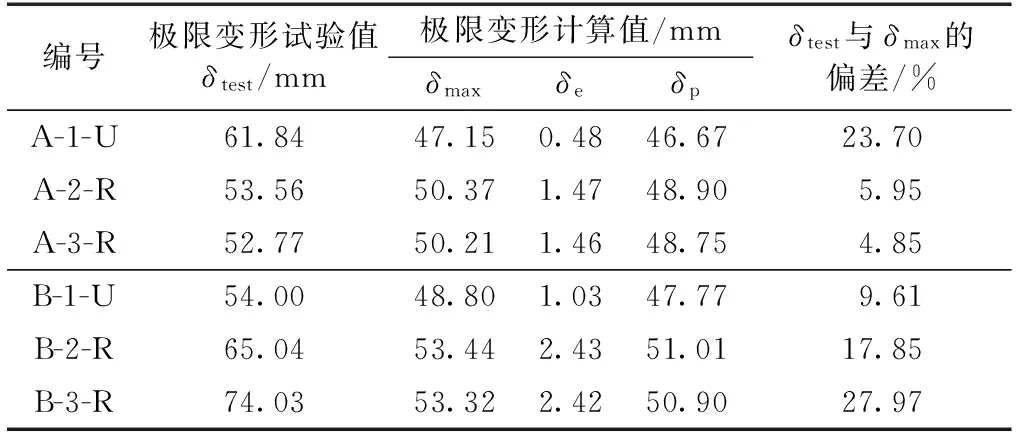
表4 跨中挠度试验值与计算值的对比Table 4 Comparison between tested value and calculated value of mid-span deflection

注：A、B组剪跨比分别为457和500，梁计算长度为1 700 mm，计算值δmax=δe+δp。

4 结 论

重组竹材料受压力学性能的非线性决定了重组竹梁极限状态呈显著的非线性变形特征,尤其是CFRP增强重组竹梁,极限状态下的挠度计算必须考虑重组竹材料的受压非线性本构关系。笔者将重组竹梁简化为带塑性铰的弹性杆件,假设非线性变形仅发生在塑性铰区域,杆件其余部分始终处于弹性工作状态,将梁的变形分为弹性变形与塑性变形,提出了考虑重组竹材料受压力学非线性性能的CFRP增强重组竹梁的极限变形弹性理论修正计算方法,并通过简支梁四点弯曲试验,验证了该计算模型的准确性。试验结果表明,采用CFRP增强重组竹梁对梁的刚度提高不显著。由于受拉区断裂的竹纤维撕裂了CFRP,其强度不能充分发挥。

[1]JANSSEN J J A.Mechanical properties of bamboo[M].Eindhoven:Springer,Netherlands,1991.

[2]KHALIL H P S A,BHAT I U H,JAWAID M,et al.Bamboo fiber reinforced biocomposites:a review[J].Materials and Design,2012,42:353-368.

[3]ZHOU A P,HUANG D S,LI H T,et al.Hybrid approach to determine the mechanical parameters of fibers and matrixes of bamboo[J].Construction and Building Materials,2012,35:191-196.

[4]HUANG D S,BIAN Y L,ZHOU A P,et al.Experimental study on stress-strain relationships and failure mechanism of parallel strand bamboo made from phyllostachys[J].Construction and Building Materials,2015,77:130-138.

[5]周爱萍,刘睿,沈玉蓉,等.碳纤维增强重组竹受弯构件的极限承载力试验[J].林业工程学报,2017,2(3)：137-142.ZHOU A P,LIU R,SHEN Y R,et al.Experiment study on ultimate load-bearing capacity of carbon fiber reinforced polymer reinforced parallel bamboo beam[J].Journal of Forestry Engineering,2017,2(3)：137-142.

[6]章卫钢,江文正,唐荣强.重组竹短期抗弯蠕变特性及其微观结构研究[J].林业工程学报,2017,2(3)：33-37.ZHANG W G,JIANG W Z,TANG R Q.Study on short-term bending creep behavior microstructure banmboo scrimber[J].Journal of Forestry Engineering,2017,2(3)：33-37.

[7]HUANG D S,ZHOU A P,BIAN Y L.Experimental and analytical study on the nonlinear bending of parallel strand bamboo beams[J].Construction and Building Materials,2013,44:585-592.

[8]HUANG D S,BIAN Y L,HUANG D M,et al.An ultimate-state-based-model for inelastic analysis of intermediate slenderness PSB columns under eccentrically compressive load[J].Construction and Building Baterials,2015,94:306-314.

[9]BELPERIO R,GRAD I E.The performance of gluam beams reinforced with carbon fibre[C]∥Proceedings of Pacific Timber Engineering Conference,New Zealand,1999:99-106.

[10]BORRI A,CORRADI M,GRAZINI A.A method for flexural reinforcement of old wood beams with CFRP materials[J].Composites Part B:Engineering,2005,36(2):143-153.

[11]LI Y F,XIE Y M,TSAI M J.Enhancement of the flexural performance of retrofitted wood beams using CFRP composite sheets[J].Construction and Building Materials,2009,23(1):411-422.

[12]RAFTERY G M,HARTE A M.Low-grade glued laminated timber reinforced with FRP plate[J].Composites Part B:Engineering,2011,42(4):724-735.

[13]FANG H,SUN H M,LIU W Q,et al.Mechanical performance of innovative GFRP-bamboo-wood sandwich beams:experimental and modelling investigation[J].Composites Part B:Engineering,2015,79:182-196.

[14]GENTRY R.Performance of glued-laminated timbers with FRP shear and flexural reinforcement[J].Journal of Composites for Construction,2011,15(5):861-870.

[15]TIMOSHENKO S.History of strength of materials[M].New York:McGraw Hill,1953.

Ultimate deformation calculation method of carbon fiber reinforced polymer reinforced parallel strand bamboo beams

ZHOU Aiping1,2,WANG Chao1,LIU Rui1,SHEN Yurong1,2,ZHOU Mengjie3,YUAN Ji1,ZHANG Supeng1,TAO Jie1

(1.School of Civil Engineering,Nanjing Forestry University;2.Jiangsu Co-innovative Center for Efficient Application of Forestry Resources,Nanjing 210037,China； 3.School of Architecture,Nanjing TECH University,Nanjing 211800,China)

With good mechanical properties,parallel strand bamboo (PSB) is superior to wood and increasingly used to be beams and columns in building constructions.The compressive strength of PSB is higher than the commonly used concrete materials,and the compressive stress-strain relationship exhibits pronounced nonlinear deformation,while the elastic modulus of PSB is lower than half of the C30 concrete modulus.Carbon fiber reinforced polymer (CFRP) reinforced PSB beams could fully develop the compressive nonlinearity of PSB,and increase the load-carrying capacity and show more significant ductility than those of the unreinforced one.Thus,PSB beams exhibit pronounced nonlinear deformation under the ultimate state.In this study,we proposed a modified calculating method based on the elastic theory of the ultimate deformation of the beam by considering the nonlinear constitutive relationship of PSB.The method simplified the beam to be a bar with a plastic hinge,presumed that the nonlinear deformation only occurred in the plastic hinge region,and the rest of the bar was always in elastic state.The deformation of the beam was divided into the elastic deformation and plastic deformation.The calculation formula of the plastic deformation was developed through the analysis of the cross-section strain,and the formula of the nonlinear deformation of CFRP reinforced PSB beams was put forward.The calculated method proposed in this study was validated through four-point bending experiments of CFRP reinforced PSB beams.The results showed that the model results well agreed with the test ones.

carbon fiber reinforced polymer (CFRP);parallel strand bamboo (PSB);nonlinear deformation;mechanical model

TU531.3

A

2096-1359(2017)05-0115-05

2016-11-21

2017-05-05

“十三五”国家质量基础的共性技术研究与应用专项(2017YFF0207200)；国家自然科学基金(51578291)；林业科学技术成果国家级推广项目([2015]21)；江苏高校优势学科建设工程资助项目(PAPD)；江苏省大学生创新创业训练计划项目(201510298049Z)。

周爱萍，女，副教授，研究方向为现代竹/木结构。E-mail:zaping2007@163.com