基于经验模态分解互信息熵与同步压缩变换的微地震信号去噪方法研究

秦 晅,蔡建超,刘少勇,卞爱飞

(中国地质大学(武汉)地球物理与空间信息学院,地球内部多尺度成像湖北省重点实验室,湖北武汉430074)

基于经验模态分解互信息熵与同步压缩变换的微地震信号去噪方法研究

秦 晅,蔡建超,刘少勇,卞爱飞

(中国地质大学(武汉)地球物理与空间信息学院,地球内部多尺度成像湖北省重点实验室,湖北武汉430074)

针对微地震信号具有随机性、非平稳性与时频耦合的特点以及经验模态分解(Empirical Mode Decomposition,EMD)的模态混叠问题,提出了基于经验模态分解互信息熵与同步压缩变换(Synchrosqueezing Transform,SST)的微地震信号去噪方法。首先对微地震信号进行经验模态分解,获得从高频到低频排列的固有模态函数(Intrinsic Mode Function,IMF)分量;然后求取相邻固有模态函数分量之间的互信息熵,从而辨识出高频与低频部分的分界;最后利用同步压缩变换提取高频部分的有效信号,将其与低频部分重构,实现微地震信号的有效去噪。利用不同噪声强度的理论模型和实际资料,对本文方法与直接舍弃高频成分的去噪方法进行了对比,结果表明,本文方法能够很好地去除微地震信号中的混叠噪声,并将有效信号从噪声中提取出来,提高了资料的信噪比。

微地震信号;经验模态分解;同步压缩变换;互信息熵;重构;噪声压制

微地震监测技术作为获得地层裂缝分布的一种较为有效方法,已经在油气田开发与煤矿开采等领域得到了广泛应用[1]。由于微地震波能量微弱,检波器采集到的微地震信号存在大量随机噪声,因而后续的初至拾取、震源定位及裂缝解释工作会受到很大影响[2-3],因此,需要对微地震信号进行滤波、去噪等处理,将微地震有效信号从噪声中分离出来。

传统的傅里叶变换是信号去噪的有效方法,但对于具有非平稳信号特点的微地震信号去噪效果不佳[4-5]。连续小波变换在低频部分具有较高的频率分辨率,在高频部分具有较高的时间分辨率,能够在时频域很好地区分非平稳信号的突变部分,但去噪结果受到Heisenberg不确定性和小波基函数选取的影响[6-9]。经验模态分解(EMD)是一种信号自适应分解方法,已经在生物医学的信号处理、机械设备的检测与故障诊断、地震勘探的信号处理[10-14]等领域得到了广泛的应用,但其稳定性会受到模态混叠现象的影响[15-16]。

针对EMD中出现的模态混叠现象,WU等[15]在信号中加入功率谱密度均匀分布的白噪声,使其在不同尺度上具有连续性的特征,给出了总体平均经验模态分解方法;YEH等[16]通过加入正、负成对的辅助噪声,提出了互补集合经验模态分解方法。上述方法能在一定程度上抑制模态混叠现象,但计算的复杂程度会显著上升。

本文根据微地震信号具有随机性、非平稳性与时频耦合的特点,兼顾EMD出现的模态混叠问题,提出了基于EMD互信息熵与同步压缩变换(SST)的微地震信号去噪方法。模型测试和实际资料处理验证了方法的有效性与实用性。

1 方法原理

在实际微地震信号去噪中,有效信号往往位于低频部分,所以通常把高频成分的固有模态函数(IMF)分量作为噪声直接去除,重构原信号剩余的IMF分量即可实现压制噪声的目的[11,17-18]。但是,简单地舍弃高频成分会丢失部分有效信息,造成去噪效果不佳,因此需要发展一种有效剔除混叠噪声并保留有效信号的方法。

1.1 IMF互信息熵成分辨识

EMD算法将时间序列信号自适应地分解成一组含有不同尺度的IMF分量,能够较好地处理非平稳信号,它不依赖于基函数的选取。EMD得到的IMF必须满足以下两个条件[11-16]:①IMF中极值点的个数与过零点的个数相等或最多相差一个;②在任意数值点处,由局部极大值与极小值确定的包络线均值为0。

经过EMD后,微地震信号s(t)可以表示为：

(1)

式中:SIMFi(t)表示频率从高到低排列的IMF分量;rn(t)表示残差分量,代表信号的平均趋势。将公式(1) 改写为：

(2)

互信息熵用于衡量两个随机变量之间的统计依存性[18-21],其表达式为：

(3)

式中:p(xi,yj)为联合概率分布;p(xi)和p(yj)为边缘概率分布;X和Y表示不同的IMF分量;r和s分别是X和Y的符号数量。

假设高频成分为噪声干扰,低频成分为有效信号,利用IMF分量之间的互信息熵关系可以辨识出高频与低频成分的分界。由EMD得到的IMF分量特征可知：高频噪声对每一个IMF分量的依存性逐渐降低,而低频有效信号对每一个IMF分量的依存性逐渐增强。因此,可以假设高频成分与低频成分是部分相互统计独立的。由互信息熵的特点可知：两个相互独立的随机变量之间的互信息熵应等于0[18,22]。所以,在计算每个相邻IMF分量之间的互信息熵时会出现局部极小值,只需搜索第一个局部极小值即得到高频成分与低频成分的分界。于是可得以下搜索目标函数：

(4)

式中:k为高频成分与低频成分分界处的IMF分量序号。

1.2 基于同步压缩变换的混叠噪声压制改进算法

SST算法是在小波变换的基础上发展起来的一种时频域重排算法,但与原始重排算法不同的是,其在提高时频分辨率的同时,也能够支持信号的重构[23-27]。由于SST能够获得较高频率精度的时频谱,使得各频率曲线之间不存在交叉项,因此可以较好地解决频率的混叠问题。利用SST实现高频成分混叠噪声压制的步骤如下：

1) 对高频成分H(t)进行连续小波变换,得到小波变换系数W(ωl,b),并计算其瞬时频率ω(a,b)。

(5)

式中:n表示信号采样点数。

3) 利用计算得到的瞬时频率建立(b,a)→(b,ω(a,b))之间的映射关系,对时间-尺度平面的能量进行重新分配,将其转化为时间-频率平面,使得中心频率ωl相邻区间[ωl-Δω/2,ωl+Δω/2]的值被压缩到ωl上[28],获得SST系数T(ωl,b),其离散形式为

(6)

4) 利用SST获得的高分辨率时频谱确定有效信号的时间与频率范围,再对其进行SST重构,获得信号x(t),实现对高频成分混叠噪声的压制。

(7)

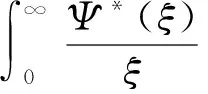
将高频成分混叠噪声压制后的信号x(t)与剩余的低频成分有效信号进行重构,即可实现对微地震信号噪声的去除。

2 测试与应用

2.1 模型测试

为了验证本文去噪方法的可行性,采用如图1所示的井中微地震观测系统,利用有限差分正演方法模拟了一个井中16级检波器接收的微地震记录(图2),数据采样间隔为0.5ms,采样点数为1000。将图2模拟的微地震记录加入高斯白噪声,加噪后数据的信噪比为0.3,如图3 所示,从中抽取一道数据进行去噪处理。图4为抽取的单道记录加噪前、后波形及其频谱,对单道加噪信号进行自适应EMD,得到8个IMF分量以及对应的频谱,如图5所示。可以看出每一个IMF分量都有不同的振幅,而且分解的频率按照从高到低的顺序排列。

利用互信息熵公式(3)计算相邻IMF分量之间的互信息量,结果如表1所示。按照本文1.1节所给的高频部分与低频部分分界点判定方法,可知IMF34为出现的第一个极小值,所以IMF4即为加噪信号的高频部分与低频部分分界点,图5中IMF4的波形以及对应的频谱也验证了判定结果的正确性。图6为将IMF4之后的分量叠加获得的低频部分信号和SST的结果,从中可以看出低频部分的噪声含量较低,可以将低频部分当作有效信号进行处理。

图1 井中微地震观测系统

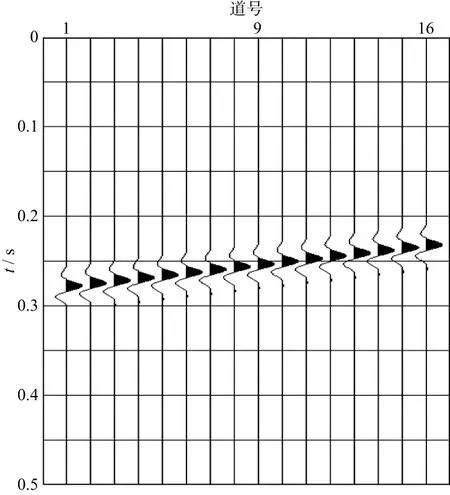
图2 微地震记录

图3 加噪后微地震记录

图4 原信号、含噪信号及其频谱a 原信号; b 原信号频谱; c 含噪信号; d 含噪信号频谱

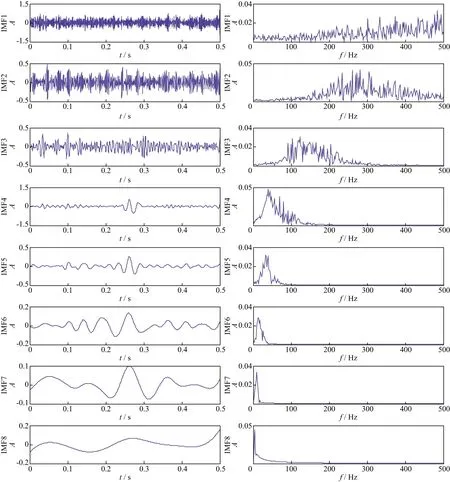
图5 含噪信号EMD及其频谱

IMF分量IMF12IMF23IMF34IMF45IMF56IMF67IMF78系数0.93290.98640.57790.68481.43800.86171.0580

利用1.2节给出的SST混叠噪声压制方法,对IMF4之前的分量叠加组成的高频部分进行同步压缩变换,去除混叠噪声,如图7所示。图7a为IMF4之前的分量叠加组成的高频部分信号,从中可以看出噪声基本上分布在高频部分。图7b和图7c分别为高频部分短时傅里叶变换(SIFT)和SST时频谱,可以看出,SIFT时频谱模糊,不能很好地分辨出有效信号,而SST时频谱具有较高的频率精度,各时频曲线间不存在交叉项,提高了有效信号脊线的分辨率,也证明了SST能够较好地改善频率混叠现象。图7d为SST自适应阈值去噪后的时频谱,可以看出高频部分的噪声得到了很好的压制。图7e为对高频部分有效信号进行提取后得到的有效信号,将其与剩余的低频部分进行重构,即可得到降噪后的信号。

图8对比了单道加噪信号直接舍弃高频分量的去噪结果和本文方法的去噪结果,图9对比了图3所示的微地震加噪记录直接舍弃高频分量的去噪结果和本文方法的去噪结果。可以看出,直接舍弃高频分量去噪的方法虽然能够压制噪声,但同时使有效信号频率出现部分缺失,并且还混叠了部分噪声,造成了有效信号的波形畸变与衰减;而本文方法不仅很好地压制了噪声,而且使有效信号的波形得到了较好保持。定义去噪后信号与原信号的差值为含有的噪声,信号与噪声能量的比值为信噪比RSN[27,29]：

图6 低频部分信号(a)和同步压缩变换结果(b)

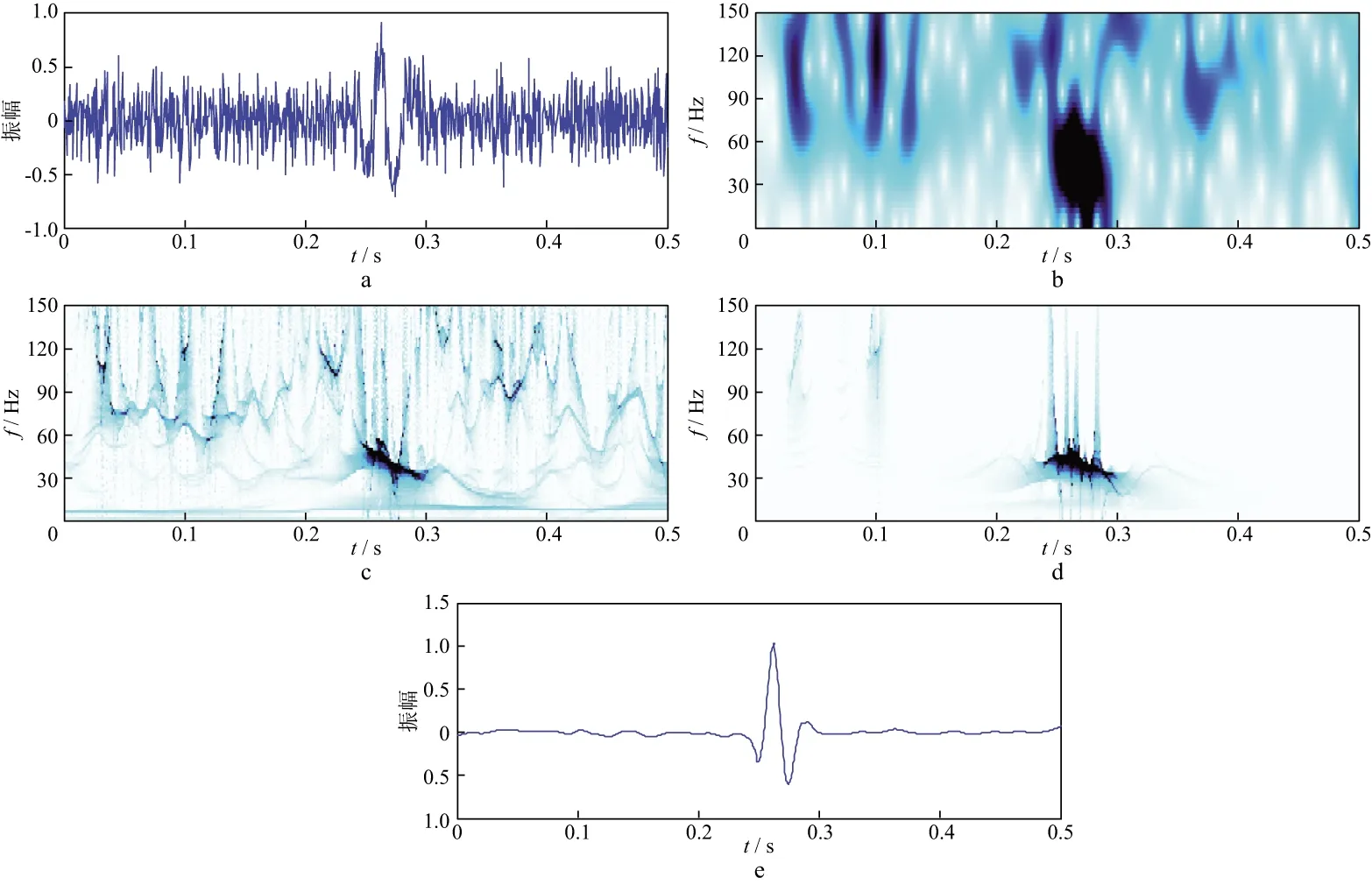
图7 同步压缩变换混叠噪声压制效果a 高频部分信号; b SIFT时频谱; c SST时频谱; d SST自适应阈值去噪后时频谱; e SST提取的有效信号

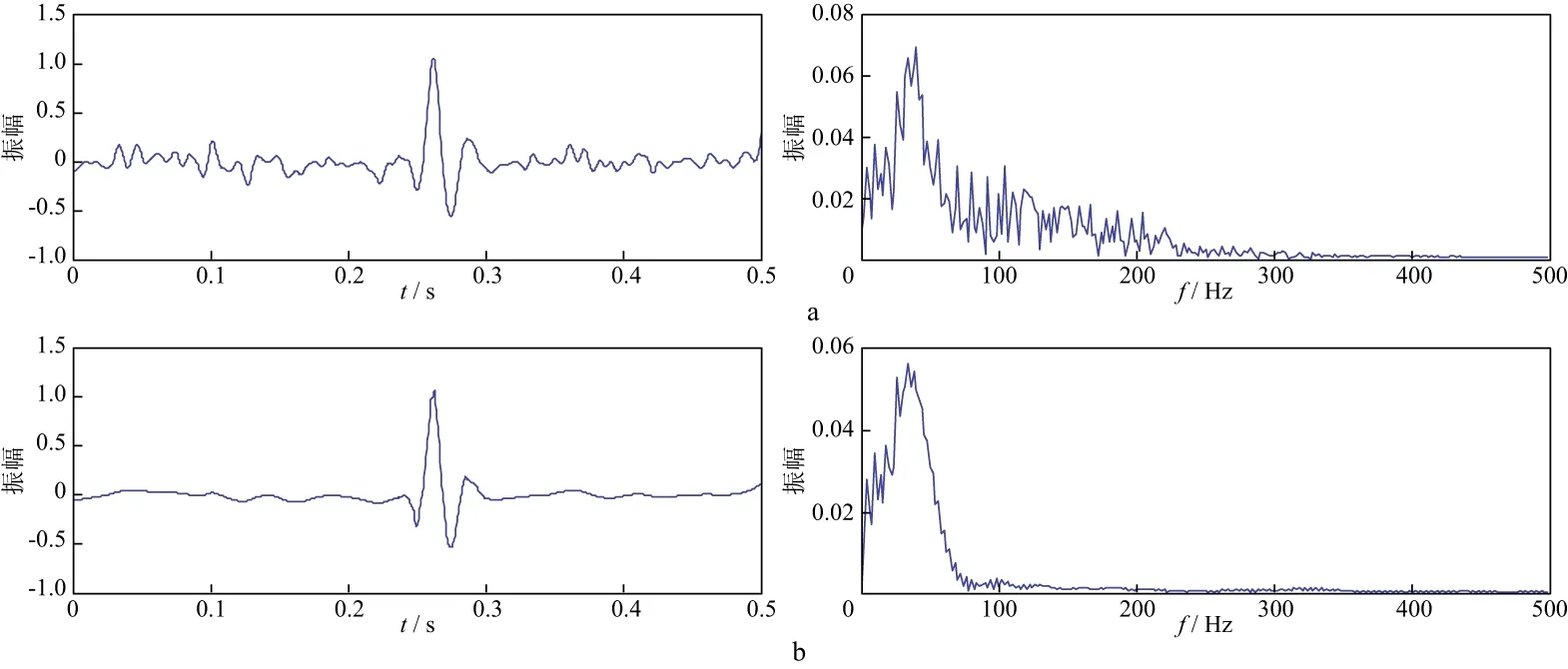
图8 单道加噪信号应用不同方法去噪的效果对比a 直接舍弃高频分量; b 本文方法

图9 加噪记录应用不同方法去噪的效果对比a 直接舍弃高频分量; b 本文方法

(8)

式中:M表示原信号;S为去噪后信号。由公式(8)计算直接舍弃高频分量方法去噪后的信噪比为2.43,本文方法去噪后的信噪比为6.67,定量说明了本文方法去噪的有效性。

不断地改变含噪信号的信噪比,观察不同噪声水平下两种方法的去噪效果,并计算去噪后的信噪比,结果如表2所示。可以看出,在不同噪声水平下,两种方法都能提高含噪信号的信噪比,但是本文方法具有更好的去噪效果。

2.2 应用实例

本文截取某油田压裂的一段井中微地震有效事件数据进行了去噪效果分析,如图10所示。原始数据由16级三分量检波器接收,采样间隔为0.25ms,采样点数为1000。图10a中1～16,17～32,33～48道分别为数据的z,x,y分量,由于数据的信噪比较低,噪声几乎淹没了有用的微地震信号,无法清晰地识别出P波、S波。图10b为对原始数据进行EMD后直接去除高频成分的结果,可以看出,虽然高频噪声被滤除,但是微地震有效信号同相轴仍然不够清晰,有效信号波形发生了畸变。图10c为利用SST方法[27]提取的结果,可以看出,SST方法虽然较好地提取了有效信号,但是混叠了部分噪声,说明噪声压制还不够彻底。图10d为利用本文方法去噪后的结果,原始数据的噪声得到了很好压制,有效信号的波形也得到了很好保持,为后续的初至拾取、震源定位及裂缝解释工作奠定了基础。

表2 不同噪声水平下不同方法去噪后的信噪比

图10 实际微地震数据去噪效果对比a 原始数据; b 直接舍弃高频成分去噪结果; c SST提取结果; d 本文方法去噪结果

3 结束语

本文针对微地震信号具有随机性、非平稳性与时频耦合的特点,以及EMD存在的模态混叠问题,利用同步压缩变换能提高信号时频分辨率,同时支持信号重构的优点,提出了基于EMD互信息熵与同步压缩变换的微地震信号去噪方法。不同噪声强度的理论模型测试和实际资料分析表明,该方法能够很好地去除信号中的混叠噪声,较好地将有效信号从噪声中提取出来,提高资料信噪比,为后续的初至拾取、震源定位及裂缝解释等工作奠定了基础。

[1] MAXWELL S.Microseismic:growth born from success[J].The Leading Edge,2010,29(3):338-343

[2] 宋维琪,何可,郭全仕,等.微地震资料自适应滤波方法研究[J].石油物探,2013,52(3):229-233 SONG W Q,HE K,GUO Q S,et al.Micro-seismic data adaptive filtering method[J].Geophysical Prospecting for Petroleum,2013,52(3):229-233

[3] 杨心超,朱海波,崔树果,等.P波初动震源机制解在水力压裂微地震监测中的应用[J].石油物探,2015,54(1):43-50 YANG X C,ZHU H B,CUI S G,et al.Application of P-wave first-motion focal mechanism solutions in microseismic monitoring for hydraulic fracturing[J].Geophysical Prospecting for Petroleum,2015,54(1):43-50

[4] ALVANITOPOULOS P F,PAPAVASILEIOU M,ANDREADIS I,et al.Seismic intensity feature construction based on the Hilbert-Huang transform[J].IEEE Transactions on Instrumentation and Measurement,2012,61(2):326-337

[5] GACI S.The use of wavelet-based denoising techniques to enhance the first-arrival picking on seismic traces[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(8):4558-4563

[6] SINHA S,ROUTH P S,ANNO P D,et al.Spectral decomposition of seismic data with continuous-wavelet transform[J].Geophysics,2005,70(6):19-25

[7] BEENAMOL M,PRABAVATHY S,MOHANALIN J.Wavelet based seismic signal de-noising using Shannon and Tsallis entropy[J].Computers & Mathematics with Applications,2012,64(11):3580-3593

[8] 盛冠群,李振春,王维波,等.基于小波分解与高阶统计量的微地震初至拾取方法研究[J].石油物探,2015,54(4):388-395 SHENG G Q,LI Z C,WANG W B,et al.A new automatic detection method of microseismic events based on wavelet decomposition and high-order statistics[J].Geophysical Prospecting for Petroleum,2015,54(4):388-395

[9] 王小杰,栾锡武.基于小波分频技术的地层Q值提取方法研究[J].石油物探,2015,54(3):260-266 WANG X J,LUAN X W.Q value extraction method based on wavelet frequency division technology[J].Geophysical Prospecting for Petroleum,2015,54(3):260-266

[10] BATTISTA B M,KNAPP C,MCGEE T,et al.Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data[J].Geophysics,2007,72(2):H29-H37

[11] 李月,彭蛟龙,马海涛,等.过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法[J].地球物理学报,2013,56(2):626-634 LI Y,PENG J L,MA H T,et al.Study of the influence of transition IMF on EMD de-noising and the improved algorithm[J].Chinese Journal of Geophysics,2013,56(2):626-634

[12] 董烈乾,李振春,杨少春,等.基于经验模态分解的f-x域面波压制方法[J].石油地球物理勘探,2013,48(1):42-48 DONG L Q,LI Z C,YANG S C,et al.Ground roll suppression inf-xdomain based on empirical mode decomposition[J].Oil Geophysical Prospecting,2013,48(1):42-48

[13] HAN J,MIRKO V D B.Microseismic and seismic denoising via ensemble empirical mode decomposition and adaptive thresholding[J].Geophysics,2015,80(6):KS69-KS80

[14] 薛雅娟,曹俊兴.聚合经验模态分解和小波变换相结合的地震信号衰减分析[J].石油地球物理勘探,2016,51(6):1148-1155 XUE Y J,CAO J X.Seismic attenuation analysis using ensemble empirical mode decomposition and wavelet transform[J].Oil Geophysical Prospecting,2016,51(6):1148-1155

[15] WU Z,HUANG N E.A study of the characteristics of white noise using the empirical mode decomposition method[J].Proceedings Mathematical Physical & Engineering Sciences,2004,460(2046):1597-1611

[16] YEH J R,SHIEH J S,HUANG N E.Complementary ensemble empirical mode decomposition:a novel noise enhanced data analysis method[J].Advances in Adaptive Data Analysis,2010,2(2):135-156

[17] 贾瑞生,赵同彬,孙红梅,等.基于经验模态分解及独立成分分析的微震信号降噪方法[J].地球物理学报,2015,58(3):1013-1023 JIA R S,ZHAO T B,SUN H M,et al.Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis[J].Chinese Journal of Geophysics,2015,58(3):1013-1023

[18] 梁喆,彭苏萍,郑晶.基于EMD和互信息熵的微震信号自适应去噪[J].计算机工程与应用,2014,50(4):7-11 LIANG Z,PENG S P,ZHENG J.Self-adaptive denoising for micro seismic signal based on EMD and mutual information entropy[J].Computer Engineering and Applications,2014,50(4):7-11

[19] SHANNON C E.A mathematical theory of communication[J].The Bell System Technical Journal,1948,27(4):379-423

[20] 李辉,戴旭初,葛洪魁,等.基于互信息量的地震信号检测和初至提取方法[J].地球物理学报,2007,50(4):1190-1197 LI H,DAI X C,GE H K,et al.Seismic signal detection and first arrival pickup based on mutual information[J].Chinese Journal of Geophysics,2007,50(4):1190-1197

[21] 秦晅,宋维琪.基于时窗能量比与互信息量的微地震初至拾取方法[J].物探与化探,2016,40(2):374-379 QIN X,SONG W Q.Automatic first arrival pickup method of microseismic event based on energy ratio and mutual information[J].Geophysical and Geochemical Exploration,2016,40(2):374-379

[22] OMITAOMU O A,PROTOPOPESCU V A,GANGULY A R.Empirical mode decomposition technique with conditional mutual information for denoising operational sensor data[J].IEEE Sensors Journal,2011,11(10):2565-2575

[23] 尚帅,韩立国,胡玮,等.压缩小波变换地震谱分解方法应用研究[J].石油物探,2015,54(1):51-55 SHANG S,HAN L G,HU W,et al.Applied research of synchrosqueezing wavelet transform in seismic spectral decomposition method[J].Geophysical Prospecting for Petroleum,2015,54(1):51-55

[24] HERRERA R H,HAN J,VAN DER BAANM.Applications of the synchrosqueezing transform in seismic time-frequency analysis[J].Geophysics,2014,79(3):V55-V64

[26] HERRERA R H,TARY J B,VAN DER BAAN M,et al.Body wave separation in the time-frequency domain[J].IEEE Geoscience and Remote Sensing Letters,2015,12(2):364-368

[27] 秦晅,宋维琪.基于同步压缩变换微地震弱信号提取方法研究[J].石油物探,2016,55(1):60-66 QIN X,SONG W Q.Weak signal extraction method of microseismic data based on synchrosqueezing transform[J].Geophysical Prospecting for Petroleum,2016,55(1):60-66

[28] 汪祥莉,王斌,王文波,等.混沌干扰中基于同步挤压小波变换的谐波信号提取方法[J].物理学报,2015,64(10):11-20 WANG X L,WANG B,WANG W B,et al.Harmonic signal extraction from chaotic interference based on synchrosqueezed wavelet transform[J].Acta Physica Sinica,2015,64(10):11-20

[29] 王姣,李振春,王德营.基于CEEMD的地震数据小波阈值去噪方法研究[J].石油物探,2014,53(2):164-172 WANG J,LI Z C,WANG D Y.A method for wavelet threshold denoising of seismic data based on CEEMD[J].Geophysical Prospecting for Petroleum,2014,53(2):164-172

(编辑：戴春秋)

MicroseismicdatadenoisingmethodbasedonEMDmutualinformationentropyandsynchrosqueezingtransform

QIN Xuan,CAI Jianchao,LIU Shaoyong,BIAN Aifei

(HubeiSubsurfaceMulti-scaleImagingKeyLaboratory,InstituteofGeophysicsandGeomatics,ChinaUniversityofGeosciences,Wuhan430074,China)

On the basis of the characteristics of randomness,non-stationarity,time-frequency coupling of microseismic data,and of the problem of modal aliasing in empirical mode decomposition (EMD),this paper proposes a microseismic data denoising method based on EMD mutual information entropy and synchrosqueezing transform (SST).First,the microseismic signal is decomposed by EMD to acquire the intrinsic mode function (IMF) sequencing from high to low frequency.Next,the mutual information entropy of adjacent IMF components is calculated to identify the boundary between the high-frequency and the low-frequency part.Finally,the effective signal of the high-frequency part is extracted by the SST and reconstructed with the low-frequency part to achieve an effective microseismic data denoising.We applied the method to synthetic data sets with different noise intensities and to field data,and the results showed that this method can better remove the aliasing noise,extract the effective signal,and improve the SNR,compared with denoising methods that directly discard the high-frequency components.

microseismic,empirical mode decomposition,synchrosqueezing transform,mutual information entropy,reconstruction,denoising

P631

：A

1000-1441(2017)05-0658-09DOI:10.3969/j.issn.1000-1441.2017.05.006

秦晅,蔡建超,刘少勇,等.基于经验模态分解互信息熵与同步压缩变换的微地震信号去噪方法研究[J].石油物探,2017,56(5):666

QIN Xuan,CAI Jianchao,LIU Shaoyong,et al.Microseismic data denoising method based on EMD mutual information entropy and synchrosqueezing transform

[J].Geophysical Prospecting for Petroleum,2017,56(5):666

2017-01-09;改回日期：2017-03-14。

秦晅(1988—),男,博士在读,主要研究方向为微观岩石物理与信号处理。

蔡建超(1981—),男,教授,博士生导师,主要从事微观岩石物理研究。

国家重点研发计划(2016YFC060110304)、国家自然科学基金(41572116)、中央高校基本科研业务费专项资金(CUG160602)联合资助。

This research is financially supported by the State Key Program of National Natural Science of China (Grant No.2016YFC060110304),the National Nature Science Foundation of China (Grant No.41572116) and the Fundamental Research Funds for the Central Universities (Grant No.CUG160602).