基于低秩矩阵恢复的去噪方法在石油测井中的应用

王艳伟,夏克文,牛文佳,Ali Ahamd

(1.河北工业大学电子信息工程学院,天津300401;2.河北省大数据计算重点实验室,天津300401)

基于低秩矩阵恢复的去噪方法在石油测井中的应用

王艳伟1,2,夏克文1,2,牛文佳1,2,Ali Ahamd1,2

(1.河北工业大学电子信息工程学院,天津300401;2.河北省大数据计算重点实验室,天津300401)

随着测井技术的发展,各大油田采集和存储的测井数据量呈井喷式增长,并存在大量冗余和噪声,在进行油气层识别前必须对测井数据进行压缩和去噪等预处理。低秩矩阵恢复(Low-Rank Matrix Recovery,LRMR)理论将压缩感知(Compressed Sensing,CS)中向量样例的稀疏表示推广到矩阵的低秩情形,从较大但稀疏的误差中恢复出本质上低秩的数据矩阵,可更好地保持数据结构,提高去噪效果。因此将低秩矩阵恢复理论中的去噪方法应用于石油测井中,实现对测井数据的去噪处理。对比研究了加速近端梯度算法(Accelerate Proximal Gradient,APG)、精确增广拉格朗日乘子(Exact Augmented Lagrange Multipliers,EALM)法和非精确增广拉格朗日乘子法(Inexact Augmented Lagrange Multipliers,IALM)在测井数据中的去噪效果,对去噪前后的测井数据分别采用支持向量机(Support Vector Machine,SVM)和相关向量机(Relevance Vector Machine,RVM)进行油气层识别,结果表明,与不去噪情况相比,利用三种算法进行去噪处理后油气层识别精度都有了显著提升。通过参数优化减少迭代次数,可使得IALM算法在运算时间上优于EALM算法和APG算法,明显提高了运算效率。

石油测井;数据去噪;低秩矩阵恢复;加速近端梯度算法;增广拉格朗日乘子法

在油气测井过程中,所得测井数据量庞大,其中必定存在大量的数据冗余和噪声[1],在进行油气层识别前需要进行数据压缩和去噪等预处理,并保证数据处理后满足识别所需的最小精度。传统的压缩感知(CS)算法在数据压缩和噪声去除方面[2]均可达到令人满意的效果,但其没有充分利用数据本身的稀疏与低秩结构[3]。低秩矩阵恢复(LRMR)是在压缩感知基础上发展起来的一种数据处理方法[4-5],主要由鲁棒主成分分析、矩阵补全和低秩表示等三类模型组成。它将CS向量样例的稀疏表示推广到矩阵的低秩情形,已成为继CS之后又一种重要的数据获取和表示方式。该方法注重探索数据内在规律及本质结构,考虑从较大但稀疏的误差中恢复出本质上低秩的数据矩阵。有时在不同的场合,低秩矩阵恢复也被称为矩阵低秩稀疏分解,即依据相关训练样本的类内信息对数据进行处理,将一个矩阵分解为一个低秩矩阵和一个稀疏矩阵之和的形式,再通过求解核范数优化问题来恢复低秩矩阵,这样可更好地保持数据结构,处理效率更高,恢复去噪效果更好[6]。

本文根据低秩矩阵恢复[7-8]的思想,提出基于低秩矩阵恢复理论的测井数据去噪方法,即将加速近端梯度[9-10](APG)算法和增广拉格朗日乘子[11](ALM)法应用于测井信号的去噪处理中,并对去噪后的测井数据分别采用支持向量机[12-13](SVM)和相关向量机[14](RVM)进行分类和识别,以期取得更为理想的测井效果。

1 基于低秩矩阵恢复的去噪方法研究

1.1 基于LRMR的去噪方法原理

假设矩阵D∈Rm×n由一个低秩矩阵A和一个稀疏噪声矩阵E组成,则LRMR可用如下优化问题来求解:

(1)

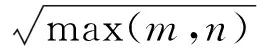
由于无法得到(1)式的闭合解,用凸优化方法得到增广拉格朗日函数:

(2)

式中,μ为常数。若μ大于0并接近于0,那么(2)式的解可近似为(1)式的解,记为:

(3)

(3)式是光滑的,并且具有李普希兹(Lipschitz)连续梯度,存在Lf>0,使得:

(4)

ALM算法[6]将本文的优化问题凸松弛到一个拉格朗日函数上,EALM算法每一步并不需要求出其子问题的精确解,而是交替地迭代矩阵A和E,直到满足终止条件为止。实际上,我们只需要更新A与E各一次得到子问题的一个近似解,就足以使算法最终收敛到原问题的最优解,从而得到一个更简洁且收敛更快的IALM算法。三种去噪算法的具体步骤分别如表1～表3所示。

1.2 基于LRMR的去噪方法流程

在样本分类过程中,大量噪声的存在会在很大程度上影响分类器的分类预测效果。为了提高去噪效果进而提高分类准确率,本文给出基于低秩矩阵恢复的去噪方法流程(图1)。

基于LRMR的去噪方法主要过程如下:

1) 输入待恢复去噪矩阵;

2) 设定APG,EALM,IALM三种算法的收敛条件和最大迭代次数,并调用三种算法进行低秩矩阵恢复去噪处理;

3) 对低秩矩阵恢复去噪后的结果进行输出。

表1 APG算法

表2 EALM算法

表3 IALM算法

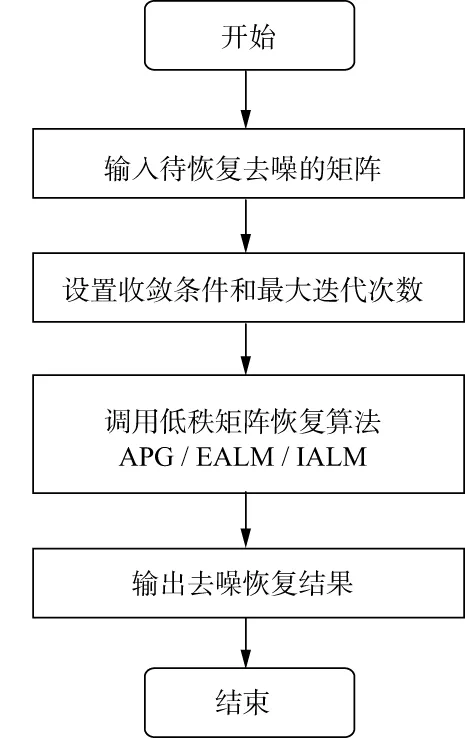
图1 基于LRMR的去噪方法流程

2 实际应用研究

油气层识别是石油勘测与开发的重要环节之一,是测井分析专家以及地质专家的研究重点。由于测井数据信息量巨大,样本空间复杂,以及极易受噪声的侵扰,因此,实际油气层识别难度很大。为解决大量噪声对油气层识别带来的困难,充分发挥测井数据的作用,我们用低秩矩阵恢复去噪算法APG/EALM/IALM进行测井数据去噪,并对去噪后的测井数据分别采用SVM/RVM进行油气层分类,以期取得令人满意的油气层识别效果。

2.1 油气层识别实现步骤

经低秩矩阵恢复去噪后的测井数据油气层识别模型如图2所示。

油气层识别的具体步骤如下:

1) 训练样本信息选取及样本信息的预处理。应尽量选取能够代表各深度特性的数据作为训练样本集,确保训练样本信息准确、全面、不重复。为了便于识别,还要将样本做归一化处理。待识别信息及测试样本在属性约简[15]后也要做归一化处理。

2) 样本信息属性约简。采用基于属性重要性的约简方法对训练样本进行属性约简。在识别过程中,待识别信息要按照训练样本属性约简后的结果剔除冗余属性。

3) SVM/RVM分类器建模。即将属性约简后的样本集作为输入信息,建立经典的高斯核SVM/RVM分类器模型。

4) 结果输出。通过分类器完成对油气层的识别,输出识别结果和识别效果图。

2.2 实际气层识别应用

某气田Su6井为低产、低含气丰度、大面积分布的隐蔽性岩性气藏。该气田测井得到的数据中不可避免地含有大量的冗余和噪声,利用常规的油气层识别方法对气层进行定量评价存在很大困难,因此采用APG/EALM/IALM三种算法进行了低秩矩阵恢复去噪处理。

Su6井研究深度800m,有13种测井属性,分别是自然伽马(GR)、声波时差(DT)、自然电位(SP)、微球聚焦(WQ)、深侧向电阻率(LLD)、浅侧向电阻率(LLS)、补偿密度(DEN)、补偿中子(NPHI)、光电吸收截面指数(PE)、铀(U)、钍(TH)、钾(K)、井径(CALI)。以0.125m为采样间隔(每米8个采样点)进行采样,所获测井数据共有6401个深度点,样本信息的决策属性为{非气层,气层}。令决策属性为D={d},d={di=i,i=0,1},其中0和1分别代表非气层和气层。对于条件属性的离散化处理采用基于曲线拐点的离散化算法[16]分别对每个属性各自单独离散化。首先将属性值由小到大排列,找出可能的拐点位置,然后根据一定的原则筛选出合适的离散点。对于经过离散化处理的样本决策表,采用差别矩阵约简法[17]约简为GR,DT,SP,LLD,LLS,DEN,K七个属性。另外,由于各种属性的量纲不一,数值范围各异,为避免建模计算中出现饱和现象,必须对样本数据进行归一化处理,使输入的样本数据大小在[0,1]之间。归一化公式如下:

图2 经过LRMR去噪后的油气层识别模型

(5)

其中,x∈[xmin,xmax],xmin,xmax分别为最小值和最大值。

为保密起见,本文只列出一部分归一化后的测井数据(表4)。图3为属性约减后7个属性在某井段之间的归一化曲线图,其中横轴表示深度(因保密需要,将实际井段深度做了平移),纵轴表示归一化的值。

对Su6气井数据进行了实际应用分析,运行环境基于Windows7操作系统平台,内存2.00GB,处理器为Intel Core i3 CPU,主频参数为2.30GHz。

2.2.1 支持向量机测井识别

分别采用APG,EALM和IALM算法对研究区测井数据进行低秩矩阵恢复去噪,运算过程中取最大迭代次数为10000,收敛条件为10-7。用经典的高斯核支持向量机进行分类,选取某关键井段的100个深度点作为训练样本集进行训练,并对恢复去噪之后的所有深度数据样本进行识别测试。为直观起见,对所有测井数据进行识别后,只取其中100个点来展示识别效果(图4)。图4a为直接对原始数据使用支持向量机识别的结果,图4b至图4d分别为经过APG,EALM和IALM低秩处理后支持向量机识别的结果。其中横坐标为选取的100个测试样本点,纵坐标为决策属性,“1”代表非气层,“2”代表气层,蓝色“○”表示实际分类标签,红色“*”表示识别结果,红色“*”和蓝色“○”不重合的点即为错分点。

表4 部分归一化测井数据

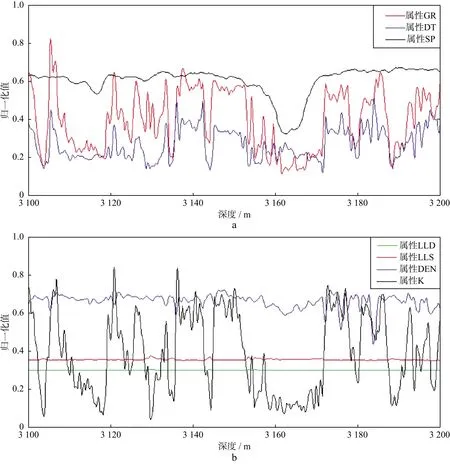
图3 经过归一化后的属性曲线a GR,DT,SP; b LLD,LLS,DEN,K

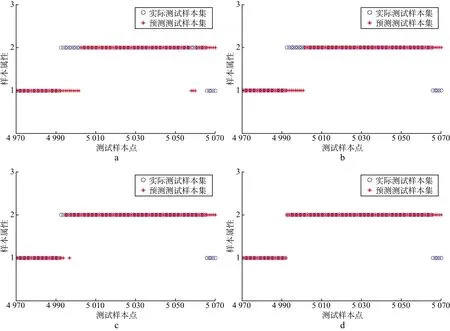
图4 支持向量机识别结果对比a 原始数据; b APG算法处理后; c EALM算法处理后; d IALM算法处理后

2.2.2 相关向量机测井识别

分别采用APG,EALM和IALM算法对研究区测井数据进行低秩矩阵恢复去噪,将Su6气井属性约减后的样本数据作为训练样本,用经典RVM模型进行训练,对恢复去噪后所有深度的测井数据进行识别测试。为直观起见,只取某关键井段100m来展示识别效果(图5)。图5a为直接对原始数据使用相关向量机识别的结果,图5b至图5d分别为经过APG,EALM和IALM低秩处理后相关向量机识别的结果。其中横坐标为选取的测井深度,纵坐标为决策属性,“0”代表非气层,“1”代表气层。

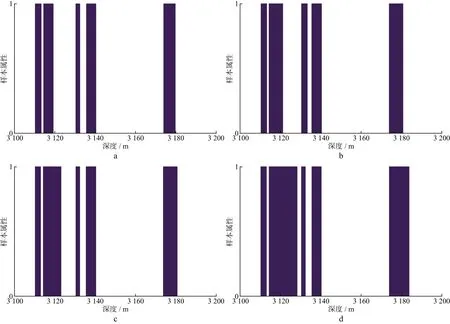
图5 相关向量机识别结果对比a 原始数据; b APG算法处理后; c EALM算法处理后; d IALM算法处理后

2.3 气层识别效果分析

表5展示了实际测井数据不同分类方法识别气层的性能指标。由表5可见,用APG,EALM和IALM算法对原始测井数据进行低秩矩阵恢复去噪后,支持向量机对气层的识别准确率分别为89.95%,90.30%,90.30%,相关向量机对气层的识别准确率分别为89.35%,90.15%和91.90%,相比去噪之前,识别准确率有了明显提升。由图5d可知,气层主要分布在3111～3113m,3115～3128m,3130.5～3131.5m,3136～3140m,3174～3183m井段(为保密起见,与实际井段有一个平移深度),识别结果符合实际测井情况。IALM算法在运算时间上明显优于EALM算法和APG算法。由此可知,在处理含有大量噪声的测井数据时,先进行低秩矩阵恢复去噪处理能有效提高分类效率和分类准确率,其中IALM算法对运算效率的提高最为明显。

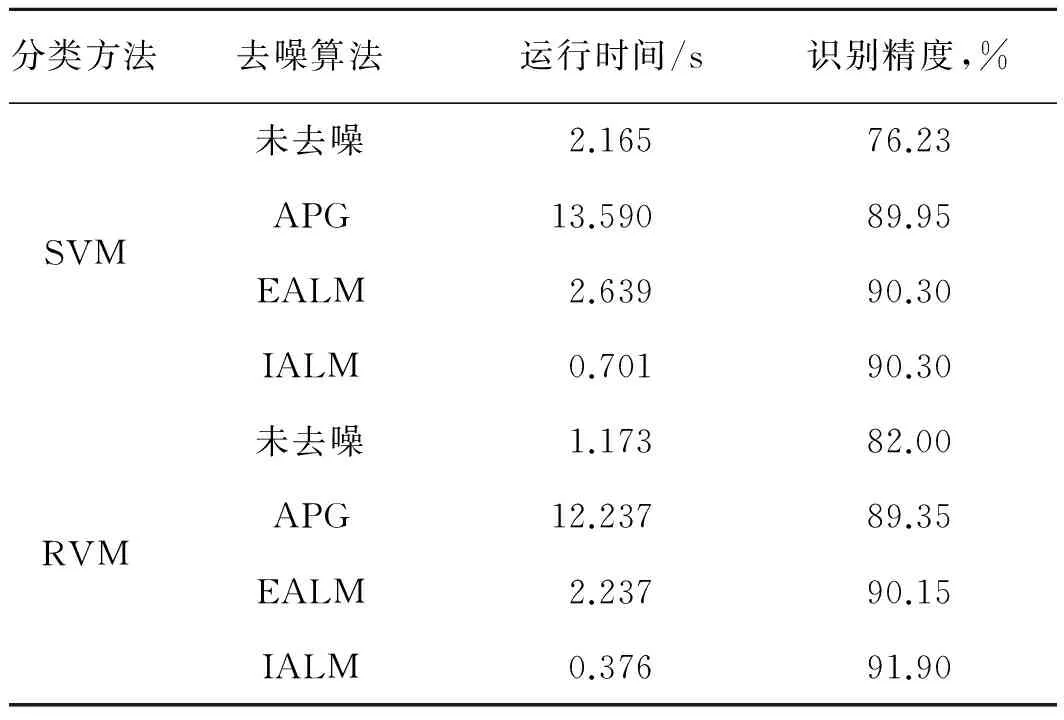
表5 测井数据不同分类方法性能指标对比

3 结束语

本文研究了低秩矩阵恢复去噪算法在石油测井中的应用,对APG,EALM和IALM算法的应用效果进行了对比。该方法充分利用了数据本身的稀疏与低秩结构,将传统压缩感知算法向量样例的稀疏表示推广到矩阵的低秩情形,使得数据处理更加高效和灵活。测井数据识别结果表明,IALM算法相比APG和EALM算法无论是气层分类的效率还是识别的精度都具有更好的效果。识别结果符合实际测井情况,在石油开发中具有重要意义。

[1] 陈钢花,张蕾,宋国奇,等.测井资料在确定不整合面深度中的应用[J].石油物探,2008,47(3):311-314 CHEN G H,ZHANG L,SONG G Q,et al.The application of well logging data in determined unconformity depth[J].Geophysical Prospecting for Petroleum,2008,47(3):311-314

[2] NIU W J,XIA K W,XIA X Y,et al.Logging data compression method based on sparse solution[J].Journal of Computational Information Systems,2014,10(19):8523-8530

[3] 张楠.低秩鉴别分析与回归分类方法研究[D].南京:南京理工大学,2012 ZHANG N.Low-rank representation based discrimination and regression based classification[D].Nanjing:Nanjing University of Science,2012

[4] 马坚伟,徐杰,鲍跃全,等.压缩感知及其应用:从稀疏约束到低秩约束优化[J].信号处理,2012,28(5):609-623 MA J W,XU J,BAO Y Q,et al.Compressive sensing and its application:from sparse to low-rank regularized optimization[J].Signal Processing,2012,28(5):609-623

[5] 于瑞国.维数约减算法研究及其在大规模文本数据挖掘中的应用[D].天津:天津大学,2008 YU R G.Research of dimensionality reduction and its application on data mining of large-scale text[D].Tianjin:Tianjin University,2008

[6] CANDES E J,TAO T.The power of convex relaxation:near-optimal matrix completion[J].IEEE Transactions on Information Theory,2010,56(5):2053-2080

[7] ZHOU Z H,WRIGHT J,CANDES E J,et al.Stable principal component pursuit[C]∥ Proceedings of 2010 IEEE International Symposium on Information Theory (ISIT).Austin,TX:IEEE Press,2010:1518-1522

[8] GANESH A,WRIGHT J,MA Y.Fast algorithms for recovering a corrupted low-rank matrix[C]∥ IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP).3rd ed.Aruba,Dutch Antilles:IEEE Press,2009:213-216

[9] TOH K C,YUN S.An accelerated proximal gradient algorithm for nuclear norm regularized least squares problems[J].Pacific Journal of Optimization,2010,6(11):615-640

[10] SHEN Y,WEN Z,ZHANG Y.Augmented lagrangian alternating direction method for matrix separation based on low-rank factorization[J].Optimization Methods and Software,2012,29(2):239-263

[11] VAPNIK V N.An overview of statistical learning theory[J].IEEE Transactions on Neural Networks,1999,10(5):988-999

[12] 刘得军,冉群英,王斌.支持向量机在大庆齐家凹陷测井解释中的应用[J].石油物探,2007,46(2):151-161 LIU D J,RAN Q Y,WANG B.The application of support vector machine in Daqing Qijia sag logging interpretation[J].Geophysical Prospecting for Petroleum,2007,46(2):151-161

[13] TIPPING M.Sparse Bayesian learning and the relevance vector machine[J].Machine Learning Research,2001,32(2):211-244

[14] CHEN D G,ZHAO S Y.Sample pair selection for attribute reduction with rough set[J].IEEE Transactions on Knowledge and Data Engineering,2012,24(11):2080-2093

[15] 夏克文,刘明霄,张志伟,等.基于属性相似度的属性约简算法[J].河北工业大学学报,2005,34(4):20-23 XIA K W,LIU M X,ZHANG Z W,et al.An approach to attribute reduction based on attribute similarity[J].Journal of Hebei University of Technology,2005,34(4):20-23

[16] 刘明霄.基于粗糙集的属性约简及其应用研究[D].天津:河北工业大学,2007 LIU M X.Study on attribute reduction based on rough set and its application[D].Tianjin:Hebei University of Technology,2007

[17] 夏克文,宋建平,李昌彪.基于粗集和神经网络的石油数据挖掘方法[J].信息与控制,2003,32(4):300-303 XIA K W,SONG J P,LI C B.An approach to oil log data mining based on rough set & neural network[J].Information and Control,2003,32(4):300-303

(编辑：戴春秋)

Adenoisingmethodbylow-rankmatrixrecoveryanditsapplicationinoilwelllogging

WANG Yanwei1,2,XIA Kewen1,2,NIU Wenjia1,2,Ali Ahamd1,2

(1.CollegeofElectronicsandInformationEngineering,HebeiUniversityofTechnology,Tianjin300401,China;2.KeylaboratoryofbigdatacomputationofHebeiprovince,Tianjin300401,China)

With the development of well logging techniques,the repository of data in the major oil fields has shown an enormous growth.Presence of redundancy and noise in well logging data requires the data to be compressed and denoised to make it useful for recognition of oil and gas layers.Low-rank matrix recovery (LRMR) theory generalizes the sparse representation of vector samples in compressed sensing (CS) to the matrix of low rank case.This theory considers recovery of the low-rank data matrix from large and sparse errors,leading to better maintenance of data structure and achieving a superior denoising effect.Thus,here we propose a denoising method through low-rank matrix recovery,and application of its three algorithms (accelerated proximal gradient (APG) algorithm,exact augmented Lagrange multiplier (EALM),and inexact augmented Lagrange multiplier (IALM)) to oil well logging data to improve the denoising effect.Pre- and post-denoising logging data were consequently used in oil and gas layer recognition by support vector machine (SVM) and relevance vector machine (RVM),respectively.Results show that oil and gas layer recognition accuracy is improved remarkably by the three denoising algorithms,compared to when denoising was not applied.IALM algorithm was superior to EALM and APG algorithms,through parameter optimization to reduce the number of iterations,which could obviously improve the operation efficiency.

oil well logging,data de-noising,low rank matrix recovery,accelerated proximal gradient (APG) algorithm,augmented Lagrange multiplier (EALM) algorithm

P631

：A

1000-1441(2017)05-0644-07DOI:10.3969/j.issn.1000-1441.2017.05.004

王艳伟,夏克文,牛文佳,等.基于低秩矩阵恢复的去噪方法在石油测井中的应用[J].石油物探,2017,56(5):650

WANG Yanwei,XIA Kewen,NIU Wenjia,et al.A denoising method by lowrank matrix recovery and its application in oil well logging

[J].Geophysical Prospecting for Petroleum,2017,56(5):650

2016-03-07;改回日期：2016-12-22。

王艳伟(1991—),女,硕士在读,研究方向为石油测井、大数据处理、数据挖掘等。

河北省自然科学基金(E2016202341)资助。

This research is financially supported by Hebei Province Natural Science Foundation (Grant No.E2016202341).