车装焊复合加工装备的服役可靠性评估

钟珂珂，付洋，金永乔，高通



车装焊复合加工装备的服役可靠性评估

钟珂珂1，付洋2，金永乔1，高通2

（1.上海航天精密机械研究所，上海 201600；2.西安电子科技大学 机电工程学院，西安 710071）

目的评估某型航天用车装焊复合加工装备在服役过程中的服役可靠性。方法首先分析装备常见的故障模式，统计装备在使用过程中的故障数据，由于装备故障数据样本量较少，所以提出基于贝叶斯理论的小样本车装焊复合加工装备可靠性评估方法，其中通过马尔科夫链蒙特卡罗(MCMC)法抽样解决贝叶斯理论中后验积分复杂的问题。结果确定了车装焊复合加工装备的寿命威布尔分布模型，并运用贝叶斯方法，计算出该车装焊复合加工装备的平均无故障工作时间(MTBF)。结论评估结果略低于设计要求，原因是目前该装备处于服役初期，服役初期故障数据较多。待进入稳定服役期时，故障率会有一定程度的降低后趋于稳定，MTBF会有一定幅度的增加，所以该车装焊复合加工装备MTBF基本满足设计要求。

服役可靠性评估；贝叶斯理论；MCMC方法；加工装备

数控机床作为现代制造业的重要装备，其可靠性指标是衡量一个国家制造水平的重要标志。车装焊复合加工装备是集成筒段铣削、箱底筒段精密装配、箱体环缝搅拌摩擦焊技术，用于生产运载火箭推进剂贮箱的一种制造装备。由于高品质的航天产品要求加工装备具有较高的可靠性，所以对该装备服役可靠性准确的评估对保障航天产品高品质要求具有重要的意义。

车装焊复合加工装备具有专业、非标准、特种加工等特点，这些特点也无疑增加了对其进行可靠性评估的难度。传统的数控装备可靠性评估方法是基于可靠性试验或服役过程中大量同型装备的故障统计数据，对数据进行拟合，选择拟合分布最好的模型，再利用大量故障统计数据对模型参数进行参数估计，评估机械装备的服役可靠性。常用方法有：最小二乘法[1-2]、极大似然估计法[3-5]、似然比检验法[6-7]等。

随着制造业的发展，满足某些特定加工的特种、定制数控加工装备越来越多，针对此类小样本情况下的数控装备可靠性评估技术还不够成熟。由于贝叶斯方法能够充分融合经验知识和装备的现场数据，有效解决小样本的问题，受到国内外学者的关注。王智明和杨建国[8]应用贝叶斯方法对二参数Weibull分布模型进行参数估计，给出了数控机床可靠性指标的区间估计和点估计。研究结果表明，针对此类故障数据样本量较少的可靠性分析问题中，应用贝叶斯方法优于极大似然估计法和似然比估计法。YANG等[9]将贝叶斯方法应用到数控机床的可靠性评估中，针对参数的先验分布的问题，提出融合多源先验信息的方法，有效地解决了小样本数控机床可靠性建模和评估的问题。于乃辉[10]以五轴联动加工中心为对象，采用信息融合的方法得到融合信息后的先验分布，再应用贝叶斯方法对二参数Weibull分布进行模型参数估计，对加工中心MTBF进行后验推断。彭卫文[11]以某型高速五坐标横梁移动龙门加工中心为研究对象，从全寿命周期的角度出发，分析、融合寿命周期各个阶段的可靠性数据和信息，随后应用贝叶斯方法，实现对数控机床可靠性的实时评估。除此之外，针对小样本的情况还有Bootstrap法[12]、支持向量机[13]等方法。

文中针对航天用车装焊复合加工装备评估其在服役过程中的可靠性，首先根据装备功能结构特点分析其故障模式，其次基于文献[8-11]的研究，将贝叶斯理论运用到该装备服役初期的可靠性评估中，提出了基于贝叶斯理论的车装焊复合加工装备可靠性评估方法。通过先验信息和观测信息的似然函数构建其后验分布，并通过MCMC方法来获得后验分布的估计，最终实现了对此装备的可靠性评估。

1 车装焊复合加工装备故障分析

车装焊复合加工装备是集成筒段铣削、箱底筒段精密装配、箱体环缝搅拌摩擦焊技术，用于生产运载火箭推进剂贮箱的一种制造装备。根据该装备的结构和功能特点，将该加工装备划分为夹具系统、支撑系统、执行机构、辅助系统和数控系统等5个部分，结构如图1所示。

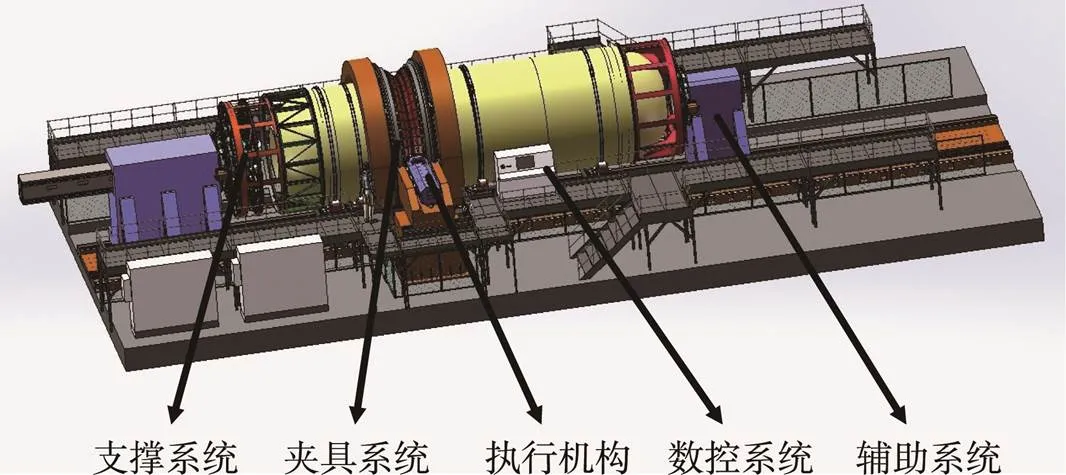
图1 车装焊复合加工装备结构

1.1 故障模式分析

故障模式分析的目的在于找出车装焊复合加工装备所有可能出现的故障模式，为可靠性分析奠定基础。对新型装备，一般可根据装备的功能原理和结构特点分析和预测装备可能出现的故障，或以与该装备具有相似功能、相似结构的装备所具有的故障模式为基础，分析装备的故障模式。

介于很多学者对数控装备的数控系统、主轴系统等进行了大量的研究，文中以车装焊复合加工装备代表性的环缝夹具系统为例进行了FMECA分析。环缝夹具用于工件焊缝的内撑外压，主要包含外夹具和内支撑两大部分，其中内支撑又分为固定式伺服内支撑和可拆卸式内支撑，结构如图2所示。经分析，确定该车装焊复合加工装备的夹具系统故障模式见表1。

图2 夹具系统结构

表1 夹具系统故障模式

1.2 故障数据

故障数据是装备可靠性(MTBF)评估的基础。本文根据《数控机床可靠性评定第1部分：总则》[14]国家标准，记录了车装焊复合加工装备在12个月内的故障数据，见表2。

表2 各部位发生故障次数及比例

2 基于贝叶斯理论的可靠性分析

贝叶斯理论基本思想是通过构造样本似然函数和验前信息，推导出其后验分布函数的表达形式，再利用可靠性试验数据作为样本数据来对概率密度函数或概率分布函数中的相关参数进行参数估计，最后得到各项可靠性指标的估计值。

车装焊复合加工装备故障间隔时间服从Weibull分布，针对两参数Weibull分布，其概率密度函数为：

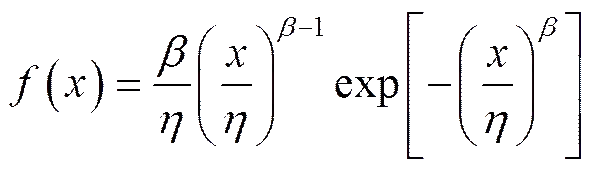
式中：，分别为二参数威布尔分布的形状和尺度参数，均大于0。

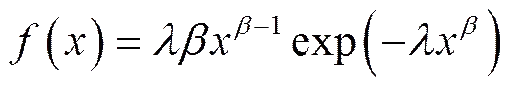
其不可靠度函数（寿命分布函数）为：

(3)

根据贝叶斯理论，其寿命模型的后验分布表达式可写为：

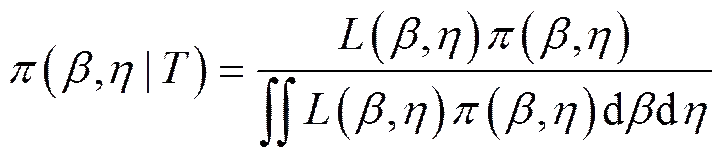
式中：()为故障样本数据似然函数；()为二参数Weibull分布参数联合先验分布。

各参数的贝叶斯估计为：

(6)

MTBF的贝叶斯估计为：

2.1 样本似然函数构建

对车装焊加工装备运行状态和相关故障情况进行记录，可得到关于该装备的现场运行故障数据。根据故障间隔时间（寿命）观测值构建其似然函数为：

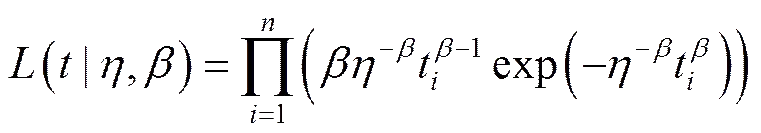
2.2 后验分布的确立

Weibull分布形状参数参数有较为明显的物理意义，对于无故障工作时间服从Weibull分布的数控机床来说，当形状参数分别大于1、等于1和小于1时，表明故障分别处于损耗失效区、偶然失效区和早期失效区。由于该数控装备处于调试阶段即早期失效期，故采用先验分布() ~(0,1)。尺度参数的先验信息由相似机床MTBF提供，采用先验分布()~(400,500)，则参数和的联合先验分布为：

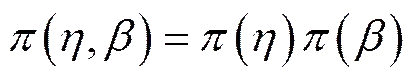
由贝叶斯公式得到后验分布：

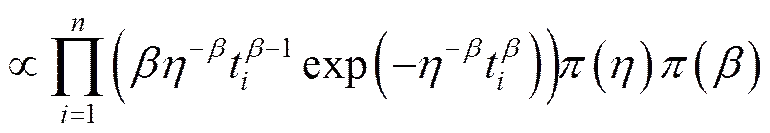
由于其后验分布(,|)高维复杂，积分困难，有时甚至无法积分。可以利用MCMC思想对后验分布进行模拟求解。

MCMC是一种将马尔可夫过程引入到蒙特卡罗模拟中的特殊的蒙特卡罗方法，其本质上是利用马尔可夫链的蒙特卡罗积分。基本思想是：通过建立马尔可夫链对未知变量进行大量的抽样模拟，当马尔可夫链达到稳态分布时即可获得所求参数的后验分布。在此基础上，利用稳态分布中大量的抽样点来近似计算蒙特卡罗积分。以此在不需要对后验分布函数进行计算的情况下来保证贝叶斯方法的有效实施。

2.3 贝叶斯分析中MCMC的计算

在贝叶斯分析中，设维随机向量(1,2,…,θ)具有联合分布(1,2,…,θ)，其中，θ(=1, 2,…,)为模型参数或缺失的观测值，(·)为其后验分布。则函数()的后验数学期望为：

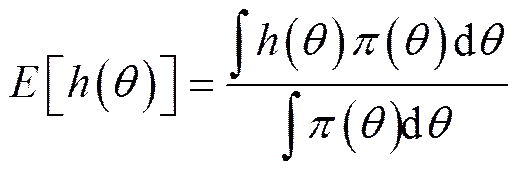
由于式（11）中的积分通常情况下形式过于复杂难以计算，因此采用MCMC稳态模拟方法进行近似模拟计算。在上构建转移核为(·,·)的马尔科夫链，使其平稳分布为()；由中的某一点(0)出发，利用前步中的马尔科夫链生成序列(1),(2),…,(n)；在估计[()]时应将前面个预迭代值去掉，即：

(12)

2.4 基于MCMC的后验抽样

Gibbs抽样过程采用分而治之思想，即在推断一组参数过程中，假设其他参数固定不变且己知。令θ代表某种随机变量或同组的几个随机变量，第组变量的边际分布为(θ)。Gibbs抽样法从()中抽样的步骤如下：给定任意初始向量；从条件分布中抽取样本，从中抽取样本；从抽取样本；从抽取样本；至此即完成了由到的一次转移，为马尔科夫链的一次实现值；经过次迭代，得到，并最终得到马尔科夫链：。

2.5 基于BUGS的建模分析

BUGS软件是利用Gibbs抽样法实现MCMC方法的贝叶斯推断专用软件包。在BUGS软件中建立二参数Weibull分布的Doodle模型，代入寿命数据进行参数估计，截取前1 000次抽样结果，从1 001开始进行20 000次抽样统计，参数估计结果见表3，迭代过程及后验抽样密度如图3所示。

表3 参数后验估计统计量

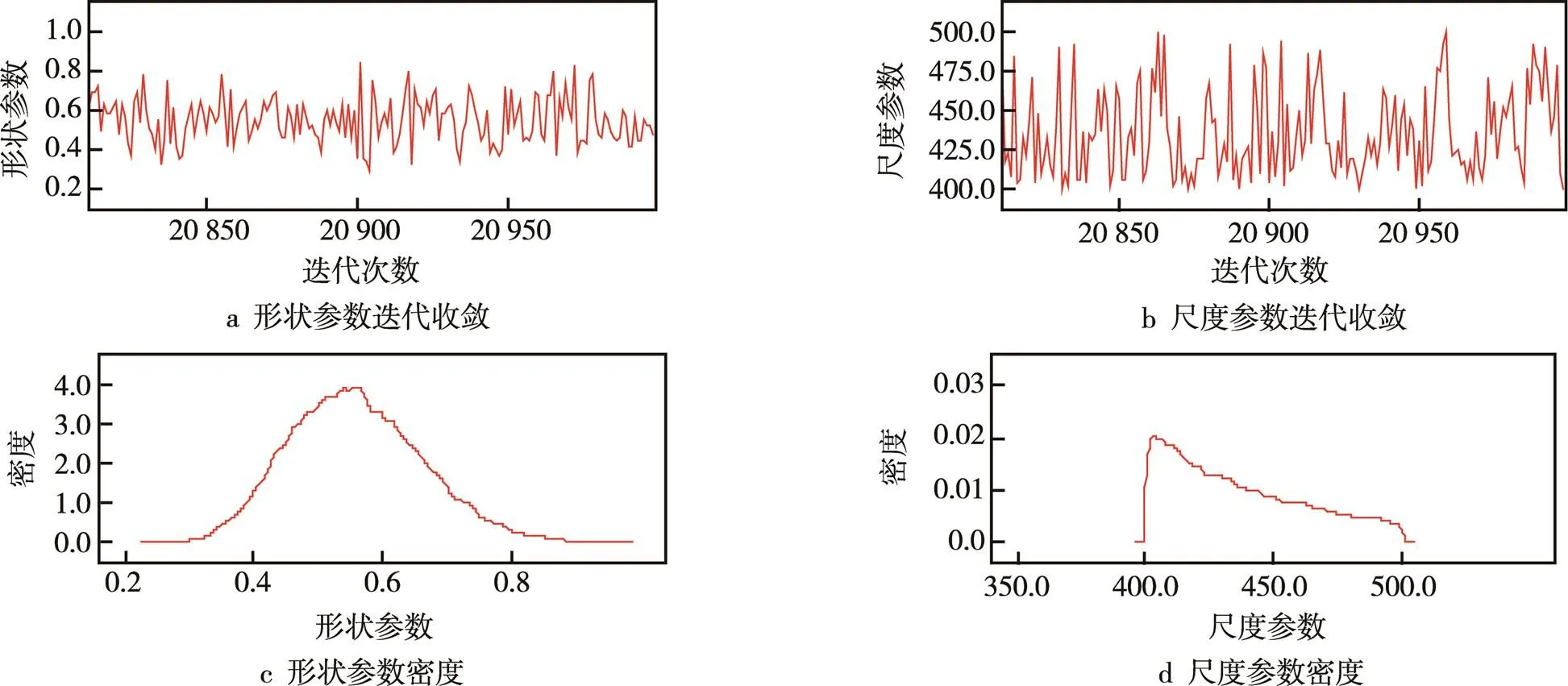
图3 参数迭代过程及后验抽样密度

取贝叶斯后验均值作为各参数的估计值，根据上述计算方法，车装焊复合加工装备平均无故障工作时间为724 h，而该装备MTBF设计为800 h。原因是目前该装备处于服役初期，由浴盆曲线可知，服役初期故障率较高，待进入稳定服役期时，故障率会有一定程度降低后趋于稳定，MTBF会有一定幅度的增加，所以该装备基本满足可靠性设计要求。

3 结论

该研究从车装焊一体化数控复合加工装备的故障模式分析入手，结合服役初期现场故障数据，通过基于马尔科夫链稳态模拟的贝叶斯方法，最终实现了对该装备可靠性的评估，得到如下结论：

1）该研究跟踪采集1年的现场故障数据，按照可靠性评估要求的故障计数原则对数据进行预处理，并结合装备功能原理、结构特点，以夹具系统为例，分析了该装备的故障模式，为之后的可靠性评估奠定基础。

2）针对贝叶斯理论后验分布高维数值积分问题，提出马尔科夫链稳态模拟方法，对后验分布进行模拟抽样，有效地解决了贝叶斯后验积分问题。

3）该装备MTBF设计要求800 h左右，评估结果略低于设计要求。原因是目前该装备处于服役初期，服役初期故障率较高，待进入稳定服役期时，故障率会有一定程度的降低后趋于稳定，MTBF会有一定幅度的增加，所以该装备基本满足设计要求。

[1] 王汉伟. 意大利蓝苞蒂五轴联动加工中心可靠性综合评价研究[D]. 长春: 吉林大学, 2013.

[2] WANG Yi-qiang, JIA Ya-zhou, JIANG Wei-wei. Early Failure Analysis of Machining Centers: A Case Study[J]. Reliability Engineering & System Safety, 2001, 72(1): 91- 97.

[3] 王智明, 杨建国, 王国强, 等. 多台数控机床的时间截尾可靠性评估[J]. 哈尔滨工业大学学报, 2011(3): 85- 89.

[4] DAI Yi, ZHOU Yun-fei, JIA Ya-zhou. Distribution of Time between Failures of Machining Center Based on Type I Censored Data[J]. Reliability Engineering & System Safety, 2003, 79(3): 377-379.

[5] 黄雷. 加工中心可靠性研究[D]. 沈阳: 东北大学, 2009.

[6] 杨建国, 王智明, 王国强, 等. 数控机床可靠性指标的似然比检验区间估计[J]. 机械工程学报, 2012(2): 9-15.

[7] 张根保, 李冬英, 刘杰, 等. 面向不完全维修的数控机床可靠性评估[J]. 机械工程学报, 2013(23): 136-141.

[8] 王智明, 杨建国. 少样本故障数据数控机床的贝叶斯可靠性分析[J]. 中南大学学报(自然科学版), 2014(12): 4201-4205.

[9] YANG Zhao-jun, KAN Ying-nan, CHEN Fei, et al. Bayesian Reliability Modeling and Assessment Solution for NC Machine Tools under Small-sample Data[J]. Chinese Journal of Mechanical Engineering, 2015, 28(6): 1229- 1239.

[10] 于乃辉. 五轴联动加工中心可靠性试验与评估方法研究[D]. 长沙: 国防科学技术大学, 2011.

[11] 彭卫文. 高速五坐标横梁移动龙门加工中心可靠性评估技术研究[D]. 西安: 电子科技大学, 2012.

[12] 徐玉茗, 邓超, 吴军. 基于Bootstrap方法的可靠性评估[J]. 机械设计与制造, 2010(3): 105-107.

[13] 徐玉茗, 邓超. 基于支持向量机和Bayes方法的机械系统可靠性综合方法[J]. 机械设计与制造, 2010(5): 212-214.

[14] GB/T 23567.1—2009, 数控机床可靠性评定第1部分:总则[S].

Operational Reliability Evaluation of Turning-assembly-welding Composite Machining Equipment

ZHONG Ke-ke1, FU Yang2, JIN Yong-qiao1, GAO Tong2

(1.Shanghai Spaceflight Precision Machinery Institute, Shanghai 201600, China; 2.School of Mechano-Electronic Engineering, Xidian University, Xi’an 710071, China)

Objective To evaluate the operational reliability of a certain type of aerospace turning-assembly-welding composite machining equipment in the operational process. Methods At first, common failure modes of the equipment were studied and its failure data was obtained during operational process. Then, the reliability evaluation model of the turning-assembly-welding composite machining equipment using the Bayesian method was proposed with small-sized sample failure data. The complex problem on Posterior integration in Bayesian theory was solved by the Markov Chain Monte Carlo (MCMC) theory. Results The lifetime Weibull distribution of turning-assembly-welding composite machining equipment was determined. Furthermore, the mean time between failures (MTBF) of turning-assembly-welding composite machining equipment was calculated based on the Bayesian method. Conclusion The evaluation result is slightly lower than that of the design. The main reason is that more failure data appeared in the early operational process. The failure rate will decrease and the MTBF will increase in the stable operational process. So the MTBF of the machining equipment basically meets the design requirement.

operational reliability evaluation; Bayesian theory; MCMC method; machining equipment

10.7643/ issn.1672-9242.2017.09.020

TJ07；TH113

A

1672-9242(2017)09-0099-05

2017-04-22；

2017-05-27

高档数控机床与基础制造装备国家科技重大专项（2013ZX04001101）

钟珂珂（1987—），男，上海人，硕士，工程师，主要研究方向：航天机电设备数据采集与故障诊断、复杂机电系统可靠性评估。