等效阵长对声压线阵声呐空间增益的影响分析

王 森，王 余，王易川，高 鑫

(1. 海军潜艇学院，山东 青岛 266000；2. 中国人民解放军31001部队，北京 100000)

等效阵长对声压线阵声呐空间增益的影响分析

王 森1，王 余2，王易川1，高 鑫1

(1. 海军潜艇学院，山东 青岛 266000；2. 中国人民解放军31001部队，北京 100000)

为了研究声压线阵声呐空间增益的影响因素，就同等阵元个数情况下线阵声呐等效阵长与波束形成结果的关系进行仿真分析。首先，建立了直线阵、圆阵、半圆阵和太极阵的声压线阵声呐模型，定义了线阵声呐等效阵长的数学表达式，对线阵声呐等效阵长的进行了对比分析。其次，引入“–3dB波束宽度”概念，通过蒙特卡罗试验，得出了线阵声呐等效阵长与“–3dB波束宽度”之间的反比关系。最后，对多目标情况下的波束形成仿真结果进行对比分析，验证了等效阵长对线阵声呐空间增益的影响关系。

声压线阵声呐；等效阵长；半圆阵；波束宽度

0 引 言

声压线阵声呐是一种经典的声呐类型，由若干个声压水听器按照一定规律布放成阵，通过波束形成（Beam forming）来提高系统增益，依靠被动方式实时获取声场中的声能流信息，进而得到观测目标的方位信息及特征参数。

自问世以来，线阵声呐就被广泛应用于水声测量领域。单就声呐布阵方式而言，线阵声呐就包括直线阵、圆阵、半圆阵和太极阵等。直线阵声呐是一种基础的声呐阵型，由等间距布放的声压水听器组成，其观测场呈圆柱状对称，存在左右舷模糊现象[1]。圆阵[2-3]、半圆阵和太极阵[4]声呐则克服了直线阵自身的“圆柱状对称问题”，避免了左右舷模糊问题的发生。线阵声呐的布放使用是一项庞杂的系统工程，声呐的布阵方式及阵元的布放数量都对布阵效果起着决定性作用。因此，对于某个阵元个数一定的等间距线阵来说，如何合理选择布阵方式来实现最优的声呐空间增益就显得尤为重要。

本文针对等间距线阵声呐的空间增益问题开展研究，比较了直线阵、圆阵、半圆阵和太极阵的线阵声呐模型，就4种线阵声呐的等效阵长进行对比分析，得出了线阵声呐等效阵长与其波束形成空间增益性能的关系，并通过仿真分析对结论进行验证。

1 线阵声呐模型

1.1 直线阵

直线阵是一种常用的线阵声呐布阵方式。假设直线阵声呐阵元个数为N，阵元间距为dm，信号入射方向与所在轴线的夹角为θ。则该直线阵声呐模型如图1所示。

1.2 圆阵

圆阵是一种声压水听器按圆形均匀分布的布阵方式。假设圆阵声呐阵元个数为N，阵元间的弧长间距为d，圆阵半径为r，信号入射方向与圆阵坐标横轴轴线夹角为θ。则该圆阵声呐模型如图2所示。

1.3 半圆阵

半圆阵是一种声压水听器按半圆形（即圆心角为180°的圆弧）均匀分布的布阵方式。假设半圆阵声呐阵元个数为N，阵元间的弧长间距为d，半圆阵半径为r，信号入射方向与半圆阵坐标横轴轴线夹角为θ。则该半圆阵声呐模型如图3所示。

1.4 太极阵

太极阵是一种声压水听器按2个等尺寸逆向半圆形均匀分布的布阵方式。其阵型形状近似“太极”型，所以称作“太极阵”。假设太极阵声呐阵元个数为N，阵元间的弧长间距为d，半圆型的半径为r，信号入射方向与太极阵坐标横轴轴线夹角为θ。声呐模型如图4所示。

2 等效阵长

2.1 坐标系

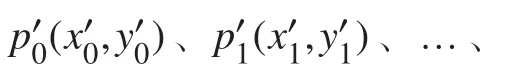
2.2 阵型比较

根据图5所示坐标系，将直线阵、圆阵、半圆阵和太极阵4种线阵声呐进行阵型对比分析，如图6所示。4种线阵声呐阵元个数均为40，阵元间距（或阵元间的弧长间距）为3 m。根据弧长与半径的几何关系可得：圆阵和太极阵的半径为18.14 m，半圆阵的半径为36.28 m。

通过图6可以看出，就直线阵法线方向而言，直线阵具有最大的声呐接收孔径l（l=Nd=2πr），半圆阵和太极阵为4r，圆阵仅为2r；就直线阵所在轴线方向而言，圆阵、半圆阵和太极阵的接收孔径均为2r，而直线阵则趋近于0。

2.3 等效阵长的计算

为了对4种声压线阵各方向的声呐接收孔径进行定量分析，需要计算其各自的等效阵长。在图5所示坐标系中，等效阵长LE可以定义为：

可以看出，等效阵长即线阵在波束形成方位垂线上的最大投影长度，可以反映在当前方位进行波束形成的有效阵元数量和孔径。根据式（1）计算4种声压线阵声呐的等效阵长，结果如图7所示。

通过图7可以看出，随着波束形成方位角度的变化，直线阵等效阵长的变化幅度为（0，120]，在90°和270°方位取得最大值120；圆阵等效阵长恒为直径，即36.28；半圆阵等效阵长变化幅度为[36.28，72.56]，在90°和270°方位取得最大值72.56；太极阵等效阵长的变化幅度为[24.35，72.56]，在90°和270°方位取得最大值72.56，但方位为22°和202°时取得最小值24.35。

3 空间增益分析

3.1 波束形成

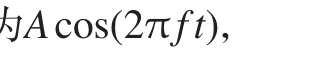
其中：

归一化的指向性函数为：

对4种声压线阵声呐进行仿真分析，仿真信号采用高斯白噪声，信号频段为200～300 Hz，声速为1 500 m/s。假设信号入射方向分别为0°、45°和90°，波束形成结果如图8～图10所示。

从图8～图10可以看出，当信号入射方位为0°时，直线阵的方位分辨能力较差；当信号入射为45°和90°时，直线阵出现左右舷模糊，在不存在左右舷模糊的3种阵型中，半圆阵的方位分辨能力最佳。

3.2 波束宽度

在声呐的波束形成结果分析处理中，“–3 dB波束宽度”与目标的直观辨识度关联紧密，可以较好地反应线阵声呐的波束形成空间增益效果和对入射目标信号的分辨能力。

根据式（6）对4种声压线阵声呐进行仿真分析，对比不同入射方位情况下各阵型的波束宽度。考虑到太极阵等效阵长的变化情况，选择22°、90°和180°三个特定方位进行仿真并计算各阵型的波束宽度，结果如图11～图13和表1所示。

通过仿真计算，结合各阵型的等效阵长（见图7）可以看出，直线阵在方位90°时的等效阵长最大，对应的波束宽度最小，方位180°时的等效阵长最小，对应的波束宽度最大；圆阵由于自身的全方位对称性，等效阵长不随方位的变化而改变，对应的波束宽度变化也较小；半圆阵和太极阵在90°方位时等效阵长是圆阵的2倍，对应的波束宽度也约是圆阵的一半，在180°方位时二者与圆阵的等效阵长相当，对应的波束宽度也近似相等；太极阵在方位22°时的等效阵长最小，对应该方位的波束宽度最大。

考虑到高斯白噪声的随机性，任一类型的线性声呐在同方位的空间增益也会存在差异，这些差异会影响等效阵长与波束宽度的线性对应关系。因此，为了对线阵声呐波束形成后的空间增益问题进一步分析，本文采用蒙特卡罗试验，对0°～360°的各入射方位进行仿真分析，并绘制4种线阵声呐各方位的–3 dB波束宽度变化曲线如图14和图15所示。

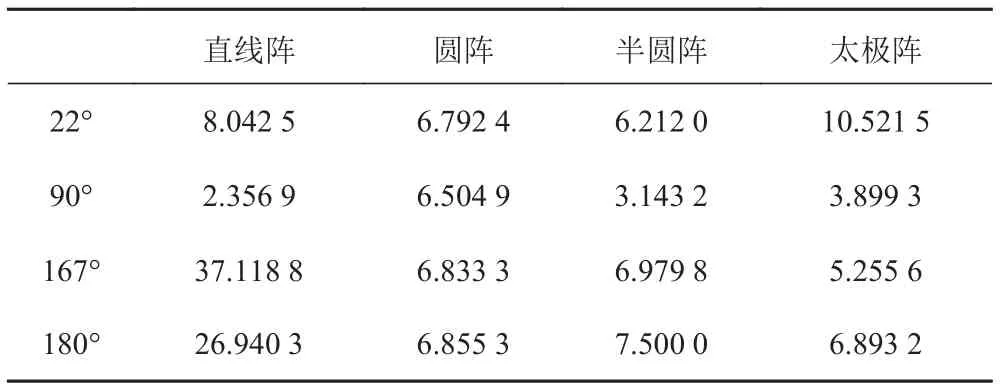
表 1 波束宽度比较Tab. 1 Comparison of beam width

通过对比图7、图14和图15可以看出，圆阵、半圆阵和太极阵声呐的–3 dB波束宽度与等效阵长存在线性变化关系；直线阵在0°～13°、167°～193°和347°～360°三个方位区间内的波束宽度存在突变。考虑到空间方位的对称性，选取167°的目标方位进行空间增益分析，如图16所示。可以看出，由于直线阵自身的左右舷模糊缺陷，–3 dB波束宽度计算过程中受到模糊源伪瓣干扰，造成波束宽度数值的突变。将受到左右舷模糊的方位区间排除后，直线阵声呐的等效阵长与–3 dB波束宽度之间也存在较好的反比关系。

3.3 多目标仿真

对4种声呐线阵进行多目标仿真分析，仿真信号采用高斯白噪声，信号频段为200～300 Hz，声速为1 500 m/s。仿真时长为1 200 s，目标数量为8，各目标在仿真时段内的方位变化分别为9°～232°，73°～47°，100°～95°，174°～186°，195°～168°，234°～268°，241°～281°和313°～351°。仿真结果如图17～图20所示。

通过对比可以看出，直线阵声呐存在左右舷模糊，难以区分目标的真实方位，在0°和180°方位附近的方位分辨能力较差；圆阵、半圆阵和太极阵均不存在左右舷模糊现象，圆阵在各个方位具有相同的方位分辨能力，半圆阵在0°和180°方位附近的方位分辨能力与圆阵相当，且在90°和270°方位附近优于圆阵，但太极阵在22°和202°方位附近的方位分辨能力较差。

4 结 语

本文针对等间距线阵声呐的空间增益影响因素，对比分析了直线阵、圆阵、半圆阵和太极阵的线阵声呐模型，研究了等效阵长与方位分辨能力的关系，得出了如下结论：

1）线阵声呐的等效阵长与波束宽度之间具有反比关系，即某个方位的等效阵长越大，波束形成后的波束宽度越窄，方位分辨能力越强。

2）同等阵元个数情况下，半圆阵线阵声呐既不存在直线阵的左右舷模糊问题，又具有优于圆阵和太极阵的方位分辨能力，空间增益性能最佳。

[1]韩树平, 许兆鹏, 董永峰. 长线阵声纳左右舷分辨仿真研究[J].计算机仿真, 2012, 29(11): 412–415.HAN Shu-ping, XU Zhao-peng, DONG Yong-feng. Research on simulation of long towed line array’s port/starboard discrimination[J]. Computer Simulation, 2012, 29(11): 412–415.

[2]郭伟. 水下监测系统中目标探测若干关键技术研究[D]. 长沙:国防科学技术大学. 2011.GUO Wei. Research on key methods of target detecting for underwater monitoring system[D]. Changsha: National University of Defense Technology. 2011.

[3]朱丽华. 基于均匀圆阵的DOA算法研究[D]. 石家庄: 河北科技大学. 2014.ZHU Li-hua. Research on DOA algorithm based on uniform circular array[D]. Shijiazhuang: Hebei University of Science and Technology. 2014.

[4]WANG Sen, LI Zhi-zhong, DAI Wei-guo, et al. The simulating calculation of left/right ambiguity based on scalar tai-ji array[C]// IEEE ICCSN. 2017.

[5]李启虎. 声呐信号处理引论[M]. 北京: 科学出版社, 2012.LI Qi-hu. An introduction to sonar signal processing[M].Beijing: Science Press, 2012.

[6]任鹏飞, 张玉, 邓小波. 一种基于Y阵的MUSIC波达方向估计算法[J]. 无线电工程, 2014, 44(3): 54–56.REN Peng-fei, ZHANG Yu, DENG Xiao-bo. MUSIC DOA estimation algorithm based on Y-shaped array[J]. Radio Engineering, 2014, 44(3): 54–56.

[7]张虎, 仝侨. 基于L型阵的二维Root-MUSIC波达方向估计算法[J]. 电子科技, 2015, 28(2): 11–13.ZHANG Hu, TONG Qiao. Two-dimensional Root-MUSIC direction estimation based on an L-shaped array[J]. Electronic Science and Technology, 2015, 28(2): 11–13.

[8]李子高, 李淑秋, 闻疏琳. 一种基于独立成分分析的水下宽带信号波达方位估计方法[J]. 兵工学报, 2017, 38(1): 114–122.LI Zi-gao, LI Shu-qiu, WEN Shu-lin. A novel ICA-based DOA estimation method for underwater wideband source[J]. ACTA ARMAMENTARII, 2017, 38(1): 114–122.

[9]WANG Sen, DAI Wei-guo, LI Hai-tao. Spatial gain research of complex towed array sonar distortion[C]// IEEE ICFST 2017.

Impact analysis of equivalent array length on spatial gain of pressure hydrophone array sonar

WANG Sen1, WANG Yu2, WANG Yi-chuan1, GAO Xin1
(1. Navy Submarine Academy, Qingdao 266000, China; 2. No. 31001 Unit of PLA, Beijing 100000, China)

The simulation analysis of relationship between beam forming results and equivalent array length of array sonar has been done, in order to study the factors that influence spatial gain of pressure hydrophone array sonar with a fixed number of arrays. Firstly, the array sonar models of linear array, circle array, semicircular array and tai-ji array have been established. The mathematical expression of equivalent array length is defined and the comparison has been done. Secondly,the conception of –3 dB beam width is defined. The inverse relationship between equivalent array length and –3 dB beam width is obtained through the Monte-Carlo experiments. Finally, the results of beam forming simulation with multiple objective are contrasted and the relationship between spatial gain and equivalent array length is affirmed.

pressure hydrophone array sonar；equivalent array length；semicircular array；beam width

TB56

A

1672 – 7649(2017)09 – 0123 – 06

10.3404/j.issn.1672 – 7649.2017.09.024

2017 – 05 – 10

王森(1988 – )，男，博士研究生，研究方向为水声目标识别、水声信号处理。