维数约简算法简述

马发民+张林+王锦彪

摘 要：机器学习是近几年研究的热点，维数约简算法是机器学习的必要手段，本文从维数约简算法的定义讲起，介绍了几种典型的数据降维算法，其中包括线性降维和非线性降维，流形学习是非线性降维的代表算法。并且介绍了每个算法的构造过程及其特点，在此基础上分析了所有维数约简算法的执行效率时间和空间复杂度，并且给出了每个算法的特点和算法的核心思想，最后在此基础上给予总结，为后面研究者提供参考和借鉴。

关键词：机器学习；维数约简；数据降维；线性降维；非线性降维

中图分类号：TP301 文献标识码：A

Abstract：Machine learning，mainly realized through dimensionality reduction，has become a hot topic for research in recent years.This paper first presents the definition of the dimensionality reduction algorithm，and then introduces several typical data dimensionality reduction algorithms including linear dimensionality reduction and non-linear dimensionality reduction（manifold learning is the typical algorithm of non-linear dimensionality reduction）.Besides，the paper elaborates on the construction process and characteristics of each algorithm，then analyzes the execution efficiency time and space complexity of all dimensionality reduction algorithms and provides the features and key point of each algorithm.Most importantly，the final conclusion offers references to future researchers.

Keywords：machine learning；dimensionality reduction；data dimensionality reduction；linear dimensionality reduction；

non-linear dimensionality reduction；manifold learning

1 引言（Introduction）

機器学习是近几年比较火的一个研究方向，不论在模式识别还是图像处理方面都要用到机器学习的理论，机器学习中有个重要的方面研究就是如何把大数据量内容降低成有限的维数，从而提高机器学习的速度，这里面用到一个关键的算法就是维数约简算法，它的原理就是通过线性和非线性的方法，将高维数据降低到可以解的低维数据从而提高机器学习的速度。接下来文章将从维数约简数学定义说起，紧接着介绍常用的几种维数约简算法，并且给出这些算法的优缺点，最后给出总结为后续做研究的人提供指引和方向。

2 维数约简数学定义（Mathematical definition of

dimensionality reduction）

定义1：给定个数据点，

，。

构造映射，其中

，即

我们把叫作低维表示方法。

假如映射F是线性的那么这种降维叫作线性降维，同理若F是非线性的则这种降维叫作非线性降维。

定义2：构造这样一个映射其中，那么我们由此可以推导出，而我们把这种映射称为嵌入映射。

定义3：拓扑空间[1]

这种空间是这样一种形式的数对，而X和都是集合这种集合所具备的特点是：

（1）集合的元素是无穷多且这些元素没有边界；

（2）并且它们的交集也是没有边界的；

（3）那么我们把这样的集合数对称为拓扑空间。

定义4：Hausdorff空间[1]

若对于空间中的任意的，存在的邻域 和的邻域，使，则称为一个Hausdorff空间。

定义5：流形[1]

设是一个Hausdorff空间，如果对任意的一点，都有的一个开邻域与的某个开子集同胚，则称是维拓扑流形，简称维流形。

定义6：流形学习[2]

对于数据集，如果存在，

并且它是维数较低的流形，存在，其中，对于通过映射到低维空间，流形学习的含义就是将数据集X降低维数，同时根据构造函数找出其所对应的坐标，这样的过程就是流形学习，日常的一些较大数据的降维都是通过流形学习来实现的。

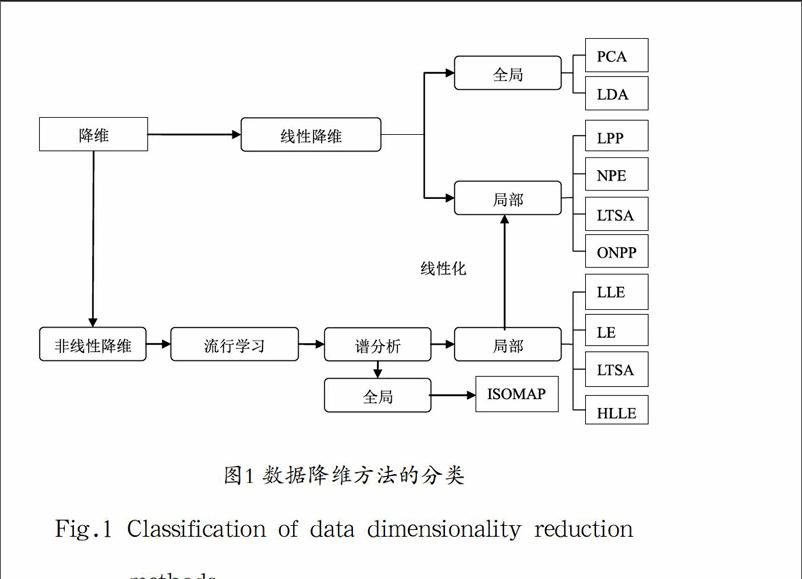
维数约简算法是机器学习的重要组成部分，且方法众多，不同的角度和使用方法，它们又有不同的分类，但是有种分类是较常用的且被大多数人所接受，这种分类方法如图1所示。

3 典型的线性降维算法（A typical linear

dimensionality reduction algorithm）

3.1 主成分分析法

主成分分析法顾名思义就是从众多因素中提取出来主要成分即几个关键因素，通过这几种关键因素的分析出整个数据的特点[3]，需要注意的是当我们提取出的关键特征，这些特征能够代表整个数据的特点，即可以通过这些特征线性的表示出整个数据的特征，这有点像唯物辩证法中的通过事物的表象看到事物的本质，或者是根本矛盾决定一般矛盾，由于该方法提出时间较早[4]，且操作起来简单并且降维后的结果较好因此广泛地被人们用于维数约简中。endprint

考虑点集

令

对谱分解

（1）

其中，，为对角阵，并且，，为对应的特征向量，主成分按照式（2）变换得到

（2）

3.2 多维尺度变换

高维数据在数据空间中通常具有如下特点，数据间存在一定的距离和相似性[5]，正如数据在高维空间具备一定的拓扑关系，而这种关系通常表现在数据之间的距离和相似性，而为了保持数据的这些特点将高维的数据降低到有限维的二三维空间准中，我们把这种降维的方法叫作多维尺度变换，根据变换时保留原始数据之间的特点不同，又分为度量和非度量的多维尺度变换[6]，具体变换方法如下：

假设数据集，其中单个样本点为，其中，为样本点个数，为样本点维数，设所有样本组成的维矩阵为，样本间两两内积组成的矩阵为。

样本与之间欧氏距离为

（3）

距离矩阵为

（4）

其中，，。

定义中心化矩阵：。对距离矩阵双中心化有

（5）

设

对做特征值分解：

设为从大到小排列的特征值，为对应的特征向量，取前个特征值和对应的特征向量得到低维表示为

（6）

下面给出输出求A的幂集P（A）的另一种递归算法：

（1）若n=0，P（A）={}，输出空集；

（2）若n>1，

输出A中的一个元素an后，求集合A-an={a1，a2，…，an-1}的幂集输出，并将A-an={a1，a2，…，an-1}的幂集的每一个元素与an并起来输出。

4 非线性降维（Nonlinear dimensionality reduction）

4.1 等距映射算法

Tenenbaum J B等人在2000年提出了Isomap算法[7，8]，此算法与多维尺度变换有些类似，多维尺度主要考虑数据间是有距离的而这种距离也称为欧式距离，在此基础上提出了等距离映射算法，该算法首先需要计算出数据间的最短距离，用临近路径二维表表示，将最短距离转化为测地线距离，进而将高维数据降为低维数据，具体的转换构造方法如下：

（1）构造局部邻域。计算每个样本点的近邻点集合，一般采用近邻或邻域法。近邻法就是找出离点最近的个点，邻域法就是找出离距离半径为的园内的所有样本点。

（2）构造邻域图。

若与为近邻点，则边的权值为与之间的欧氏距离，记为。

否则。

（3）计算距离矩阵。

若与为近邻点，即为近邻点，

则，否则。

然后对逐个样本点顺次计算。

（7）

（4）应用MDS算法求得低维嵌入坐标。

根据等距离算法得到的欧式距离如图2所示。

根据欧式距离图得到对应的测地线距离根据以上的算法步骤得到降维后的数据如图3所示。

4.2 局部线性嵌入

该方法是最早提出的一种非线性降维的方法，该方法的特点主要处理非线性类数据，通过将非线性的数据转换成局部线性的数据，同时保持数据间距离对应关系等，使其拓扑关系不发生变化，因此该方法的特点是处理非线性的数据同时具备线性数据的处理速度，因此此方法广泛地应用于维数约简算法中，具体算法步骤如图4所示。

（1）确定局部邻域：假设流形数据集为，单个数据样本点表示为，，其中为样本点个数，为样本点维数，为近邻点个数。样本点与之间的距离为

（8）

（2）计算局部重构权值矩阵，定义误差函数，使其把用其近邻的线性组合表示的误差最小

（9）

其中，为的个最近邻点为与之间的权值。

对于样本点的近邻点权值矩阵通过以下方法计算求得：

计算邻接关系矩阵

即矩阵的元素是对应的两个邻接点的内积，并求出矩阵的逆矩阵。

计算拉格朗日因子，是保证对的归一化操作：

令 （10）

其中，，。

求

（11）

（3）利用权值矩阵求低维嵌入坐标，其中保持不变。

（12）

并且满足

其中，表示维单位阵，就是降维后的数据。

上述优化问题可以转化为下列带约束优化问题

（13）

其中，，要使损失函数值达到最小。使用Lagrange乘子法则取为的个非零特征值所对应的特征向量。在處理过程中将特征值由小到大排列，通常第一个特征值几乎为零，取2到个特征值所对应的特征向量作为输出结果。

4.3 拉普拉斯特征映射算法

该算法与上述算法[9，10]也有很多相似之处，该方法是将数据间的关系用图的形式表示出来，通过构造数据间的邻接表来表示数据，数据表示图的一个顶点，同时邻近表中重复的数据我们用图的相似度来表示，通过这样的一张无向有权图来处理流形数据就是该算法的核心思想。具体的算法步骤如下：

（1）构造无权有向邻接图。使用近邻或近邻，对每个样本点的个近邻点分别连上边。或是一个预先赋定的值。

（2）确定权重：确定样本点之间邻接关系权重的大小，求权重时有两种方法可供选择。

a.简单化设定，若点与为近邻点，则令，否则。

b.选用热核函数来确定，若点与为近邻点，那么它们关系权重否则为0。

（3）计算低维嵌入向量，Laplacian Eigenmaps要优化的目标函数如下：

（14）endprint

定义对角矩阵，对角线上位置元素为矩阵第行元素之和，上述优化问题等价于以下优化问题：

（15）

次优化问题最终转化为解下列广义的特征向量问题。

（16）

其中，为对角矩阵，，为近邻图的拉普拉斯算子，，使用最小的m个非零特征值对应的特征向量作为降维后的结果输出。

4.4 局部切空间排列算法

该方法是由浙江大学张振跃等提出的[11，12]，该方法的特点就是构造出数据样本的局部切空间，而将这样的切空间数据用对应的邻域表来表示，进而将这些切空间数据嵌入到这样的邻域表，进而完成了高维的D维空间嵌入到d维空间中，具体的描述步骤如下所述。

非线性降维的目的是：在嵌入映射函数具体表达式未知下从函数值得到其低维的坐标表示。

假设嵌入映射足够光滑，在确定的点处应用泰勒定理，得到下列泰勒式：

（17）

其中，为映射在处的雅克比矩阵，为的一个近邻点，则有

（18）

由的个列向量张成在处的且空间，即，向量便为对应放射子空间的一阶逼近局部坐标，因具体表达式未知，无法计算出雅克比矩阵，故可借助的表达式来表示，由的一组标准正交基组成的矩阵，即有形式

（19）

其中，的值依赖于局部结构中心的值。

令，则

（20）

式（20）中表示放射变换矩阵。

全局坐标表满足

（21）

其中，为的邻域，为了逼近全局坐标，需要寻求全局坐标系和局部放射变换是上述表达式误差最小。故我们的目标可总结为寻求全局坐标系统和局部坐标变换使下式达到最小

（22）

LTSA算法步骤如下[13]：

（1）构造局部邻域。取离最近的个样本点作为的近邻点，构成的邻域矩阵，其中。

（2）局部线性投影。对每个样本点的邻域，求其中心化矩阵

（23）

其中，即为元素全为1的列向量，对中心化后的矩阵进行奇异值分解

（24）

其中，，为的非零奇异值。

和的列向量分别为一组标准正交基，。

取的前列构成矩阵。依据下式计算出局部坐标

（25）

（3）局部坐标系统排列。

全局坐标系统是所有交叠的局部坐标系统排列得到。同时整体坐标应满足

（26）

其中，，是待求得局部放射变换，为局部重构误差，若令，，则

（27）

式（27）为重构误差的表达式。

为在保持局部拓扑结构求得低维嵌入坐标，本算法通过使全局坐标排列的重构误差达到最小来得到全局坐标：

（28）

5 算法比较分析（Algorithm comparison analysis）

上文讲述了不同的维数约简算法的原理和数学构造方法，接下来我们就从运行时间、复杂度分析和参数设置和算法特点几个方面给予分析比较，具体结果如表1、表2、表3所示[14-16]。

6 结论（Conclusion）

文章介绍了维数约简的数学定义，从本质上对维数约简进行了分析介紹，维数约简的本质是降维，对于数据的降维分为线性降维和非线性降维，因此维数约简算法也分为线性和非线性，本文主要介绍了线性典型算法有主成分分析PCA算法和多维尺度变换算法[20]，非线性算法着重介绍了等距特征映射，局部线性嵌入，拉普拉斯特征映射，局部切空间排列算法，并对各个算法的优缺点进行了分析，文章从宏观上对每个算法进行了简要的描述，仅对有兴趣致力于该方面研究的科技工作者给予参考和借鉴。

参考文献（References）

[1] 陈省身，陈维恒.微分几何讲义[M].北京：北京大学出版社，

1983.

[2] Silva V De，Tenenbaum J B.Global versus local methods in nonlinear dimensionality reduction[J].Neural Information Processing Systems，2002，15：705-712.

[3] Pearson K.On lines and planes of closest fit to systems of points in space[J].Philosophical Magazine，1901，2（6）：559-572.

[4] 谭璐.高维数据的降维理论及应用[D].长沙：国防科学技术大学研究生院，2005.

[5] 尹俊松.流形学习理论与方法研究及在人脸识别中的应用[D].长沙：国防科技大学硕士学位论文，2007.

[6] 马驰，张红云，苗夺谦.改进的主曲线算法在指纹骨架提取中的应用[J].计算机工程与应用，2010，46（16）：170-173.

[7] 吴晓婷.基于流形学习的数据降维算法研究[D].大连：辽宁师范大学硕士论文，2010.

[8] Tenenbaum J B.Silva V de.Langford J C.A global geometric framework for nonlinear-ensionality reduction[J].Science，

2000，290（5500）：2319-2323.

[9] Belkin M，Niyogi P.Laplacian eigenmaps and spectral techniques for embedding and clustering[J].Neural Information Processing Systems，2002，14：585-591.endprint

[10] 屠红磊，黄静.基于K段主曲线算法的手绘形状识别[J].计算机应用，2009，29（2）：456-458.

[11] Zhang Zhen-yue，Zha Hong-yuan.Principal manifolds and nonlinear dimensionality reduction via local tangent space alignment[J].SIAM Journal of Scientific Computing，2004，26（1）：313-338.

[12] Zhang Zhen-yue，Zha Hong-yuan.Linear low-rank approximations and nonlinear dimensionality reduction[J].Science in China Series A-Mathematics，2005，35（3）：

273-285.

[13] 雷晓花.流形学习研究及在文字识别中的应用[D].天津：中国民航大学硕士论文，2011.

[14] 肖睿.高维空间模式鉴别分析及多流形学习[D].上海：上海交通大学电子信息与电气工程学院自动化系，2011.

[15] 侯文广，等.基于流形学习的三维空间空间网格剖分方法[J].電子学报，2012，37（11）：2579-2583.

[16] 黄启宏，刘钊.流形学习中非线性维数约简概述[J].计算机应用研究，2007，24（11）：19-25.

[17] 张学工.模式识别[M].北京：清华大学出版社，2002.

[18] 胡洁.高维数据特征降维研究综述[J].计算机应用研究，2008，

25（9）：2601-2602.

[19] 王庆刚.流形学习算法及若干应用研究[D].重庆：重庆大学博士学士论文，2009.

[20] 李光，等.基于流形理论的数据分类挖掘[J].舰船电子工程，2009，29（5）：91-93.

作者简介：

马发民（1986-），男，硕士，助教.研究领域：仿生算法，智能优化算法.

张 林（1968-），男，硕士，教授.研究领域：网络安全.

王锦彪（1947-），男，硕士，教授.研究领域：蚂蚁算法，仿生算法.endprint