混响室条件下失真信号消噪技术研究
2017-09-28王川川张晓芬赵琳锋
贾 锐,王川川,张晓芬,赵琳锋
(电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003)
混响室条件下失真信号消噪技术研究
贾 锐,王川川,张晓芬,赵琳锋
(电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003)
为研究混响室条件下失真信号消噪恢复技术,采用Mallat算法和预失真技术的失真数据补偿方法,首先,利用蒙特卡洛方法(Monte Carlo)模拟混响室内电磁环境,获得全向辐照电磁环境和接收系统的联合传递函数;再将联合传递函数的反函数置于预失真器中,用于补偿信号通过混响室内全向辐照电磁环境和接收系统后产生的误差和畸变。利用验证信号进行验证,结果表明该方法可有效消除系统带来的误差,较好地恢复和保持了接收信号信息。
混响室;Mallat算法;预失真技术;数据补偿;失真
0 引言
混响室技术(RC)被广泛应用于各种电磁兼容性测试[1],包括辐射敏感度[2]、辐射发射[3]、屏蔽效能[4]、天线效率[5]、探针校准以及材料特性等测试[6]。国内主要利用混响室进行辐射敏感度和屏蔽效能测试,前者主要是通过视觉观察来判断受试设备是否达到敏感极限再记录下当时的干扰强度。而视觉观察受到试验人员主观判断影响较大,不同的试验人员对受试设备所处状态的判断可能会有很大的不同,因而影响了试验结果的准确性、可重复性。所以需要一个客观的判断标准来衡量受试设备的工作状态,一种方法是将受试设备的输出信号作为判断依据,根据输出信号的波形信息来判断受试设备的状态。但信号从受试设备至数据处理终端过程中必将受到各种因素的影响,如混响室内全向辐照电磁环境、传输线缆的非线性特性、天线系数、探头转移阻抗以及接收系统等,这些因素都会对受试设备输出信号造成很大影响,从而产生偏差和畸变。若是不对这些畸变和失真进行处理,接收机终端收到的信号与原始信号将会有非常大的偏差,而基于这些信号的后续工作都会受到严重影响。因此,研究混响室条件下传输信号消噪技术具有非常大的现实意义。
一方面,传输线缆在混响室环境中,会产生与理想单一方向入射的平面波辐照完全不同的响应效果,国内外很多学者都对此进行了非常深入的研究。但研究重点都是传输线上的感应电流及其分布规律,而没有涉及如何将有用信号与干扰信号分离,获得与受试设备输出信号一致的接收信号;另一方面,在实际的测试过程中,由于试验人员的主观性造成试验结果的不确定性迫切需要解决。正是基于此,提出了混响室条件下的信号消噪方法,方法分为两部分:① 干扰系统信息收集部分,也可称为校准过程,利用蒙特卡洛方法(Monte Carlo)模拟混响室内电磁环境,从中提取已知信号,获得全向辐照电磁环境和接收系统的联合传递函数;② 失真信号消噪重构部分,将联合传递函数的反函数置于预失真器中,可补偿2个干扰系统带来的失真。
1 混响室内电磁环境
典型机械搅拌混响室的结构为高导电率的屏蔽腔体内装配1个或多个由高导电率金属建造的机械搅拌器[7]。通过搅拌器的转动,改变腔室内电磁环境的边界条件,改变腔室内电磁场模结构[8],使其工作于过模状态[9-10],从而在腔室内部激发出统计意义上的场强均匀、各向同性、随机极化的电磁场[11-14]。由此原理,近年来源搅拌、频率搅拌、不规则混响室相继出现,在电磁兼容测试领域都发挥了重要的作用。混响室腔室测试区域电场分布规律如图1所示。
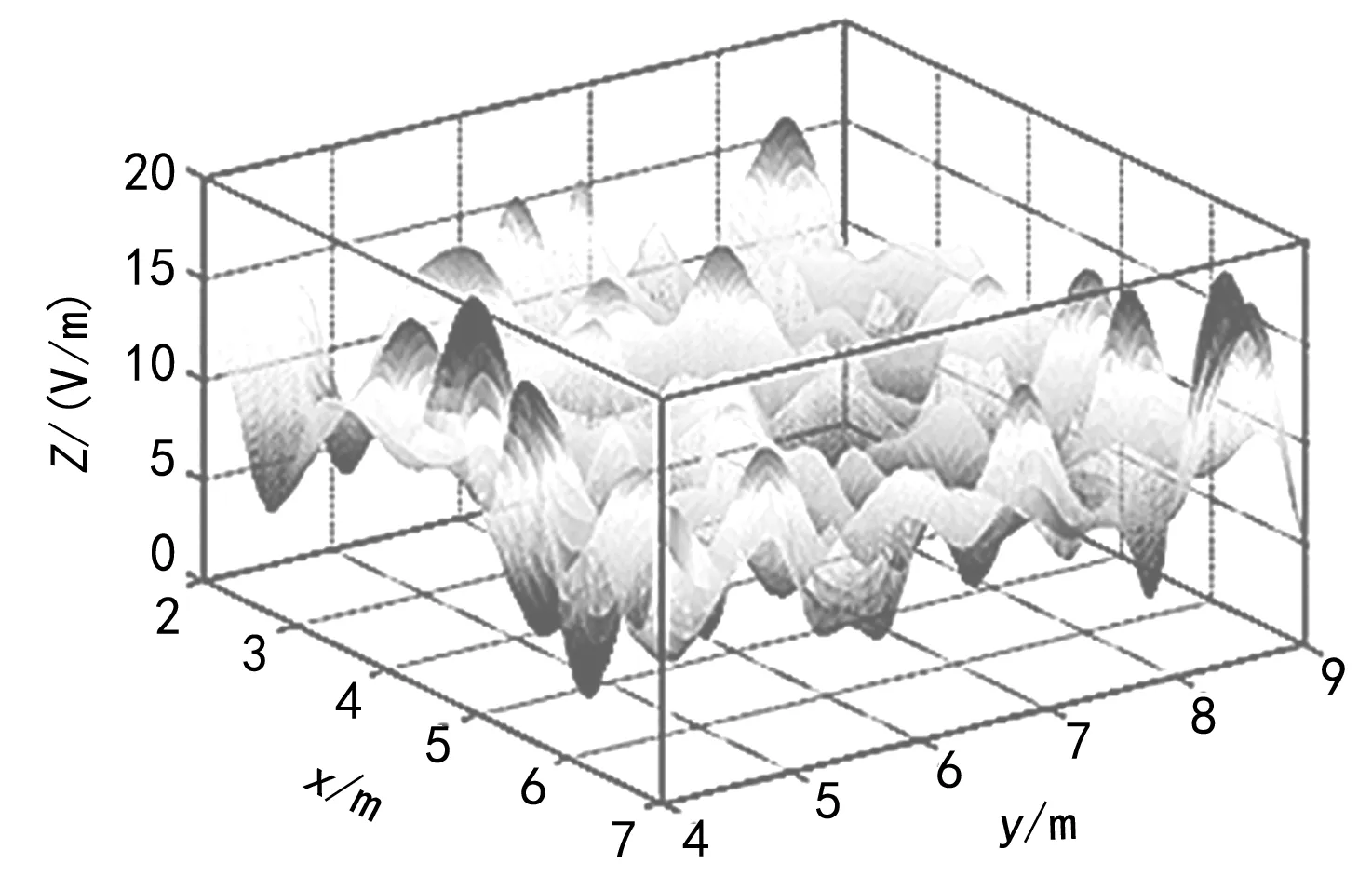
图1 混响室电场分布
混响室工作区内3个正交电场的电磁分量,其电磁场分布呈现为随机起伏、不均匀状态。图1中给出的是一个边界条件下的场分布,经多个搅拌位置叠加后,即多个图1中电磁场分布进行叠加后,混响室内电磁场就会呈现出统计均匀的特性,如表1所示。真实空间中,由于空中云层、地面起伏、各类建筑物构筑物的散射,战场上武器装备或空间中电子设备都不会只受到一个方向上的电磁干扰,更多情况下是多个方向(或全向)同时受到影响,尤其是在局部战场或电子设备布局较密位置特别是在腔室电磁环境内。而与传统理想电磁试验环境不同,位于混响室测试区域内的受试设备会同时受到360°随机的电磁辐射。因此,混响室内电磁环境更加接近真实空间电磁环境,这便是混响室与其他理想条件下电磁环境的最大区别。
表1 混响室内电磁场量分布模型

混响室内电磁场量分布规律分布模型ReEx,y,z(),ImEx,y,z()正态分布fR()=12πσ2exp-R-μ()22σ2()R=ReR'()Im(R'),R'=Ex,y,z,IinducedEx,y,z瑞利分布fR()=Rσ2exp-R22σ2()R=Ex,y,z,IinducedEx,y,z2指数分布fR()=12σ2exp-R22σ2()R=Ex,y,z,Iinduced
正是由于混响室内电磁环境与理想电磁环境明显不同,在处理其条件下的信号传输问题时,除了传输线缆特性之外,还要考虑到这类服从特定分布规律的全向辐照电磁环境对信号的影响。利用基于统计理论的蒙特卡洛方法模拟混响室内全向辐照的电磁环境,而蒙特卡洛方法模拟混响室电磁环境的有效性已经在多篇文献中得到证明。
2 消噪原理方法
小波分析在信号处理方面有着非常广泛的应用,小波变换被称为数学显微镜,其突出特点是有多分辨率,能克服短时傅里叶变换的不足,对信号具有自适应性,窗口大小可随频率变化,因此可用于分析非平稳信号时域和频域的微观信息[15]。而Mallat算法主要基于多分辨率分析的多采样率滤波器组分解信号,可把信号分解为离散平滑分量和离散细节分量。从空间的概念上对小波的多分辨分析特性进行了论证,建立了多分辨分析的概念[16]。
应用二尺度方程
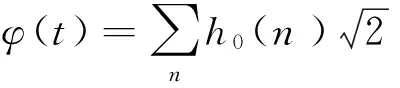
根据多分辨率分析,将信号分解为离散平滑分量和离散细节分量,可以得到递推的Mallat分解算法为[17-18]:
(1)
(2)
式中,cj,k为离散平滑分量;dj,k为离散细节分量,又分别为第j层的尺度系数和小波系数;h0和h1分别为低通和高通滤波系数,分别输出信号的低频信息和高频信息。上式表明其可由第j-1层的尺度系数经过滤波器进行加权求和得到。
因此信号可重构为:
(3)
信号的分解与重构过程中,h*0和h*1分别为低通和高通滤波系数的反变换,如图2所示,为正交滤波器组,其输出信号带宽均为原信号带宽的一半,采样速率也随之减半。向下的箭头和向上的箭头分别表示二抽取和二插值,分别对应在每隔对应样本数量抽样或插值一次,数据长度也随之减半和增加一倍,从而恢复至原始信号长度。由图2可知,信号的分解和重构互为逆过程。信号重构过程中,插值后的数据需经过低通和高通滤波器处理,目的是为了将补零后的波形做平滑处理。
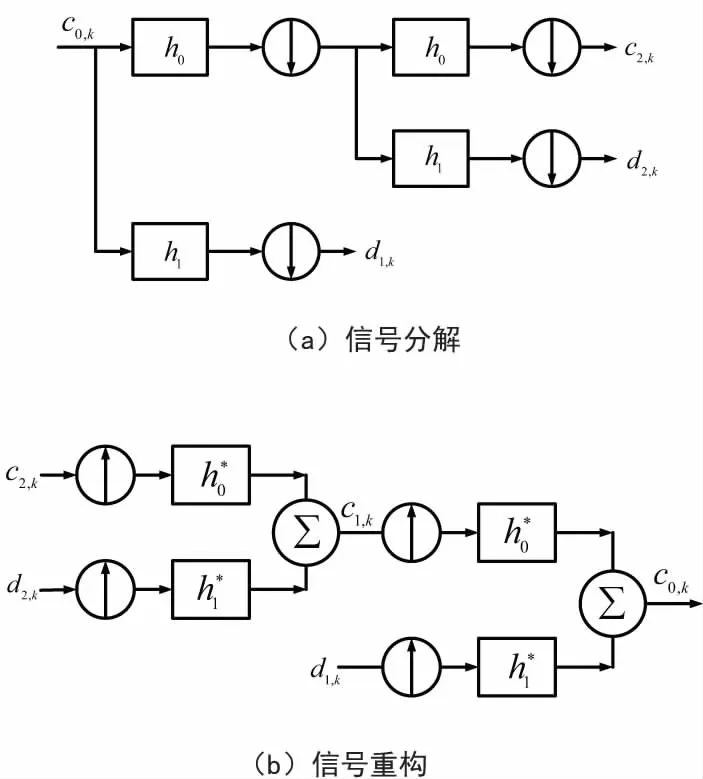
图2 信号的分解与重构
预失真技术一般应用于功率放大器的信号失真处理[19-20],在功率放大器前对输入信号先做预处理,它的传输特性为放大器特性的反函数。当输入信号经过预失真和放大器模块之后,输出信号就只剩下线性增益[21-23],这样就实现了对功放模块引入噪声的消除。

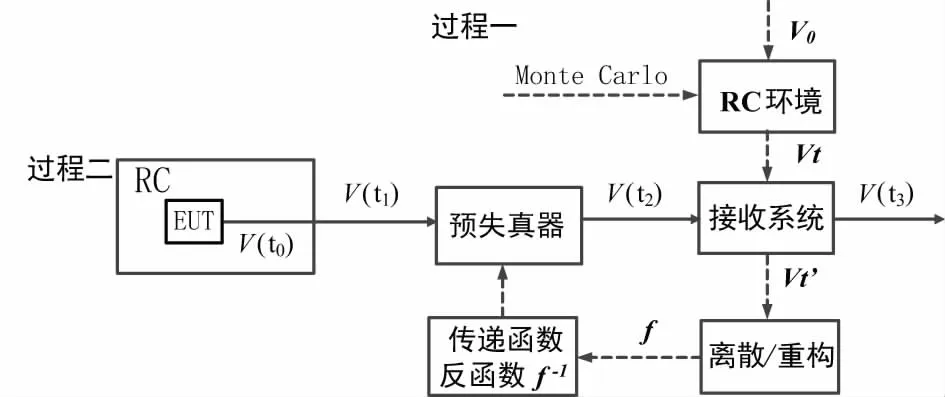
图3 方法原理
3 实例验证
为使算法过程更加形象化,将受试设备的输出信号定义为y=10cos(2π·90t)e-30t,考察其依次通过混响室全向辐照电磁环境和接收系统后的信号畸变情况。由于其非线性特性,原信号在经过2个干扰系统后,会在特定区间内叠加上噪声,这里设定叠加时间区间为60~70 s,这个区间内的信号将会产生一定程度的失真。本文的目的就是尽量消除该区间内的失真,使受到混响室全向辐照电磁环境和接收系统干扰的输出信号最大程度的接近原始信号。由图4 所示,验证信号受到干扰后,在叠加区间内产生了较大失真,叠加区间内2个信号的相关系数下降至0.56,说明信号畸变已经达到一定程度,会对后续的信号分析造成非常大的影响,甚至造成误判断。通过2个过程的处理后,恢复信号与验证信号在叠加区间内的相关系数为0.99,说明该方法能够满足失真信号补偿恢复的要求。

图4 原信号和重构信号对比
4 结束语
本文提出了一种混响室条件下基于小波算法和预失真技术的失真信号恢复方法。在介绍了混响室内电磁环境分布规律和工作原理的基础上,对所提出方法的流程进行了介绍。选定某种信号进行算法验证,该方法首先利用Mallat算法对受到全向辐照和接收系统2个干扰系统影响的接收信号进行分解和重构,得到系统联合传递函数,然后将其反函数置于预失真器中,经过处理得到的波形与原波形有较好的一致性。本文方法只需要对接收信号进行处理即可得到系统引入的畸变,不需要额外系统信息,最大化地简化了实现过程,提高了后续分析的稳健性和可靠性,为扩展混响室应用和信号消噪技术提供了基础。
[1] IEC61000-4-21,Electromagnetic Compability(EMC)-Part 4-21:Testing and Measurement Techniques-Reverberation Chamber Test Methods[S],2011.
[2] 刘逸飞,陈永光,王庆国,等.频率搅拌混响室场均匀性与搅拌带宽选取方法分析[J].高电压技术,2012,38(9):2354-2359.
[3] 贾锐,王庆国,程二威.混响室散射场条件下的场线耦合数值计算[J].高电压技术,2012,38(11):2823-2827.
[4] 袁智勇,何金良,曾嵘,等.电磁兼容试验中的混响室技术[J].高电压技术,2005,31(3):56-58.
[5] MADSENK,HALLBJORNER P,ORLENIUS C.Models for the Number of Independent Samples in Reverberation Chamber Measurements with Mechanical,Frequency,and Combined Stirring[J].IEEE Antennas and Wireless Propagation Letters,2004,3(1):48-51.
[6] 王庆国,贾锐,程二威.混响室连续搅拌工作模式下的辐射抗扰度测试研究[J] .高电压技术,2010,36(12):2954-2959.
[7] ANDRIES M I,BESNIER P,LEMOINE C.Estimating K-Factor and Time Spread Parameters from a Transient Response of a Pulse Modulated Sine Wave in Reverberation Chamber[J].Antennas and Propagation,IEEE Transactions on,2013,61(1):380-389.
[8] ARTZ T,HIRSCH H.PulsedSignals in Reverberation Chambers:Experimental Analysis of Transient Peaks[C]∥Proceedings of the Electromagnetic Compatibility(EMC EUROPE),International Symposium on Electromagnetic Compatibility,2013:365-368.
[9] HILL D A.Electromagnetic Fields in Cavities[M].Electromagnetics Division National Institute of Standards and Technology,2009.
[10] MADSENK,HALLBJORNER Pl,ORLENIUS C.Models for the Number of Independent Samples in Reverberation Chamber Measurements with Mechanical,Frequency,and Combined Stirring[J].IEEE Antennas and Wireless Propagation Letters,2004,3(1):48-51.
[11] LANGLEYR S.A Reciprocity Approach for Computing the Response of Wiring Systems to Diffuse Electromagnetic Fields[J]. IEEE Trans.on Electromag.Compat.,2010,52(4):1041-1055.
[12] ISABELLE J,JEAN P,PIERRER D.Field-to-wire Coupling in an Electrically Large Cavity:a Semianalytic Solution[J].IEEE Trans.on Electromag.Compat.,2010,52(4):1034-1040.
[13] HUABIN Z,XIANG Z,QINGCHUN L,et al.An Alternative Semianalytical/Analytical Solution to Field-to-Wire Coupling in an ElectricallyLarge Cavity[J].IEEE Trans.on Electromag.Compat.,vol.2012,54(5):1153-1160.
[14] BRADLEY D T,M LLER-TRAPET M,ADELGREN J,et al.Effect ofBoundary Diffusers in a Reverberation Chamber:Standardized Diffuse Field Quantifiers[J].The Journal of the Acoustical Society of America,2014,135(4):1898-1906.
[15] 裴善报,刘荣忠,郭锐.基于小波变换的水下连续爆炸声信号特征分析[J].爆炸与冲击,2015,35(4):520-526.
[16] 杨福生.小波变换的工程分析与应用[M].北京:科学出版社,1999.
[17] 彭玉华.小波变换与工程应用[M].北京:科学出版社,1999.
[18] 王绍华,周睿,宋立军.编程实现Mallat小波算法研究[J].海军大连舰艇学院学报,2004,27(2):60-62.
[19] 张书亮.OFDM系统中数字预失真技术研究[D].西安:西安电子科技大学,2011.
[20] 蔡敏.基于自适应IIR滤波器的数字预失真算法研究[D].西安:西安电子科技大学,2011.
[21] 任智源,张海林.一种宽带OFDM系统放大器的失真消除方法[J].中国科学,2011,41(6):726-738.
[22] XU Ling-jun,WANG Qiang,WU Xiao-guang,et al.Adaptive Digital Predistorter for Radio Frequency Power Amplifier Linearization[C]∥IEEE International Symposium on Microwave,Antenna,Propagation,and EMC Technologies for Wireless Communications,2007:1390-1393.
[23] ROBINP.Frequency-Selective Predistortion Linearization of RF Power Amplifiers[J].IEEE Trans.Microwave Theory and Techniques,2008,56(1):65-75.
ResearchonNoiseEliminationTechnologyinReverberationChamber
JIA Rui,WANG Chuan-chuan,ZHANG Xiao-fen,ZHAO Lin-feng
(StateKeyLaboratoryofComplexElectromagneticEnvironmentEffectsonElectronicsandInformationSystem,LuoyangHe’nan471003,China)
In order to eliminate the distortions from the electromagnetic field inreverberation chamber and receiving system,one method based on Mallat algorithm and predistortion technology is proposed in this paper.Firstly,the reverberation chamber can be simulated by Monte Carlo method,and the united transfer function of omnidirectional radiation electromagnetic environment and receiving system can be obtained.Furthermore,the inverse function of united transfer function is embedded in the predistortion component to compensate the signal error and signal distortion caused by omnidirectional radiation electromagnetic environment and receiving system.One waveform is chosen to verify this technology,and the results show that the proposed method can effectively eliminate the errors from system,and can significantly recover and maintain the
signal information.
reverberation chamber;Mallat algorithm;predistortion technology;data compensation;distortion
10.3969/j.issn.1003-3106.2017.10.13
贾锐,王川川,张晓芬,等.混响室条件下失真信号消噪技术研究[J].无线电工程,2017,47(10):59-62.[JIA Rui,WANG Chuanchuan,ZHANG Xiaofen,et al.Research on Noise Elimination Technology in Reverberation Chamber[J].Radio Engineering,2017,47(10):59-62.]
TN97;O441
A
1003-3106(2017)10-0059-04
2017-07-06
国家自然科学基金资助项目(51277180)。
贾锐男,(1986—),博士,助理研究员。主要研究方向:电磁环境模拟及信号处理。王川川男,(1985—),博士,助理研究员。主要研究方向:电磁环境效应评估及盲源信号处理。
