基于向量组法的小电流接地故障暂态网络建立
2017-09-28孙润诚赵宏伟孟庆武田志刚刘国松
孙润诚,赵宏伟,孟庆武,田志刚,刘国松
(后勤工程学院 机械电气工程系, 重庆 401311)
【信息科学与控制工程】
基于向量组法的小电流接地故障暂态网络建立
孙润诚,赵宏伟,孟庆武,田志刚,刘国松
(后勤工程学院 机械电气工程系, 重庆 401311)
以小电流系统单相接地故障为研究对象,针对传统向量法难以应用于暂态过程的问题,提出了以含多频多幅值分量的向量组表示暂态电气量网络,简化暂态过程的计算方法,利用以向量组表示的节点电压方程,消去部分支路节点,添加母线及负载中性点的对地电流,加入部分受控源补偿缺失电压得到新的暂态等值网络;建立的暂态简化网络严格满足暂态方程的约束,具有较高的精度和适用性。
小电流接地系统;向量组;节点电压方程;方程约束
在我国中压配电网中,电力系统的中性点一般采用消弧线圈接地或不接地方式。当线路发生单相接地短路时,由于不能形成低电阻的短路回路,故障点的电流较小,故称小电流接地电网[1]。小电流接地系统发生单相接地故障时,其具有故障电流较小,线电压保持对称性,可带故障运行等特点。但长时间的带故障运行,易产生多点接地短路、全系统过电压、绝缘损害等不利情况,进而危害系统的正常运行。所以由小电流接地故障衍生的各类技术,包含故障的选线和定位、中性点补偿、过电压防护等,具有很强的现实意义,也是近年该研究领域的热点和难点。
小电流接地系统的故障过程可分为稳态过程和暂态过程,早期的研究[2-5]主要对稳态过程进行分析,建立了较为完善的稳态故障理论,但受制于稳态信号的幅值较小、故障特征不明显,稳态故障理论的实际效果并不理想。由于暂态过程具有幅值大、频谱广的特点,可以为故障分析提供丰富的信息,近年来越来越多的研究开始集中于小电流接地故障的暂态分析[6-8]。
近年来,研究暂态分析的主要内容是通过数字仿真技术得出暂态特征,并采用新型数学工具(如傅里叶变换、小波变换、粗集等)处理故障信号。而在暂态过程产生原理、暂态等值网络等方面,现阶段的研究明显不足。
传统暂态等值电路[9]为零模网络集中参数等效电阻、电感与对地分布电容构成的 RLC 串联电路。该模型仅与零模回路有关,忽略接地电阻的影响,且缺乏参数计算方法,误差无法估算,难以准确定量描述暂态过程。因此,建立小电流接地故障暂态过程的高精度等值电路,对认识暂态现象的本质,更准确地把握、分析暂态量变化规律十分重要。
本文提出一种了以维持暂态方程约束不变为中心的暂态网络建立方法。针对传统向量法难以表示暂态电气量的问题,以含多频多幅值分量的向量组表示暂态电气量,通过暂态节点电压方程组的约束简化网络,得出含受控源的等值网络,大大减少了暂态网络节点数。最后利用数字仿真从不同暂态等值网络与实际网络的暂态信号对比,验证了该模型具有较高的准确度。
1 用向量组表示暂态分量
电路暂态过程中出现的各种暂态分量具有Fe-βtsin(ωt+φ)的形式[10]。当ω=0时,为按指数规律衰减的非周期暂态分量(直流分量);当ω≠0时,则为振荡衰减的周期性暂态分量。
实际上对于暂态分量,也可以用类似于正弦稳态分量一样采用旋转向量在虚轴(或者实轴)上的投影来表示。不同之处在于,对于正弦稳定信号来说,向量是匀速转动且模不变;对暂态信号来说,是由多个向量相加而得,这些向量的模随时间变化,且向量之间的转速不同,甚至存在静止不动的向量(非周期性暂态分量)。
因此,对于暂态过程中的电流、电压I和U,可以用相应的复数表示,以电流为例:

用此向量组表达的暂态电压、电流的关系如下:设两端电压为
1) 对于电阻元件来说,通过的电流为
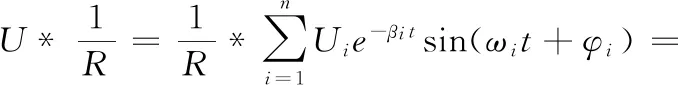
即
2) 对于电容元件来说,通过的电流为
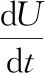
即
3) 对于电感元件来说,同电容得
2 节点电压方程约束下的暂态等值网络
2.1 传统故障暂态等值电路
根据文献[11],传统小电流接地系统单相接地故障的暂态等值电路如图1所示。图1中:C0Σ为所有出线对地分布电容之和;L0T为考虑电源变压器与线路的零模等效电感;R0T为零模等效电阻以及3倍的故障点过渡电阻之和;Lp为3倍消弧线圈电感;Uf(t)为故障点虚拟电源,等于故障点故障前的反相电压;开关S打开为不接地方式,闭合为经消弧线圈接地方式。

图1 传统单相接地故障暂态等值电路
传统暂态等值电路存在以下问题:
1) 仅包含零模信息,忽略了线模分量在暂态过程中的作用[12-13]。
2) 此模型仅能得出故障点的电压及对地电流,这些电气量在实际配网故障中难以测量,因此不能对故障的选线和定位、过电压防护等提供可靠信息。
3) 消弧线圈连接于故障点处,与实际不符,无法验证模型的准确度。
2.2 无损暂态网络的建立
由于小电流接地系统多用于配电网末端、单相接地故障原因多样,其暂态网络具有馈线长度短、单线负载相对较低、对地电容不可忽略、接地电阻和接地位置不定等特点[3]。根据以上特点,在考虑到以下几个条件的情况下,建立了如图2所示的无损暂态网络,此网络具有很高的精度。

图2 无损暂态网络模型
1) 配电网一般馈线长度较短,输电线路可采用π模型保证精度;
2) 变压器二次侧至母线段可用一个π模型代替线路阻抗和变压器内阻;
3) 馈线末端设置为感性三相对称负载,连接方式为Y型;
4) 存在不为0的接地电阻;
5) 由于配电系统负荷相比于整个电力系统较小,且其中性点采用小电流接地方式,不会对系统的正常运行产生过大影响,故对于故障的暂态过程可仅考虑电磁暂态,不考虑机电暂态过程,即变压器二次侧输出电压稳定,可用恒定电压源代替。
该网络中共有4n+9节点,而在实际配网中,母线处的各相电压及各馈线电流是可实时监测,也是故障保护、检测、选线的主要数据来源。相反地,对于馈线1~n近负载节点L1a~Lna、L1b~Lnb、L1c~Lnc,近变压器节点Ta、Tb、Tc,以及故障处节点F,其节点电压和对地电流在实际中难以检测,难以为故障保护、检测、选线的提供有效数据。故在下步的暂态网络简化中,主要考虑母线节点Ba、Bb、Bc,处的电压信号,尽量消去其他节点。
2.3 无损暂态网络的化简
由本文第1节,在暂态电路中,当电流和电压采用向量组表示后,其满足如下关系:
1) 电阻元件
2) 电容元件
3) 电感元件
固对于节点A、B形成的支路,支路电流可表示为

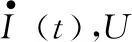
Ta(Tb,Tc略):
IA=UTaYTa-G+(UTa-UBa)YTa-Ba
(1)
Bc(Ba,Bb略):
(UTc-UBc)YTc-Bc=UBcYBc-G+(UBc-UF)YBc-F+
(2)
(3)
Ei:(ULia-UEi)YLia-Ei+(ULib-UEi)YLib-Ei+
(ULic-UEi)YLic-Ei=0
(4)
F:(UBc-UF)YBc-F=UFYF-G+
(UF-ULnc)YF-Lnc=0
(5)
UTa(UTb,UTc略)=UA+UN
(6)
实际故障中L1a~Lna、L1b~Lnb、L1c~Lnc、Ta、Tb、Tc及F节点的电压测量难度大,不具备参考价值;而Ba、Bb、Bc、N节点的电压测量方便,便于为暂态过程提供信息。故可将上述方程联立,消去L1a~Lna、L1b~Lnb、L1c~Lnc、Ta、Tb、Tc处节点电压,以A相为例,联立后的方程如下:
Ba:IA=(UBa-U2)YTa-G+UBaY1+
(7)
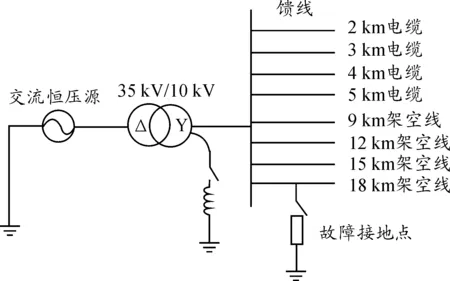
Ei(i (UBc-UEi)Y4-UEiY5=0 (8) (9) 其中 Y6=-YTa-Ba 暂态模型的评价可转化为模型在相同激励下暂态响应的误差评价。以无损暂态电路为参照,通过对比传统暂态等值电路和化简后的暂态等值电路在故障点的对地电流,以及母线处的暂态零序电压,对本文所建立的简化暂态等值电路进行评价。 图3 简化暂态网络模型 由于传统暂态等值电路仅能以故障点对地的暂态电流作为误差分析的根据,本文用于仿真的简化暂态模型对于故障馈线并没有化简,保留了故障节点,方便仿真对比。 利用ATP电磁暂态仿真软件,建立一个具有8条出线的35/10 kV中性点经消弧线圈接地系统(图4),采用过补偿,过补偿度为8%,含2 km、3 km、4 km、5 km长电缆出线四路,9 km、12 km、15 km、18 km架空出线四路,共8回路。以故障点位于 18 km长线路上距母线9 km处为故障点,接地电阻分别为1 Ω,5 Ω,10 Ω,各模型(传统暂态模型、无损暂态模型、简化暂态模型)的故障点暂态对地电流波形如图5所示。 对于无损模型和简化模型,都可以得到母线处的各相暂态电压波形,这是实际变电站中的重要数据,同样设置接地电阻分别为1 Ω,5 Ω,10 Ω,二者的母线暂态零序电压波形如图6所示。 图4 仿真模型拓扑 图5 各模型故障点对地暂态电流 从图5和图6可以看出: 1) 本文所建的暂态简化电路在对故障点接地电流的模拟上,明显优于传统暂态等值电路,与无损暂态模型基本吻合; 2) 本文的暂态简化电路模拟精度受接地电阻的影响,当接地电阻达到5 Ω时,已经具有较高的精度,能满足实际接地故障中存在一定接地电阻的条件; 3) 当故障波形趋于稳态后,本文的暂态简化电路误差逐渐增大,这是由于稳态时电气量不能用向量组表示,基于向量组简化的电路会逐渐失真。 针对不同故障条件(如故障点位于不同线路不同位置、不同过渡电阻等)、不同系统结构 (中性点不同接地系统、有无电缆出线等),进行了大量的仿真验证,其结果与上述情况类似,不一一叙述。 1) 利用向量组表示暂态电气量,得出了在暂态过程中,流经不同器件电流和其两端电压的数学关系; 2) 根据小电流接地系统的实际情况,提出了电网建模的若干条件,建立了无损暂态电网模型;利用节点电压法列出方程并消去不必要节点,得到母线处各节点的约束方程,根据约束方程建立了新的简化网络; 3) 经过仿真可以发现,提出的简化网络在暂态分析时具有很高的精度,但由于向量组不能表示稳态电气量,不适用于故障的稳态分析。 [1] 中国电机工程学会自动化专委会配电自动化分专委会秘书组.配电自动化专委会学术讨论中关注的问题[J].电网技术,1999,23(1): 68-69. [2] 贺家李,宋从矩.电力系统继电保护原理[M].北京:中国电力出版社,2001. [3] 程路,陈乔夫.小电流接地系统单相接地选线技术综述[J].电网技术,2009,33(18):219-224. [4] 曾祥君,尹项根,张哲,等.配电网接地故障负序电流分布及接地保护原理研究[J].中国电机工程学报,2001,21(6):84-89. [5] LIN Xiangning,ZHAO Zhimin,BO Zhiqian.An adaptive inverse time-delay characteristic of the zero-sequence overvoltage protection for identification of the single-phase earth fault in the neutral non-effectively grounded power systems[C]//Power & Energy Society General Meeting,2009.PES’09.IEEE. [6] ABDEL-FATTAH M F,LEHTONEN M.Transient algorithm based on earth capacitance estimation for earth-fault detection in medium-voltage networks[C]//Generation,Transmission & Distribution,IET,2012,02. [7] 赖平,周想凌,邱丹.小电流接地系统暂态电流频率特性分析及故障选线方法研究[J].电力系统保护与控制,2015(4):51-57. [8] 张淑清,马跃,李盼,等.基于改进的广义谐波小波包分解和混沌振子的小电流接地系统故障选线[J].电工技术学报,2015(3):13-20. [9] 贺家李,宋从矩.电力系统继电保护原理[M].北京:中国电力出版社,2004:58-66. [10] 刘万顺,黄少峰,徐玉琴.电力系统故障分析[M].北京:中国电力出版社,2010:332-336. [11] 要焕年,曹梅月.电力系统谐振接地[M].北京:中国电力出版社,2009: 64-69. [12] 薛永端,李娟,徐丙垠 等.中性点不接地系统小电流接地故障暂态等值电路的建立[J].中国电机工程学报,2013,33(34):223-232. [13] 薛永端,李娟,徐丙垠,等.中性点经消弧线圈接地系统小电流接地故障暂态等值电路及暂态分析[J].中国电机工程学报,2015,35(22):5703-5714. (责任编辑杨继森) TheTransientNetworkinNon-SolidlyEarthedNetworksbyVectorGroupsMethodandPrincipalComponentsAnalysis SUN Runcheng, ZHAO Hongwei, MENG Qingwu, TIAN Zhigang, LIU Guosong (Department of Machinery & Electrical Engineering, Logistic Engineering University, Chongqing 401311, China) For traditional vector method does not apply in the transient process, a network simplification principle, which express the transient electric parameters in vector groups with multiple frequency and amplitude, is proposed. By the way of eliminating some nodes of node voltage equation and adding the grounding currents of bus and the load neutral point, a simplified transient network is established in which the voltages are compensated by controlled sources. Simulation results show that the simplified transient network has higher accuracy and stronger adaptability comparedwith the traditional one. non-solidly earthed networks; vector group; nodal voltage equation; constraint equation 2017-04-20; :2017-05-22 孙润诚(1993—),男,硕士研究生,主要从事电力系统运行与控制研究。 10.11809/scbgxb2017.09.025 format:SUN Runcheng, ZHAO Hongwei, MENG Qingwu, et al.The Transient Network in Non-Solidly Earthed Networks by Vector Groups Method and Principal Components Analysis[J].Journal of Ordnance Equipment Engineering,2017(9):121-125. TM77 :A 2096-2304(2017)09-0121-05 本文引用格式:孙润诚,赵宏伟,孟庆武,等.基于向量组法的小电流接地故障暂态网络建立[J].兵器装备工程学报,2017(9):121-125.




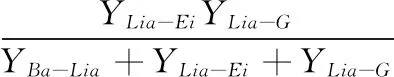
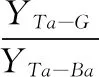

3 仿真验证


4 结论
