含区间参数的柔性弹箭特征值分析

舒睿洪,王国平，武令伟

(南京理工大学 能源与动力工程学院， 南京 210094)

【装备理论与装备技术】

含区间参数的柔性弹箭特征值分析

舒睿洪,王国平，武令伟

(南京理工大学 能源与动力工程学院， 南京 210094)

系统结构参数的随机性会引起系统振动特性的变化；基于区间参数和多体系统传递矩阵法，分析了火箭弹特征值问题，并对含区间参数的柔性火箭弹振动特性进行了数值仿真，进而比较了弹长、弹重和转动惯量的波动对振动特性的影响以及推力和质量流失对横向位移的影响；该方法涉及的矩阵阶次低，计算速度快，无需建立系统总体动力学方程，为研究复杂变截面弹箭和飞行中的复杂问题提供了重要参考。

传递矩阵法；柔性弹箭；特征值；振动特性

多管火箭武器系统具有机动性好、成本低、威力大，可在较短时间对面目标进行强火力攻击，在战场上具有非常重要的地位。它的射击精度和密集度，都会受到火箭弹振动特性的影响，因此，含不确定区间参数的柔性弹箭振动分析[1-4]，对于火箭弹的研究具有重要意义。但在生产制造过程中，由于各材料特性、制造工艺、装配过程和具体使用等多种因素的影响，导致弹箭系统的各参数具有随机性，而结构参数的随机性会导致系统振动特性变化。因此，对含区间参数的柔性弹箭特征值[5]的分析已引起研究人员的关注。目前解析法、Monte Carlo法以及摄动法是最常用的3种弹箭振动特性的研究方法。但一般力学方法在分析柔性体固有振动特性时，常会面临解决矩阵阶次高、计算量繁复等问题。董满才等[6]基于多体系统传递矩阵法，分析比较了这3种方法的优劣。戎保等[7]在传递矩阵法和摄动法的基础上，分析了参数变化造成火箭弹振动特性的变化。本文利用多体系统传递法，分析细长的柔性弹箭在飞行过程中的固有振动特性，并通过单一变量法依次研究各初始参数在相应区间内对该柔性弹箭固有振动特性中的频率、振型、响应以及横向位移的影响。

本课题基于区间参数[8]和多体系统传递矩阵法理论[9-10]，通过对弹箭系统动力学模型的建立，利用动力学理论推导了传递方程和传递矩阵，进行了特征值分析，进而比较弹长、弹重和转动惯量的波动对振动特性的影响以及推力和质量流失对振动横向位移的影响。该方法涉及的矩阵阶次低，计算速度快，无需建立系统总体动力学方程，为研究复杂变截面弹箭和飞行中的复杂问题提供了重要参考。

1 求频率以及固有振型

随着火箭弹射程和性能的提高，其长细比逐渐变大，当火箭弹长细比达到25以上时，对其固有振动特性的分析时需要将其作为柔性体处理。为叙述方便，假设该柔性弹振动符合以下基本假设： 柔性弹为沿弹轴截面变化的梁，且弹体中心线与质量中心线重合； 长径比大，不考虑剪切的影响； 轴向刚度远大于横向弯曲刚度，忽略拉压变形的影响。

在物理坐标系下定义输出点O与输入点I的状态矢量为

(1)

式(1)中状态矢量见参考文献[11]。因此系统自由振动时有

(2)

式(2)中ω为火箭弹的固有频率。模态坐标系下输出点O(即弹头)和输入点I(即弹尾)的状态矢量分别为

(3)

根据弹头弹尾传递关系可得矩阵：

ZO=UZI

(4)

式(4)系统的传递矩阵：

(5)

将边界条件

代入式(4)可得特征方程

(6)

解此方程便可得系统的固有频率。由于超过10阶后对特征方程组的影响忽略不计，因此对所求得的频率只求前10阶。每一阶固有频率求特征方程组：

(7)

便可求得火箭弹弹头处的状态矢量。再通过传递方程即可求得火箭弹长方向任意位置的系统振型和状态矢量。火箭弹前10阶具体振型如图1所示，其最值及频率如表1。

由图1和表1可看出，振动周期随着频率的增加而减小；振幅随着频率的增大而减小，第10阶的振幅已衰减到第一阶振幅的0.15，且相邻两个频率值相差越小，振幅变化越大，振型图中的最大值逐渐减小。

表1 火箭弹前10阶振型最值及频率

2 动力响应

多刚柔体系统无阻尼的体动力学方程为

Mvtt+Kv=f

(8)

根据动力响应物理坐标在增广特征矢量Vk下展开可得

(9)

用增广特征矢量求内积，同时应用增广特征矢量正交性得

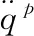
(10)

设该柔性弹系统的初始条件为

(11)

则

(12)

在广义坐标的解的基础上可得火箭弹的动力响应为

(13)

模态质量

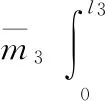
火箭弹X方向位移为

(14)

Y方向位移为

(15)

由于火箭弹是轴对称的，Z轴振动情况和Y轴一致，仅讨论Y轴方向。

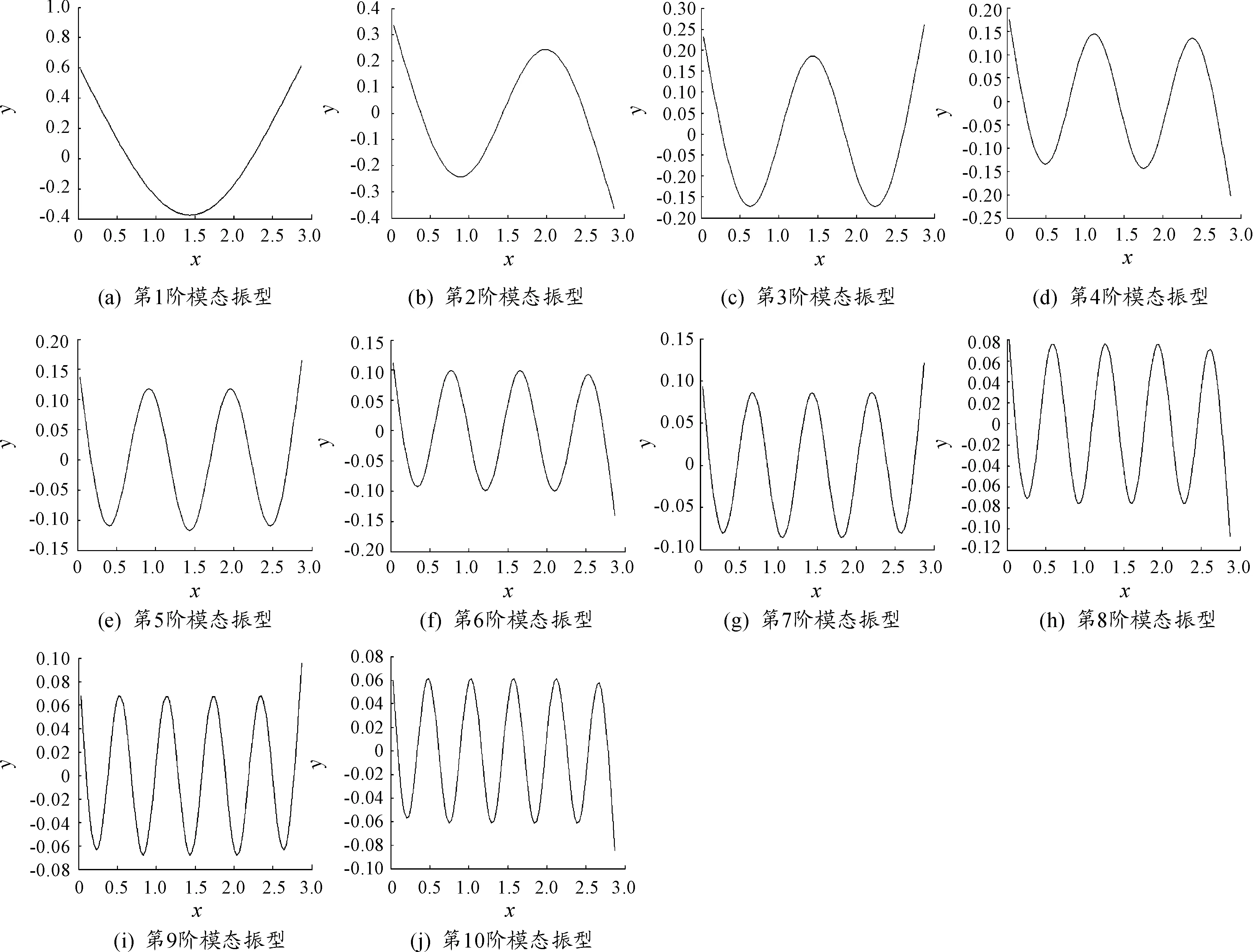
图1 火箭弹前10阶振型

火箭弹在燃料燃烧过程中推力保持不变，但由于燃料不断燃烧，火箭弹质量流失的振动位移时间历程如图2(a)、图2(b)所示，在燃料完全燃烧后，火箭弹质量基本保持不变的情况下的振动位移时间历程如图2(c)、 图2 (d)所示。

图2(c),图2(d)是火箭弹在只受重力情况下，X、Y方向的振动位移时间历程。实验表明，火箭弹在飞行过程中燃料燃烧时间为2s，图2 (a)、 图2 (b)是飞行过程中的振动位移时间前两秒，在推力一定的情况下，质量不断流失，2 s后只受重力和空气阻力。从图中可看出，和飞行过程中相比，只受重力影响的情况下X、Y方向振动位移明显小很多，说明推力和空气阻力对振动所产生的横向位移影响较大。并且，随着质量减少，产生的横向振动位移振幅减小，振动周期大幅度增加。

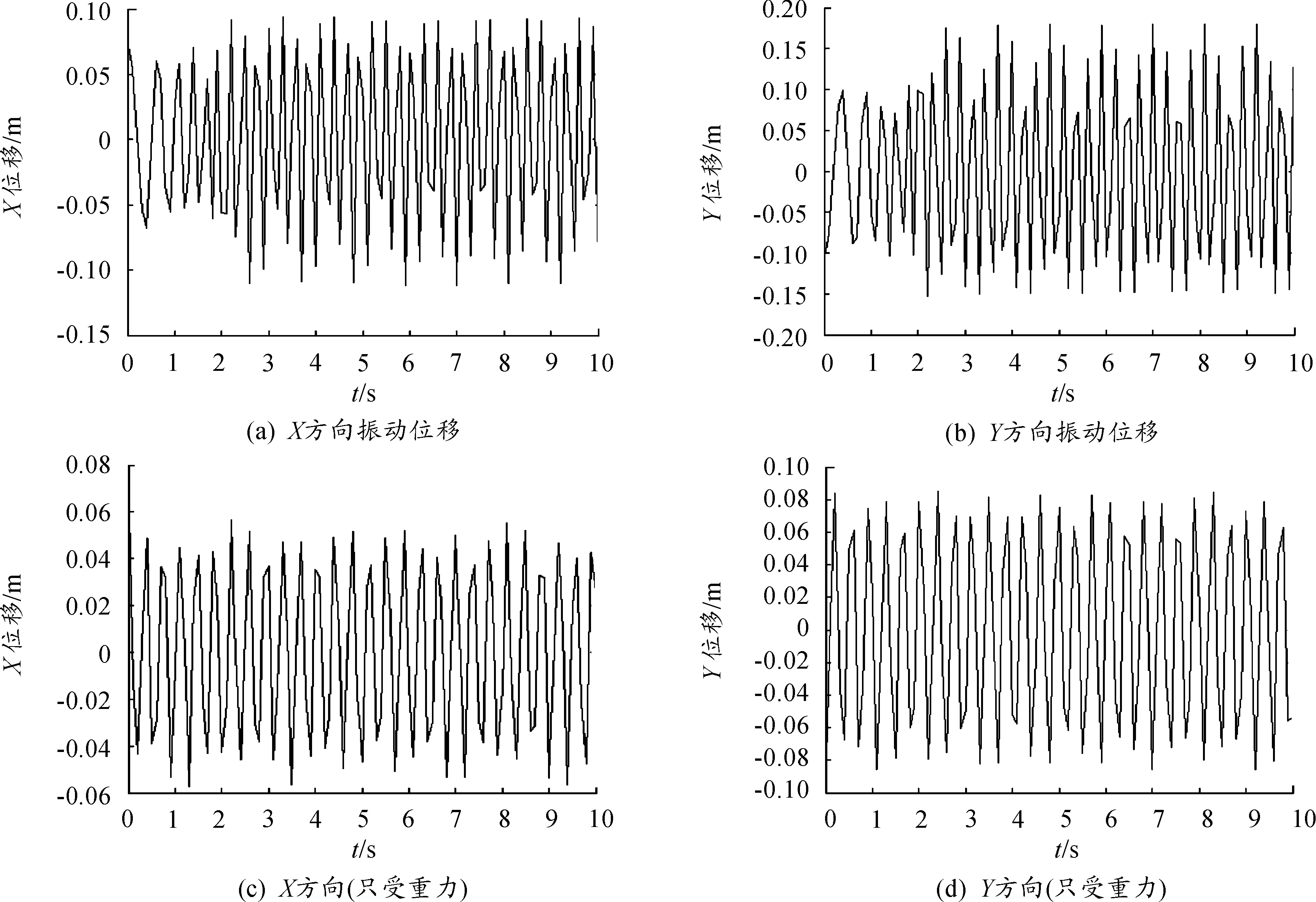
图2 位移时间历程

3 参数变化对振动的影响

由于材料、加工以及装配等问题，火箭弹的弹长、弹重和转动惯量实际值都会在理论值附近的区间波动。随着机械加工精度的提高，火箭弹的长度和质量的加工误差相对较低，通常能控制在上下5%的范围以内，但转动惯量装配过程中会产生二次误差，使最终的误差范围在上下10%的范围内。为了研究区间参数对火箭弹的振动特性的影响，使弹长、弹重在标准值上下5%的范围、转动惯量在上下10%范围内单独变化以及3个变量同时变化，分别计算了火箭弹前10阶固有振动频率，并分析单一变量和3个变量同时变化时对固有频率的影响效果，具体变化分析示意图如图3、图4、图5和图6所示。

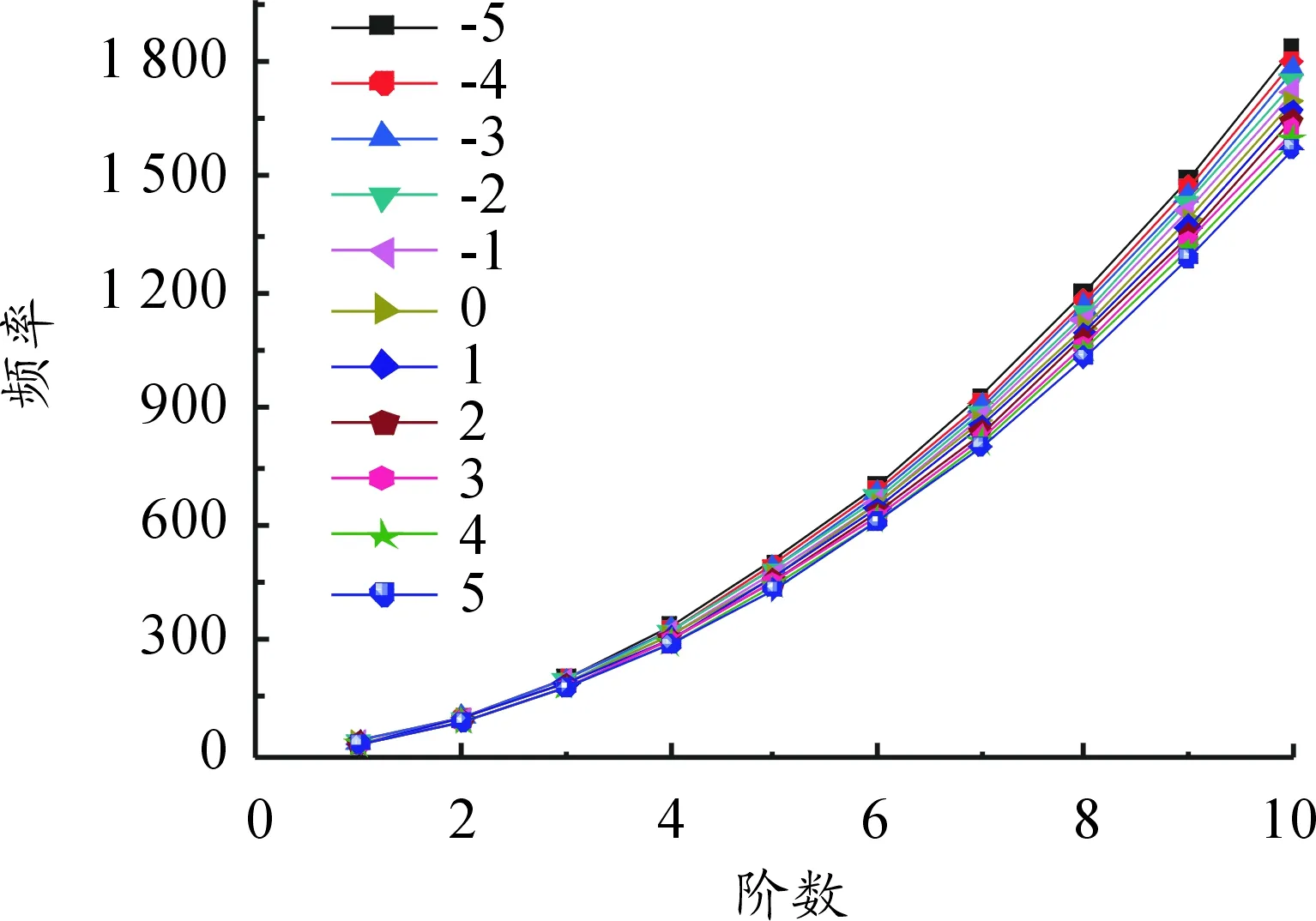
图3 频率随长度变化

图4 频率随质量变化

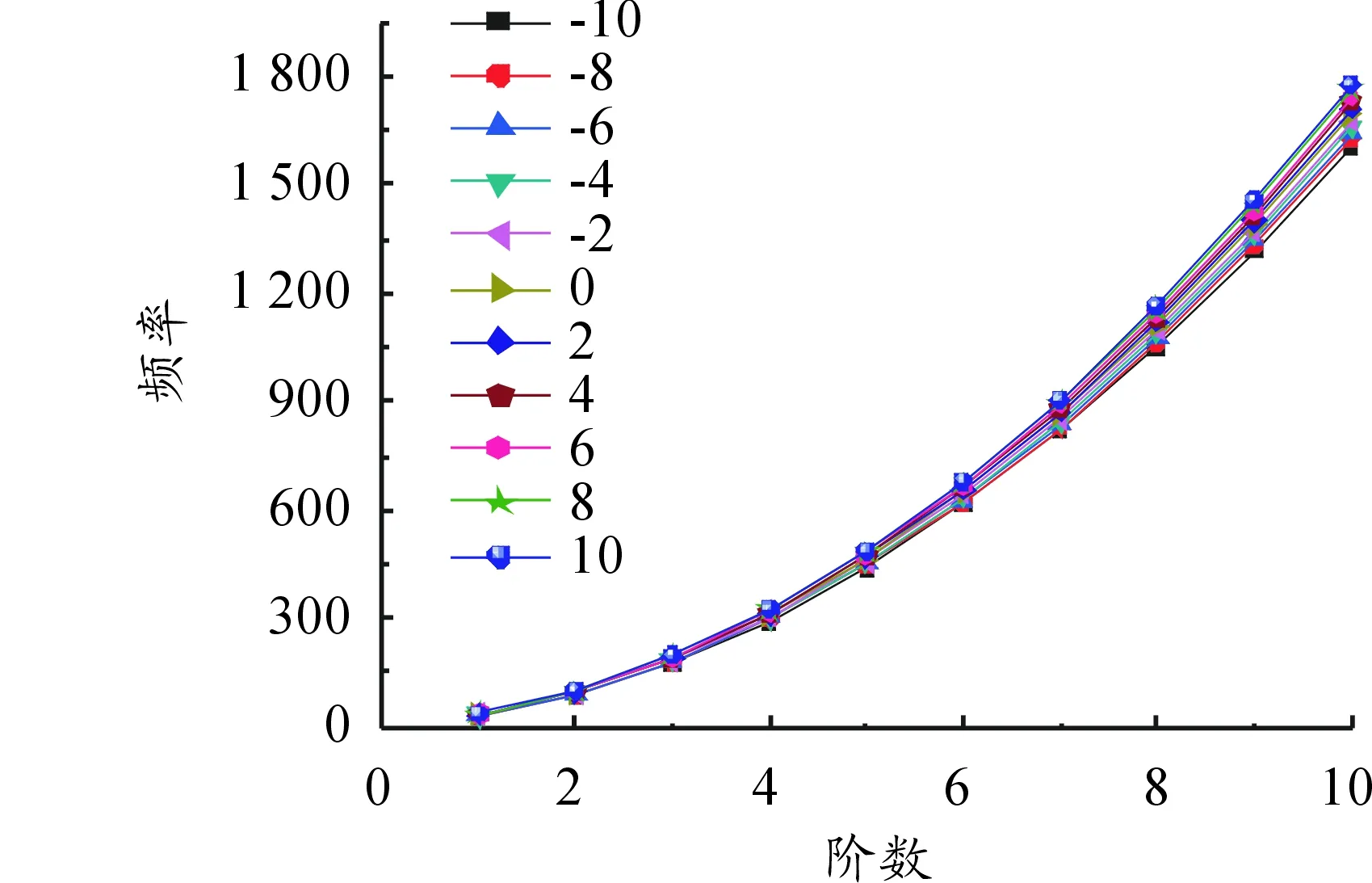
图5 频率随转动惯量变化

图6 频率随质量、弹长、转动惯量同时在区间变化

由此可知，随着弹长、弹重和转动惯量分别在标准值上下5%区间范围内变化时，弹箭的固有振动频率值分别随弹长和弹重的增加而减小，随着转动惯量的增加而增加，但长度对频率的影响最为显著。由图5可知，当弹重、弹长和转动惯量同时在区间范围内变化时，对频率的影响大于3个变量分别作用时对频率的影响，可见三者对频率的作用会相互影响。

由图3可知，随着长度增加，频率减小；长度在标准值5%范围内波动时，第一阶变化7.51%，到第10阶变化7.56%，可得出高阶情况下长度对频率影响范围略小。由图4可知，随着质量增加，频率减小。由图5可知，各阶振动频率随着转动惯量的增加而增加，且转动惯量对高阶的频率变化略多于低阶，推力和空气阻力对振动所产生的横向位移影响较大。并且，随着质量减少，产生的横向位移振幅减小，振动周期大幅度增加。

4 结论

本文采用了区间参数和多体系统传递矩阵法分析了柔性火箭弹的随机特征值问题。该方法无需建立系统总体动力学方程，涉及的矩阵阶次低，可快速获得精度较高的全系统固有振型，在一定程度上保证了柔性火箭弹特征值的快速计算，并成功分析出弹长、弹重和转动惯量对火箭弹振动特性的影响。该研究将为更加复杂的变截面火箭弹的研究分析以及实际飞行过程中遇到的更加复杂的问题提供参考。

[1] 芮筱亭,王国平,陈卫东.多管火箭随机发射与飞行动力学仿真[J].南京理工大学学报,2003,27(5):616-620.

[2] 展志焕,芮筱亭,戎保.多管火箭定向管振动控制设计[J].振动工程学报，2011，24(3):327-332.

[3] 芮筱亭,戎保.多体系统传递矩阵法研究进展[J].力学进展，2012，42(5):4-17.

[4] 展志焕,芮筱亭,王国平.基于多体系统传递矩阵法的多管火箭定向管振动控制[J].力学学报，2010，42(3):583-590.

[5] 赵锐.时变质量柔性结构的动力学建模与分析[D].哈尔滨：哈尔滨工业大学,2012.

[6] 戎保,芮筱亭,王国平,等.参数不确定性细长火箭弹随机特征值问题研究[J].工程力学,2012(7):341-346.

[7] 何斌,芮筱亭,于海龙.细长弹箭固有振动特性分析有限元传递矩阵法[J].动力学与控制学报,2005(4):66-70.

[8] 王良明.大长径比弹箭在飞行时的柔性变形特性分析[J].兵工学报,2000,21(2):108-111.

[9] 展志焕,芮筱亭,王国平.基于多体系统传递矩阵法的多管火箭定向管振动控制[J].力学学报，2010，42(3):583-590.

[10] 何斌.多体系统传递矩阵法研究及其在发射动力学中的应用[D].南京：南京理工大学,2006.

[11] 芮筱亭,贠来峰,陆毓琪,等.多体系统传递矩阵法及其应用[M].北京:科学出版社,2008.

(责任编辑周江川)

ResearchonEigenvalueswithIntervalParametersofFlexibleMissile

SHU Ruihong, WANG Guoping, WU Lingwei

(School of Energy And Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

On the basis of interval parameter and multi-body system transfer matrix method, this paper not only analyzes the problem of eigenvalue of rocket, but also carries out the numerical simulation of the flexible rocket vibration characteristics with interval parameters. And then the influence of the fluctuation of the bomb length, the bomb weight and the moment of inertia on the vibration characteristics and the influence of the thrust and mass loss on the lateral displacement are compared. Involving a low order of the matrix and computing fast, this way has no need to establish the overall system dynamics equation and provides an important reference for the study of complex variable cross-section projectile and flying complex problems.

transfer matrix method; flexible missile; eigenvalues; vibration characteristics

2017-04-24；

：2017-05-25

舒睿洪(1994—)，女，主要从事弹箭外弹道研究。

王国平(1976—)，男，研究员，主要从事武器系统动力学控制与优化设计研究。

10.11809/scbgxb2017.09.010

format:SHU Ruihong, WANG Guoping, WU Lingwei.Research on Eigenvalues with Interval Parameters of Flexible Missile[J].Journal of Ordnance Equipment Engineering,2017(9):48-52.

TJ513

：A

2096-2304(2017)09-0048-05

本文引用格式：舒睿洪,王国平，武令伟.含区间参数的柔性弹箭特征值分析[J].兵器装备工程学报，2017(9):48-52.