逐步增加的Ⅱ型截尾寿命试验下BS分布的统计分析

佘纪涛，徐晓岭，顾蓓青

(上海对外经贸大学 统计与信息学院， 上海 201620)

【机械制造与检测技术】

逐步增加的Ⅱ型截尾寿命试验下BS分布的统计分析

佘纪涛，徐晓岭，顾蓓青

(上海对外经贸大学 统计与信息学院， 上海 201620)

在逐步增加的Ⅱ型截尾寿命试验场合下，研究两参数Birnbaum-Saunders(简称BS)疲劳寿命分布产品的可靠性统计分析似然函数，运用泰勒展开得到了近似似然方程，通过求解仅含刻度参数的超越方程得到形状参数的近似极大似然估计；最后通过Monte-Carlo模拟算例说明方法的可行性。

两参数Birnbaum-Saunders疲劳寿命分布，逐步增加II型截尾，近似极大似然估计

在可靠性试验中，逐步增加的Ⅱ型截尾寿命试验在实际中经常碰到，具有理论与应用价值。譬如当组织一批价值昂贵的产品做寿命试验，若已发生一部分产品失效时，考虑到试验费用等因素，经常从未失效的产品中抽取一部分产品移离试验现场，这样可以大大节约成本。又例如在寿命试验过程中为了解产品的失效机理和退化情况，以便更好设计产品，需要从尚未失效的产品中选取部分产品进行解剖分析。关于逐步增加的II型截尾寿命试验的统计分析可见文献[1-6]，其主要针对的是威布尔与对数正态等寿命分布。

Birnbaum-Saunders(简称BS)模型是概率物理方法的一个重要失效分布模型，这个模型是Birnbaum和Sauders在1969年研究主因裂纹扩展导致的材料失效过程中推导出来的，这一模型在机械产品可靠性研究中应用广泛，主要应用于疲劳失效研究，对于电子产品性能退化失效分析也有重要应用。Birnbaum-Saunders疲劳寿命分布比常用寿命分布如威布尔分布,对数正态分布更适合描述某些由于疲劳而引起失效的产品寿命规律，因此该分布已经成为可靠性统计分析中的常用分布之一。关于Birnbaum-Saunders疲劳寿命的统计分析研究可见文献[7-18]，其中关于统计分析的研究大多是全样本场合，而针对Birnbaum-Saunder疲劳寿命分布逐步增加的Ⅱ型截尾寿命试验的统计分析至今未见文献报导。

逐步增加的Ⅱ型截尾试验是Ⅱ型截尾试验的一个推广，它是在n个产品的样本中先观察到r1个失效，然后剩下的n-r1个未失效的产品中有n1个被移离试验，留下n-r1-n1个产品继续试验；当再有r2-r1个产品失效后,将剩余仍未失效产品中的n2个被移离试验。试验如此进行下去，直到有一定数量的产品失效为止，终止试验。试验数据如表1所示，其中r0=0,n0=0,x(0)=0,ri≥1,ni≥0,i=1,2,…,k,k≥1，而nk为最后试验结束时未失效的产品数。当ni=0,i=1,2,…,k-1时，便为通常的定数截尾寿命试验；当r1=1,r2=2,…,rk=k时，通常称为逐次截尾实验。

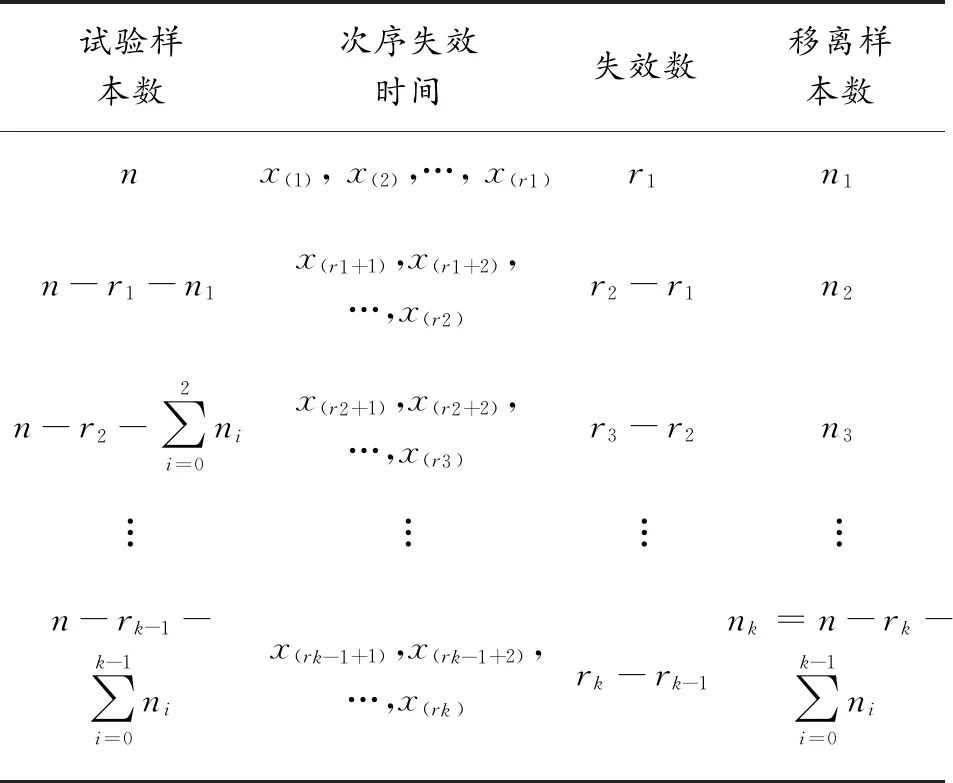
表1 逐步增加的Ⅱ型截尾寿命试验数据

本文给出两参数Birnbaum-Saunders疲劳寿命分布在逐步增加Ⅱ型截尾寿命试验下的近似极大似然估计，并通过实例分析说明该方法的应用可行。

1 两参数Birnbaum-Saunders疲劳寿命分布参数的近似极大似然估计

将n个寿命服从两参数Birnbaum-Saunders疲劳寿命分布(记为BS(α,β))的产品做逐步增加的Ⅱ截尾寿命试验，试验数据如表1所示。而两参数BS(α,β)分布函数FX(x)与密度函数fX(x)分别为

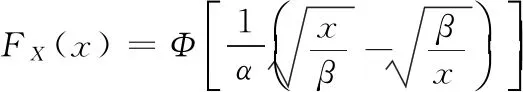
x>0,α,β>0

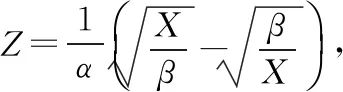
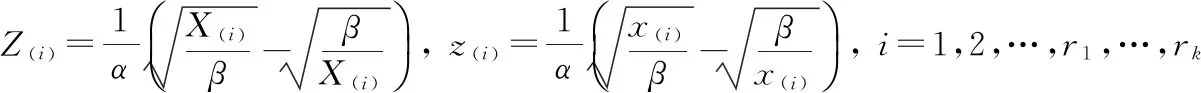
易见

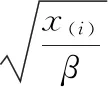
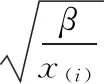
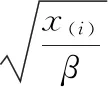
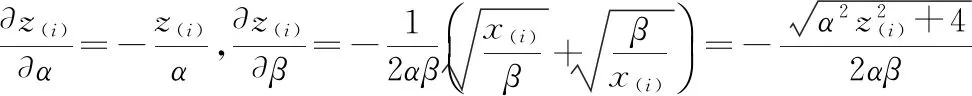
FX(x)=Φ(z)

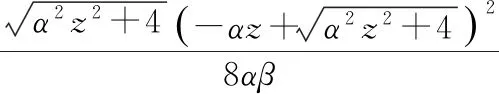
而

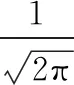
似然函数：

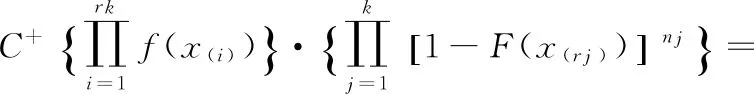
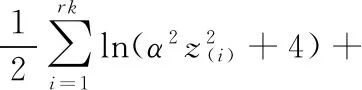
注意到

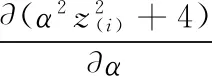
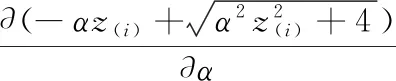
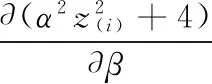
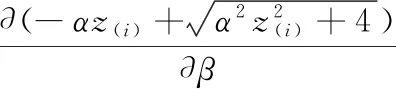
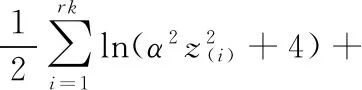
(1)

(2)

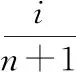
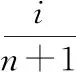
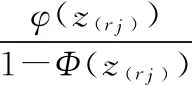
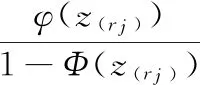
(3)

将式(3)代入式(1)得：

化简得：

即

α2-H(β)α-Q(β)≈0

(4)

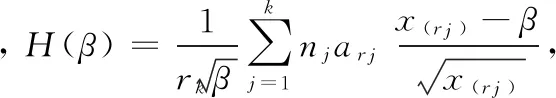
将式(3)代入式(2)得：

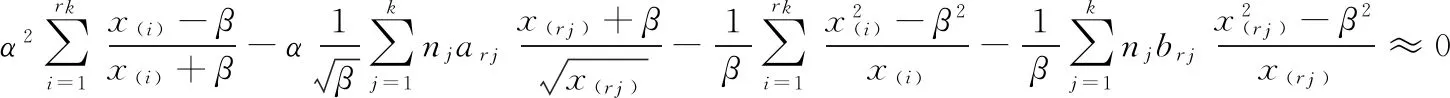
于是得如下方程：

α2-G(β)α-L(β)≈0

(5)

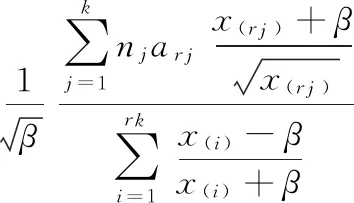
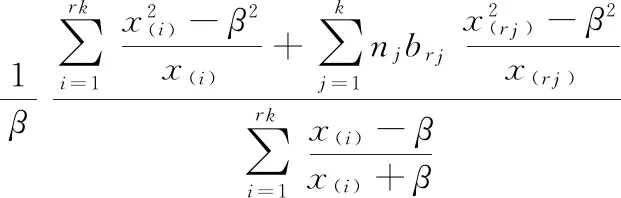
由此可得：

(6)

进而可得仅含参数β的超越方程：

[Q(β)-L(β)]2-H(β)[Q(β)-L(β)][G(β)-H(β)]-

Q(β)[G(β)-H(β)]2≈0

(7)

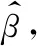
(8)

再者

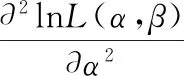
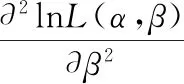
其中，

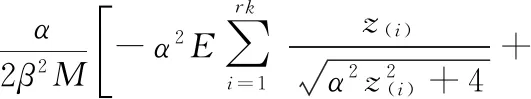
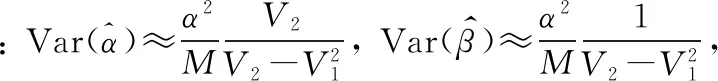
2 实例分析

例[19]：某种轴承的疲劳寿命，共10个数据(单位：小时)：

152.7， 172.0， 172.5， 173.5， 193.0， 204.7，

216.5， 234.9， 262.6， 422.6

先保留前5个数据，后按照随机原则删掉2个数据(删掉234.9和262.6)后，留下3个数据(204.7，216.5，422.6)，利用本文方法可以得到参数的近似极大似然估计为

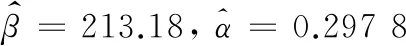
作为比较，文献[19-20]利用全样本数据得到如下6种点估计，见表2所示。

表2 全样本场合下参数β,α的6种点估计

3 结论

介绍了在逐步增加的II型截尾寿命试验条件下BS疲劳寿命分布产品的可靠性统计分析似然函数。及得到近似似然方程和形状参数的近似极大似然估计的推导过程，通过实际算例说明了方法实用可行。

[1] 徐晓岭，王蓉华.Weibull分布逐步增加的Ⅱ型截尾试验的统计分析[J].强度与环境，2003，30(2)：31-37.

[2] 王炳兴.Weibull分布基于定数逐次截尾寿命数据的统计分析[J].科技通报，2004，20(6)：488-496.

[3] 李凤，师义民，田亚爱.逐步增加II型截尾下Weibull分布的Bayes估计[J].工程数学学报，2008，25(4)：641-650.

[4] 卫超，师义民.逐步Ⅱ型混合截尾下Pareto分布的统计分析[J].火力与指挥控制，2014，39(4)：27-33.

[5] 杨君慧，师义民，曹弘毅.逐步增加Ⅱ型截尾试验下广义指数分布的统计分析[J].统计与决策，2014(16)：28-30.

[6] BALAKRISHNAN N A.Clifford Cohen.Order Statistics and Inference Estimation Methods[M].Boston:Academic Press,1991.

[7] KUNDU D,KANNAN N,BALAKRISHNAN N.On the hazard function of birnbaum-saunders distribution and associated inference[J].Computational Statistics & Data Analysis,2008,52:2692-2702.

[8] WANG Ronghua,FEI Heliang.Statistical analysis for the birnbaum-saunders fatigue life distribution under multiply type II censoring[J].Chin Quart of Math,2006,21(1):15-27.

[9] WANG Ronghua,FEI Heliang.Statistical analysis for the birnbaum-saunders fatigue life distribution under type II bilateral censoring and multiply type II censoring,chin.quart[J].J of Math,2004,19(2):126-132.

[10] 孙祝岭.Birnbaum-Saunders 疲劳寿命分布尺度参数的区间估计[J].兵工学报，2009，30(11)：1558-1561.

[11] 孙祝岭.Birnbaum-Saunders 疲劳寿命分布参数的回归估计方法[J].兵工学报，2010，31(9)：1260-1262.

[12] 孙祝岭.疲劳寿命分布变异系数的统计推断[J].质量与可靠性，2013(1)：13-15.

[13] 孙祝岭.Birnbaum-Saunders分布环境因子的置信限[J].强度与环境，2012，39(4)：51-55.

[14] WANG Bingxing.Generalized interval estimation for the birnbaum-saunders distribution[J].Computational Statistics and Data Analysis,2012,56:4320-4326.

[15] NIU Cuizhen,GUO Xu,XU Wangli,et al.Comparison of several birnbaum-saunders distributions[J].Journal of Statistical Computation and Simulation,2014,84(12):2721-2733.

[16] 赵建印,孙权,彭宝华,等.基于加速退化数据的BS分布的统计推断，电子产品可靠性与环境试验，2006(1)：11-14.

[17] BALAKRISHNAN N,ZHU Xiaojun Zhu,On the existence and uniqueness of the maximum likelihood estimates of the parameters of birnbaum-saunders distribution based on type-I,type-II and hybrid censored samples[J].Statistics,2014，48(5)：1013-1032.

[18] 徐晓岭,王蓉华,顾蓓青.关于两参数Birnbaum-Saunders疲劳寿命分布统计分析的2个注记[J].浙江大学学报(理学版)，2016，43(5)：539-544.

[19] NG H K T,KUNDU D,BALAKRISHNAN N.Modified moment estimation for the two-parameter birnbaum-saunders distribution[J].Computational Statistics and Data Analysis,2003,43:283-298.

[20] SYED E.Ahmed,kamon budsaba,supranee lisawadi,andvei volodin,parametric estimation for the birnbaum-saunders lifetime distribution based on a new parametrization[J].Thailand Statistician July,2008,6(2):213-240.

(责任编辑唐定国)

StatisticalAnalysisofBSDistributionUnderProgressiveType-ⅡCensoredLifeTest

SHE Jitao, XU Xiaoling, GU Beiqing

(School of Statistics and Information, Shanghai University of International Business and Economics, Shanghai 201620, China)

The reliability statistical analysis method of two parameters Birnbaum-Saunders (BS) fatigue life distribution products is studied under progressive type-II censored life test. The likelihood function is given, and the approximate likelihood equation is obtained by Taylor expansion. By solving the transcendental equation with only scale parameter, we get approximate maximum likelihood estimation of shape parameter. Finally, the examples illustrated the feasibility of the method by Monte-Carlo simulations.

two-parameter Birnbaum-Saunders fatigue life distribution; incremental type II truncated censoring; approximate maximum likelihood estimation

2017-05-12；

：2017-05-30

：2017年上海市大学生创新创业训练计划项目(102732017093)；国家自然科学基金资助项目(11671264)

佘纪涛 (1995—)，女，主要从事应用统计研究。

10.11809/scbgxb2017.09.033

format:SHE Jitao, XU Xiaoling, GU Beiqing.Statistical Analysis of BS Distribution Under Progressive Type-Ⅱ Censored Life Test[J].Journal of Ordnance Equipment Engineering,2017(9):156-160.

O251

：A

2096-2304(2017)09-0156-05

本文引用格式：佘纪涛，徐晓岭，顾蓓青.逐步增加的Ⅱ型截尾寿命试验下BS分布的统计分析[J].兵器装备工程学报，2017(9):156-160.