多种属性选取标准“多数表决”优化决策树研究

王森，赵发勇，陈曙光

（阜阳师范学院物理与电子工程学院，安徽阜阳236037）

多种属性选取标准“多数表决”优化决策树研究

王森，赵发勇，陈曙光

（阜阳师范学院物理与电子工程学院，安徽阜阳236037）

测试属性的选取即属性选择标准是构建决策树的关键及核心，对于同样的数据集，不同的属性选取标准构建的决策树有可能差别很大。对于不知采用何种属性选择标准或者没有一种标准适合所处理的数据集，本文提出了一种解决的方法，即多种属性选取标准多数表决优化决策树算法，该算法利用“专家会诊”的思想，构建决策树，具有更广的适应性和更可能高的准确率。

属性选取标准；多数表决；决策树

在创建决策树过程中，测试属性选取标准非常重要，可以说处于核心和最重要的地位，而如何选择好的测试属性或属性值的逻辑判断是构建好的决策树的关键。对于相同的训练数据集，可以采用不同的算法构建符合这个训练数据集决策树。不同的算法构建的决策树可能相同，也可能不同。研究表明，一般情况下，构建的决策树越简单，预测能力越强[1]。要构造尽可能简单的决策树，关键在于选择合适的测试属性或产生合适的逻辑判断式的标准。针对不同特性的数据集，人们提出了多种不同测试属性选择标准（如信息增益标准[2]、信息增益率标准[3]、基于距离度量的标准、G统计标准、Gini-index标准[4]、基于χ2统计的标准[4]、最小描述长度标准、基于相关度的标准等等）。不同的度量标准，有不同的效果，特别是对于多值属性，选择不同的度量标准对于结果的影响很大，也有许多学者提出一些改进的方法[5-11]来选取测试属性。对于用户来说，选择哪种标准确实比较困难，往往要根据经验或领域知识来确定，或经过多种标准的构建的决策树进行比较（如预测的准确率、构建决策树的效率等方面），选择最符合实际的需要的决策树，用于未来的决策。

在面对一个数据集时，不知采用何种属性选择标准对分类比较准确、或者哪种属性选取标准都不理想时，就像同一病人，不同的医生可能诊断结果不同，或者任何一个医生治疗的效果都不好时，可能要专家会诊，这样不同的医生可以从不同的角度对病人提出不同的治疗意见，为了达成一致的意见，往往要进行多数表决，在票数相同时，听取有名专家的意见。受这种思想的启发，我们在构建决策树时，在进行属性选择时，采用多个不同属性选择标准来选择测试属性，最终采用多数表决方法来决定哪个是最终的测试属性，即票数最多的作为测试属性（或分裂属性），若票数最多的属性有多个时，采用最有影响的属性选择标准（如ID3的信息增益或者C4.5系统的信息增益率标准）所选择的属性作为测试属性。文中选择信息增益标准、信息增益率标准、Gini-index标准和χ2统计标准作为属性选择标准，采用多数表决的方式来优化构建决策树，在票数相同时采用信息增益率标准选择的测试属性作为最终要选取的测试属性来构建决策树。

1 测试属性选择标准简介

这里，假设训练数据样本的集合S中有s个数据样本。假定类别属性C，有m个不同值，即Ci(i=1,2,…,m)。在类Ci中有数据样本si个。

1.1 信息增益标准

经典的ID3算法使用该标准，对要学习的一个训练样本集，类别属性的信息熵由下式给出：

其中，pi是任意样本属于类Ci的概率，并用sis近似估计。

根据属性A划分成子集的熵由下式给出：

其中，m是类别属性值的个数，n是候选属性A的取值个数；熵值越小，说明训练样本集根据属性A划分的子集纯度越高。

根据属性A的值划分训练样本集的信息增益是：

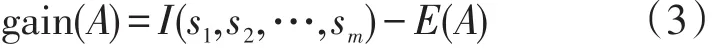
计算并比较各候选属性的信息增益，选取信息增益最大的候选属性作为测试属性，并以该测试属性创建一个结点并标记此结点，再根据该测试属性的每个值划分样本并为每一个划分产生一个分枝。算法以递归的方法自上而下在每个被划分的数据样本集中进行同上操作，直到被划分的每个集合属于同一个类别为止；否则算法选择具有不同类的子集递归进行同上操作。

1.2 信息增益率标准

C4.5系统使用该标准，信息增益率是在信息增益的基础之上发展起来的，它避免信息增益的多值趋向，是对信息增益的优化。通过计算并比较各候选属性的信息增益率，信息增益率最大候选属性被选择作为测试属性。具体过程：首先，通过公式（1）、（2）和（3）计算各侯选属性的信息增益，然后根据如下公式（4），计算各候选属性的信息增益率。用于对候选属性A的信息增益率计算的函数定义如下：

1.3 Gini-index标准

Gini-index是一种度量不纯度的函数，CART算法变形使用该标准，在Gini-index标准中用Gini-index指数来度量训练数据集中各侯选属性划分类别属性的“纯度”。

若训练样本集中各个类别是均匀的，则该训练数据集具有最大的不纯度，否则，如果训练样本在各类别中数量差距很大，则训练数据集的不纯度就较小；如果训练样本同属性一个类别，则为0。

假设不纯度函数φ定义在一个k元组((p(c1),p(c2),…,p(ck))上，则不纯度函数φ满足下列条件：

由于根据各属性的不同取值对训练数据集进行划分，数据集合变的越来越小，这将导致平均训练数据集的不纯度的减小（即纯度增加）。在该标准中，作为不纯度函数形式如下：

其中，p(ci)≥0（i∈{1,2,…,k}）表示每个类别在训练数据集中的概率。

把Gini-index应用在决策树中，则节点t的不纯度函数为：

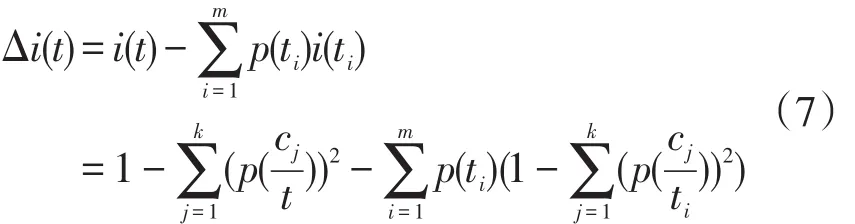
其中，假定结点t所对应的候选属性有m个取值，则根据该候选属性值划分训练数据集，则对应的得到m个数据子集t1,t2,…,tm，而每个数据子集所占训练数据集的比例分别为p(t1),p(t2),…,p(tm)。

在具有Gini-index标准的算法中，首先计算并比较各候选属性划分样本带来的纯度增量；选取使纯度增量最大的候选属性作为测试属性，并据此划分训练数据集；最后在每个划分后的子集中，递归进行上面的纯度增量计算并划分。

1.4 χ2统计标准

CHILD算法变形使用该标准，χ2统计是用基于统计学的方法，通过统计分析各侯选属性与类别属性关联程度，选取关联程度最大的属性作为测试属性。一般步骤如下：首先用列联表表示侯选属性与类别属性的取值频率；其次比较它们实际观察到的频率与假设在没有关联的情况下的频率，得到近似于χ2统计的统计量的分布。χ2统计标准的基本方程为：

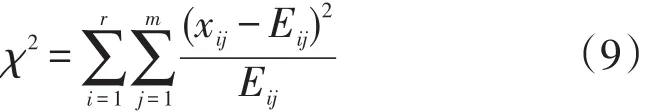
假设一个训练数据集中含有候选属性A和类别属性C，由它们所构成的列联表如表1所示，其中，xij表示训练数据集中候选属性A取值Ai类别属性C取值Cj的训练样本的个数；xoj表示类别属性C取值Cj的训练样本总数，统计量xio表示候选属性A取值Ai的训练样本总数。

表1 属性A和分类属性C的列联表

χ2统计标准通过计算并比较类别属性与各候选属性的关联程度，选取关联程度最大的候选属性作为测试属性或分裂属性。

2 多种属性选取标准多数表决决策树算法

由基本理论基础，构建多种属性选取策略优化决策树算法如下：

算法：Gen_Multi_Sta_Dec_Tree由给定训练数据集产生一棵多种属性选取标准多数表决决策树。

输入：由离散属性表示的训练数据集S，和用于构建决策树的候选属性集合A。

输出：一棵多种属性选取标准多数表决决策树。

步骤：

①采用ID3标准计算并比较各候选属性的信息增益值，并使信息增益最大的候选属性被选次数增一。

②采用C4.5标准计算并比较各候选属性的信息增益率，并使信息增益率最大的候选属性的被选次数增一。

③采用Gini_index标准计算并比较各候选属性的纯度增量，并使纯度增量最大的候选属性的被选次数增一。

④采用χ2统计标准计算并比较各候选属性与类别属性关联程度，并使关联程度最大的候选属性的被选次数增一。

3 具体示例

本文给出了取自AllElectronics顾客数据库数据元组训练集（数据取自[Qui86]）如表2，对构建多决策判定树过程如下：

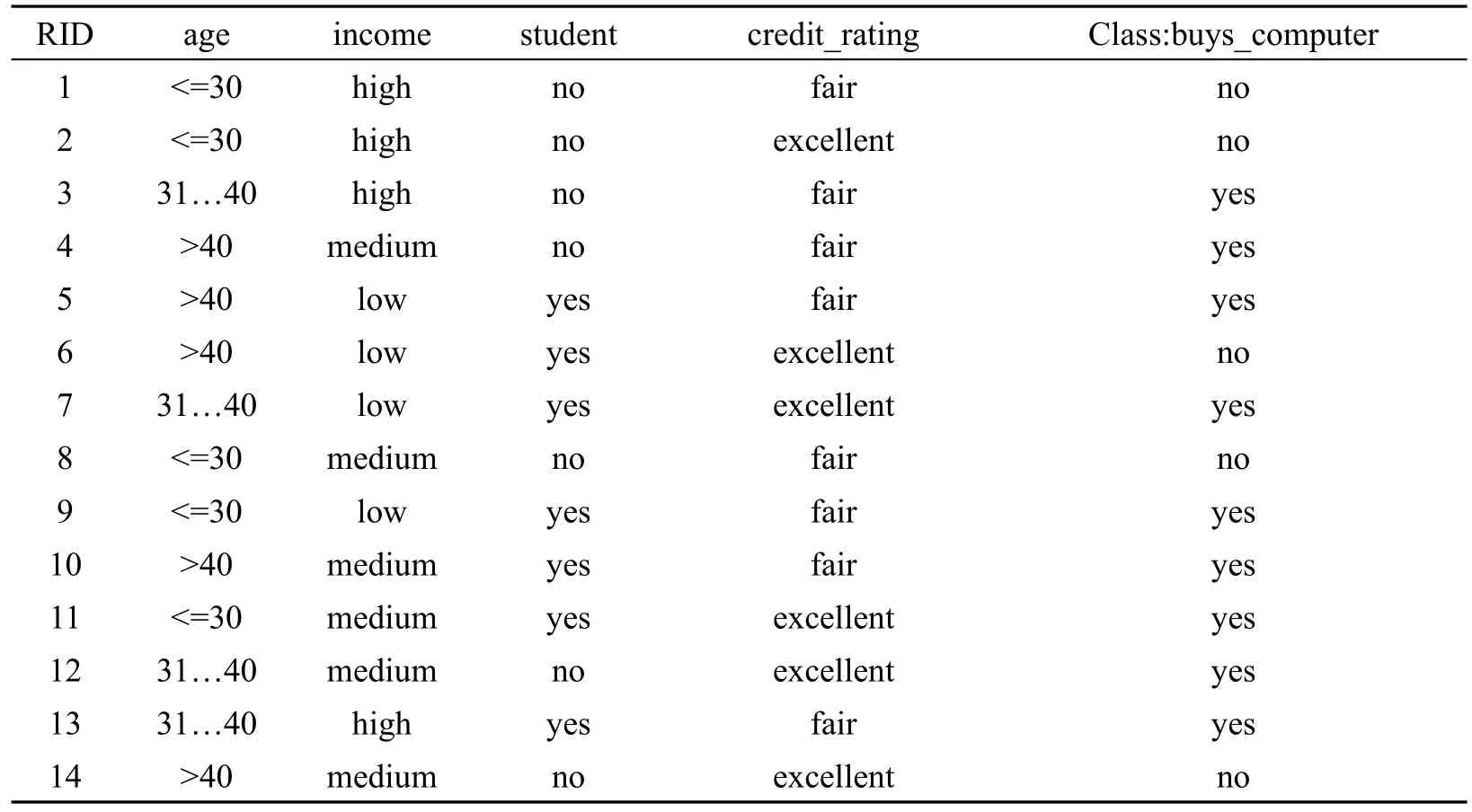
表2 给出了取自AllElectronics顾客数据库数据元组训练集（数据取自[Qui86]）

由于χ2(age)最大，所以由属性age划分样本。

由于上述各标准都选择属性age划分样本（可能是举例的样本集不合适的原因或样本量太小的原因，四种选择测试属性的标准都选择age属性作为分裂属性），所以据此划分样本得图1。

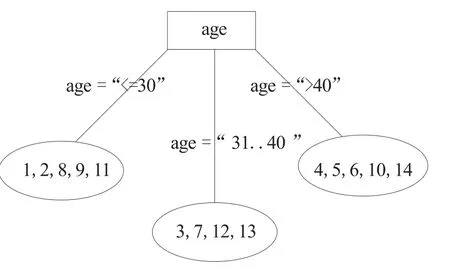
图1 根据age划分样本

图2 根据由样本集创建的决策树

同样对每个划分的样本集采用上述同样的算法构建决策树，最终得决策树如图2。

从上面过程可以看出，相比单独属性选择标准，通过多种属性选择标准来确定测试属性，是一种“多数表决”构建决策树。它适用于在给定数据集不知采用什么样的属性选择标准时或者使用每种属性选择标准都不理想时，这种情况的数据集在实际应用中可能最多，因此，多属性选择标准构建决策树的方法，具有更好和更广的适应性。同“专家会诊”的效果一样，通常情况下效果会很好，但也有例外的情况。这种方法计算量很大，构建决策树的效率低，但一旦建立好决策树，准确率要高，其准确率也有待用实际的数据集来验证。当然这种构建决策树的算法，是一种折中方法，实际应用也有通过测试集的测试，有较高的准确率后才用于以后的推测或估计。

3 结束语

本文介绍了构建决策树常用的四种测试属性选择标准：信息增益标准、信息增益率标准、Gini-Index标准和χ2统计标准。对于同一数据集，由于属性选择标准不同，构建的决策树可能不同；本文提出一种基于“多数表决”的思路，即采用“多数表决”选择测试属性构建决策树；设计并实现了相应的算法，给出了从一个具体的示例介绍基于多种属性选择标准“多数表决”构建决策树的过程。在给定数据集不知采用什么样的属性选择标准时或者使用任一一种属性选择标准都不理想时，采用“多数表决”构建决策树是一种合适的选择。

[1]张琳，陈燕，李桃迎，等.决策树分类算法研究[J]．计算机工程，2011，37（13）：66-67,70．

[2]Han J W,Kamber M.数据挖掘(概念与技术)[M]．北京：机械工业出版社，2006．

[3]Soman K P,Diwakar S,Ajay V.数据挖掘基础教程[M].北京：机械工业出版社，2011．

[4]L Breiman J H,Stone C J.Classification and regression trees[Z].1984.

[5]M.Mehta,R.Agrawal.SLIQ:A fast scalable classifier for data mining.int.conf.EDBT’96 28.

[6]谢妞妞，刘於勋.决策树属性选择标准的改进[J]．计算机工程与应用，2010，46（34）：115-118,139．

[7]喻金平，黄细妹，李康顺.基于一种新的属性选择标准的ID3改进算法[J].计算机应用研究，2012，29（8）：2895-2898,2908．

[8]孙淮宁，胡学钢.一种基于属性贡献度的决策树学习算法[J].合肥工业大学学报(自然科学版)，2009，32（8）：1137-1141．

[9]屈志毅，周海波.决策树算法的一种改进算法[J]．计算机应用，2008，28（z1）：141-143．

[10]邹永贵，范程华.基于属性重要度的ID3改进算法[J].计算机应用，2008，28（z1）：144-145,149．

[11]王小巍，蒋玉明.决策树ID3算法的分析与改进[J].计算机工程与设计，2011，32（9）：3069-3072,3076．

Majority voting optimization of decision tree with multiple attributes selection criteria

WANG Sen,ZHAO Fa-yong,CHEN Shu-guang
(School of Physics and Electronic Engineering,Fuyang Normal University,Fuyang Anhui236037,China)

The selection of test attributes is the key and core of constructing the decision tree.For the same data set,the decision trees constructed by different attribute selection criteria may vary greatly.Not to know which attribute selection criteria is good or not a standard suitable for handling data sets,this paper presents a solution,namely the majority voting optimization of decision tree with multiple attributes selection criteria algorithm,which uses the idea of“expert consultation”to construct the decision tree,with a wider adaptability and higher accuracy in the practical application.

attribute selection criteria;majority voting;decision tree

A

1004-4329（2017）01-061-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）01-061-05

2017-01-10

安徽省科技攻关项目（5101031114）资助。

王森（1973-）男，硕士，讲师，研究方向：软件工程、数据挖掘。